Jako ukázku použití GP uvedu symbolickou regresi. Regrese je statistická metoda používaná k předpovídání hodnoty nějaké proměnné, která je závislá na jedné nebo více nezávislých proměnných. [9] Symbolická regrese je jeden z možných způsobů, jak najít vhodnou regresní funkci pro zadaná data. Symbolická regrese není limitována určováním optimálních hodnot parametrů.

3 Ukázka použití genetického programování

Místo toho může být regresní funkce zkonstruována kombinací matematických výrazů, proměnných a konstant. V GP je cílová regresní funkce konstruována a upřesňována během evolučního procesu. Na začátku se v závislosti na velikosti populace a matematických výrazech, proměnných, respektive konstantách vytvoří počáteční populace, kde každý jedinec představuje jednu z možných regresních funkcí. Během evolučního procesu se vybírají nejvhodnější jedinci, kteří se vzájemně kříží, případně dochází k mutacím jedinců, dokud nenalezneme nejvhodnějšího jedince, tudíž nejvhodnější regresní funkci. [9]

Pro všechny níže uvedené příklady byly použity stejné hodnoty parametrů, které uvádím v tabulce (Tab.1).

Tab. 1.:Nastavení parametrů

Parametr	Hodnota
PopSize	700
Generations	500
Functions	{+, -, *, /, (-1)}
Terminals	{x, náhodné číslo z intervalu [-4,4]}
Method	HalfAndHalf
Depth	6
FrMutace	0.1
FrKrizeni	0.9
FrReprodukce	0

3.1 Příklady

V prvním příkladě byla hledána funkce

V prvním příkladě byla hledána funkce na intervalu 〈-3;3〉. Na obrázcích lze vidět zadanou funkci a porovnání hledané funkce a nejlepšího nalezeného řešení.

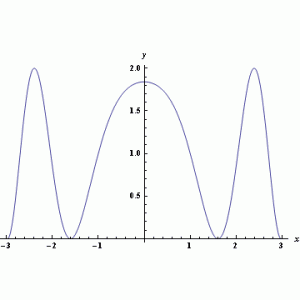
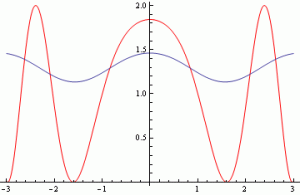
Obr. 13.:Hledaná funkce a její porovnání s nejlepším nalezeným řešením

Ve druhém příkladě byla hledána funkce

na intervalu 〈-3π;3π〉. Na obrázcích lze vidět zadanou funkci a porovnání hledané funkce a nejlepšího nalezeného řešení.

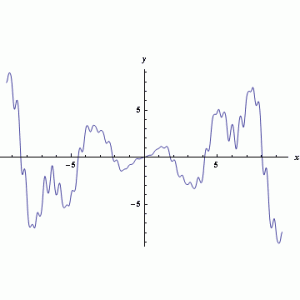
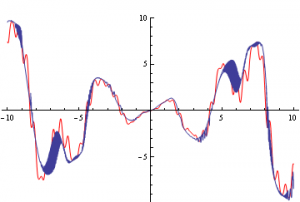
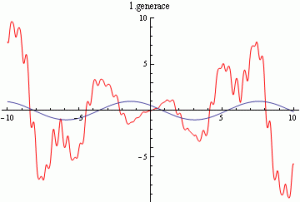
Obr. 14.: Hledaná funkce a její porovnání s nejlepším nalezeným řešením

V třetím příkladě byla hledána funkce

na intervalu 〈-4π;4π〉. Na obrázcích lze vidět zadanou funkci a porovnání hledané funkce a nejlepšího nalezeného řešení.

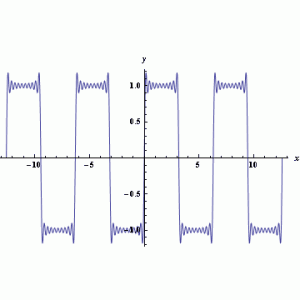
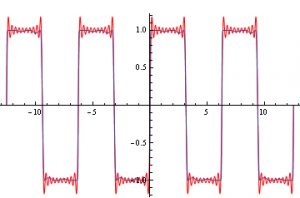
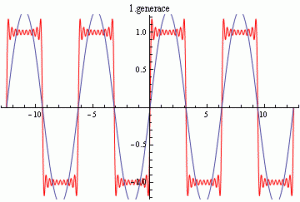
Obr. 15.: Hledaná funkce a její porovnání s nejlepším nalezeným řešením

V čtvrtém příkladě byla hledána funkce

na intervalu 〈-5;5〉. Na obrázcích lze vidět zadanou funkci a porovnání hledané funkce a nejlepšího nalezeného řešení.

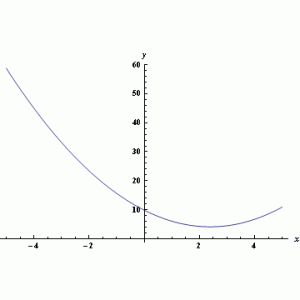
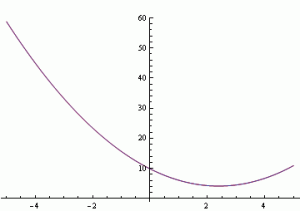
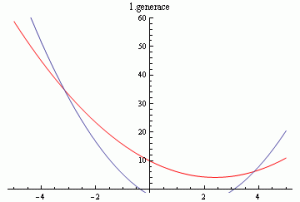
Obr. 16.: Hledaná funkce a její porovnání s nejlepším nalezeným řešením

V pátém příkladě byla hledána funkce

na intervalu 〈0;1〉. Na obrázcích lze vidět zadanou funkci a porovnání hledané funkce a nejlepšího nalezeného řešení.

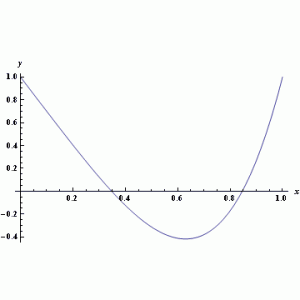
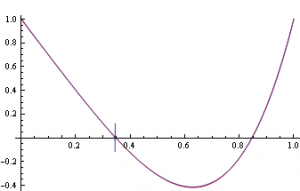
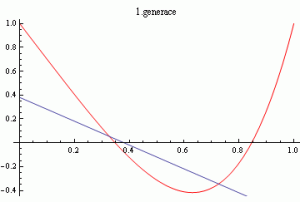
Obr. 17.: Hledaná funkce a její porovnání s nejlepším nalezeným řešením

V šestém příkladě byla hledána funkce

na intervalu 〈-1;1〉. Na obrázcích lze vidět zadanou funkci a porovnání hledané funkce a nejlepšího nalezeného řešení.

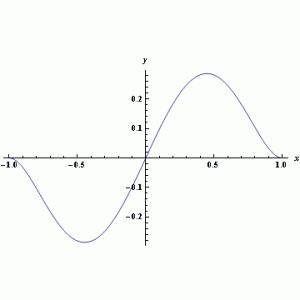
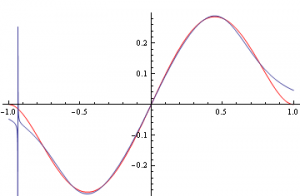
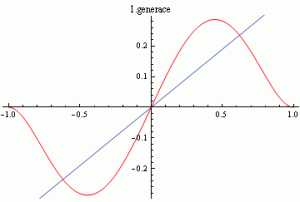
Obr. 18.: Hledaná funkce a její porovnání s nejlepším nalezeným řešením

Seznam použité literatury

1. O´REILLY, Una-May, et al. Genetic Programming Theory and Practice II. USA: Springer Science + Business Media, Inc., 2005. 337 s. ISBN 0-387-23253-2.
2. ZELINKA, Ivan, OPLATKOVÁ Zuzana, ŠENKEŘÍK Roman. Aplikace umělé inteligence: aneb vybrané statě z evolučních algoritmů. 1.vyd. Zlín: Univerzita Tomáše Bati ve Zlíně, 2010. 151 s. ISBN 978-80-7318-898-6.
3. KVASNIČKA, Vladimír, POSPÍCHAL, Jiří, TIŇO, Peter. Evolučné algoritmy. 1.vyd. Bratislava: Vydaveteľstvo STU, 2000. 223 s. ISBN 80-227-1377-5.
4. MAŘÍK Vladimír, et al. Umělá inteligence(4). 1.vyd., Praha: Academia 2003, ISBN 80-200-1044-0, Kapitola 5, Genetické programování a vybrané problémy evolučních výpočtů, s. 128-170.
5. HYNEK, Josef. Genetické algoritmy a genetické programování. 1.vyd. Praha: Grada Publishing, a.s., 2008. ISBN 978-80-247-2695-3, Kapitola 13, Genetické programování, s. 123-134.
6. KOZA, John R. Genetic Programming : On the Programming of Computers by Means of Natural Selection. Sixth. [s.l.] : Massachusetts Institute of Technology, 1998. 813 s. ISBN 0-262-11170-5.
7. POLI, Riccardo, LANGDON, William B., MCPHEE, Nicolas Freitag. A Field Guide to Genetic Programming. 1.vyd. [s.l.] : University of Essex, 2008. 250 s. ISBN 978-1-4092-0073-4.
8. KOZA, John R. Introduction to Genetic Programming: Tutorial. Přednáška v rámci GECCO 2007 London July 7-11, 2007
9. WEISE, Thomas. Global Optimization Algorithms : Theory and Application [online]. 2.vyd. [s.l.] : [s.n.], 2009, Version: 2009-06-26 [cit. 2010-05-14]. Dostupné z WWW : <http://www.it-weise.de/projects/book.pdf>.
10. SOULE, Terence. Removal Bias: A new cause of code growth in tree based evolutionary programming. In ICEC 98: IEEE International Conference on Evolutionary Computation 1998, IEEE Press, 1998, s. 781-786.
11. MCPHEE, N. A Schema Theory Analysis of the Evolution of Size in Genetic Programming with Linear Representations.