V článku je prezentované grafické používateľské prostredie, v ktorom sú implementované algoritmy prediktívneho riadenia založené na stavovom opise a na vstupno-výstupných regresných ARX a CARIMA modeloch dynamických systémov. Bližšie je rozoberaný spôsob algoritmizácie konkrétnych metód prediktívneho riadenia a programová realizácia uzavretého regulačného obvodu pre potreby simulácie riadenia lineárnych modelov dynamických systémov. V rámci článku je predložený aj ukážkový príklad simulácie prediktívneho riadenia modelu fyzikálneho systému Guľôčka na ploche.

1. Úvod

V tomto článku sa venujeme opisu grafického používateľského prostredia (ďalej len GUI –Graphical User Interface), ktoré sme vytvorili v prostredí Matlab za účelom simulácie riadenia lineárnych modelov dynamických systémov pomocou algoritmov prediktívneho riadenia. Podstatnú časť GUI tvoria implementované algoritmy prediktívneho riadenia, naprogramované ako samostatné funkcie, ktoré vypočítavajú veľkosť akčného zásahu na základe konkrétnych hodnôt vstupných parametrov. GUI sme naprogramovali s využitím nástroja guide, ktorý je súčasťou programového vybavenia Matlabu [1]. Pomocou tohto nástroja sme v GUI vytvorili potrebné grafické objekty a definovali im príslušné udalosti, teda činnosti, ktoré sa majú vykonať po ich aktivácii.

Na obr. 1 je hlavné okno GUI, ktoré sa zobrazí po spustení navrhnutej aplikácie. Môžeme ho rozdeliť na štyri časti. Ľavá horná časť slúži pre zadávanie lineárneho modelu dynamického systému v stavovom opise a v ľavej dolnej časti sa nachádzajú formuláre pre nastavenie parametrov algoritmov prediktívneho riadenia. V pravej hornej časti je možné pomocou tlačidla Step response zobraziť prechodovú charakteristiku zadaného modelu dynamického systému.

V grafe sa vykresľuje prechodová charakteristika s využitím funkcie step, ktorá je súčasťou Control System Toolboxu, ale aj pomocou nami naprogramovanej funkcie pre výpočet prechodovej charakteristiky preChar. Pomocou zaškrtávacích políčok pod grafom je možné zapnúť, resp. vypnúť mriežku v grafe pre os x a y. Pravá dolná časť hlavného okna slúži pre nastavenie parametrov simulácie, ako sú doba simulácie (Simulation time) v sekundách, šum (Noise), porucha (Disturbances). V tejto časti sa nachádza aj tlačidlo Simulate, ktorým sa spúšťa simulácia. Súčasťou okna je aj hlavné menu s položkami: System, Controller, Algorithm, Graphs, About.

V ďalšom bližšie popíšeme funkcionalitu GUI.

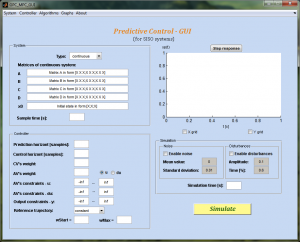
Obrázok 1: Hlavné okno grafického používateľského prostredia

2. Definovanie modelu dynamického systému v GUI

V rámci GUI je možné zadávať spojitý, resp. diskrétny stavový opis lineárneho modelu SISO dynamického systému v tvare

(1)

kde A, resp. A_d je matica dynamiky s rozmermi nx_xnx, b, resp. b_d je stĺpcový vektor vstupu s dĺžkou nx, c^T je riadkový vektor výstupu s dĺžkou nx, d je koeficient priamej väzby medzi vstupom a výstupom, x(t), resp. x(k) je stĺpcový vektor stavových veličín s dĺžkou nx, u(t), resp. u(k) je hodnota vstupu, y(t), resp. y(k) je hodnota výstupu, pričom premenná nx vyjadruje počet stavov dynamického systému. Stavový opis (1) je možné získať linearizáciou nelineárnych diferenciálnych rovníc

(2)

popisujúcich dynamiku konkrétneho fyzikálneho systému, kde t je čas, f a g sú vektorové, väčšinou nelineárne funkcie. Musíme podotknúť, že aktuálna verzia GUI je obmedzená na systémy s jedným vstupom a jedným výstupom. Rozšírenie na viacparametrové systémy je obsiahnuté v ďalšej verzii GUI, ktorá je momentálne vo vývoji.

Na základe voľby používateľ zadáva spojitý alebo diskrétny stavový opis lineárneho modelu dynamického systému, ktorý bude použitý ako riadený systém. Zároveň sa zadaný model použije pri predikcii v rámci vybraných algoritmov prediktívneho riadenia. Je potrebné poznamenať, že v prípade zadávania diskrétneho stavového opisu musí byť definovaná perióda vzorkovania v korešpondencii s maticami stavového opisu. V prípade zadávania spojitého stavového opisu sa daná perióda vzorkovania použije pri diskretizácii modelu. GUI umožňuje prostredníctvom položky System v hlavnom menu ukladať, prípadne načítavať skôr uložený lineárny model dynamického systému zo súboru.

3. Algoritmy prediktívneho riadenia implementované v GUI

Algoritmy prediktívneho riadenia, ktoré sú implementované v GUI patria k optimalizačným algoritmom a vo všeobecnosti minimalizujú funkcionál v tvare

(3)

kde u(k) je akčný zásah, ŷ(k) predikovaná hodnota regulovanej veličiny a w(k) referenčná trajektória. Hodnoty N₁ až N_p udávajú horizont predikcie (predikčný horizont), na ktorom sa vypočítava optimálna postupnosť hodnôt akčného zásahu u(k). Kladná hodnota N_u predstavuje riadiaci horizont, pričom platí . Ak sa pri metódach prediktívneho riadenia používa redukcia stupňov voľnosti akčného zásahu, platí . V niektorých prípadoch sa vo funkcionáli (3) namiesto akčného zásahu u(k) používa zmena akčného zásahu Δu(k), čím riadenie získava integračný charakter [2]. Dôležitým faktom v prípade metód prediktívneho riadenia je nutnosť poznať referenčnú trajektóriu w(k) na celej dĺžke predikčného horizontu.

Algoritmy prediktívneho riadenia, ktoré sme implementovali do GUI môžeme rozdeliť do dvoch kategórií: algoritmy založené na stavovom opise – stavové MPC (Model Predictive Control), pre ktoré je riadiaca schéma zobrazená na obr. 2 a algoritmy vychádzajúce z prenosových funkcií – GPC (Generalized Predictive Control), ktorých použitie znázorňuje riadiaca schéma na obr. 3. V rámci každej kategórie sme naprogramovali dva typy algoritmov:

A. stavové MPC algoritmy

A1. stavový MPC algoritmus s prediktorom v tvare

(4)

(v GUI označený ako MPC v.1, detailne rozobraný v [2], prípadne [9]),

A2. stavový MPC algoritmus s prediktorom v tvare

(5)

(v GUI označený ako MPC v.2, detailne rozobraný v [3], prípadne [9]),

kde x(k) je vektor aktuálneho stavu, u, resp. ∆u je postupnosť hodnôt, resp. zmien akčného zásahu. Za predpokladu, že v stavovom opise modelu dynamického systému (1) je koeficient priamej väzby d=0, má vektor predikovaných hodnôt výstupu , vektor postupnosti akčného zásahu u, matica voľnej odozvy V a matice vynútenej odozvy dynamického systému G, G₁, G₂ tvar

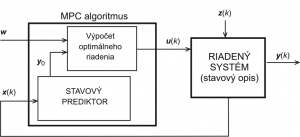
Obrázok 2: Riadiaca štruktúra so stavovým MPC riadiacim algoritmom

B. GPC algoritmy

B1. GPC algoritmus vychádzajúci z ARX modelu dynamického systému

(6)

pri vyjadrení prediktora v tvare

(7)

(v GUI označený ako GPC ARX, detailne rozobraný v [4], prípadne [9]),

B2. GPC algoritmus vychádzajúci z CARIMA modelu dynamického systému

(8)

pri vyjadrení prediktora v tvare

(9)

kde

• B_z(z^-1), resp. A_z(z^-1) sú polynómy čitateľa, resp. menovateľa rádu m, resp. n s koeficientmi b_i, resp. a_i, C_z(z^-1) je polynóm,
• u(k) je vstup, y(k) je výstup dynamického systému a ξ(k) je chyba výstupu systému, resp. podľa [4] šum merania výstupu,
• predstavuje integrátor [5].

Vo vzťahoch (7) a (9) je y₀ vektor predikcie hodnôt voľnej odozvy systému a výrazy predstavujú vynútenú odozvu systému, pričom matice G₃ a G₄ je možné určiť na základe vzťahov uvedených v [9]. Po dosadení prediktorov (4), (5), (7) a (9) do funkcionálu (3) v maticovom tvare

(10)

môžeme odvodiť kvadratickú formu (zvlášť pre príslušný algoritmus), ktorú je potrebné minimalizovať podľa u, resp. ∆u:

(11)

Bližší postup a odvodenie je uvedené v [1], [3], [4], [5] a [9]. Akčný zásah je na základe podmienky o minimalizácii funkcionálu

(12)

daný rovnicou

(13)

kde tvar matice H a riadkového vektora g^T závisí od použitého algoritmu riadenia, pričom ich konkrétny tvar pre jednotlivé algoritmy je uvedený v [9].

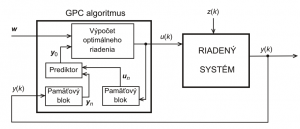
Obrázok 3: Riadiaca štruktúra s GPC riadiacim algoritmom

Navrhnuté GUI umožňuje definovať model dynamického systému iba vo forme stavového opisu. Z tohto dôvodu v prípade GPC riadiacich algoritmov dochádza pred akýmkoľvek ďalším výpočtom k transformácii matíc stavového opisu na prenosovú funkciu, ktorá predstavuje vstupno-výstupný opis modelov dynamických systémov.

Výhodou algoritmov prediktívneho riadenia je možnosť zakomponovať rôzne obmedzenia (akčného zásahu, zmeny akčného zásahu, výstupu) do výpočtu optimálneho riadenia. Tento výpočet sme realizovali pomocou kvadratického programovania, konkrétne pomocou funkcie quadprog v toolboxe Matlabu Optimization Toolbox, ktorá vypočítava vektor optimálnych hodnôt akčného zásahu minimalizáciou vzťahu (11) pri zohľadnení obmedzení . Základná syntax použitia tejto funkcie na výpočet vektora optimálnych hodnôt u, resp. ∆u je

(14)

kde maticu Aobm a vektor bobm je potrebné zostaviť podľa požadovaných obmedzení, pričom ich konkrétny tvar pre jednotlivé algoritmy je uvedený v [9]. Vývojový diagram, na základe ktorého sme realizovali implementáciu stavových MPC algoritmov ako funkcií jazyka Matlab je na obr. 4. Pre implementáciu GPC algoritmov je potrebné niektoré kroky špecificky upraviť, no celkový postup zostáva zachovaný.

Na určenie hodnoty akčného zásahu sme používali výpočet s pohyblivým horizontom [2], teda z optimálnej postupnosti akčného zásahu

vypočítanej na základe vzťahu (13) alebo (14) – v každom kroku k predstavuje hodnotu výstupného parametra funkcie každého algoritmu iba prvý člen u_opt(k). Algoritmus výpočtu optimálnej postupnosti akčného zásahu uopt s využitím prediktívneho riadenia s pohyblivým horizontom môžeme vyjadriť v týchto krokoch:

1. určenie referenčnej trajektórie na dĺžke horizontu predikcie w,
2. zistenie skutočného stavu x(k), resp. výstupu y(k) systému v danom kroku,
3. predikcia správania sa systému na horizonte predikcie na základe skutočných hodnôt akčného zásahu u_opt(k) a stavu x(k) v predošlých krokoch, tzv. voľná odozva systému,
4. výpočet postupnosti akčného zásahu u_opt minimalizáciou funkcionálu J (3) pri známych parametroch N₁, N_p, N_u, Q(i) a R(i),
5. použitie uopt(k) na vstupe systému a späť na krok č. 1.

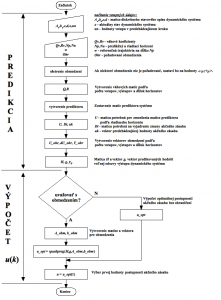
Obrázok 4: Vývojový diagram algoritmizácie stavových MPC algoritmov

Nastaviteľnými parametrami pre rozoberané riadiace algoritmy sú predikčný horizont N_p, riadiaci horizont N_u, váhové koeficienty Q(i) a R(i), prípadne požadované ohraničenia na akčný zásah, resp. výstup dynamického systému. Hodnotu parametra N₁ sme v našom prípade nastavili na 1.

Hodnoty uvedených parametrov môže používateľ nastavovať a meniť v ľavej dolnej časti GUI. V tejto časti je potrebné určiť aj typ, počiatočnú a maximálnu hodnotu referenčnej trajektórie, ktorá bude na základe týchto údajov vygenerovaná v rámci simulácie. Rovnako, ako v prípade modelu dynamického systému, aj v prípade nastavení parametrov riadiacich algoritmov, je možné tieto údaje ukladať a spätne načítavať zo súboru prostredníctvom položky Controller v hlavnom menu.

4. Simulácia algoritmov prediktívneho riadenia a zobrazovanie výsledkov v GUI

V procese simulácie prediktívneho riadenia je možné použiť jeden stavový MPC a jeden GPC algoritmus naraz z dôvodu vzájomného porovnania ich účinkov v riadiacej štruktúre podľa obr. 2 a obr. 3. Výber algoritmov použitých v simulácii riadenia je potrebné vykonať prostredníctvom položky Algorithms v hlavnom menu, ako je to znázornené na obr. 5 vľavo.

Nastavenie doby simulácie (Simulation time) v sekundách, strednej hodnoty (Mean value) a smerodajnej odchýlky šumu (Standard deviation), ako aj amplitúdu (Amplitude) a čas pôsobenia poruchy (Time) v percentuálnom vyjadrení z doby simulácie je možné uskutočniť v pravej dolnej časti GUI. V prípade požiadavky na zašumenie riadeného procesu je prostredníctvom generátora šumu vygenerovaný šum s údajmi definovanými používateľom a pripočítaný k stavom, resp. výstupu systému. Porucha je realizovaná ako skokový prírastok a neskôr úbytok od akčného zásahu v čase určenom používateľom.

Po zadefinovaní lineárneho modelu dynamického systému, výbere a nastavení parametrov riadiacich algoritmov, referenčnej trajektórie a prípadnom nastavení parametrov šumu a poruchy je simuláciu riadenia možné spustiť prostredníctvom tlačidla Simulate. Priebeh simulácie riadenia je indikovaný slovom Simulating… pod stlačeným tlačidlom, pričom po úspešne uskutočnenej simulácii sa na tomto mieste zobrazí informácia o dĺžke trvania danej simulácie. Algoritmus, pomocou ktorého sme simulovali riadenie modelov dynamických systémov na základe riadiacich štruktúr uvedených na obr. 2 a obr. 3, má niekoľko krokov:

1. Načítanie vstupných údajov
   • matice diskrétneho stavového opisu dynamického systému, v prípade GPC algoritmov transformácia na čitateľ a menovateľ diskrétnej prenosovej funkcie,
   • perióda vzorkovania T_vz , doba regulácie (simulácie) T_sim,
   • vektor referenčnej trajektórie w,
   • nastavenie šumu a poruchovej veličiny z.
2. Inicializácia údajov
   • nastavenie počiatočného výstupu y(0), resp. stavu x(0) systému,
   • nulovanie hodnôt, ktoré vo vstupno-výstupnom opise dynamického systému predstavujú hodnoty v zápornom čase,
   • určenie počtu vzoriek: , kde T_sim je doba simulácie
     a T_vz je perióda vzorkovania,
   • nastavenie počítadla vzoriek: , kde n je rád systému.
3. Výpočet regulačnej odchýlky e(k)=w(k)-y(k).
4. Výpočet akčného zásahu u(k) podľa konkrétneho vzťahu pre použitý typ riadenia + prípadná saturácia akčného zásahu.
5. Pripočítanie poruchovej veličiny k akčnému zásahu (ak je zadaná).
6. Výpočet nového výstupu y(k) s využitím vypočítaného akčného zásahu u(k) na základe:
   • diskrétnej prenosovej funkcie (pre GPC),
   • matíc stavového opisu (pre stavové MPC).
7. Pripočítanie šumu k stavom, resp. výstupu (ak chceme simulovať riadenie so šumom).
8. Nastavenie stavu, resp. výstupu lineárneho modelu dynamického systému podľa stavu, resp. výstupu riadeného systému.
9. 
10. Ak , potom skok na bod 3.
11. Odstránenie vzoriek v zápornom čase (ak je to potrebné).
12. Grafický výstup výsledkov simulácie.

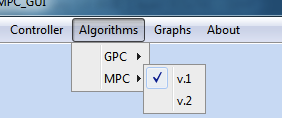
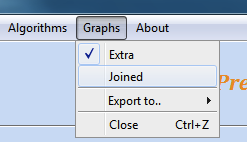
Obrázok 5: Ponuka položiek Algorithms a Graphs v hlavnom menu GUI

Akonáhle je simulácia úspešne skončená, zobrazia sa jednotlivé časové priebehy akčného zásahu u(k), referenčnej trajektórie w(k) a výstupu dynamického systému y(k) v príslušných grafoch podľa voľby používateľa v položke Graphs v hlavnom menu (obr. 5 vpravo). V aktuálnej verzii GUI je možné výsledky zobraziť nasledovne:

• Extra – výsledky simulácie sa zobrazia v osobitnom grafe pre vybraný MPC algoritmus a osobitnom grafe pre vybraný GPC algoritmus, pričom sú zobrazené výsledky, kde boli pri výpočte zohľadnené aj požadované ohraničenia na akčný zásah, prípadne výstup dynamického systému a taktiež výsledky bez týchto ohraničení,
• Joined – výsledky simulácie pre MPC a GPC algoritmus sa zobrazia spolu v jednom grafe, pričom zobrazené sú iba výsledky, kde boli vo výpočte zohľadnené požadované ohraničenia na akčný zásah, prípadne výstup dynamického systému.

GUI sme naprogramovali tak, aby výsledky simulácie pre používateľom zadaný typ váženia hodnoty u alebo zmeny akčného zásahu ∆u vo funkcionáli (10) boli zobrazené v osobitných grafoch. Je to tak navrhnuté z tohto dôvodu, aby bolo možné zobraziť výsledky simulácie pri oboch typoch váženia naraz, avšak nie v jednom grafe. Na základe vyššie uvedených spôsobov algoritmizácie GUI je možné uskutočniť porovnania výsledkov:

1. vybraného algoritmu, kde boli, resp. neboli zohľadnené ohraničenia v jednom grafe,
2. vybraného stavového MPC a GPC algoritmu v jednom grafe (iba s ohraničeniami),
3. vybraného algoritmu, kde bola vo funkcionáli vážená hodnota u a ∆u (osobitne).

V položke Graphs v hlavnom menu je aj voľba Export to.. → .mat file, po ktorej zaškrtnutí je používateľovi po úspešnej simulácii ponúknutá možnosť uloženia časových priebehov vo forme .mat súboru.
Položka Graphs/Close v hlavnom menu uzatvára všetky otvorené okná s časovými priebehmi, čo zrýchľuje prácu s výsledkami simulácie.

5. Ukážkový príklad simulácie riadenia systému Guľôčka na ploche

V tejto časti uvádzame ukážkový príklad pre prácu s GUI. Ako riadený systém sme zvolili lineárny model fyzikálneho systému Guľôčka na ploche, ktorý pozostáva z plochy nakláňajúcej sa okolo svojej stredovej osi tak, že sklon plochy môže byť ovládaný krokovými motormi v dvoch smeroch (uhly α a β) a guľôčky, ktorá sa pohybuje po ploche (obr. 6). Poloha guľôčky (súradnice y_x a y_y) je snímaná prostredníctvom kamery, ktorej obraz je spracovávaný v počítači, kde sa pomocou algoritmov riadenia vypočíta a následne vyšle vhodné napätie späť na krokové motory (u_α a u_β) [6].

Riadením reálneho fyzikálneho systému Guľôčka na ploche pomocou číslicových PSD algoritmov sme sa bližšie zaoberali v rámci bakalárskeho štúdia, čoho výsledkom je bakalárska práca [7] a tiež článok [8] na medzinárodnej konferencii Process Control 2009 (http://www.kirp.chtf.stuba.sk/pc09/data/abstracts/038.html).

V rámci inžinierskeho a doktorandského štúdia je tento systém využívaný pri overovaní algoritmov moderných metód riadenia, kde patrí aj prediktívne riadenie rozoberané v tomto článku.

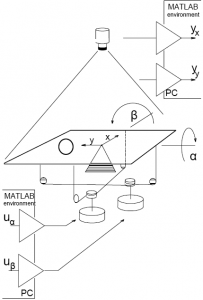
Obrázok 6: Schéma fyzikálneho systému Guľôčka na ploche

Postup práce s GUI pri simulačnom riadení lineárneho modelu Guľôčka na ploche:

1. Načítanie lineárneho modelu zo súboru – Pomocou klávesovej skratky CTRL+L zobrazíme dialógové okno. Z podadresára examples vyberieme súbor BP_system. V hlavnom okne sa automaticky vyplní časť pre zadávanie modelu dynamického systému príslušnými maticami, ktoré vznikli linearizáciou nelineárneho modelu.
2. Nastavenie parametrov algoritmu prediktívneho riadenia – Parametre algoritmu prediktívneho riadenia nastavíme podľa týchto hodnôt:
   • Prediction horizon [samples] = 10;
   • Control horizon [samples] = 2;
   • CV’s weight = 100;
   • AV’s weight = 0,01;
   • AV’s constraint – u=<-1 ; 1> zaškrtneme u;
   • AV’s constraint – du = <-inf ; inf> (neobmedzene);
   • Output constraint – y = <-inf ; inf> (neobmedzene);
   • Reference trajectory = stairs up & down (schody hore a dole),
   • wStart = -0,15;
   • wMax = 0,12.
3. Výber požadovaných algoritmov – V hlavnom menu vyberieme položku Algorithms → GPC → CARIMA a Algorithms → MPC → v.1. (Sú to zároveň východzie nastavenia).
4. Výber požadovaných algoritmov – V hlavnom menu vyberieme položku Algorithms → GPC → CARIMA a Algorithms → MPC → v.1. (Sú to zároveň východzie nastavenia).
5. 5. Nastavenie šumu, poruchy a doby simulácie – Povolíme šum a poruchu a ich hodnoty nastavíme takto:
   • Mean value = 0;
   • Standard deviation = 0,001;
   • Amplitude = 0,2;
   • Time [%] = 0,5;
   • Simulation time [s] = 50;
6. Simulácia a zobrazenie výsledkov s ich uložením. – Po stlačení tlačidla Simulate sa zobrazí jedno okno rozdelené na dve časti podľa obr. 7, porovnali sme teda stavový MPC a GPC algoritmus pri zašumenom riadenom systéme. Získané časové priebehy sú zobrazené na nasledujúcom obrázku.

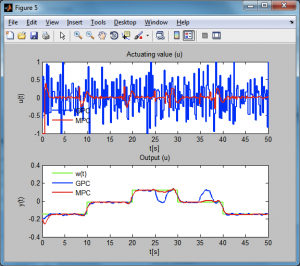
Obrázok 7: Výsledky simulácie prediktívneho riadenia lineárneho modelu systému Guľôčka na ploche pomocou GUI (zobrazenie výsledkov v jednom grafe)

Avšak, keďže sme vybrali možnosť exportovať výsledky do súboru, objavilo sa aj dialógové okno, v ktorom môžeme zadať názov súboru, do ktorého budú uložené výsledky simulácie riadenia.

V prípade požiadavky zobrazenia výsledkov v osobitných grafoch, teda zmenou 4. kroku na Graphs → Extra získame nasledujúce dva obrázky. V tomto prípade sú v grafoch zobrazené aj časové priebehy získané prediktívnym riadením bez rešpektovania daných obmedzení. Je dôležité podotknúť, že obr. 7 a obr. 8 nezobrazujú úplne rovnaké výsledky. Výsledky na obr. 8 boli získané opätovným spustením simulácie, pri ktorej bol vygenerovaný iný šum. V prípade simulácie bez šumu by výsledky na obr. 7 a obr. 8 boli identické.

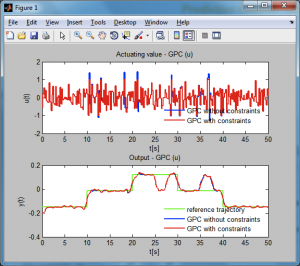
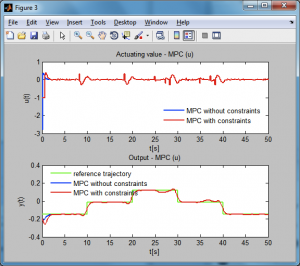
Obrázok 8: Výsledky simulácie prediktívneho riadenia lineárneho modelu systému Guľôčka na ploche pomocou GUI (zobrazenie výsledkov v osobitných grafoch)

6. Záver

V článku sme prezentovali prácu s vytvoreným grafickým používateľským prostredím pre simulačné riadenie modelov dynamických systémov pomocou algoritmov prediktívneho riadenia. Toto grafické používateľské prostredie môže byť plnohodnotne využité pri porovnávaní výsledkov riadenia medzi rôznymi navrhnutými algoritmami prediktívneho riadenia, ako aj na analýzu vplyvu zakomponovania požadovaných ohraničení do výpočtu optimálnej postupnosti akčného zásahu.

Konkrétne využitie tohto prostredia bude vo výučbe predmetu Riadenia a umelá inteligencia, ktorý sa vyučuje na inžinierskom stupni štúdia na Katedre kybernetiky a umelej inteligencie FEI TU v Košiciach. V rámci tohto predmetu bude slúžiť ako pomôcka pre študentov a bude im poskytovať nástroj pre kontrolu správnosti výsledkov, ktoré získali na základe nimi naprogramovaných algoritmov prediktívneho riadenia.

Prezentované grafické používateľské prostredie je naďalej vo vývoji, postupne ho rozširujeme o nové funkcionality. Ďalšiu verziu dopĺňame o algoritmy prediktívneho riadenia s využitím nástrojov iných toolboxov, ktoré sa špecializujú na prediktívne riadenie a rozširujeme už existujúce riadiace algoritmy. Okrem toho rozširujeme množinu možných modelov dynamických systémov, konkrétne o mnohorozmerné modely a tiež nelineárne modely, ktoré sú matematicky vyjadrené vo forme nelineárnych diferenciálnych rovníc. Vytvárame prepracovanejší nástroj na generovanie referenčnej trajektórie a celkovo pridávame do GUI aj niekoľko menších vylepšení.

Poďakovanie

Tento článok bol vytvorený realizáciou vedeckého projektu Vega č. 1/0286/11 Grantovej agentúry SR pod názvom Dynamické hybridné architektúry v multiagentových sieťových riadiacich systémoch (50%) a projektu Rozvoj Centra informačných a komunikačných technológií pre znalostné systémy (ITMS kód: 26220120030) na základe podpory operačného programu Výskum a vývoj financovaného z Európskeho fondu regionálneho rozvoja (50%).

Použitá literatúra

1. THE MATHWORKS: Creating Graphical User Interfaces (User’s guide). Dostupné na internete: http://www.mathworks.com/help/pdf_doc/matlab/buildgui.pdf
2. ROUBAL, Jiří: Prediktívni regulátor (Příklady ze cvičení – Moderní teorie řízení). Dostupné na internete: http://support.dce.felk.cvut.cz/pub/roubalj/teaching/MTR/seminars/MTR_cv8_mpc.pdf.
3. BELDA, Květoslav – BÖHM, Josef – VALÁŠEK, Michael: Model-Based Control for Parallel Robot Kinematics. Proceeding of the 3rd International Congress on Mechatronics. MECH2K4. (CD ROM). CTU in Prague, FM, Prague 2004, 15 pp.
4. BELDA, Květoslav – BÖHM, Josef.: Adaptive Predictive Control for Simple Mechatronic Systems. Proceedings of the WSEAS CSCC & EE International Conferences. WSEAS Press, Athens, Greece 2006, pp. 307-312.
5. FIKAR, Miroslav: Predictive Control – An Introduction. Bratislava: Slovenská technická univerzita – FCHPT, 1999.
6. Humusoft: CE151 Ball & Plate model, Educational Manual, 1996 – 2004.
7. JAJČIŠIN, Štefan: Modelovanie a riadenie dynamických systémov v prostredí Matlab/Simulink. Bakalárska práca. Košice: TU-FEI, 2008.
8. JADLOVSKÁ, Anna – JAJČIŠIN, Štefan – LONŠČÁK, Richard: Modelling and PID Control Design of Nonlinear Educational Model Ball & Plate. Košice: TU-FEI. Medzinárodná konferencia Process Control, 2009.
9. JAJČIŠIN, Štefan: Aplikácia moderných metód v riadení nelineárnych výukových modelov. Diplomová práca. Košice: TU-FEI, 2010.

---

Spoluautorom článku je Anna Jadlovská, Katedra kybernetiky a umelej inteligencie, FEI TU v Košiciach, Slovenská republika