Inferenčná miera nerovnomernosti

22. Jún, 2011, Autor článku: Ladovský Tomáš, Informačné technológie
Ročník 4, číslo 6 Pridať príspevok

Miera nerovnomernosti ( $\mathcal{MN}$ ) plní dôležitú úlohu kritériálnej funkcie pri tvorbe rovnomerných rozvrhov ( $\mathcal{RR}$ ). Špeciálne typy rozvrhy vieme matematicky formulovať pomocou maticového zápisu, v ktorom prvok predstavuje aktivity, stĺpec predstavuje časový horizont, riadok predstavuje postupnosť aktivít pridelených zdroju na spracovanie a jednotlivé riadkové súčty predstavujú kumulované výkony aktivít pridelené k zdrojom.

Tieto riadkové súčty predstavujú vstupný argument $\mathcal{MN}$ . Čim je $\mathcal{MN}$ menšia, tým je rozvrh viac rovnomerný. Ak sú rozvrhované aktivity reprezentované pomocou neistých čísel, potom je tvorca rozvrhu vedený k výskumu a vývoji nových tvarov $\mathcal{MN}$ , ktoré sú schopné prijať a vyhodnotiť vstupný argument neistých riadkových súčtov. Veľkosti aktivít modelujeme v tomto prípade pomocou fuzzy čísel. Vzhľadom na tento predpoklad sme navrhli inferenčnú mieru nerovnomernosti za pomoci teórie fuzzy inferenčných systémov.

1. Úvod

Rovnomerné rozvrhy ( $\mathcal{RR}$ ) získavame pomocou procesu rozhodovania optimalizáciou kritériálnej funkcie, ktorú nazývame miera nerovnomernosti. Vzhľadom na Grahamovú klasifikáciu môžeme problematiku tvorby rovnomerných rozvrhov rozdeliť na štandardné a neštandardné rovnomerné rozvrhy. Medzi štandardné rozvrhy patrí rozvrhovanie úloh špecifickým paralelným strojom a rozvrhovanie úloh v sériovej/zákazkovej/otvorenej výrobe. Medzi neštandardné rovnomerné rozvrhy zaraďujeme problematiku rozpisovania služieb vodičom autobusov, letcom, letuškám, sestričkám v nemocnici a veľa iných.

Veľké množstvo neštandardných rozvrhov vieme matematicky formulovať pomocou matice, ktorej stĺpec predstavuje časový horizont, riadok predstavuje postupnosť pridelených aktivít danému zdroju a prvky predstavujú plánované výkony aktivít. Riadkové súčty matice predstavujú kumulované výkony zdrojov, na základe ktorých vyhodnocujeme mieru nerovnomernosti a ktoré sa v práci snažíme zrovnomerniť. Túto rovnomernosť rozvrhu vieme získať permutovaním prvkov v stĺpcoch tak, aby čo najlepšie optimalizovali mieru nerovnomernosti, ktorá môže nadobúdať nasledujúce tvary

$f_{dev}(x_1, \dots, x_m)=\frac{1}{m}\sum_{i=1}^{m}\frac{|x_i-\bar{x}|}{\bar{x}}$

(1)

$f_{ssqr}(x_1, \dots, x_m)=\frac{1}{m}\sum_{i=1}^{m} (x_i - \bar{x})^2$

(2)

Za predpokladu, že vytvárame rozvrh v doprave, môžu jednotlivé premenné $x_1$ až $x_m$ predstavovať plánované pracovné zaťaženia m vodičov a $\bar{x}$ je ideálnym pracovným zaťažením vodičov, v tomto prípade priemernou hodnotou, ktorú spočítame ako

$\bar{x} = \frac{1}{m} \sum_{i=1}^{m} x_i$

Rozvrhy, ktoré vznikli optimalizáciou miery nerovnomernosti, nazývame rovnomernými rozvrhmi. Vzhľadom na známu Grahamovu [1] klasifikáciu ide o neštandardný typ rozvrhov.

Táto maticová formulácia neštandardných rozvrhov je vďaka predošlému výskumu u nás a v zahraničí známa pod menom problém rovnomernosti riadkových súčtov stĺpcovo permutovanej matice, a ktorá je v anglosaskej literatúre známa pod menom “The Matrix Permutation Problem”, $\mathcal{MPP}$ [3].

S neistotou sa v rovnomerných rozvrhoch stretávame napr. pri plánovaní budúcej realizácie výkonu aktivity. Takéto rozvrhy nazývame $\mathcal{RR}$ pri neistote. Z pohľadu $\mathcal{MPP}$ problematiky to znamená, že prvky matice sú neisté čísla. Pod neistými číslami si predstavujeme reálne intervaly, fuzzy čísla a náhodné premenné. V nasledujúcom texte sa zameriame iba na fuzzy čísla.

2. Súčasný stav

Rovnomerné rozvrhy môžeme zovšeobecniť a matematicky formulovať ako kombinatorický problém rovnomernosti riadkových súčtov stĺpcovo permutovanej matice. Vhodným preusporiadaním stĺpcov matice môžeme docieliť väčšiu rovnomernosť riadkových súčtov matice/rozvrhu.

Definícia 1 (Matrix permutation problem [2])

Nech $\mathcal M=\{1,2,\dots,m\}$ a $\mathcal N=\{1,2,\dots,n\}$ sú konečné neprázdne množiny a nech $\mathbb A=(a_{ij})\in\mathfrak R^{m\times n}$ je reálna matica rozmeru $m\times n$ . Hľadá sa taká matica permutácií $\Psi = (\psi_j)_{j\in N}$ stĺpcov matice $\mathbb A$ pre ktorú platí:

$\min_{\psi\in\Pi(\mathcal M)}\Big\{ f(s^{\psi}_1,s^{\psi}_2,\dots,s^{\psi}_m) \:|\: s^{\psi}_i=\sum_{j\in\mathcal N} a_{\psi_{ij},j},\forall i\in\mathcal M$

$\psi_j = (\psi_{1j},\psi_{2j}\dots,\psi_{mj}),\forall j\in\mathcal N \Big\}$

kde f je nejaká miera nerovnomernosti vektora reálnych čísel, $s^{\psi}_i$ je i-ty riadkový súčet matice ${\mathrm A}^\psi$ a $\Pi(\mathcal M)$ je množina všetkých permutácií množiny $\mathcal M$ . Riešením takto formulovanej úlohy $\mathcal{MPP}$ je matica ${\mathbb A}^\psi = (a_{\psi_{ij},j})$

Problematiku ${\mathcal MPP}$ vieme riešiť pomocou heuristických metód. Za zmienku stojí veľmi rýchla a kvalitná stochastická dekompozičná metóda ${\mathcal SDM}$ [2] a metóda deň-po-dni [4] (stĺpec-po-stĺpci) ${\mathcal DBD}$ . Stochastická dekompozičná metóda pracuje na princípe rozkladu problému na dvojstĺpcovú variantu ${\mathcal MPP}$ problém, jej riešením a následným spätným vytváraním všeobecnej matice. Metóda stĺpec-po-stĺpci najskôr pridelí aktivity riadkom pre prvý stĺpec, potom pre druhý a takto pokračuje až po posledný stĺpec. Toto prideľovanie uskutočňujeme s ohľadom na mieru nerovnomernosti.

Veľmi zaujímavá varianta problému ${\mathcal MPP}$ vzniká pri dvojstĺpcovej matici, tzv. n=2, ktorú označujeme ${\mathcal MPP2c}$ . Túto variantu vieme riešiť exaktne v polynomiálnom čase pomocou \textit{priraďovacej úlohy} bivalentného lineárneho programovania, kde maticu priradení $X = (x_{ij})$ definujeme ako

$x_{ij} = \left\{ \begin{array}{ccc} 1 & \text{potom} & \psi_{i1} = i, \psi_{i2} = j \\ 0 & \text{nic nerob} & \end{array} \right. (i,j)\in\mathcal M\times\mathcal M$

Definícia2 (Klasická priraďovacia úloha KPU)

Medzi najznámejšie inštancie rozvrhovacích úloh patrí klasická priraďovacia úloha. Nech $M,|M|=m$ je konečná množina, $\mathbb C$ typu $m\times m$ je daná matica reálnych čísel a $\mathbb X$ typu $m\times m$ je hľadaná matica priradení. Potom priraďovaciu úlohu možno formulovať ako nasledujúcu úlohu bivalentného lineárneho programovania.

$\begin{array}{c} \min Z = \sum_{i\in M} \sum_{j\in M}{c_{ij}x_{ij}} \\ s.t. \\ \sum_{i\in M}x_{ij} = 1, \quad pre \quad \forall j\in M, \\ \sum_{j\in M}x_{ij} = 1, \quad pre \quad \forall i\in M, \\ x_{ij}\in\{0,1\}, \quad pre \quad \forall (i,j)\in M^2 \end{array}$

Aby sme vyriešili ${\mathcal MPP2c}$ pomocou ${\mathcal KPU}$ , potrebujeme správne navrhnúť účelovú funkciu, t.j. prvky matice $\mathbb C$ . Pre štandardný postup [2] nám poslúži miera nerovnomernosti (2). Po jednoduchej úprave získavame nasledujúci tvar

$f_{ssqr}(s_1,s_2,\dots,s_m) = \frac{1}{m}\sum_{i=1}^{m}s_i^2 - \bar{s}^2$

(4)

Za predpokladu že permutácia prvého stĺpca je identická, je $s_i = a_{i1} + a_{\psi_{i2} 2}$ . Hodnoty $\frac{1}{m}$ a $\bar{s}^2$ sú konštantné a neovplyvňujú výsledok optimalizácie, preto ich z účelovej funkcie môžeme vypustiť. Za predpokladu $\psi_{i2} = j$ , môžeme písať prvok matice $\mathbb C$ ako $c_{ij} = (a_{i1} + a_{j2})^2$ pre všetky $(i,j)\in\mathcal M\times\mathcal M$

Exaktné výsledky dvojstĺpcovej varianty ${\mathcal MPP2c}$ používajú na výpočet všeobecnejšieho ${\mathcal MPP}$ problému heuristické metódy riešenia (viď. stochastická dekompozičná metóda).

Čo ale ak potrebujeme nahradiť niektoré alebo všetky prvky matice $\mathbb A$ neistými hodnotami (fuzzy číslami, fuzzy intervalmi)? V takomto prípade potrebujeme definovať novú mieru nerovnomernosti, ktorá vie pracovať s neistými číslami. S touto problematikou sa zaoberá nasledujúca sekcia.

3. Inferenčná miera nerovnomenosti

Navrhnime teraz nerovnomernosti, ktorej vstupným argumentom môže byť ako vektor reálnych čísel, tak aj vektor fuzzy čísel a intervalov. Na návrh takejto miery nerovnomernosti požijeme fuzzy inferenčný systém.

Aby sme mohli vyriešiť ${\mathcal MPP2c}$ problém pomocou ${\mathcal KPU}$ , potrebujeme správne navrhnúť účelovú funkciu, t.j. prvky matice $\mathbb C$ . Postup návrhu inferenčnej miery nerovnomernosti uvedieme v nasledovnom príklade na problematike $\mathcal{MPP}2c$ .

Príklad 1 (Ilustračný príklad riešenia ${\mathcal MPP2c}$ pomocou ${\mathcal FIS}$ )

Majme už existujúci s-dňový rozvrh pre piatich vodičov $(m = 5)$ a pre $(s+1)$ -vý deň chceme nájsť také priradenie i-teho vodiča k j-temu turnusu, aby index preferencie $c_{ij}$ spojený s týmto priradením bol maximálny, pričom musíme každému vodičovi priradiť práve jeden turnus (h1) a každému turnusu priradiť práve jedného vodiča (h2). Nech prvý stĺpec dvojstĺpcovej matice $\mathbb A$ odpovedá kumulovaným výkonom [min] piatich vodičov po s-tý deň a druhý stĺpec matice odpovedá pracovným časom [min] piatich turnusov, o ktorých ešte len máme rozhodnúť, ktorému vodičovi budú priradené.

Zadanie chceme riešiť pomocou priraďovacej úlohy (3), pre ktorú sú obe podmienky (h1,h2) splnené. Ostáva nám iba správne navrhnúť účelovú funkciu, t.j. prvky matice $\mathbb C = (c_{ij})$ , ktoré spočítame pomocou fuzzy inferenčného systému, pre každé $i\in\mathcal M=\{1,2,3,4,5\}$ a pre každé $j\in\mathcal M$ samostatne, tzn., že vykonáme 25 fuzzy inferencií.

Výhodou použitia fuzzy inferenčného systému je, že vyjadrí hodnoty matice $\mathbb C$ aj pre fuzzy vstupy, tzv. pre fuzzy maticu $\mathbb A$ . Teda nemusíme navrhovať žiadnu novú mieru nerovnomernosti pracujúcu s fuzzy číslami. Pre jednoduchosť riešme túto úlohu pre reálnu maticu, ktorej prvky sú fuzzy singletony

$\mathbb A=\left( \begin{array}{cc} 7200 & 420 \\ 7680 & 660 \\ 7080 & 480 \\ 7320 & 540 \\ 7500 & 360 \end{array} \right)$

Nami navrhovaný fuzzy inferenčný systém má dve reálne vstupné hodnoty $x_1$ a $x_2$ , ktoré sa zobrazujú do príslušných fuzzy množín (hodnôt fuzzy lingvistických premenných) a jednu reálnu výstupnú hodnotu y.

Báza dát pozostáva z dvoch fuzzy lingvistických premenných $A, B$ , ktoré sú potrebné pri fuzzyfikácií, t.j. pri určovaní stupňa, ktorým jednotlivé vstupy prislúchajú fuzzy lingvistickým hodnotám, ktoré definujeme pomocou funkcií príslušnosti. Nech $A$ je fuzzy lingvistická premenná vyjadrujúca denný kumulovaný pracovný čas vodiča nadobúdajúca nasledujúce hodnoty (obr. 1(a)):

VS – Very short working cumulated time
S – Short working cumulated time
A – Average working cumulated time
L – Long working cumulated time
VL – Very long working cumulated time

(a) Fuzzy lingvistická premenná $A$ vyjadrujúca kumulovaný denný pracovný čas vodiča s danými funkciami členstva fuzzy množín VS, S, A, L, VL

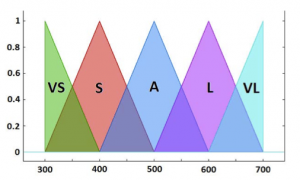
(b) Fuzzy lingvistická premenná $B$ vyjadrujúca denný pracovný čas turnusu a jej funkcie členstva fuzzy množín VS, S, A, L, VL
Fig.1 Vstupné fuzzy lingvistické premenné

Nech $B$ je fuzzy lingvistická premenná vyjadrujúca denný pracovný čas turnusu, ktorá nadobúda nasledujúce hodnoty (obr. 1(b)):

VS – Very short working time
S – Short working time
A – Average working time
L – Long working time
VL – Very long working time

Ďalej báza dát pozostáva z fuzzy lingvistickej premennej $C$ , ktorá je potrebná v procese inferencie na získanie výslednej hodnoty (plochy) uvažovaného lingvistického pravidla (AK – POTOM). Nech $C$ je fuzzy lingvistická premenná vyjadrujúca index preferencie a nadobúda nasledujúce hodnoty (obr. 2).

VLP – Very low preference
LP – Low preference
MP – Medium preference
HP – High preference
VHP – Very high preference

Fig. 2. Fuzzy lingvistická premenná C vyjadrujúca index preferencie a jej funkcie členstva fuzzy množín VLP, LP, MP, HP, VHP

Báza lingvistických pravidiel pozostáva z nasledujúcich piatich pravidiel:

$R_1: \text{ AK } (x_1 \text{ je VS } \wedge x_2 \text{ je VL }) \vee (x_1 \text{ je VL } \wedge x_2 \text{ je VS }),$

$\text{POTOM } y \text{ je VHP}$

$R_2: \text{ AK } ((x_1 \text{ je VS } \wedge x_2 \text{ je L }) \vee (x_1 \text{ je S } \wedge x_2 \text{ je VL })) \vee$

$\vee ((x_1 \text{ je L } \wedge x_2 \text{ je VS }) \vee (x_1 \text{ je VL } \wedge x_2 \text{ je VS } )), \text{ POTOM } y \text{ je HP }$

$R_3: \text{ AK } ((x_1 \text{ je VS } \wedge x_2 \text{ je A } ) \vee (x_1 \text{ je S } \wedge x_2 \text{ je L } ) \vee$

$\vee (x_1 \text{ je A } \wedge x_2 \text{ je VL } )) \vee ((x_1 \text{ je A } \wedge x_2 \text{ je VS } ) \vee$

$\vee (x_1 \text{ je L } \wedge x_2 \text{ je S } ) \vee (x_1 \text{ je VL } \wedge x_2 \text{ je A } )), \text{ POTOM } y \text{ je MP }$

$R_4: \text{ AK } ((x_1 \text{ je VS } \wedge x_2 \text{ je S } ) \vee (x_1 \text{ je S } \wedge x_2 \text { je A } ) \vee$

$\vee (x_1 \text{ je A } \wedge x_2 \text{ je L } ) \vee (x_1 \text { je L } \wedge x_2 \text { je VL } )) \vee$

$\vee ((x_1 \text { je S } \wedge x_2 \text{ je VS } ) \vee (x_1 \text { je A } \wedge x_2 \text{ je S } ) \vee$

$\vee (x_1 \text{ je L } \wedge x_2 \text{ je A } ) \vee (x_1 \text{ je VL } \wedge x_2 \text{ je L } )), \text{ POTOM } y \text{ je LP}$

$R_5: \text { AK } (x_1 \text{ je VS } \wedge x_2 \text{ je VS } ) \vee (x_1 \text{ je S } \wedge x_2 \text{ je S } ) \vee$

$\vee (x_1 \text{ je A } \wedge x_2 \text{ je A } ) \vee (x_1 \text{ je L } \wedge x_2 \text{ je L } ) \vee$

$\vee (x_1 \text{ je VL } \wedge x_2 \text{ je VL } ), \text { POTOM } y \text { je VLP }$

Vidíme, že takto zapísaná báza lingvistických pravidiel je dosť nečitateľná a preto ju zjednodušíme a zapíšeme pomocou nasledujúcej tabuľky:

Báza pravidiel

y		x₂
		VS	S	A	L	VL
x₁	VS	VLP	LP	MP	HP	VHP
	S	LP	VLP	LP	MP	HP
	A	MP	LP	VLP	LP	MP
	L	HP	MP	LP	VLP	LP
	VL	VHP	HP	MP	LP	VLP

Zadefinujme si teraz dve vstupné a jednu výstupnú hodnotu fuzzy inferenčného systému:

Prvou vstupnou hodnotou je $x_1 = a_{i1}$ ,
druhou vstupnou hodnotou je $x_2 = a_{j2}$ a
výstupnou hodnotou je $c_{ij} = y$ .

Tieto vstupy a výstupy definujeme pre každé $(i,j)\in\mathcal M\times\mathcal M$ . Teraz môžeme použiť nástroj [7] (aplikáciu), ktorým vyriešime takto navrhnutý fuzzy inferenčný systém aplikovaním Mamdamiho inferenčnej metódy. Postup inferencie pre dané vstupy $x_1 = 7200$ a $x_2 = 420$ s výslednou hodnotou $y = 22.5$ môžeme vidieť na obrázku 3. Výsledok inferencie y patriaci do intervalu [0,100] pre všetky vstupné hodnoty $x_1\in [7000, 8000]$ a $x_2\in [300, 700]$ sme spočítali pomocou balíčka pyFuzzy [6] v programovacom prostredí Python [5] a môžeme ho vidieť na obrázku 4. A matica $\mathbb C = (c_{ij})$ je rovná hodnotám

$\mathbb C=\left( \begin{array}{cccccc} 22.90 & 64.47 & 32.13 & 43.89 & 20.73 \\ 40.25 & 30.88 & 31.07 & 24.30 & 51.83 \\ 30.52 & 71.25 & 39.65 & 51.17 & 24.30 \\ 18.25 & 54.46 & 26.17 & 34.36 & 28.03 \\ 27.34 & 41.61 & 16.40 & 20.73 & 38.39 \end{array} \right)$

Po vyriešení priraďovacej úlohy získame maticu priradení $\mathbb X = (x_{ij})_{m\times m}$

$\mathbb X=\left( \begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{array} \right)$

pre ktorú podľa predpisu

$x_{ij} = \left\{ \begin{array}{ccc} 1 & \text{potom} & \psi_{i1} = i, \psi_{i2} = j \\ 0 & \text{nic nerob} & \end{array} \right. (i,j)\in\mathcal M\times\mathcal M$

spočítame usporiadanú dvojicu (maticu permutácií (1)) $\Psi = (\psi_1, \psi_2)$ optimálnych permutácií

$\Psi=\left( \begin{array}{cc} 1 & 2 \\ 2 & 5 \\ 3 & 4 \\ 4 & 3 \\ 5 & 1 \end{array} \right)$

pre ktoré obdržíme nasledujúci rozvrh

$\mathbb A^{\Psi}=\left( \begin{array}{cc} 7200 & 660 \\ 7680 & 360 \\ 7080 & 540 \\ 7320 & 480 \\ 7500 & 420 \end{array} \right)$

s kumulovanými pracovnými časmi vodičov $s^{\Psi} = (7860, 8040, 7620, 7800, 7920)$ .

Fig.3 Inferenčný proces Mamdamiho metódy pre dané vstupné hodnoty $x_1 = 7200$ a $x_2 = 420$ s výslednou hodnotou $y = 22.5$

Fig.4 Výsledný graf fuzzy inferencie pre všetky vstupy.

4 Záver

Článok sa venoval problematike návrhu miery nerovnomernosti v problematike rovnomerných rozvrhoch pri neistote a to za pomoci fuzzy inferenčného systému. Výhoda tohoto prístupu spočíva v tom, že vstupný argument môže obsahovať reálne hodnoty a aj fuzzy čísla. Použitie inferenčnej miery nerovnomernosti sme demonštrovali na ilustračnom príklade riešenia $\mathcal{MPP}2c$ problematiky, kvôli jednoduchosti, s reálnou maticou a za pomoci Mamdamiho inferenčnej metódy.

Poďakovanie

Táto práca vznikla s podporou grantovej agentúry VEGA vrámci riešenia projektu 1/0374/11 Modelovanie a optimalizácia mobility a infraštruktúry v logistických sieťach.

References

Graham, R.L., Lawler, E.L., Lenstra, J.K., Rinnooy Kan, A.H.G., Optimization and Approximation in Deterministic Sequencing and Scheduling: A Survey, 1979
Peško, Š., Optimalizácia NP-ťažkých dopravných rozvrhov, ŽU Žilina, Habilitačná práca, 2002
Peško, Š., The Matrix Permutation Problem in Interval Arithmetic, Journal of Information, Control and Management Systems, vol. 1, num. 1, 2006
Teodorovič, D., Lučić, P., A fuzzy set theory approach to the aircrew rostering problem, Fuzzy Sets and Systems, vol. 95, num. 3, pp. 261-277, 1998
Python, Python Programming Language, Programming Language,
www.python.org
pyFuzzy, Python fuzzy package,
pyfuzzy.sourceforge.net
MATLAB, numerical computing environment, the matlab fuzzy toolbox

O časopise

Meta

RSS

Inferenčná miera nerovnomernosti

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív