Edge detection improves image readability and it is an important part of images preprocessing aimed to their segmentation and automatic recognition of their contents. This paper describes selected methods of edge detection in magnetic resonance images, with the emphasis on the wavelet transform use.

The first part briefly describes the mathematical background of the wavelet transform, including its properties and application in image processing. Modulus Maxima Method by Stephane Mallat provides the method for edge detection using wavelet transform. This method is based on finding local maxima of horizontal and vertical wavelet coefficients in the first level of wavelet decomposition. It is supposed that this level represents edges. This method was tested with various wavelet functions both on simulated and real medical images.

A complex wavelet function use could help to improve results of edge detection in real images. Presented paper contains a comparison of basic edge detection methods including simple gradient operators and Canny edge detector, and their combination with wavelet transform use. Mathematical principals were studied, as well as application of these methods. All algorithms were developed in the MATLAB environment using Wavelet and Image Processing Toolboxes.

1. 2D Discrete Wavelet Transform

2D Discrete Wavelet Transform (2D DWT) [1, 6] is used in image processing as a powerful tool solving to image analysis, denoising, image segmentation and other. 2D DWT can be applied as a convolution of a selected wavelet function with an original image or it can be seen as a set of two matrices of filters, row and column one. Using a separability property of DWT, the first part of decomposition consists of an application of row filters to the original image. The column filter are used for further processing of image resulting from the first step. This image decomposition [1] can by mathematically described by Eq. (1)

(1)

where is the final matrix of wavelet coefficients, represents an original image, is a matrix of row filters and \textbf{Y} is a matrix of column filters.

In the first level of decomposition of 2D DWT, the image is separated into four parts. Each of them has a quarter size of the original image [6]. They are called approximation coefficients (LowLow or LL), horizontal (LowHigh or LH), vertical (HighLow or HL) and detail coefficients (HighHigh or HH) [2, 6], see Fig.1. Approximation coefficients obtained in the first level can be used for the next decomposition level. Inverse 2D Discrete Wavelet Transform used in image reconstruction is defined by Eq. (2)

(2)

For the orthogonal matrices this formula can be simplified into Eq. (3)

(3)

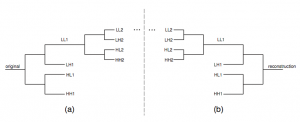
Figure 1: 2D DWT decomposition into two levels: (a) Image decomposition, (b) Image recon- struction, (c) Scheme of decomposition up to the second level

2. Edge Detection Methods Using Wavelet Transform

This paper deals with several methods of edge detection using wavelet transform. MRI images were processed by mentioned methods. Image thresholding and median filtering were used for images preprocessing. Daubechies, Symlet and Coiflet function families were studied in the treatment of real images.

2.1 Simple Method Using Modification of Approximation Coefficients

2D DWT decomposition separates an image into the four parts, each of them contains different information of the original image. Detail coefficients represent edges in the image, approximation coefficients are supposed to be a noise. A proper modification of approximation coefficients is the easiest way for edge detection.

2.1.1 Approximation coefficients replaced by zeros

The principle of the simplest method of edge detection is based on replacing of all approximation coefficients by zeros. This modification removes low frequencies from the image. The image is reconstructed using only the remaining wavelet coefficients. By means of this method the most expressive edges are found.

Figure 2: MR image – an area with a brain tumor: (a) Original image, (b) Edges found by replacing approximation coefficients by zeros (using Haar wavelet function), (c) Edges projection into the original image

2.1.2 Modification of approximation coefficients by simple edge detectors

Another method of edge detection is a modification of approximation coefficients by other simple edge detector such as Canny, Sobel, Prewitt, etc. [3]. The simple detector is applied to the approximation coefficients obtained in the first level of decomposition. The image is reconstructed from remaining coefficients and from modified approximation coefficients. This method provides sufficient results, especially with Canny detector use.

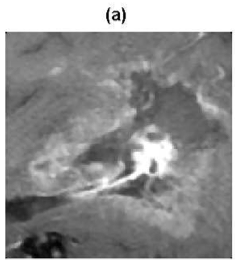
Figure 3: MR image – an area with a tumor: (a) Original image, (b) Edges found by Canny detector applied to the approximation coefficients, (c) Edges projection into the original image

2.2 Wavelet Transform Modulus Maxima Method

This method was developed by Stephane Mallat [4, 5]. Its principle is based on finding local maxima of wavelet coefficients (Wavelet Transform Modulus Maxima Method), which repre- sent the edges in the image. The method uses only horizontal and vertical coefficients values (LowHigh and HighLow coefficients 1) from each level of wavelet decomposition. Wavelet transform modulus is defined by Eq. (4)

(4)

for each pair of horizontal and vertical coefficients
a at the same position in matrices. A matrix of the gradient angles for the same pairs of coefficients is evaluated according to Eq. (5)

(5)

Points in the original image for which values of are local maxima in one-dimensional neighborhood in the direction of gradient are supposed to be edge pixels. These points are distributed according the boundary of important structures in the image. To recover edges, found individual maxima are chained.

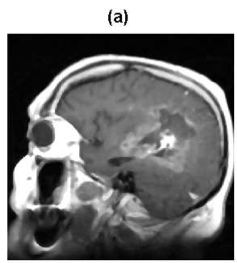
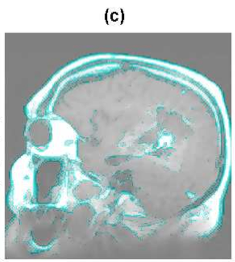
Figure 4: MR image: (a) Original image, (b) Edges found by wavelet maxima using Haar wavelet function, (c) Edges projection into the original image

3. Results

A comparison of edge detection methods is not easy because of difficult edge determination in the image. Especially in the medical images there is a lot of textures in the image background that makes this task ambiguous. Rating of each method is attitudinal. Methods mentioned in part 2 were tested in the set of the MR images using different wavelet functions.

Methods which use a modification of approximation coefficients, provide the simplest way to edge detection using wavelet transform. A method using approximation coefficients replacing by zeros finds edges well but edges are bad located, see Fig. 2. This method also locates a lot of false edges coming from textures in the image background.

The method that applies simple detector to approximation coefficients provides better results; a dependency upon a detector used must be mentioned, as well. Gradient detectors, such as Sobel or Prewitt, return acceptable edges but these edges are bad located, again the best results are provided by Canny detector, see Fig. 3.

The Wavelet Transform Modulus Maxima Method finds edges in all directions in image. Its results seems to be not sufficient for edge detection. Although the comparison between directions of gradient has been set up very leniently, edges found are not connected, see Fig. 4, 5. A complex wavelet function use could help to improve results of edge detection in real images.

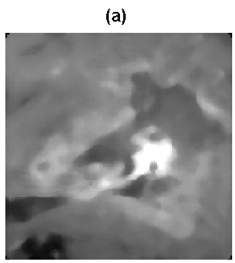
Figure 5: MR image – an area with the tumor: (a) Original image, (b) Edges found by wavelet maxima using Haar wavelet function, (c) Edges projection into the original image

4. Acknowledgement

This work has been supported by the Ministry of Education of the Czech Republic (program No. MSM 6046137306).

References

1. Mauro Barni. Document and Image Compression. CRS Press, Taylor and Francis Group, 2006.
2. Al Bovik. The Essentuial Guide to Image Processing. Elsevier, Inc., second edition, 2009.
3. Rafael C. Gonzalez and Richard E. Woods. Digital Image Processing. Pearson Education, Inc., Upper Saddle River, New Jersey, third edition, 2008.
4. Stephane Mallat. A Wavelet Tour Of Signal Processing. Academic Press, 1998.
5. Stephane Mallat and Sifen Zhong. Characterization of signals from multiscale edges. IEEE TRANSACTION ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, 14(7):23, July 1992.
6. Truong Q.Nguyen. A tutorial on filter banks and wavelets. University of Wisconsin, ECE Department, June 1995.

---

Coauthor of this paper is E. Hošťálková Department of Computing and Control Engineering Institute of Chemical Technology, Prague