Aplikace simulačních metod pro zjištění tepelného chování systémů v budovách – 2. část
18. Júl, 2011, Autor článku: Gerlich Vladimír, Elektrotechnika, MATLAB/Comsol
Ročník 4, číslo 7  Pridať príspevok
Pridať príspevok
![]() Přenos tepla v budovách, resp. mezi budovou a jejím okolím, se stal během uplynulých dvou desetiletí často řešenou problematikou. Vnitřní teplota budovy totiž ovlivňuje nejen spokojenost uživatelů obytných budov, ale také pracovní výkonnost ať pracovníků (nejen) v administrativních budovách. Z tohoto důvodu je vhodné, aby obyvatelé budov byli spokojeni s kvalitou vnitřního prostředí. Přenos tepla mezi budovou a jejím okolím výrazně ovlivňuje náklady na vytápění/chlazení, což zejména v posledních letech, kdy se zdražuje cena energií, začínají chápat i koncoví uživatelé jako důležitý faktor při nákupy domu nebo bytu.
Přenos tepla v budovách, resp. mezi budovou a jejím okolím, se stal během uplynulých dvou desetiletí často řešenou problematikou. Vnitřní teplota budovy totiž ovlivňuje nejen spokojenost uživatelů obytných budov, ale také pracovní výkonnost ať pracovníků (nejen) v administrativních budovách. Z tohoto důvodu je vhodné, aby obyvatelé budov byli spokojeni s kvalitou vnitřního prostředí. Přenos tepla mezi budovou a jejím okolím výrazně ovlivňuje náklady na vytápění/chlazení, což zejména v posledních letech, kdy se zdražuje cena energií, začínají chápat i koncoví uživatelé jako důležitý faktor při nákupy domu nebo bytu.
2. Problematika přenosu tepla v budovách
Problematika sdílení tepla mezi budovou a jejím okolím jako i mezi vnitřními částmi budovy je založena na přenosu tepla popsaném v předchozích kapitolách. Z důvodu značné náročnosti dynamického popisu sdílení tepla a také značnou komplexností vztahů v prostředí budov je tento proces nejčastěji řešen pomocí zjednodušených metod anebo numericky.
Následující kapitoly představují teoretické poznatky důležité při modelování přenosu tepla, stručný popis tvorby numerického modelu místnosti a upozorňují na nejistoty těchto simulačních metod.
2.1 Stacionární vedení tepla pro modelování teplotní odezvy budovy
Rozdíl mezi náročností popisu stacionárního a nestacionárního děje lze odvodit už jen dle délky této a následující kapitoly. Zatímco u stacionárního vedení tepla se pro 1-rozměrný problém jedná o vyřešení Obyčejné Diferenciální Rovnice (ODR) 2. řádu, tak u nestacionárního popisu je třeba navíc řešit i časovou derivaci a výsledná rovnice je také závislá na typu okrajové podmínky. Průběh teploty v desce (ve stěně) bez vnitřních zdrojů tepla tak lze popsat rovnicí:
| (8) |
Řešením rovnice (8) pro 1-dimensionální přestup tepla mezi body T1, T2 je lineární rovnice
| (9) |
2.2 Nestacionární vedení tepla pro modelování teplotní odezvy budovy
Modely komplexních struktur jakými jsou budovy a jejich části, jsou díky velkému množství vazeb komplikované, a nelze je proto řešit analytickými metodami. Přistupuje se tak na jedné straně k řešení přenosu tepla pomocí zjednodušených postupů nebo k jeho matematickému modelování a řešení pomocí numerických metod. Zde je třeba připomenout, že ani numerická řešení nejsou použitelná pro všechny případy geometrií staveb a i u nich je třeba zavádět jistá zjednodušení.
Okrajové podmínky jsou v prostředí budov často časově proměnné (změna okolní teploty), přestože se obecně ve výpočtech dle norem uvažují jejich konstantní hodnoty. Z tohoto důvodu bude v této práci uvažováno s jejich konstantní hodnotou, přestože pro numerické řešení nestacionárního vedení tepla není tento předpoklad potřeba dodržet. Protože se v prostředí budov počítá s teplotou ve °C namísto K, tak budou v následujících vztazích tyto hodnoty teploty popisovány znakem . Nestacionární teplotní pole v rovinné desce je dáno řešením rovnice:
| (10) |
Tuto rovnici lze řešit analyticky pomocí separace proměnných při zadaných okrajových a počátečních podmínkách. Pro zjednodušení je tato rovnice obvykle řešena při výpočtech v prostředí budov v jednorozměrném tvaru.
Pro počáteční teplotu stěny a okrajovou podmínku 1. druhu je průběh teploty v desce popsán rovnicí:
| (11) |
kde člen je roven lichým násobkům
| (12) |
Pro počáteční teplotu stěny a okrajovou podmínku 3. druhu lze analogicky odvodit vztah
| (13) |
kde člen je tentokrát dán kořeny transcendentní rovnice:
| (14) |
Díky následné nutnosti výpočtu periodické okrajové podmínky (14) se řešení rovnice (13) stává ještě více komplikovaným. Z uvedených informací o řešení nestacionární rovnice vedení tepla je patrné, že čím více je komplikovaný popis okrajové podmínky, tím komplikovanější je i vlastní rovnice popisující teplotní pole.
2.3 Zjednodušené metody
Jedná se zejména o zjednodušení výpočtu akumulační schopnosti budov nebo výpočtu výkonu otopného tělesa v době zátopu [9]. Zjednodušené výpočty průběhu teplot místnosti jsou představeny v [7] nebo [8]. Zjednodušení se často projevuje popisem problému přenosu tepla pomocí ODR 1. řádu nebo snížením počtu prostorových souřadnic (nejčastěji se řeší 1-dimensionální problém přenosu tepla).
Tento postup umožňuje relativně snadné a rychlé vypočtení potřebných hodnot, ale zároveň vnáší do výsledku chybu danou zjednodušeným řešením PDR 2. řádu. Alternativním postupem je řešení uvedeného problému pomocí numerických metod, pomocí nichž lze následně zhodnotit vhodnost použití jednotlivých zjednodušených výpočetních postupů. Na druhou stranu je při numerickém modelování brát ohled na možné potíže s tvorbou sítě a numerickou nestabilitou řešení.
2.4 Numerické modelování
Nejen výpočty přenosu tepla se čím dál obvykleji řeší numericky pomocí metod konečných prvků, objemů nebo diferencí, který využívají rozdělení řešeného prostoru do sítě a výpočtu hodnot závislých fyzikálních veličin v jejích bodech. Mezi nejznámější metody pro numerické řešení ODR patří [18]:
- Jednokrokové metody (Eulerova metoda, Metoda Runge-Kutta).
- Vícekrokové metody (Adamsovy metody).
- Extrapolační metody.
Mezi nejznámější metody pro numerické řešení PDR patří [18]:
- Metoda sítí.
- Variační metody.
- Metoda konečných prvků (MKP).
Jednou z nejpoužívanějších metod v moderní výpočetní technice je MKP. Tato metoda je vhodná pro simulaci průběhů napětí, deformací, proudění tepla nebo proudění tekutin na vytvořeném fyzikálním modelu. Přestože je její princip znám již delší dobu (počátky vývoje sahají do 40. let 20. století), tak k jejímu širšímu využití došlo teprve s nástupem počítačů s dostatečným výkonem pro její výpočet (zejména paměti – RAM).
MKP využívá rozklad oblasti na trojúhelníky nebo čtyřúhelníky, jedná-li se o řešení ve 2D, resp. na čtyřstěny nebo šestistěny ve 3D. Příklad 3D sítě na tvořeném modelu místnosti je zobrazen na obrázku 1. Rozkladem oblasti s nepravidelným tvarem na tyto útvary se dopouštíme na okraji řešeného objektu chyby, kterou lze zmenšit zjemněním rozkladu.
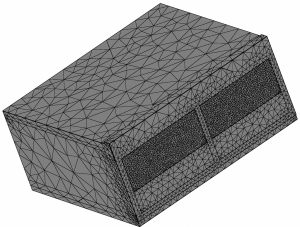
Obr. 1 – Vytvořená síť MKP na modelu laboratoře
Po provedení diskretizace modelu dochází k výpočtu soustavy algebraických rovnic pomocí zadaných okrajových podmínek s následným výpočtem jednotlivých veličin. Z naznačeného postupu je patrné, že pro obdržení dostatečně kvalitního řešení je třeba vytvořit síť s vhodnou hustotou a rozložením jejich prvků. Dalším parametrem, který ovlivňuje přesnost řešení je nastavení akceptovatelné chyby numerického postupu (MKP patří k numerickým metodám, které nedávají přesný, ale pouze přibližný výsledek).
2.4.1 Nepřesnosti numerického modelování
Mezi parametry ovlivňující přesnost numerických simulací patří zejména vhodně zvolená hustota a rozložení jednotlivých prvků sítě a nastavená přesnost numerického řešení. Vybraný nástroj pro numerické modelování umožňuje ve své aktuální verzi automatickou tvorbu sítě s ohledem na řešený fyzikální proces, a tak např. při pohybu tekutiny v potrubí dojde k vytvoření hustší sítě na rozhraní mezi kapalinou a stěnou.
2.4.2 Výběr programu pro tvorbu numerického modelu
Pro řešení nestacionárního přenosu tepla v budovách bylo nejprve třeba vybrat software pro tvorbu modelu. Hlavní kritéria, které musel program pro výpočet přenosu tepla splnit jsou:
- Schopnost programu řešit PDR.
- Tvorba geometrie modelu přímo v daném prostředí (bez značného zjednodušení) nebo možnost jejího importu z CAD programů.
- Umožnění exportu výsledků simulace pro následné zpracování v jiných programech.
- Názorná interpretace simulačních výsledků.
Po zkušenostech s předchozím použitím nástroje COMSOL Multiphysics [19] na řešitelově pracovišti [20], [21], ale i díky jeho přednostem představeným v [12] bylo vybráno pro tvorbu numerického modelu místnosti právě toto prostředí. Kromě tohoto softwaru bylo zvažováno i použití nástrojů ESP-r [22]. Přes značné využívání tohoto nástroje pro obdobné problémy na vysokých školách po celém světě, program nesplnil požadavky kladené na použitelnost nástroje a i díky problémům představených v [23] bylo od použití tohoto programu upuštěno.
Na rozdíl od specializovaných nástrojů pro modelování vnitřního prostředí v budovách jakými jsou ESP-r nebo TRNSYS [24] neslouží vybraný program pouze k simulaci jednoho fyzikálního děje, ale jedná se o program pro obecné řešení PDR pomocí MKP. Samotný název programu odkazuje na schopnost prostředí simulace několika fyzikálních dějů, které se vzájemně ovlivňují.
2.4.3 Realizace numerického modelu místnosti
Nejprve byla ověřena základní funkčnost simulačního prostředí s využitím knihovny příkladů a modelováním typů úloh, které lze vyřešit analyticky. Při těchto srovnáních byla ověřena důležitost tvorby sítě a nastavení maximální chyby numerického řešení, při jejichž nevhodném nastavení docházelo k systematické chybě mezi teplotou získanou numericky a analyticky. Po tomto kroku bylo následně přistoupeno k vytvoření modelu místnosti.
Byl vytvořen model laboratoře umístěné v nejvyšším patře křídla budovy Fakulty Aplikované Informatiky (FAI). Půdorys laboratoře a jejího okolí jsou zobrazeny na obrázku 2. Tři stěny modelované místnosti sousedí s okolními učebnami nebo chodbou. Pod laboratoří se nachází učebna a teplota v laboratoři je tak ovlivňována venkovním prostředím vnější stěnou s okny a stropem. Tyto povrchy tak mají zásadní vliv na ztrátový prostup tepla z místnosti.

Obr. 2 – Okolí modelované místnosti
2.4.4 Tvorba geometrie objektu
Geometrie modelu, při jejímž kreslení byly použity stavební výkresy budovy FAI, je zobrazena na obrázku 3. Přestože lze v programovém prostředí COMSOL Multiphysics nakreslit základní geometrické tvary, tak tvorba natolik komplikovanému objektu nebyla v programu možná, a tak musela být do programu importována pomocí .stp souboru z programu pro 3-dimensionální konstruování. Pro její nakreslení lze využít široké spektrum CAD programů z důvodu značného rozšíření možnosti exportu do tohoto typu souboru.
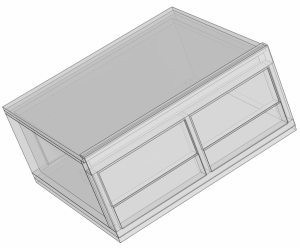
Obr. 3 – Geometrie modelu místnosti
2.4.5 Tvorba numerického modelu
Takto vytvořený model byl následně v programu COMSOL Multiphysics doplněn o fyzikální rovnice popisující přenos tepla s příslušnými okrajovými podmínkami. Okrajové podmínky jsou zadány pomocí funkcí, a umožňují tak variabilitu těchto podmínek v čase (vhodné zejména pro import hodnot proměnné venkovní teploty). Základní bilanční rovnice, kterou numerický model počítá pro jednotlivé domény je ve tvaru:
| (15) |
První část rovnice popisuje přenos tepla vedením, druhá část přenos tepla zapříčiněný pohybem částic (s tímto členem bylo uvažováno pouze ve vnitřním vzduchu) a třetí člen rovnice popisuje tepelnou akumulaci daného elementu. Další důležité rovnice pro přenos tepla popisují okrajové podmínky. Na vnějších površích bylo počítáno s okrajovou podmínkou 3. druhu a na vnitřních površích je počítáno s paralelní kombinací přestupu tepla pomocí okrajové podmínky 3. druhu a sálání. Tvořený model tak využívá paralelní kombinace vedení, proudění a sálání.
Poděkování
Práce na této publikaci byla podpořena Evropským Fondem pro Regionální Rozvoj při projektu CEBIA-Tech No. CZ.1.05/2.1.00/03.0089 a dále interní grantovou agenturou Univerzity Tomáši Bati ve Zlíně s číslem IGA/44/FAI/10/D.
Použitá literatura a zdroje
- ČSN EN ISO 13792. Tepelné chování budov : Výpočet vnitřních teplot v místnosti v letním období bez strojního chlazení – Zjednodušené metody. [s.l.] : Český normalizační institut, 2005. 49 s.
- ČSN 73 0540-1. Tepelná ochrana budov – Část 1: Terminologie. Praha : [s.n.], 2005. 68 s.
- ČSN 73 0540-2. Tepelná ochrana budov – Část 2: Požadavky. Praha : [s.n.], 2007. 44 s.
- ČSN 73 0540-3. Tepelná ochrana budov – Část 3: Návrhové hodnoty veličin. Praha : [s.n.], 2005. 96 s.
- ČSN 73 0540-4. Tepelná ochrana budov – Část 4: Výpočtové metody. Praha : [s.n.], 2005. 60 s.
- ČSN EN 12831. Tepelné soustavy v budovách : Výpočet tepelného výkonu. [s.l.] : Český normalizační institut, 2005. 73 s.
- ČSN 06 0220. Tepelné soustavy v budovách – Dynamické stavy. Praha : [s.n.], 2006. 20 s.
- ČSN EN ISO 13790. Energetická náročnost budov – Výpočet spotřeby energie na vytápění a chlazení. Praha : [s.n.], 2006. 140 s.
- ŘEHÁNEK, Jaroslav. Tepelná akumulace budov. 1. vydání. Praha : Informační centrum České komory autorizovaných inženýrů a techniků činných ve výstavbě, 2002. 280 s. ISBN 80-86364-59-3.
- SCHELLEN, H.L.; SCHIJNDEL, A. W. M. van; BRIGGEN, P. M. The use of COMSOL for Building Constructions Engineering regarding Heat and Moisture Transport. In Proceedings of the COMSOL Conference 2008 Hannover. [s.l.] : [s.n.], 2008. s.
- VOGEL, Petr, et al. Rozdělení spotřeby tepla na vytápění na příkladu panelového domu. TZB-info – stavebnictví, úspory energií, technická zařízení budov [online]. 22.11.2010, [cit. 2011-02-15]. Dostupný z WWW: <http://stavba.tzb-info.cz/regenerace-bytovych-domu/6952-rozdeleni-spotreby-tepla-na-vytapeni-na-prikladu-paneloveho-domu#english_synopsis>. ISSN 1801-4399.
- SCHIJNDEL, Jos van. Integrated Modeling using MatLab, Simulink and COMSOL: with heat, air and moisture applications for building physics and systems. 2008. Saarbrucken: VDM Verlag Dr. Muller Aktiengesellschaft & Co. KG,. 197 p. ISBN 978-3-639-10669-5.
- SCHIJNDEL, A.W.M. van, et al. Application of an integrated indoor climate, HVAC and showcase. Energy and Buildings. 2008, 40, s. 647–653. [článek]
- ÇENGEL, Yunus A. Heat and mass transfer : a practical approach. Boston : McGraw-Hill, 2007. 901 s. ISBN 0073129305.
- LIENHARD IV, John H.; LIENHARD V, John H. A heat transfer textbook. 4th edition. Cambridge : Phlogiston Press, 2003. 749 s.
- KOLOMAZNÍK, Karel; SEDLÁŘ, Jaroslav; MACHÁČKOVÁ, Alena. Teorie technologických procesů III. první. Brno : Rektorát Vysokého učení technického v Brně, 1978. 139 s. ISBN 55-588-78.
- HEJZLAR, Radko. Sdílení tepla. 3. Praha : ČVUT, 1999. 186 s. ISBN 80-01-01982-9.
- VITÁSEK, Emil. Numerické metody. Praha : SNTL, 1987. 516 s. ISBN 04-009-87.
- Multiphysics Modeling and Simulation Software – COMSOL [online]. 2011 [cit. 2011-06-14]. Multiphysics Modeling and Simulation Software. Dostupné z WWW: <http://www.comsol.com/>.
- ŠIŠÁK, Jiří. Počítačová simulace a modelování výseku objektu pomocí programu FEMLAB. [s.l.], 2006. 97 s. Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky. Vedoucí diplomové práce Ing. Martin Zálešák, CSc.
- MINISTR, Jakub. Optimalizace elektrického ohřevu výměn. Zlín, 2008. 62 s. Diplomová práce. Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky.
- ESP-r [online]. 2011 [cit. 2011-02-28]. ESP-r. Dostupné z WWW: <http://www.esru.strath.ac.uk/Programs/ESP-r.htm>.
- BABICA, Vladimír. Ověření simulační metody ESP-r v rámci laboratoře Inteligentní budovy [online]. [s.l.], 2007. 109 s. Diplomová práce. Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky. Vedoucí diplomové práce Ing. Martin Zálešák, CSc.
- TRNSYS Information [online]. 2011 [cit. 2011-02-28]. The Transient Energy System Simulation Tool. Dostupné z WWW: <www.trnsys.com>.
- GERLICH, Vladimír. Validation Heat Transfer Model by Experimental Measurement. In Proceedings of 12th International Carpathian Control Conference. [s.l.] : [s.n.], 2011. ISBN 978-1-61284-359-9.
- GERLICH, Vladimír. Modelling of Heat Transfer in Buildings. In Proceedings of 25th European Conference on Modelling and Simulation ECMS 2011. [s.l.] : [s.n.], 2011. s. 244. ISBN 978-0-9564944-2-9.
- BEASOLEIL-MORRISON, Ian. Flow responsive modelling of internal surface convection. In Building Simulation : Seventh International IBPSA Conference. Rio de Janeiro : [s.n.], 2001. s. 923-930.
- BEAUSOLEIL-MORRISON, Ian. The adaptive simulation of convective heat transfer at internal building surfaces. Building and Environment. 2002, 37, s. 791 – 806. ISSN 0360-1323.
- IRVING, S. J. Energy program validation: conclusions of IEA Annex I. Computer-aided design. 1982, 14, s. 33-38.
- WALLENTÉN, P. Convective heat transfer coeffcients in a full-scale room with and without furniture. Building and Environment. 2001, 36, s. 743–751. ISSN 0360-1323.
- KHALIFA, Abdul-Jabbar N. Natural convective heat transfer coefficient – a review I. Isolated vertical and horizontal surfaces. Energy Conversion and Management. 2001, 42, s. 491-504. ISSN 0196-8904.
- KHALIFA, Abdul-Jabbar N. Natural convective heat transfer coefficient – a review II. Surfaces in two- and three-dimensional enclosures. Energy Conversion and Management. 2001, 42, s. 505-517. ISSN 0196-8904.
- J.M. Coulson and J.F. Richardson. Chemical Engineering. vol. 1. 4th edition. Pergamon Press. 1990.
1
2
3
Použité symboly
| Bi | [-] | Biotovo číslo |
Biot number |
| t | [s] | Čas | Time |
| l | [m] | Charakteristický rozměr | Characteristic length |
| Fo | [-] | Fourierovo číslo |
Fourier number |
| Gr | [-] | Grashofovo číslo | Grashof number |
| g | [ms-2] | Gravitační zrychlení | Standard gravity |
| q | [Wm-2] | Hustota tepelného toku | Heat flux |
| Nu | [-] | Nusseltovo číslo | Nusselt number |
| x | [m] | Pozice | Position |
| Pr | [-] | Prandtlovo číslo | Prandtl number |
| Re | [-] | Reynoldsovo číslo | Reynolds number |
| v | [ms-2 | Rychlost | Speed |
| h | [Wm-2K-1] | Součinitel přestupu tepla | Heat transfer coefficient |
| cP | [J.kg-1K-1] | Tepelná kapacita | Heat capacity |
| Q | [W] | Tepelný zdroj | Heat source |
| [Km-1] | Teplotní gradient; rozdíl teplot dvou bodů vydělený jejich vzdáleností | Temperature gradient; temperature difference divided by thickness | |
| a | [m2s] | Teplotní vodivost |
Thermal diffusivity |
| d | [m] | Tloušťka | Thickness |
Řecké symboly
| [-] | Emisivita | Emissivity | |
| [kg.m-3] | Hustota | Density | |
| [m2s-1] | Kinematická viskozita | Kinematic viscosity | |
| [-] | Kořen | Root | |
| [K-1] | Součinitel objemové roztažnosti | Volumetric thermal expansion coefficient | |
| [W.m-1K-1] | Tepelná vodivost | Thermal conductivity | |
| [oC] | Teplota | Temperature |
Indexy
| e | Vnější | External |
| p | Počáteční | Initial |
| S | Povrch | Surface |
| L | Tekutina | Liquid |
| si | Vnitřní povrch | Internal surface |

