Detekcia hrán v obraze

10. August, 2011, Autor článku: Haffner Oto, Elektrotechnika, MATLAB/Comsol, Študentské práce
Ročník 4, číslo 8 This page as PDF Pridať príspevok

Cieľom príspevku je spracovanie prehľadu metód detekcie hrán v obraze a porovnanie vlastností metód detekcie hrán implementované v programovacom prostredí Matlab. Jednotlivé metódy boli overené a porovnané na sade umelých obrazoch, ktoré boli ďalej zašumené a rozmazané, a na reálnych obrazoch. Na porovnanie a vyhodnotenie metód detekcie hrán nie je známe objektívne kritérium. Jednotlivé metódy boli overené a porovnané na sade umelých obrázkov, ktoré boli ďalej zašumené a rozmazané, a na reálnych obrázkoch.

1. Úvod

V rôznych úlohách počítačového videnia (3-D rekonštrukcia z viacerých snímok scény) je dôležité nájsť význačné oblasti v obraze, ktoré sa nazývajú črty. Medzi črty patria rohové body a hrany telies. Výsledky neurofyziologického a psychologického výskumu ukazujú, že pre zrakové vnímanie vyšších organizmov sú dôležité miesta v obraze, kde sa náhle mení hodnota jasu. Tieto miesta nesú viac informácie ako ostatné miesta. Hrana je hranica medzi dvoma oblasťami s relatívne rozdielnymi hodnotami jasu. Základnou myšlienkou detekcie hrán je nájsť miesta v obraze, kde sa jas výrazne mení.

V ideálnom prípade použitie hranových detektorov môže viesť k získaniu súboru uzatvorených kriviek ktoré vyznačujú hranice objektov, hranice plôch ako aj krivky, ktoré zodpovedajú prerušeniu orientácie povrchu. Takto, uplatnením algoritmov detekcie hrán možno výrazne znížiť množstvo obrazových dát, ktoré majú byť neskôr spracované, a preto môžu odfiltrovať informácie, ktoré môžu byť považované za menej dôležité, pri zachovaní významných štrukturálnych vlastností obrazu. Ak je krok detekcie hrán úspešný, nasledujúca úloha interpretácie obsahu informácií v pôvodnom obraze môže byť podstatne zjednodušená.

Avšak nie vždy je možné získať takto ideálne hrany z obrazov reálneho života strednej zložitosti. Hrany získané z netriviálnych obrazov sú často sprevádzané ich rozdrobenosťou, čo znamená, že krivky hrán bývajú prerušované, chýbajú hrany segmentov ako aj falošné hrany.

Zmeny jasu sa dajú detekovať pomocou prvej a druhej derivácie jasu. Metódy detekcie hrán sú založené na veľkosti prvej derivácie jasu, veľkosti druhej derivácie jasu alebo aj detekcie zmeny znamienka derivácie. Myšlienka použitia derivácií je vysvetlená na obr.1. Na obr.1a je obraz, ktorý obsahuje svetlý pruh na tmavom pozadí, profil jasových úrovní v ktoromkoľvek horizontálnom riadku a prvú a druhú deriváciu uvedeného riadkového profilu. Prechod z tmavej do svetlej úrovne je tu modelovaný ako pozvoľný než ako ostrý, nakoľko takýto prechod odpovedá lepšie reálnym obrázkom.


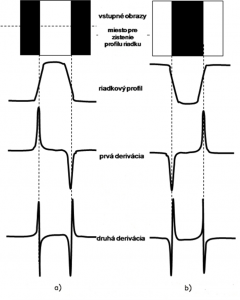
Obr. 1. Prvá a druhá derivácia riadkového profilu pre detekciu hrán

Obr.1 ukazuje, že prvá derivácia riadkového profilu je kladná pri nábežnej hrane prechodu, záporná pri dobežnej hrane a nulová tam kde je úroveň jasu konštantná teda nedochádza k žiadnym jasovým zmenám. Druhá derivácia je kladná pre tie oblasti prechodu, kedy tieto oblasti patria do tmavej strany hrany, záporná pre tie oblasti, ktoré obsahujú svetlú stranu hrany a nula tam kde je úroveň šedej konštantná. Z uvedeného vyplýva, že veľkosť prvej derivácie môže byť použitá na posúdenie, či sa jedná o obrazový bod ležiaci na tmavej alebo svetlej strane hrany. Druhá derivácia má veľmi užitočnú vlastnosť a to, že obsahuje prechody nulou v strede prechodu medzi úrovňami šedi.

Gradientové operátory

Pre funkciu f(x,y) je gradient funkcie f v súradniciach (x,y) definovaná ako vektor

\Delta f = \left [ \begin{array}{c} G_x \\ G_y \end{array} \right ] = \left [ \begin{array}{c} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{array} \right ] (1)

Vektor gradientu má smer najrýchlejšie dosahovanej zmeny f v (x,y). Pri detekcii hrany je veľmi dôležitý modul tohto vektora, všeobecne nazývaný gradient a označovaný \Delta f

\Delta f = |\Delta f | = \left [ G_x^2 + G_y^2 \right ]^{0.5} (2)

Kvôli zjednodušeniu výpočtu je v praxi často používaná aproximácia gradientu pomocou absolútnych hodnôt, ako uvádza nasledovný vzťah,

\Delta f \approx |G_x| + |G_y| (3)

ktorá je oveľa jednoduchšia na implementáciu.

Gradientove metódy

Operátory je možné vyjadriť ako masku pre konvolúciu. Operátory budeme uvádzať pomocou príslušného konvolučného jadra h.

Robertsov operátor je najstarším a veľmi jednoduchým, ktorý používa len okolie 2×2 reprezentatívneho pixlu. Jeho konvolučné masky sú

h_1 = \left [ \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right ]
h_2 = \left [ \begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array} \right ] (4)

Hlavnou nevýhodou Robertsovho operátora je veľká citlivosť na šum, nakoľko je použité malé okolie pre aproximáciu.

Prewittovej operátor aproximuje prvú deriváciu. V okolí 3×3 je odhadovaný gradient pre 8 smerov. Vybraná je maska, ktorá odpovedá najväčšiemu modulu gradientu. Možné je vytvárať i väčšie masky s presnejším smerovým rozlíšením. Uvedieme len prvé 2 konvolučné masky, ostatné vznikajú jednoducho pootočením.

h_1 = \left [ \begin{array}{ccc} 1 & 1 & 1 \\ 0 & 0 & 0 \\ -1 & -1 & -1 \end{array} \right ]
h_2 = \left [ \begin{array}{ccc} 0 & 1 & 1 \\ -1 & 0 & 1 \\ -1 & -1 & 0 \end{array} \right ] (5)

Sobelov operátor okrem vlastnej diferenciácie vykonáva aj isté vyhladzovanie. Nakoľko samotná derivácia zvýrazňuje šum, je efekt vyhladzovania veľmi užitočný. Konvolučné masky vznikajú pootočením

h_1 = \left [ \begin{array}{ccc} 1 & 2 & 1 \\ 0 & 0 & 0 \\ -1 & -2 & -1 \end{array} \right ]
h_2 = \left [ \begin{array}{ccc} 0 & 1 & 2 \\ -1 & 0 & 1 \\ -2 & -1 & 0 \end{array} \right ] (6)

Laplaceov operátor, teda druhá derivácia, predstavuje rýchlosť zmeny hodnôt jasu resp. zmenu zmeny jasu. Prejaví sa najmä na strmých alebo izolovaných hranách alebo ju možno použiť na detekciu izolovaných bodov- bude zvýrazňovať aj šum. Druhú deriváciu v smere x je možné v diskrétnom obraze počítať ako rozdiel rozdielov hodnôt jasu vedľa seba. Na detekciu izolovaných bodov možno použiť tzv. Laplaceov operátor \Delta^2 . Pre Laplaceov operátor sa používajú masky v pozitívnej alebo negatívnej variante

h_1 = \left [ \begin{array}{ccc} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \end{array} \right ]
h_2 = \left [ \begin{array}{ccc} 0 & -1 & 0 \\ -1 & 4 & -1 \\ 0 & -1 & 0 \end{array} \right ] (7)

Spolu s Laplaceovým operátorom sa používa i vyhladzovací Gaussovnský filter. Vtedy hovoríme o Laplaciáne Gaussiánu – LoG. Aproximácia operátora LoG v maske 5×5:

h = \left [ \begin{array}{ccccc} 0 & 0 & -1 & 0 & 0 \\ 0 & -1 & -2 & -1 & 0 \\ -1 & -2 & 16 & -2 & -1 \\ 0 & -1 & -2 & -1 & 0 \\ 0 & 0 & -1 & 0 & 0 \end{array} \right ] (8)

Cannyho hranový detektor realizuje princíp rôzneho rozlíšenia a hľadania najlepšieho z nich. Hlavná myšlienka vychádza z predstavy, že skokovú hranu (v dvojrozmernom obrázku ako schod) môžeme hľadať filtrom. Návrh tohto filtra je formulovaný ako úloha variačného počtu tj. hľadanie najlepšej impulznej funkcie filtra-za podmienky, že budú splnené určité požiadavky na chovanie filtra. Cannyho hranový detektor dnes predstavuje pokročilý hranový detektor.

2. Realizácia a vyhodnotenie algoritmov hranovania šedotónového obrazu

2.1 Realizácia v Matlabe

Algoritmy hranovania šedotónového obrazu boli programovo implementované v programovom prostredí MATLAB. Využité boli funkcie Image Processing Toolbox-u. Hlavnou funkiou je funkia „edge“. V nej sú relizované gradientove metódy a to Sobelova, Prewittovej a Robertsova. Tieto metódy vracajú hranu na tom bode, na ktorom je gradient maximálny.

Ďalšou metódou je pre zero-cross teda prechod cez nulu s použitím filtra Laplacián Gausiánu. Pri tejto metóde je možné definovať SIGMA ako smerodajnú odchýlku filtra Laplacián Gausiánu. V našom prípade bola použitá defaultne sa rovnajúca 2. Veľkosť filtra je vypočítaná pomocou vzťahu CEIL(SIGMA*3)*2+1 , funkcia CEIL zaokrúhľuje na celé čislo. Spomenuté metódy boli pre jednoduchšiu prácu zasadené do grafického užívateľského prostredia.

2.2 Zhodnotenie a porovnanie vlastností realizovaných metód

Na porovnanie realizovaných metód bola vytvorená sada umelých a reálnych obrázkov. V prvom kroku sú metody posudzované subjektívne pomocou absolútneho počtu nájdených hrán, v druhom kroku pomocou vizuálneho zhodnotenia kvality hrán, ich hrúbky, prerušenia, výskytu šumu prípadne deformácie hrán. Umelé obrázky obsahujú jednoduché geometrické tvary a šachovnicu, ktorá simuluje susedstvo rôznych jasových úrovní. Tieto obrázky boli ďalej rozmazané gaussovým filtrom a zašumené bielim šumom s gaussovým rozložením.

Prvým obrázkom ktorým boli metódy porovnané je obr.2. Obrázok predstavuje jednoduché geometrické útvary na ktorých je možné pozorovať správanie sa operátorov- vodorovné a zvislé čiary, ostré rohy, šikmé čiary, kružnica. Obr.3 predstavuje predpokladané hrany, kde uvažujeme, že hrana leží na svetlejšej strane. Nájdené hrany boli spočítané ako počet svetlých pixlov a vynesené do grafu. V grafoch je vyčíslené o koľko percent bolo nájdených viac alebo menej hrán oproti predpokladanému počtu.


Graf.1


Obr.2 Hlavný obrázok.


Obr.3 Predpokladané hrany hlavného obrázku.

Hlavný obrázok. Podľa grafu 1 sa počtu skutočných hrán najviac približuje Prewittovej metóda. Robertsova metóda našla vyšší počet hrán na šikmých a oblých tvaroch. Pri sobelovej,robertsovej a prewittovej metóde sa objavili malé narušeia na rohoch hviezdice, prechod cez nulu a cannyho metóda mierne zaoblovali rohy, kde v prípade cannyho čím bola sigma vačšia tým silnejšie sa prejavovalo zaoblenie. V grafe prvý parameter za canny určuje prah, druhý sigmu.


Graf.2

Obrázok s rozmazaním pomocou gaussovho filtra veľkosti 10×10 a smerodajnou odchýlkou 10. Najviac hrán našla Robertsova metóda čo ukazuje graf.2. Roberts vrátil najhoršie výsledky, trojnásobné hrany, šikmé hrany boli neucelené a rozbité ako aj časť oblých hrán, ostré rohy nenašlo vôbec. Prewitt a Sobel dali lepší výsledok, objavili sa dvojité hrany, nenájdené ostré rohy. Prechod cez nulu zaoblil rohy a ostré rohy nenašiel vôbec. Najlepšie dopadol Canny, ktorý dal pekné ucelené hrany, no rohy zaoblil a ostré rohy neuzavrel celkom.




Graf.3

Hlavný obrázok zašumený bielym šumom so strednou hodnotou 0.01 a odchýlkou 0.01. Najviac hrán našiel prechod cez 0 a canny_0.01_2. Prechod cez 0 nie je odolný voči šumu čo sa aj ukázalo. Sobel a Prewitt sa ukázali najodolnejšie voči šumu vodorovné a zvislé hrany boli však „zubaté“. Roberts našiel niekoľko hrán zo šumu no vodorovné a zvislé čiary boli rovné. Canny po úprave hodnoty prahu sa zbavil šumových hrán no rovné čiary boli mierne „zubaté“.


Obr.4 Šachovnica

V ďalšej fáze boli metódy odskúšané a porovnané na umelo vytvorenej šachovnici, ktorá simuluje susedstvo rôznych jasových úrovní.


Graf.4

Šachovnica. Graf.4 ukazuje, že výrazne menej hrán bolo nájdených Sobelom, Prewittom a Robertsom. Hrany neboli nájdené pri rozdiely jasu veľkosti 20 a 40 okrem Robertsa, ktorý rozdiel jasu veľkosti 40 našiel. Prechod cez nulu našiel všetky hrany, avšak objavili sa hrany dvojité pri jasovom rozdiely 100 a 120, niektoré rohy neboli uzavreté. Canny našiel všetky hrany, rohy však neuzatváral prípadne mierne zaoblil.


Graf.5

Šachovnica s rozmazaním pomocou gaussovho filtra veľkosti 5×5 a smerodajnou odchýlkou 5. Podľa grafu.5 Sobel, Prewitt a Roberts nenašli hrany ktorých jasový rozdiel bol 40 a menší. Prechod cez nulu dal veľmi dobré výsledky, našiel všetky hrany, niektoré rohy však neuzavrel. Canny takisto našiel všetky hrany, niektoré rohy neuzavrel, prípadne zaoblil.




Graf.6

Šachovnica zašumená bielym šumom so strednou hodnotou 0.01 a odchýlkou 0.01. Graf.6 ukazuje, že vo všeobecnosti všetky metódy dali veľmi zlé výsledky. Najhoršie dopadol prechod cez nulu ktorý mnoho hrán nenašiel a našiel veľké množstvo falošných šumových hrán. Sobel, Prewitt a Roberts niektoré hrany nenašli, ale objavilo sa mnoho šumových hrán. Najlepšie dopadol Canny s úrovňou prahu 0.2. Vtedy sa odfiltrovali šumové hrany, no došlo k strate niektorých skutočných hrán.

V poslednej fáze boli všetky metódy odskúšané a porovnané na reálnych obrazoch, obr.5, obr.6 a obr.7 . Obrázok 5 predstavuje dopravné značky odfotené kompaktným fotoaparátom pri rôznych svetelných a fyzikálnych (roztrasenie) podmienkach. Obrázok 6 predstavuje štátnu poznávaciu značku z motocykla osvetlenú priamym slnkom a neosvetlenú v tieni. Tretí obrázok 7 predstavuje portrét modelky.

Dopravné značky. Najslabší výsledok dali Sobel, Prewitt, Roberts. Pri značkách so slabými svetelnými podmienkamy nenašli hlavné črty značky. Prechod cez nulu pri slabom svetle takisto nenašiel hrany, v ostatných prípadoch však dal lepší výsledok ako predchádzajúce metódy. Najlepšie dopadol Canny, ktorý našiel aspoň čiastočne hrany aj v slabom svetle.


Obr.5 Dopravné značky

Poznávacie značky. Sobel, Prewitt a Roberts dali veľmi slušné výsledky. V prípade nepriamo osvetlenej značky dali čisté a jasné obrysy čísel a písmen, na priamo osvetlenej značke problémy spôsobili ostré odrazy svetla, poradili si však s trblietavým povrchom značky, nie však dokonale. Prechod cez nulu mal problém s trblietavým povrchom ktorý spôsobil nájdenie falošných hrán, na nesvetlenej značke našiel niekoľko dvojitých hrán. Najlepšie dopadol Canny pre vhodne zvolené parametre prahu a sigmy. Na osvetlenej značke sa nenašli žiadne šumové hrany a len málo dvojitých, na neosvetlenej našlo hrany písmen a čísel veľmi dobre.


Obr.6 Poznávacie značky

Modelka. V prípade obrázku modelky je i subjektívne veľmi náročné zhodnotiť výsledky metód. Vo všeobecnosti však všetky metódy našli obrys postavy, a niektoré črty tváre ako nos, oči a ústa. Najmenej týchto črtov našiel Canny s prahom 0.2 a sigmou 3.6. Črty tváre najlepšie našiel Sobel.


Obr.7 Modelka


Obr.8 Canny


Obr.9 Prewitt


Obr.10 Roberts


Obr.11 Robinson


Obr.12 Sobel


Obr.13 Zero Cross

3. Zhrnutie

Na porovnanie a vyhodnotenie metód detekcie hrán je nedostatok objektívnych kritérií. Jednotlivé metódy boli hodnotené subjektívne a to spočítaním nájdených hrán a slovným zhodnotením kvality nájdených hrán. Nie je možné jednoznačne určiť ktorá metóda je najefektívnejšia. Možno však zhrnúť, že metóda prechodu cez nulu nie je odolná voči šumu v čom bol i teoretický predpoklad. Robertsova, Prewittovej a Sobelova metóda bola do istej miery odolná voči šumu.

V prípade Cannyho metódy na výsledok mala vplyv hodnota sigma ako aj úroveň prahu, ktorý síce odstránil šumové hrany, ale nastala i strata skutočných hrán. Cannyho metóda tiež do značnej miery zaobľovala rohy- čím väčšia sigma, tým väčšie zaoblenie, čo môže byť pri niektorých aplikáciách považované za nežiaducu vlastnosť. Na reálnych obrázkoch bolo možné pozorovať vlastnosti nájdené na umelých obrázkoch.

Použitá literatúra

  1. KLÍMA,M.-BERNAS.M-HOZMAN.J-DVOŘÁK.P.1999. Zpracování obrazové informace. Praha: Vydavatelství ČVUT, 1999. 177s. ISBN-80-01-01-01436-3
  2. HLAVÁČ.Š-SEDLÁČEK.M.2001. Zpracování signálů a obrazů. 1.vyd.Praha: Vydavatelství ČVUT, 2001. 220s. ISBN- 80-01-02114-9
  3. ŠONKA.M-HLAVÁČ.V.1992. Počítačové vidění. 1 vyd.Praha : Grada Publishing, 1992. 272s. ISBN 80-85424-67-3.
  4. Dobeš.M.2008. Zpracování obrazu a algoritmy v C# 1.vyd.Praha : BEN – technická literatura, 2008. 144s. ISBN-978-80-7300-233-6.
  5. Sonka, M., Hlavac, V., Boyle, R.: Image Processing, Analysis, and Machine Vision. Brooks/Cole Publisihing Company, Pacific Grove, USA, 1998. 256s. ISBN 0-534-95393-X
Spoluautorom článku je Rudolf Ravas, Katedra merania, FEI STU, 812 19 Bratislava, Slovenská republika
Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Meracia technika, ISBN 978-80-227-3508-7

Napísať príspevok