Problém rozhodovania s neistými dátami

15. August, 2011, Autor článku: Ladovský Tomáš, Informačné technológie
Ročník 4, číslo 8 Pridať príspevok

Článok sa snaží prezentovať problém rozhodovania s neistými dátami. Tvorca rozhodnutí má k dispozícií namerané minulé realizácie, pomocou ktorých je schopný urobiť predikciu do budúcnosti. Článok najskôr rieši jednoduchý rozhodovací problém v reálnej aritmetike a zaoberá sa optimálnou voľbou metódy odhadu. Postupne pridáva neistú informáciu, pomocou ktorej chceme predpovedať presnejšie realizácie časov spracovania. Prvé neisté časy spracovania modeluje článok pomocou intervalovej aritmetiky.

Tá so sebou prináša problematiku ich odhadu a porovnania. Navyše intervaly nedokážu modelovať informáciu o početnosti minulých realizovaných hodnôt. A tak prechádzame z intervalovej aritmetiky do fuzzy aritmetiky. Tá zo sebou prináša taktiež problematiku odhadu a porovnania fuzzy čísel.

1. Motivačný príklad

Predstavme si nasledujúci rozvrhovací (rozhodovací) problém. K dispozícií máme tri stroje (procesory) M₁, M₂ a M₃, ktoré majú spracovať porade úlohy J₁, J₂ a J₃, čo znamená, že úloha J₁ bude spracovaná na stroji M₁, úloh J₂ bude spracovaná na stroji M₂ a úloha J₃ bude spracovaná na stroji M₃. Časy spracovania úloh J₁, J₂ a J₃ sú porade p₁, p₂ a p₃.

Obr. 1: Obrázok zobrazuje výpočet kumulovaných pracovných časov L₁, L₂ a L₃ na strojoch porade M₁, M₂ a M₃ vzhľadom na rozhodnutia tvorcu rozvrhu, t.j. $x\in\{1,2,3\}$

Našou úlohou je rozhodnúť, ktorému stroju pridelíme úlohu J₄ s časom spracovania p₄, tak aby sme čo najviac zrovnomernili záťaž na všetkých troch strojoch. V tomto okamihu rozhodovania (plánovania) ešte nevieme aké skutočné časy spracovania sa budú realizovať. Poznáme časy spracovania minulých nameraných realizácií úloh alebo iba ich odhady. Na obrázku 1 môžeme vidieť pseudokód našeho rozhodovacieho problému. Záťaž na i-tom stroji M_i zapisujeme ako L_i.

Celočíselná premenná $x\in\{1,2,3\}$ modeluje rozhodnutie tvorcu rozvrhu, či buď bude spracovaná úloha J₄ na prvom stroji (x=1), alebo či bude úloha J₄ spracovaná na druhom stroji (x=2), alebo či bude úloha J₄ spracovaná na treťom stroji (x=3). Existuje viacero optimalizačných kritérií, ktoré sú známe pod pojmom miera nerovnomernosti alebo Schur konvexná funkcia. Čím je miera nerovnomernosti menšia, tým je zaťaženie strojov rovnomernejšie. Pre náš účel nám poslúži miera nerovnomernosti definovaná ako

$f_{dif}(x_1,x_2,x_3) = \max\{x_1,x_2,x_3\} - \min\{x_1,x_2,x_3\},$

kde x₁, x₂, x₃ nepredstavujú jednotlivé rozhodnutia tvorcu rozvrhu, ale predstavujú zaťaženia strojov M₁, M₂, M₃.

Poznámka: Časy spracovania úloh sú nezávislé od stroja na ktorom sú úlohy spracované.

Príklad 1.1. (Pracovné časy modelované reálnymi hodnotami)

Máme k dispozícií súbor dát za predošlé obdobie, viď. tabuľka.

i-te meranie	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
$p_{1i}^*$	4	3	14	7	8	6	3	8	1	7	15	11	6	8	9
$p_{2i}^*$	11	10	3	14	7	6	12	2	5	3	9	7	4	9	9
$p_{3i}^*$	11	9	3	13	7	7	3	3	9	10	10	11	4	4	10
$p_{4i}^*$	2	3	7	2	7	15	9	10	9	6	5	15	9	12	10

Ide o namerané (skutočné) hodnoty časov spracovania úloh J₁, J₂, J₃ a J₄. Aj keď ide o úlohy rovnakého typu, tak nám merania ukázali, že ich časy spracovania sú rôzne od naplánovaných pôvodných časov. Tieto výchylky sú spôsobené ľudským faktorom, poruchami strojov a nečakanými udalosťami. Z týchto dát vieme určiť približné hodnoty (odhady) časov spracovania p₁, p₂, p₃ a p₄. Existuje viacero spôsobov ako tieto odhady vypočítať:

aritmetický priemer
modus
medián
optimistická hodnota (minimum)
pesimistická hodnota (maximum)

Za predpokladu, že chceme narábať s presnými číslami a nechceme si komplikovať optimalizáciu zavádzaním neistých údajov, môžeme odhadované časy spracovania úloh J₁, J₂, J₃ a J₄ určiť pomocou aritmetického priemeru. Teda pre prvú úlohu vypočítame čas spracovania ako $p_1 = \frac{1}{N}\sum_{i\in N}p^*_{1i}$ , kde N je veľkosť súboru. Podobne počítame časy spracovania pre druhú, tretiu a štvrtú úlohu. Teda môžeme písať:

$p_1 = 7.33,\quad p_2 = 7.40,\quad p_3 = 7.60\quad\text{a}\quad p_4 = 8.07$

Najskôr skúsime priradiť úlohu J₄ prvému stroju M₁, (x=1), a získame nasledujúce zaťaženia strojov L₁ = 7.33 + 8.07 = 15.40, L₂ = 7.40 a L₃ = 7.60. Teraz skúsime priradiť úlohu J₄ druhému stroju M₂, (x=2), pre toto rozhodnutie obdržíme nasledujúce zaťaženia strojov L₁ = 7.33, L₂ = 15.47 a L₃ = 7.60. Poslednou možnosťou je priradiť štvrtú úlohu tretiemu stroju M₃, (x=3), obdržíme nasledujúce zaťaženia strojov L₁ = 7.33, L₂ = 7.40 a L₃ = 15.67. Pre prvú variantu, (x=1), je miera nerovnomernosti rovná hodnote f⁽¹⁾_dif(L₁,L₂,L₃) = L₁ – L₂ = 15.40 – 7.40 = 8.0. Pre druhú variantu, (x=2), je miera nerovnomernosti rovná hodnote f⁽²⁾_dif(L₁,L₂,L₃) = L₂ – L₁ = 15.47 – 7.33 = 8.14. A pre tretiu variantu, (x=3), je miera nerovnomernosti rovná hodnote $latex f⁽³⁾_dif(L₁,L₂,L₃) = L₃ – L₁ = 15.67 – 7.33 = 8.34. V úvode sme povedali, že čím je miera nerovnomernosti menšia, tým sú zaťaženia strojov rovnomernejšie. Preto by sa tvorca rozvrhu rozhodol pre prvú variantu.

Je možné, že pri voľbe inej metódy odhadu časov spracovania by sme obdržali iný výsledok. Napríklad pri voľbe modusu ako metódy odhadu časov spracovania by sa tvorca rozvrhu rozhodol pre tretiu variantu. Výber metódy odhadu je dôležitou súčasťou optimalizačného problému. Tvorca rozvrhu môže mať napríklad za úlohu vypočítať optimistický rozvrh, čo najviac realistický rozvrh alebo pesimistický rozvrh.

Pri tvorbe optimistického rozvrhu môžu tvorcu rozvrhu zaujímať minimálne namerané hodnoty, z ktorých vytvorí odhad. Pri pesimistickom rozvrhu môže tvorcu rozvrhu zaujímať maximálna hodnota, ktorú obsahuje súbor nameraných časov spracovania. Takáto tvorba rozvrhov môže dopomôcť riadeniu sa napríklad finančne pripraviť na prichádzajúce obdobie. Pri tvorbe čo najviac realistického rozvrhu potrebujeme poznať čo najviac informácií. Jednou z možností je modelovať časy spracovania pomocou reálnych intervalov.

2. Intervalová aritmetika

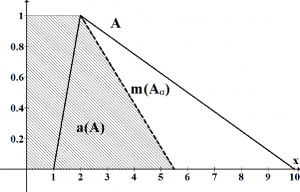
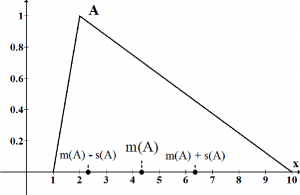
Interval je definovaný [2] ako $A = [a_L,a_R] = \{ t\,|\, a_L\leq t\leq a_R, t\in\mathfrak R\}$ , kde a_L, a_R sú porade ľavý a pravý okraj intervalu A definovaného na reálnych číslach. Ak a_L = a_R = a, potom A = [a,a] je reálne číslo. Interval A môžeme alternatívne reprezentovať pomocou jeho stredu m(A) a polovicou jeho šírky (alebo jednoducho šírkou) w(A) ako A = <m(A),w(A)>, kde m(A) = (a_L+a_R)/2 a w(A) = (a_R-a_L)/2.

V literatúre sa na m(A) taktiež odkazujeme ako na priemernú hodnotu, centrálnu hodnotu alebo očakávanú hodnotu intervalu A (Ishibuchi & Tanaka 1990). Podobne alternatívami w(A) sú rozsah, miera neistoty, rozsah neistoty alebo jednoducho neistota intervalu A. Na ľavý okraj a pravý okraj intervalu A sa zvykne odkazovať ako na spodnú a hornú hranicu, minimálnu a maximálnu hodnotu alebo ako na infimum a suprémum. Okada & Gen 1994 použili názvy ako pesimistická a optimistická hodnota intervalu A. Dva intervaly A a B sa:

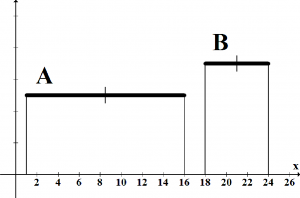
Neprekrývajú (sú disjunktné), t.j. a_R < b_L, obrázok 2(a).
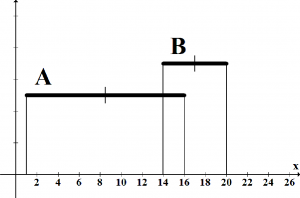
Čiastočne prekrývajú, t.j. a_L < b_L ≤ a_R < b_R, obrázok 2(b).
Úplne prekrývajúce, také že B ⊆ A, obrázky 2(c), 2(d) a 2(e).

(a) Neprekrývajúce sa intervaly

(b) Čiastočne sa prekrývajúce intervaly

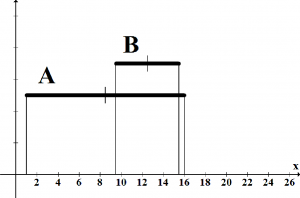
(c) Úplne sa prekrývajúce intervaly m(A) < m(B)

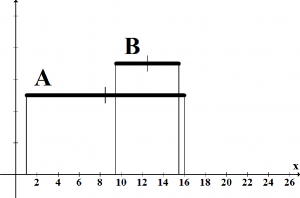
(d) Úplne sa prekrývajúce intervaly m(A) = m(B)

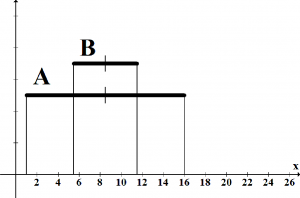
(e) Úplne sa prekrývajúce intervaly m(A) > m(B)

Obr. 2: Obrázok zobrazuje 5 spôsobov ako sa môžu prekrývať intervalové čísla.

Príklad 2.1. (Pracovné časy modelované reálnymi intervalmi)

Použijeme rovnaký tréningový súbor ako v predchádzajúcom príklade, ale budeme predpokladať, že tvorcu rozvrhu nezaujímajú početnosti s akými sa jednotlivé časy spracovania úloh udiali², ale že ho skôr zaujíma rozsah hodnôt, ktoré sa realizovali. Ani v tomto prípade si optimalizáciu nechce príliš komplikovať a preto predpokladá, že sa tieto realizácie časov spracovania realizujú rovnomerne. Na takéto modelovanie rozsahu hodnôt, pričom každá hodnota sa môže realizovať s rovnakou pravdepodobnosťou, sa hodia reálne intervaly. Aj v tomto prípade záleží na tvorcovi rozvrhu, akú metódu odhadu časov spracovania zvolí:

min – max
min – modus, modus – max
min – medián, medián – max

My použijeme jednoduchý odhad min-max, kde ľavá hodnota času spracovania úlohy J₁ je minimum z nameraných časov spracovania a pravá hodnota času spracovania úlohy J₁ je maximum z nameraných časov spracovania, t.j. $p_1 = [\min_{i\in N}\{p^*_{1i}\}, \max_{i\in N}\{p^*_{1i}\}]$ . Teda môžeme písať

$p_1 = [1,15],\quad p_2 = [2,14],\quad p_3 = [3,13]\quad\text{a}\quad p_4 = [2,15]$

Podobne ako v predchádzajúcom príklade je prvou variantou, (x=1), čo znamená, že úlohu J₄ pridelíme prvému stroju. Získame tak zaťaženia strojov, ktoré sú porade rovné hodnotám L₁ = [3,30], L₂ = [2,14] a L₃ = [3,13]. Druhou variantou je priradenie úlohy J₄ stroju druhému, (x=2). Ne základe tohoto rozhodnutia vieme spočítať zaťaženia strojov, ktoré sú porade L₁ = [1,15], L₂ = [4,29] a L₃ = [3,13]. Treťou variantou je, že priradíme úlohu J₄ tretiemu stroju, (x=3), obdržíme tak nasledujúce zaťaženia strojov L₁ = [1,15], L₂ = [2,14] a L₃ = [5,28]. Teraz nám treba spočítať mieru nerovnomernosti, ktorá je definovaná ako

$f_{dif}(L_1,L_2,L_3) = \max\{L_1,L_2,L_3\} - \min\{L_1,L_2,L_3\}$

Teda od väčšieho zaťaženia odčítame menšie zaťaženie. Ako vidíme, nie je úplne jednoznačné, či pre druhú variantu, (x=2), je zaťaženie na prvom stroji väčšie ako zaťaženie na stroji treťom. Táto neistota je spôsobená úplným prekrytím intervalov. V dnešnej dobe existuje niekoľko metód, ktoré nám majú pomôcť s touto problematikou, no o každej z nich treba vedieť, prečo práve zvolenú metódu chceme použiť a ako nám jej voľba ovplyvní výsledok. Náš príklad nie je nejako zložitý, a preto si vyberieme metódu porovnania podľa centrálnej hodnoty. Pre prvú variantu, (x=1), môžeme písať, m(L₁) = 8, m(L₂) = 16.5 a m(L₃) = 8. Vidíme, že centrálna hodnota pre druhé zaťaženie L₂ je väčšia ako centrálne hodnoty pre zaťaženia L₁ a L₃. Teda našli sme maximálne zaťaženie strojov. Teraz ešte potrebujeme nájsť minimálne zaťaženie strojov.

Keď porovnáme centrálne hodnoty zaťažení strojov L₁ a L₃, tak zistíme, že sú rovnaké. V takomto prípade môžeme porovnať šírky ich kumulovaných časov spracovania. Pre L₁ a L₃ môžeme písať, že w(L₁) = 7 a w(L₃) = 5. Tu tvorca rozvrhu narazí na ďalší problém. Podľa čoho sa tvorca rozvrhu rozhodne, ktorá z týchto dvoch hodnôt je pri minimalizácii viac preferovaná? Predpokladajme, že tvorca rozvrhu má za úlohu vytvoriť optimistický rozvrh, v ktorom sú preferované zaťaženia strojov s menšou šírkou. Preferovanie intervalu menšej šírky pri minimalizačnej optimalizácii znamená, že tvorca rozvrhu počíta s tým, že budúce realizácie časov spracovania úloh sa budú realizovať v okolí centrálnej hodnoty plánovaných časov spracovania. Pri takomto predpoklade tvorca rozvrhu zvolí za minimálne zaťaženie L₃ a miera nerovnomernosti je rovná hodnote

$f^{(2)}_{dif}(L_1,L_2,L_3) = L_2 - L_3 = [4,29] - [3,13] = [-9,26]$

Podobne pre prvú variantu, (x=1), môžeme písať, m(L₁) = 16.5, m(L₂) = 8 a m(L₃) = 8 a w(L₂) = 6, w(L₃) = 5. V tomto prípade je zaťaženie na prvom stroji maximálne a minimálne na stroji treťom. Z tohoto dôvodu je miera nerovnomernosti pre prvú variantu rovná hodnote

$f^{(1)}_{dif}(L_1,L_2,L_3) = L_1 - L_3 = [3,30] - [3,13] = [-10,27]$

Pre tretiu variantu, (x=3), môžeme písať, m(L₁) = 8, m(L₂) = 8 a m(L₃) = 16.5 a w(L₁) = 7, w(L₂) = 6. Miera nerovnomernosti pre tretiu variantu je rovná hodnote

$f^{(3)}_{dif}(L_1,L_2,L_3) = L_3 - L_2 = [5,28] - [2,14] = [-9,26]$

Teraz nám treba vybrať optimálnu variantu, čo znamená nájsť minimálnu mieru nerovnomernosti. Pre miery nerovnomernosti môžeme písať, že ich centrálne hodnoty sú rovné

$m(f^{(1)}_{dif}) = m(f^{(2)}_{dif}) = m(f^{(3)}_{dif}) = 8.5$

Pre ich šírky platí

$w(f^{(1)}_{dif}) = 18.5\quad\text{ a }\quad w(f^{(2)}_{dif}) = w(f^{(3)}_{dif}) = 17.5$

Aj v tomto prípade charakterizuje lepší rozvrh menšia šírka (ľavá aj pravá hodnota miery nerovnomernosti je bližšie k nule). Preto tvorca rozvrhu vyberie za optimálny druhý (tretí) variant.

Vidíme, že voľba maximálneho a minimálneho zaťaženia pri výpočte miery nerovnomernosti nie je úplne jednoznačná. Táto voľba je sprevádzaná neistotou. Dôvodmi tejto neistoty sú, že nepoznáme všetky kritéria optimalizácie rozhodovacieho problému. Napríklad, či považujeme pri minimalizačnej optimalizácii interval s menšou šírkou za viac preferovaný (menší – optimistický rozvrh) alebo či považujeme interval s väčšou šírkou za viac preferovaný (pesimistický rozvrh).

Ďalej si môžeme všimnúť, že sa zmenilo rozhodnutie tvorcu rozvrhu o výbere optimálneho variantu. V prvom príklade sa rozhodol tvorca rozvrhu pre výber prvej varianty. V tomto príklade sa ale tvorca rozvrhu rozhodol pre výber druhej alebo tretej varianty. Čo to znamená? V prvom príklade sme modelovali pracovné časy pomocou reálnych hodnôt, ktorých odhady sme robili pomocou aritmetického priemeru. V tomto príklade sme modelovali pracovné časy pomocou reálnych intervalov, ktorých odhad sme robili za pomocou min-max princípu a porovnávali sme ich pomocou centrálnej hodnoty a šírky.

Je teda zrejmé, že oba modely sú veľmi citlivé vzhľadom na výber typu modelovania časov spracovania, odhadov časov spracovania a ich porovnania. O tom ktorý rozvrh je optimálnejší rozhodne až skutočná realizácia časov spracovania. No ani pri nej nie je isté, či by rozvrh vypracovaný vzhľadom na takéto dopredu známe časy spracovania viedol na ich opätovnú realizáciu.

Okrem porovnania intervalov pomocou strednej hodnoty a šírky intervalu A, spomenieme ešte dve metódy porovnania. Prvou je metóda používajúca pravdepodobnostný prístup. Nakahara a kol. (1992) definovali pravdepodobnosť nerovnice P(A≤B) pre ľubovoľné dva intervaly A = [a_L,a_R] a B = [b_L, b_R] ako P(A≤B) = P(a≤b), kde a a b sú náhodné premenné rovnomerne rozložené na A a B a P(a ≤ b) je pravdepodobnosť, že a≤b. Nakahara a kol. (1992) študoval pravdepodobnosť, že A≤B pre šesť rôznych pozícií intervalov A a B na reálnej osi, a) a_L≤a_R≤b_L≤b_R, b) a_L≤b_L≤a_R≤b_R, c) a_L≤b_L≤b_R≤a_R, d) b_L≤a_L≤a_R≤b_R e) b_L≤a_L≤b_R≤a_R a f) b_L≤b_R≤a_L≤a_R a definoval pravdepodobnostnú hodnotu pre všetkých šesť prípadov vo všeobecnej forme ako

$P(A\leq B) = \frac{w-a_L}{a_R-a_L} + \frac{v-w}{(a_R-a_L)(b_R-b_L)} (b_R-\frac{v+w}{2})$

kde

$w = \min\{\max\{a_L,b_L\},a_R\}\quad\text{ a }\quad v = \max\{ \min\{ a_R,b_R \}, a_L \}$

Poznámka 1. (Nakaharovo pravdepodobnostné porovnanie intervalov)

Ak P(A≤B) = 0.5 potom A a B sú úplne sa prekrývajúce intervaly. Nevieme rozhodnúť, ktorý je väčší alebo menší. Tu nám pomôže porovnať intervaly A a B podľa šírky.

Inou metódou porovnania intervalov je index prijateľnosti (Sengupta a kol. 2009), ktorý definujeme: Nech I je množina všetkých intervalov definovaných na množine reálnych čísel $\mathfrak R$ . Index prijateľnosti $A: I\times I\rightarrow [0,\infty )$ definujeme ako

$A(A \prec B) = \frac{m(B) - m(A)}{w(B) + w(B)}$

kde $w(B) + w(A) \neq 0$ . $A(A\prec B)$ môžeme interpretovať ako stupeň prijateľnosti, že prvý interval je inferiórny k druhému intervalu. Stupeň prijateľnosti $A(A\prec B)$ môžeme klasifikovať a ďalej interpretovať na základe porovnania pozície stredu a šírky intervalu B s rešpektom na interval A ako

$A(A\prec B) \left\{ \begin{array}{cc} = 0 & \text{ak}\quad m(A) = m(B) \\ \in (0,1) & \text{ak}\quad m(A) < m(B)\text{ a } a_R > b_L \\ \geq 1 & \text{ak}\quad m(A) < m(B)\text{ a } a_R \leq b_L \end{array} \right .[/latex]</td> <td style="width:20px; text-align:center;"></td> </tr> </table> <p align="justify">Klasifikáciu stupňov prijateľnosti interpretujeme nasledujúco: <ul> <li>Ak <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />A(A \prec B) = 0$ , potom tvrdenie “A je inferiórne k B” neakceptujeme.

Ak $0 < A(A \prec B) < 1[/latex], potom tvorca rozhodnutí prijíma tvrdenie "A je inferiórne k B" so stupňom prijateľnosti [latex]A(A \prec B)[/latex]</li> <li>Ak <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />A(A \prec B)\geq 0$ , potom je tvorca rozhodnutí absolútne spokojný s tvrdením “A je inferiórne k B”, alebo inými slovami, považuje tvrdenie za pravdivé.

V tejto sekcii sme modelovali časy spracovania úloh pomocou reálnych intervalov. Odhady časov spracovania sme robili na základe min-max metódy, čo znamená, že za ľavú hodnotu intervalu sme zvolili minimálnu hodnotu a za pravú hodnotu sme zvolili maximálnu hodnotu z nameraných dát. Tak ako aj v predošlom príklade je voľba metódy odhadu časov spracovania kľúčom k dobrému modelu a dôveryhodným výsledkom. Ďalej sme v príklade aplikovali lexikografickú metódu porovnania intervalov a to podľa stredu a šírky. Taktiež voľba vhodnej metódy porovnania intervalov je kľúčovou. Rozhoduje o tom, ktorému stroju priradíme úlohu J₄ a taktiež rozhoduje o tom, ktorý variant zvolíme za optimálny.

V prvom príklade sme používali na modelovanie časov spracovania úloh reálne hodnoty. Do intervalovej aritmetiky sme prešli z dôvodu nevyužitia informácie, ktorou disponuje súbor nameraných a uskutočnených časov spracovania úloh. Oproti reálnym odhadom časov spracovania úloh nám intervalová aritmetika dovoľuje modelovať krajné a vnútorné realizácie časov spracovania. Nevýhodou intervalovej aritmetiky je, že nemodeluje početnosti jednotlivých realizácií časov spracovania, čo do určitej miery sme mohli modelovať aritmetickým priemerom v reálnych číslach. Zaujímavou otázkou je ako dostať túto informáciu do intervalovej aritmetiky.

Ponúkajú sa dve možnosti. Jednou je modelovať informáciu zo súboru nameraných časov spracovania pomocou pravdepodobnostného rozdelenia. Druhou a jednoduchšou možnosťou je modelovať budúce realizácie časov spracovania pomocou fuzzy čísel. Nasledujúca sekcia sa venuje ľahšej možnosti a modeluje očakávané časy spracovania úloh J₁, J₂, J₃ a J₄ trojuholníkovými fuzzy číslami, ktoré sa snažíme čo najpresnejšie aproximovať na dané realizácie časov spracovania. Inými možnosťami je voliť tvar a funkciu príslušnosti fuzzy čísla podľa skúseností. V predošlom príklade sme sa stretli s problémom porovnania intervalov. Inak to nebude ani s porovnaním fuzzy čísel s tým rozdielom, že sa teraz budeme snažiť porovnať omnoho komplexnejšiu informáciu.

3. Fuzzy aritmetika

Nech $\mathfrak R$ je množina reálnych čísel. Fuzzy množinu A definujeme na $\mathfrak R$ pomocou funkcie príslušnosti $\mu_A:\mathfrak R\rightarrow [0,1]$ , kde $\mu_A(x)$ predstavuje stupeň príslušnosti elementu x vo fuzzy množine A. Fuzzy podmnožina A definovaná na $\mathfrak R$ je normálna, ak a iba ak $H(A) = \sup_{x\in \mathfrak R}\{\mu_A(x)\} = 1$ , kde H(A) je výška fuzzy množiny A. Fuzzy podmnožina A množiny $\mathfrak R$ je konvexná, ak a iba ak $\mu_A(\lambda x+(1-\lambda)y)\geq\min\{\mu_A(x),\mu_A(y)\}$ , kde $x,y\in\mathfrak R$ a $\lambda\in [0,1]$ . Nosič množiny A je definovaný ako $S(A) = \{x\,|\, \mu_A(x) > 0\}$ . Fuzzy množina A sa nazýva fuzzy číslo, ak a iba ak A je normálna, konvexná a nosič množiny A je ohraničený na $\mathfrak R$ . Trojuholníkové fuzzy číslo A je fuzzy číslom so spojitou lineárnou funkciou príslušnosti $\mu_A(x)$ definovanou ako:

$\mu_A(x) = \left\{ \begin{array}{cc} \mathcal (x-a)/(b-a) & \text{pre} a\leq x\leq b, \\ \mathcal (c-x)/(c-b) & \text{pre} b\leq x\leq c, \\ 0 & \text{inak} \end{array} \right .$

V nasledujúcom texte používame namiesto pojmu trojuholníkové fuzzy číslo skrátený tvar fuzzy číslo. Fuzzy číslo môžeme taktiež značiť ako usporiadanú trojicu A = (a,b,c), kde $a\leq b\leq c$ a $a,b,c\in\mathfrak R$ . Hodnota a je nazývaná infimom, b je nazývaná modusom a c je nazývaná suprémom. Taktiež sa používajú označenia pre a ako ľavá hodnota, spodná hodnota, pre b sa používajú označenia ako centrálna hodnota, stredná hodnota a pre c sa používajú označenia ako pravá hodnota, horná hodnota. V nasledujúcom texte sa obmedzíme na také trojuholníkové fuzzy čísla, ktorých hodnoty usporiadanej trojice sa nerovnajú. Definujme množinu všetkých fuzzy čísel s prirodzenými hodnotami a,b,c ako

$\mathcal H(N) = \{(a,b,c)\,|\,a < b < c,\, a,b,c\in N_0\}[/latex]</td> <td style="width:20px; text-align:center;"></td> </tr> </table> <p align="justify">Označme reálny interval <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />A_\alpha$ ako $\alpha$ -rez fuzzy množiny A a definujme ho ako

$A_\alpha = [a^L_\alpha,a^R_\alpha] = [a+(b-a)\alpha,c+(b-c)\alpha]$

Nech $m(A_\alpha)$ je centrálna hodnota elementov $\alpha$ -rezu, ktorú pre fuzzy číslo A = (a,b,c) spočítame ako

$m(A_\alpha) = m[a^L_\alpha,a^R_\alpha] = ((2b-a-c)\alpha + (a+c))/2,$

kde $\alpha\in[0,1]$ . Nech A je ľubovoľné fuzzy číslo A = (a,b,c), potom obsah plochy a(A) pod grafom $m(A_\alpha)$ (viď. obrázok 3(a)) spočítame pre $\alpha\in[0,1]$ ako

$a(A) = \int_0^1 m[a^L_\alpha,a^R_\alpha]\,d\alpha = (a+2b+c)/4$

Strednú hodnotu fuzzy čísla A spočítame ako

$m(A) = (a+b+c)/3$

smerodajnú odchýlku fuzzy čísla A spočítame ako

$s(A) = \sqrt{a^2+b^2+c^2-ab-bc-ac}/(3\sqrt{2})$

Ukážku strednej hodnoty a smerodajnej odchýlky fuzzy čísla A môžeme vidieť na obrázku 3(b).

Ukážka obsahu ohraničeného funkciou $m(A_\alpha)$ a x-ovou osou

Ukážka strednej hodnoty a smerodajnej odchýlky fuzzy čísla A

Obr.3 Na ľavom obrázku (a) môžeme vidieť obsah oblasti ohraničenej funkciou $m(A_\alpha)$ a x-ovou osou. Pravý obrázok (b) zobrazuje strednú hodnotu a smerodajnú odchýlku fuzzy čúsla A

Chen a Chen v roku 2003 odvodili metódu porovnania fuzzy čísel, založenú na súradniciach ťažiska $T=(\hat{x},\hat{y})$ fuzzy čísla a smerodajnej odchýlke s(A). Chen a Chenov index porovnania pre fuzzy čísla A=(a,b,c) je definované ako $F^{(1)}(A) = \hat{x}_A + (1-\hat{y}_A)^{s(A)}$ , kde horizontálna súradnica je rovná hodnote $\hat{x}_A=(2b\hat{y}_A+(c+a)(1-\hat{y}_A))/2$ a vertikálna súradnica je rovná hodnote $\hat{y}_A = 1/3$ . Čím je hodnota $F^{(1)}(A)$ väčšia, tým je fuzzy číslo väčšie.

Nedostatkom jednokritériálnych porovnávacích indexov je strata informácie. Taktiež jednokritériálne indexy porovnania považuje veľkú množinu rôznych fuzzy čísel za rovnaké. Z tohoto dôvodu sa používajú multikriteriálne optimalizačné techniky ako lexikografický prístup. V lexikografickom prístupe sa rozhoduje podľa viacerých kritérií.

McCahon a Lee [1] stanovili dve kritéria $F^{(2)}_1(A) = m(A)$ a $F^{(2)}_2(A) = s(A)$ . Väčšie z dvoch fuzzy čísiel je to, ktoré má väčšiu strednú hodnotu $F^{(2)}_1$ , v prípade zhody stredných hodnôt je väčšie to s väčšou smerodajnou odchýlkou $F^{(2)}_2$ , a to za predpokladu, že väčšia smerodajná odchýlka predstavuje väčšiu preferenciu fuzzy čísla pri maximalizačnom probléme.

Nedostatkom lexikografického prístupu je dominancia prvého kritéria. Napríklad, A a B sú fuzzy čísla a platí $m(B) = m(A)+\epsilon$ , kde $\epsilon$ je malé kladné číslo a $s(B)<<s(A)[/latex], potom fuzzy číslo A je podľa McCahonho kritéria vyhodnotené ako menšie než B. Tento nedostatok môžeme odstrániť agregačným prístupom, ktorým skladáme z viacerých dielčich kritérií celkové kritérium a to na základe sčítania dielčich kritérií s použitím nezáporných váhových koeficientov [latex]w = (w_1,w_2,w_3,\dots)\geq 0[/latex]. Aj keď je agregačný prístup jednokritériálnym porovnávacím indexom, tak nepovažuje rôzne fuzzy čísel za rovnaké. Tento výrok platí za predpokladu vhodne zvolených váhových koeficientov. <p align="justify">Na základe McCahonho kritéria môžeme napríklad navrhnúť kritérium kombinujúce strednú hodnotu a smerodajnú odchýlku ako <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />F^{(3)}(A) = w_1m(A) + w_2s(A)$ , kde $w_1,w_2\geq 0$ .

Príklad 3.1. (Pracovné časy modelované fuzzy číslami)

Modelujme časy spracovania úloh J₁, J₂, J₃ a J₄ pomocou fuzzy trojuholníkových čísel a riešme rozhodovací problém . Existuje niekoľko metód odhadov časov spracovania

min-mean-max
min – modus – max
min – medián – max
aproximácia dát
skúsenost

V tomto príklade použijeme metódu min-modus-max, čo znamená, že ľavá hodnota odhadovaného času spracovania je rovná minimálnej hodnote tréningového súboru z prvého príkladu, stredná hodnota odhadovaného času spracovania je rovná hodnote modus tréningového súboru a pravá hodnota odhadovaného času spracovania je rovná maximálnej hodnote tréningového súboru. Môžeme písať:

$p_1 = (1,8,15),\quad p_2 = (2,9,14),\quad p_3 = (3,3,13)\quad\text{a}\quad p_4 = (2,9,15).$

Najskôr skúsime priradiť úlohu J₄ prvému stroju M₁, (x=1), a získame nasledujúce zaťaženia strojov:

$L_1 = (3,17,30),\quad L_2 = (2,9,14)\quad\text{a}\quad L_3 = (3,3,13)$

Druhou variantou je priradenie úlohy J₄ stroju druhému, (x=2). Ne základe tohoto rozhodnutia vieme spočítať zaťaženia strojov, ktoré sú porade

$L_1 = (1,8,15),\quad L_2 = (4,18,29)\quad\text{a}\quad L_3 = (3,3,13).$

Treťou variantou je, že priradíme úlohu J₄ tretiemu stroju, (x=3), obdržíme tak nasledujúce zaťaženia strojov

$L_1 = (1,8,15),\quad L_2 = (2,9,14)\quad\text{a}\quad L_3 = (5,12,28).$

Teraz nám treba spočítať mieru nerovnomernosti, čo znamená nájsť pre každú variantu minimálne a maximálne zaťaženie. Už v predošlom príklade sme sa stretli s problematikou porovnania intervalov. Porovnanie fuzzy čísel je vo všeobecnosti ešte zložitejšie. V predošlom texte sme spomenuli tri metódy porovnania fuzzy čísel. Mi z nich použijeme agregačnú metódu, pretože má z nich najmenšiu neúspešnosť. Pod pojmom neúspešnosť si môžeme predstaviť počet rôznych fuzzy čísel, ktoré daná metóda považuje za totožné. Váhové koeficienty nastavíme na nasledujúce hodnoty w₁ = 0.5 a w₂ = 0.5. Pre prvú variantu môžeme písať, $F^{(3)}(L_1) = 11.09$ , $F^{(3)}(L_2) = 5.40$ a $F^{(3)}(L_3) = 4.35$ , čo znamená, že maximálne je zaťaženie na prvom stroji a na treťom je minimálne. Miera nerovnomernosti pre prvú variantu je rovná hodnote

$f^{(1)}_{dif}(L_1,L_2,L_3) = L_1 - L_3 = (3,17,30) - (3,3,13) = (-10,14,27)$

Pre druhú variantu vypočítame agregačné indexy, $F^{(3)}(L_1) = 5.43$ , $F^{(3)}(L_2) = 11.06$ a $F^{(3)}(L_3) = 4.35$ . Teda zaťaženie je maximálne na druhom stroji a minimálne na treťom stroji. Miera nerovnomernosti pre druhú variantu nadobúda hodnotu.

$f^{(2)}_{dif}(L_1,L_2,L_3) = L_2 - L_3 = (4,18,29) - (3,3,13) = (-9,15,26)$

Pre tretiu variantu sú agregačné indexy rovné hodnote, $F^{(3)}(L_1) = 5.43$ , $F^{(3)}(L_2) = 5.40$ a $F^{(3)}(L_3) = 9.91$ . Teda podľa agregačného indexu je maximálne zaťaženie na stroji treťom a minimálne na stroji druhom. Miera nerovnomernosti je rovná hodnote

$f^{(3)}_{dif}(L_1,L_2,L_3) = L_3 - L_2 = (5,12,28) - (2,9,14) = (-9,3,26).$

Teraz ešte ostáva porovnať miery nerovnomernosti pre prvú, druhú a tretiu variantu. Podľa agregačného indexu môžeme písať:

$F^{(3)}(f^{(1)}_{dif}) = 8.99,\quad F^{(3)}(f^{(2)}_{dif}) = 8.98\quad\text{ a }\quad F^{(3)}(f^{(3)}_{dif}) = 6.96.$

Tvorca rozvrhu vyberie, vzhľadom na zvolenú metódu odhadu a agregačný index, za optimálny tretí variant.

4. Záver

Cieľom článku bolo oboznámenie čitateľa s nasledujúcimi problematikami rozhodovania pri tvorbe rovnomerných rozvrhov:

problematika modelovania časov spracovania – tu sa tvorca rozvrhu musí rozhodnúť či bude modelovať časy spracovania reálnymi hodnotami, reálnymi intervalmi alebo fuzzy číslami.
problematika predikcie hodnôt z nameraných časov spracovania – akú metódu zvo- líme na predikciu časov spracovania. Pre reálne čísla sú metódy predikcie inakšie ako pre reálne intervaly alebo fuzzy čísla.
problematika porovnania časov spracovania – tu sa tvorca rozvrhu môže stretnúť s problematikou porovnania reálnych intervalov alebo fuzzy čísel.

Z prvého príkladu vieme, že tvorca rozvrhu, používajúci ostré hodnoty (reálne čísla) na modelovanie časov spracovania, dospel k názoru, že optimálny je prvý variant. Z druhého príkladu vieme, že sa tvorca rozvrhu, modelujúci časy spracovania reálnymi intervalmi, rozhodol pre druhý variant. A z posledného príkladu vieme, že sa tvorca rozvrhu rozhodol pre tretí variant. Vidíme, že tri prístupy môžu viesť k trom odlišným výsledkom. Optimálnym rozvrhom je v tomto prípade ten, ktorý najlepšie predikuje hodnoty časov spracovania, podľa ktorých tvorca rozvrhu daný rozvrh navrhne. Ak uvážime, že fuzzy trojuholníkové čísla lepšie popisujú (modelujú) predikované hodnoty ako reálne intervaly alebo reálne hodnoty, môžeme tvrdiť, že by sa tvorca rozvrhu rozhodol pre tretí variant.

Poďakovanie

Táto práca vznikla s podporou grantovej agentúry VEGA vrámci riešenia projektu 1/0374/11 “Modelovanie a optimalizácia mobility a infraštruktúry v logistických sieťach”.

Literatúra

McCahon, C.S., Lee, E.S., Fuzzy job sequencing for a flow shop, European Journal of Opera- tional Research, 1992
Sengupta, A., Pal, T.K., Fuzzy Preference Ordering of Interval Numbers in Decision Problems, Studies in Fuzziness and Soft Computing, Volume 238, ISBN 978-3-540-89914-3, 2009

Žilinská Univerzita, Fakulta riadenia a informatiky, Katedra matematických metód, Univerzitná 8215/1, 010 26 Žilina
²aritmetický priemer obsahuje minoritnú informáciu o početnostiach realizácií časov spracovania

O časopise

Meta

RSS

Problém rozhodovania s neistými dátami

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív