Táto práca sa zaoberá problematikou dynamickej stability synchrónneho generátora, pričom v prvej časti sú opísané základné princípy riešenia a ukazovatele dynamickej stability. Druhá časť pozostáva z dynamických simulácií vybraných udalostí, ktoré sú medzi sebou porovnané z pohľadu významnosti vplývania na dynamickú stabilitu daného generátora.

1. Dynamická stabilita vo všeobecnosti

Počas prevádzky sústavy vzniká mnoho rýchlych zmien, ktoré môžu spôsobiť výraznú nerovnováhu medzi výrobou a spotrebou a teda dochádza k veľkým zmenám záťažných uhlov. Príkladom rýchlych zmien sú napr. spínacie operácie, výpadok veľkého zdroja resp. záťaže, ale najčastejšie sú to skraty, pri vzniku ktorých dochádza ku skokovej zmene väzobnej impedancie sústavy. Na takéto poruchy prirodzene reagujú ostatné generátory zapojené do sústavy. Hoci pri skratoch dochádza ku skokovej zmene väzobnej impedancie, ku skokovej zmene záťažného uhla generátora prísť nemôže kvôli zotrvačnosti sústrojenstva a mechanickým vlastnostiam regulačných obvodov turbíny.

Synchrónne generátory reagujú na rýchle zmeny elektromechanickými kyvmi, prostredníctvom ktorých sa môžu dostať do stavu, kedy sa záťažný uhol ustáli na novej hodnote, alebo bude narastať až po stratu synchronizmu. [1] V reálnej prevádzke by mal každý generátor spĺňať podmienku statickej stability, ale to neznamená, že staticky stabilný generátor musí byť aj dynamicky stabilný. Hlavným rozdielom pri posúdení statickej a dynamickej stability je, že pri statickej stabilite sa určuje, či je prevádzka generátora v ustálenom stave vôbec možná, pričom pri dynamickej sa vyšetruje vplyv a priebeh prechodného deja na synchrónny generátor.

2. Pravidlo rovnosti plôch

Na kvalitatívne posúdenie dynamickej stability synchrónneho generátora sa využíva tzv. pravidlo rovnosti plôch, riešením ktorého sa určí hranica dynamickej stability – kritický uhol δ_krit a z neho kritický čas trvania skratu. Na analýzu dynamickej stability synchrónneho generátora možno využiť zjednodušený model, ktorý je na obr. 1. a jeho náhradná schéma na obr. 2.. Správanie synchrónneho generátora znázorňuje obr. 3., kde je uvedený prechodný dej vypnutia jedného vedenia.

Obr. 1. Zjednodušený model ES [1]

Obr. 2. Náhradná schéma zjednodušeného modelu ES [1]

Obr. 3. Prechodný dej vypnutia jedného vedenia [1]

Na tejto charakteristike sú zobrazené tri krivky. Krivka I predstavuje stav, kedy sú obe vedenia v prevádzke a bod A aktuálne zaťaženie daného generátora, t.j. vyrovnaná výkonová bilancia medzi výrobou a spotrebou. Potom dochádza v dôsledku skratu na vedení V2 ku skokovej zmene väzobnej impedancie (zväčší sa) a tým aj k zmene výkonových pomerov, t.j. krivka II. Keďže sa vplyvom sústrojenstva turbíny nemôže záťažný uhol δ₀ zmeniť skokovo, ostáva na tej istej hodnote, ale dochádza k poklesu odoberaného výkonu – bod A’. Generátor sa tým dostáva do stavu, kedy je odoberaný elektrický výkon menší ako mechanický príkon od turbíny a začne sa urýchľovať, čo spôsobí nárast záťažného uhla – posun z bodu A’ do C.

V bode C dôjde k vypnutiu vedenia, na ktorom vznikol skrat. Zapojeniu s jedným vedením zodpovedá krivka III. Pracovný bod sa presunie z bodu C do C’ na krivke III. Synchrónny stroj bude naďalej urýchľovaný až do bodu D, pretože rotor generátora už získal určitú urýchľujúcu energiu. V tomto bode je odoberaný výkon z generátora väčší ako mechanický príkon od turbíny a generátor začne byť brzdený. Z bodu D sa bude vracať po krivke III. Postupným kývaním sa nakoniec ustáli na rovnovážnej polohe, t.j. bod B pri záťažnom δ₁. [1]

Ako už bolo uvádzané vyššie, na posúdenie dynamickej stability sa používa pravidlo rovnosti plôch, ktoré je možné matematicky odvodiť z pohybovej rovnice synchrónneho generátora:

(1)

kde ω₀ – uhlová rýchlosť, T_m – mechanická časová konštanta, S_n – nominálny výkon predstavujú konštanty. Pohybová rovnica generátora sa upraví rozšírením na oboch stranách o výraz (2dδ/dt) a platí

(2)

kde po úprave derivácie platí

(3)

vykrátením derivácie podľa času dostávame vzťah

(4)

z ktorého pomocou integrovania dostávame

(5)

a pre vyjadrenie časového priebehu uhla δ platí

(6)

Z rovnice (6) je potom možné odvodiť podmienku pre zachovanie dynamickej stability. Generátor je dynamicky stabilný vtedy, keď sa ustáli, t.j. keď sa jeho uhlová rýchlosť ustáli na konštantnej hodnote a teda platí

(7)

z čoho vyplýva z rovnice (6),

(8)

Daný integrál vyjadruje zmenu uhla počas celého trvania prechodného deju, t.j. celé kývanie generátora. Počas tohto kývania je generátor tak urýchľovaný ako i brzdený a interval (δ₀, δ₂) je možné rozdeliť na dva – urýchľujúcu plochu (δ₀, δ₁) a brzdiacu plochu (δ₁, δ₂). Potom je možné rovnicu (8) prepísať do tvaru

(9)

ktorý je vyjadrením pravidla rovnosti plôch, t.j. určuje hranicu dynamickej stability. Z tohto vyplýva, že generátor môže byť dynamicky stabilný iba vtedy, pokiaľ brzdiaca plocha bude väčšia ako urýchľujúca a teda podmienkou dynamickej stability je nerovnosť [1]

(11)

(12)

(13)

Úpravou integrálov dostávame vzťah pre výpočet kritického uhla [1]

(14)

kde

(14)

Na základe vyššie uvedeného platia pre klasifikáciu dynamickej stability synchrónneho generátora základné tri stavy:

1. ak S⁺=S^- – hranica dynamickej stability
2. ak S⁺< S^- – zachovanie dynamickej stability
3. ak S⁺> S^- – strata dynamickej stability

2. Kritický čas trvania skratu (CCT)

Kritický čas trvania skratu je veľmi významný ukazovateľ dynamickej stability a poznať jeho dĺžku sa považuje za praktické posúdenie dynamickej stability synchrónneho generátora. Kritický čas trvania skratu vyjadruje, ako dlho je generátor schopný pracovať do trojfázového skratu na najbližšej prípojnici, kde je vyvedený výkon z tohto generátora a po zániku tejto poruchy udržať sa v synchrónnej prevádzke.

Ak je vypnutie skratu kratšie ako CCT, potom je generátor dynamicky stabilný. Avšak v prípade, že by vypnutie poruchy trvalo dlhšie ako je CCT, mohlo by prísť k strate synchronizmu daného generátora. CCT je možné určiť simulačným experimentom alebo výpočtom vychádzajúc z pohybovej rovnice (1):

(16)

pričom tento vzťah platí iba za predpokladu, že výkon odoberaný z generátora je počas trvania trojfázového skratu rovný nule, t.j. ide o trojfázový skrat na prípojnici vyvedenia výkonu daného generátora. [1] Časové priebehy uhla rotora generátora podľa stavov z obr. 5. sú na obr. 31., kde je znázornené vypnutie 1 – v kritickom čase, 2 – v čase kratšom ako CCT a 3 – čase dlhšom ako CCT.

Pri posudzovaní dynamickej stability sa môže posudzovať tak jeden generátor ako aj celá sústava. Postup pri hodnotení dynamickej stability sústavy pozostáva z určenia kritického času pre všetky synchrónne generátory zapojené do prenosovej sústavy, pričom sa na to využíva konvenčná metóda pravidla rovnosti plôch a verifikácia pomocou dynamických simulácií. Ďalej môžu byť hodnotené dynamické simulácie udalostí N-1, N-k alebo overenie rozpadových miest. Najčastejšie sa výpočty CCT realizujú pri vypracovávaní defence plánov, pri pripájaní nových zdrojov, príprave prevádzky a údržbových stavoch.

Obr. 6. Časové priebehy uhla rotora generátora [1]

3. Faktory ovplyvňujúce dĺžku CCT

Faktory, ktoré môžu ovplyvniť dĺžku trvania CCT sú: [3]

1. skratový výkon v rozvodni, do ktorej je vyvedený výkon daného generátora
2. úroveň napätia v rozvodni, do ktorej je vyvedený výkon daného generátora
3. prevádzkové podmienky generátora, t.j. stav podbudenia resp. prebudenia generátora

Na obr. 7. je zobrazená závislosť kritického času od veľkosti napätia v rozvodni, do ktorej je vyvedený výkon synchrónneho generátora. Z tejto závislosti je zrejmé, že veľkosť trvania CCT výrazne závisí od prevádzkových podmienok generátora a síce, či pracuje v podbudenom alebo prebudenom stave.

Na obr. 8. je závislosť kritického času od veľkosti skratového výkonu v rozvodni, do ktorej je vyvedený výkon synchrónneho generátora, pričom táto charakteristika iba potvrdzuje závislosť trvania CCT od prevádzkového stavu generátora, ale tiež významnosť veľkosti skratového výkonu, najmä pri hodnotách nižších ako S_k”=5GVA, kde je táto závislosť nelineárna. Na základe týchto faktov je potrebné pri určovaní CCT uvažovať s výpočtami pre prebudený stav (Q_gen=max), podbudený stav (Q_gen=min) a pre dodávaný nulový reaktančný výkon (Q_gen=0).

Obr. 7. Vplyv napätia na dĺžku CCT v rozvodni [3]

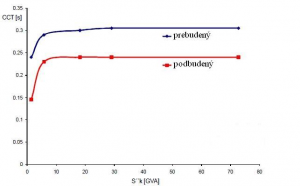
Obr. 8. Vplyv skratového výkonu na dĺžku CCT v rozvodni [3]

4. Dynamické simulácie vybraných udalostí

Simulácie dynamickej stability synchrónneho generátora boli realizované podľa zjednodušeného modelu sústavy, ktorý je na obr. 9.

Obr. 9. Model ES pre hodnotenie dynamickej stability (kde G1-synchrónny generátor; T1-blokový transformátor; TS-tvrdá sieť; AZV-automatika zlyhania vypínača; QM-výkonový vypínač; V1-vedenie)

Cieľom tejto časti bolo namodelovať a porovnať vybrané udalosti (dynamické simulácie udalostí N-1 a N-k), ktoré sa môžu vyskytnúť v reálnej prevádzke ES a uvažuje sa s nimi pri analýzach dynamickej stability ES. Prevádzkové parametre turbogenerátora G1: S_n = 259MVA, U_n=15,8kV, P_G = 221,7MW, Q_G= 29,9MVAr (prebudený stav). Dynamické simulácie boli urobené pre nasledovné vybrané udalosti:

1. prípojnicový skrat v rozvodni s 1,5 vypínačom na odbočku, kde je vyvedený výkon synchrónneho generátora G1
2. 3-f skrat na vedení V1
3. 3-f skrat na vedení V1 so zlyhaním vypínača QM1
4. 3-f skrat na vedení V1 so zlyhaním vypínača QM2
5. 3-f skrat na vedení so zlyhaním vypínačov QM1 a QM2

4.1. Prípojnicový skrat v rozvodni s 1,5 vypínačom na odbočku

Simulácia dynamickej stability bola zameraná na sledovanie správania sa turbogenerátora pri 3-f prípojnicovom skrate v rozvodni s 1,5 vypínačom na odbočku (obr. 10). Takáto rozvodňa sa vyznačuje značnou prevádzkovou bezpečnosťou, čo bude potvrdené simuláciou a používa sa na vyvedenie výkonu z elektrární. Tento typ rozvodne je v podmienkach ES SR využitý pri vyvedení výkonu z JEMO – rozvodňa Veľký Ďur.

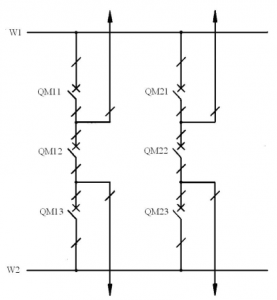
Obr. 10. Rozvodňa s 1,5 vypínačom na odbočku [4]

Simulácia dynamickej stability bola namodelovaná pre stav, kedy dôjde na prípojnici W2 k 3-f skratu, pričom v okamihu skratu sú v prevádzke obe prípojnice. Na túto poruchu zareaguje diferenciálna ochrana prípojnice W2, ktorá posiela vypínacie impulzy na výkonové vypínače QM13 a QM23 a v čase do 100ms po vzniku poruchy sú tieto vypínače vypnuté a rozvodňa ostáva v kontinuálnej prevádzke.

A práve schopnosť ostať v prevádzke po tak závažnej poruche, akou je 3-f skrat na prípojnici vyvedeného výkonu, je silnou stránkou rozvodne s 1,5 vypínačom na odbočku v porovnaní s rozvodňou s jednoduchou prípojnicou. V prípade vzniku 3-f skratu v rozvodni na vyvedenie výkonu s jednoduchou prípojnicou sa musí okamžite synchrónny generátor havarijne vypnúť.

Je potrebné doplniť, že aj napriek zachovaniu kontinuálnej prevádzky generátora, má takáto porucha značný vplyv na jeho dynamickú stabilitu. A práve správanie generátora G1 pri daných prevádzkových parametroch a namodelovanej udalosti (v čase do 10s od vzniku udalosti) je uvedené na obr. 11.

Obr. 11. Správanie SG po prípojnicovom skrate v rozvodni s 1,5 vypínačom na odbočku (kde vt-napätie na svorkách generátora; ang-záťažný uhol, efd-elektromotorické napätie; it-prúd generátora; pg-generovaný výkon; spd-frekvencia)

Z uvedeného priebehu je vidieť, že 3-f prípojnicovom skrate v rozvodni s 1,5 vypínačom došlo k rozkývaniu generátora, ale vzniknutá porucha nepredstavuje stav, ktorý by znamenal havarijné odstavenie generátora. Generátor sa približne do 10s od vzniku poruchy ustálil na novej rovnovážnej polohe a je preto dynamicky stabilný. Hodnoty jednotlivých sledovaných veličín sú uvedené v časti „4.6. Vyhodnotenie vybraných udalostí“.

4.2. 3-f skrat na vedení V1

Ďalší namodelovaný stav bol 3-f skrat na vedení V1. Vedenie je chránené pomocou dištančných ochrán. Dištančná ochrana, v ktorej vypínacej zóne vznikol skrat na vedení V1, na túto poruchu zareagovala a vyslala vypínacie povely na výkonové vypínače na začiatku a na konci vedenia (QM1, QM2), ktoré dané vedenie vypli do 100ms. Správanie synchrónneho generátora G1 je zobrazené na obr. 12., z ktorého je jednoznačné, že po tejto poruche došlo k jeho rozkývaniu, ale napriek tomu ostal v prevádzke a je dynamicky stabilný. K nadobudnutiu novej rovnovážnej polohy došlo približne po 9s.

Obr. 12. Správanie SG po 3-f skrate na vedení V1 (kde vt-napätie na svorkách generátora; ang-záťažný uhol, efd-elektromotorické napätie; it-prúd generátora; pg-generovaný výkon; spd-frekvencia)

Hodnoty jednotlivých sledovaných veličín sú uvedené v časti „4.6. Vyhodnotenie vybraných udalostí“.

4.3. 3-f skrat na vedení V1 so zlyhaním vypínača QM1

Ďalšou modelovanou udalosťou bol 3-f skrat na vedení V1 so zlyhaním vypínača QM1. Vedenie je chránené dištančnými ochranami, pričom vo vypínacej zóne jednej z nich vznikol skrat na vedení V1. Na túto poruchu ochrana zareagovala a vyslala vypínacie povely na výkonové vypínače na začiatku a na konci vedenia (QM1, QM2), pričom vypínač QM2 vypol do 100ms, ale vypínač QM1 zlyhal. V prípade zlyhania výkonového vypínača na vedení, reaguje najbližšia AZV (automatika zlyhania vypínača) k vypínaču, ktorý zlyhal.

AZV je inštalovaná v každej elektrickej stanici (rozvodni) a jej vypínacie časy sú pochopiteľne dlhšie ako je vypínací čas výkonového vypínača, t.j. viac ako 100ms. Pri modelovaní udalostí v tejto práci bol čas vypnutia AZV nastavený na hodnotu 350ms, v ktorom je zahrnutý čas pôsobenia vypínača – 100ms a samotné nastavenie AZV – 250ms. Po poruche vypínača QM1 zareagovala AZV1 v čase 350ms po poruche (obr. 10) a poslala tak vypínacie povely na výkonové vypínače na všetkých vývodoch z prípojnice. Odozva synchrónneho generátora na túto udalosť je znázornená na obr. 13., kde sa opäť turbogenerátor po rozkývaní ustálil približne do 11s od poruchy a je dynamicky stabilný.

Obr. 13. Správanie SG po 3-f skrate na vedení V1 so zlyhaním vypínača QM1 (kde vt-napätie na svorkách generátora; ang-záťažný uhol, efd-elektromotorické napätie; it-prúd generátora; pg-generovaný výkon; spd-frekvencia)

Hodnoty jednotlivých sledovaných veličín sú uvedené v časti „4.6. Vyhodnotenie vybraných udalostí“.

4.4. 3-f skrat na vedení V1 so zlyhaním vypínača QM2

Nasledovný modelovaný stav bol 3-f skrat na vedení V1 so zlyhaním vypínača QM2. Na prvý pohľad sa môže zdať, že ide o podobný stav, ako je predchádzajúci. V skutočnosti ide o podstatne odlišný stav, pretože model sústavy (obr. 10) predstavuje prepojenú sústavu, kde sa zmenou vypínacích časov výrazne mení vplyv na dynamickú stabilitu turbogenerátora G1. Simulácia nakoniec túto skutočnosť potvrdí.

Rovnako ako pri predchádzajúcom stave je vedenie V1 chránené dištančnými ochranami. Vo vypínacej zóne dištančnej ochrany vznikne skrat na vedení V1, na čo ochrana zareaguje, posiela vypínacie povely na výkonové vypínače na začiatku a na konci vedenia (QM1, QM2), pričom teraz vypínač QM1 vypne v čase 100ms, ale vypínač QM2 zlyhá. Na zlyhania vypínača QM2 reaguje AZV2 (automatika zlyhania vypínača) a vypína všetky vývody na prípojnici v čase 350ms. Synchrónny generátor (obr. 14) sa opäť rozkýva a do 9s po tejto udalosti sa ustáli na novej rovnovážnej polohe, t.j. je dynamicky stabilný.

Obr. 14. Správanie SG po 3-f skrate na vedení V1 so zlyhaním vypínača QM2 (kde vt-napätie na svorkách generátora; ang-záťažný uhol, efd-elektromotorické napätie; it-prúd generátora; pg-generovaný výkon; spd-frekvencia)

Hodnoty jednotlivých sledovaných veličín sú uvedené v časti „4.6. Vyhodnotenie vybraných udalostí“.

4.5. 3-f skrat na vedení V1 so zlyhaním vypínačov QM1 a QM2

Medzi udalosti (aj keď veľmi málo pravdepodobné), pre ktoré sa overujú dynamickými simuláciami, patrí aj zlyhanie vypínačov na oboch koncoch vedenia. V tomto prípade bola situácia modelovaná spôsobom, že na vedení V1 došlo k 3-f skratu, na čo zareagovala dištančná ochrana, ktorá vyslala vypínacie povely na výkonové vypínače, no tieto zlyhali. Z tohto dôvodu došlo k zareagovaniu AZV na oboch prípojniciach (AZV1, AZV2), kde je V1 pripojené (obr. 10). AZV na oboch prípojniciach zareagovalo v čase do 350ms a boli vypnuté všetky vývody z daných prípojníc. Synchrónny generátor sa po tejto udalosti prirodzene rozkýval a k nadobudnutiu nového rovnovážneho stavu došlo približne po 11s, čo znamená, že ani táto udalosť neznamenala ohrozenie dynamickej stability daného generátora.

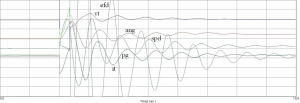
Obr. 15. Správanie SG po 3-f skrate na vedení V1 so zlyhaním vypínačov QM1 a QM2 (kde vt-napätie na svorkách generátora; ang-záťažný uhol, efd-elektromotorické napätie; it-prúd generátora; pg-generovaný výkon; spd-frekvencia)

4.6. Vyhodnotenie vybraných udalostí

Zobrazené priebehy zrealizovaných dynamických simulácií sú vhodným grafickým zobrazením odozvy turbogenerátora na vybrané modelované udalosti, ale až v tab. 1. sú vyčíslené efektívne hodnoty sledovaných veličín, z ktorých je možné vyvodiť relevantné závery. Modelované udalosti možno zoradiť z pohľadu ich vplývania na dynamickú stabilitu synchrónneho generátora od najviac vplývajúcej nasledovne:

1. 3-f skrat na V1 so zlyhaním QM1 a QM2
2. 3-f skrat na V1 so zlyhaním QM1
3. 3-f skrat na V1 so zlyhaním QM2
4. 3-f skrat na V1

pričom rozhodujúcim kritériom je veľkosť kolísania záťažného uhla, frekvencie, generovaného výkonu a prúdu. Samostatným príkladom udalosti je prípojnicový skrat, ktorý by som nechcel priamo porovnávať s ostatnými udalosťami, pretože v tomto prípade ide o špeciálne zapojenú rozvodňu a ide o elektricky veľmi blízky skrat, ktorý má vždy výraznejší vplyv na dynamickú stabilitu ako skraty na iných miestach ES. Z výsledkov možno konštatovať, že skraty vypínané v rýchlom čase (100ms) neohrozujú dynamickú stabilitu tak ako poruchy vypínané v dlhšom čase (AZV).

Tab. 1. Hodnoty sledovaných veličín pri simuláciách dynamickej stability synchrónneho generátora

udalosť		prípojnicový skrat	3-f skrat na V1	3-f skrat na V1 so zlyhaním QM1	3-f skrat na V1 so zlyhaním QM2	3-f skrat na V1 so zlyhaním QM1 a QM2
napätie na svorkách generátora [kV]	min	5,46	11,42	10,16	11,42	10,68
	max	16,46	16,12	16,76	16,48	16,77
záťažný uhol [°]	min	2,8962	12,013	3,4877	7,901	1,3962
	max	44,071	29,699	51,339	28,812	56,226
prúd [A]	min	4521,98	6840,69	3829,2	6245,4	3205,51
	max	27982,68	12928,99	18413,47	12928,99	17520,05
generovaný výkon [MW]	min	6,4605	120,15	107,88	120,15	89,834
	max	371,67	286,7	392,62	296,26	401,83
frekvencia [Hz]	min	49,7	49,875	49,64	49,84	49,61
	max	50,425	50,18	50,255	50,18	50,315

6. Odkazy na literatúru

1. REVÁKOVÁ, D. – ELESCHOVÁ, Ž. – BELÁŇ, A. Prechodné javy v elektrizačných sústavách. Bratislava : Vydavateľstvo STU, 2008. 180 s. ISBN 978-80-227-2868-3
2. ELESCHOVÁ, Ž. – BELÁŇ, A. CCT – basic criteria of power system transient stability. In Electric Power Engineering. Brno : Vysoké učení technické v Brňe, 2010. APVV-0337-07, p. 157-161.
3. ELESCHOVÁ, Ž. – BELÁŇ, A. Factors affecting the length of critical clearing time. In 9th International Conference : Control of Power Systems. Tatranské Matliare High Tatras : FEI STU, 2010. APVV-0337-07, p. 1-7.
4. JANÍČEK, F. – ARNOLD, A. – GORTA, Z. Elektrické stanice. Bratislava : Vydavateľstvo STU, 2001. 286 s. ISBN 80-227-1630-8

---

Spoluautorom článku je doc. Ing. Žaneta Eleschová, PhD., Katedra elektroenergetiky, Fakulta elektrotechniky a informatiky STU

---

Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Elektroenergetika a získala Cenu Dekana, ISBN 978-80-227-3508-7