Erlangove rovnice a ich využitie v asynchrónnych sieťach
24. Október, 2011, Autor článku: Weber Adam, Informačné technológie, Študentské práce
Ročník 4, číslo 10  Pridať príspevok
Pridať príspevok
![]() Článok sa zaoberá využitím Erlangových rovníc v asynchrónnych sieťach. Analyzuje možnosti využitia Erlangových rovníc B a C v asynchrónnych sieťach a špecializuje sa na parametre pravdepodobnosti stratovosti a oneskorenia. Je navrhnutý simulačný model sieťovej topológie, pomocou ktorého sú simulované metódy využívané na hodnotenie prevádzky v asynchrónnych sieťach. Hlavným bodom tohto článku je zhodnotenie výsledkov jednotlivých metód v porovnaní s výsledkami Erlangových rovníc. Taktiež sú opísané všeobecné poznatky, a ako je možné využiť Erlangove rovnice v asynchrónnych sieťach.
Článok sa zaoberá využitím Erlangových rovníc v asynchrónnych sieťach. Analyzuje možnosti využitia Erlangových rovníc B a C v asynchrónnych sieťach a špecializuje sa na parametre pravdepodobnosti stratovosti a oneskorenia. Je navrhnutý simulačný model sieťovej topológie, pomocou ktorého sú simulované metódy využívané na hodnotenie prevádzky v asynchrónnych sieťach. Hlavným bodom tohto článku je zhodnotenie výsledkov jednotlivých metód v porovnaní s výsledkami Erlangových rovníc. Taktiež sú opísané všeobecné poznatky, a ako je možné využiť Erlangove rovnice v asynchrónnych sieťach.
1. Úvod
Erlangove rovnice sú pravdepodobnostným nástrojom QoS parametrov a to oneskorenia, stratovosti a šírky prenosového pásma. V súčasnosti sa kladie veľký dôraz na tieto koeficienty z pohľadu zabezpečenia prevádzky jednotlivým užívateľom. Je mnoho mechanizmov a metód, ktoré sa zaoberajú ich vyriešením a správnym popisom. Z pohľadu vývoja a skúmania jednotlivých spôsobov charakterizovania prevádzky sú jednotlivé metódy a techniky hodnotenia prevádzky rozdelené do dvoch kategórii: meracie techniky a prediktívne metódy. Častokrát tieto prediktívne mechanizmy sú náročné na realizáciu a zdĺhavé kvôli matematickej analýze a výpočtovej náročnosti. Erlangove rovnice patria taktiež do kategórie prediktívnych metód.
2. Erlangove rovnice
Erlangove rovnice sú určené na analýzu prevádzky v synchrónnych sieťach, kde prevádzka je spojovo orientovaná. Pre analýzu a uplatnenie Erlangových rovníc v asynchrónnej prevádzke je nutné upraviť parametre tak, aby mali spoločné znaky synchrónnych a aj asynchrónnych sietí:
- B [%] – pravdepodobnosť stratovosti,
- C [%] – pravdepodobnosť oneskorenia,
- A [%] – využitie linky,
- N [Mbit/s] – šírka prenosového pásma.
2.1. Simulačný model
Topológia siete na Obr. 1. je zostavená zo šiestich sieťových uzlov, pričom vstupné linky majú šírku prenosového pásma 10 Mbit/s. Všetky tieto vstupné linky smerujú do jedného sieťového uzla, ktorého výstupná linka ma šírku prenosového pásma 15 Mbit/s. Meranie pre jednotlivé metódy a Erlangove rovnice sa bude uskutočňovať na výstupnom uzle.
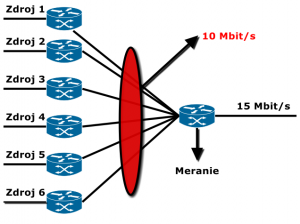
Obr. 1. Topológia simulačného modelu.
Tok dátových vzoriek na Obr. 2. predstavuje zachytené vzorky, ktoré reprezentujú každý jeden zdroj. Tieto dátové vzorky sú zachytené vo výstupnom uzle a v ňom sa bude vykonávať meranie, či už pre Erlangove rovnice alebo pre jednotlivé metódy. Tieto merania budú mať za úlohu skúmanie pravdepodobnosti oneskorenia a stratovosti. Vygenerovanie prevádzky a teda priebeh celkovej simulácie trvá 33 minút a 20 sekúnd. Počas prevádzky boli zaznamenané základne hodnoty rýchlosti toku dát:
- PCR = 13,424 Mbit/s
- SCR = 8,198 Mbit/s
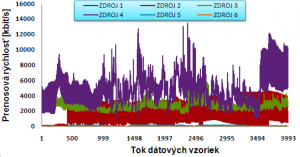
Obr. 2. Prevádza na výstupnom uzle.
3. Výsledky z pohľadu pravdepodobnosti stratovosti
Jednotlivé výsledky metód sú realizované v sieťovej topológii na výstupnom uzle. Výstupný uzol zachytáva celkovú prevádzku, ktorá je prostriedkom pre výpočet pravdepodobnosti stratovosti a oneskorenia. Každý dátový tok reprezentuje jeden zdroj prevádzky.
3.1. Erlangova rovnica B
Prvá Erlangova rovnica umožňuje stanoviť pravdepodobnosť vzniku stratovosti volania B pri zadanom počte N využitých liniek a pri určenej celkovej ponúknutej prevádzke A [1, 2, 3].
| (1) |
kde: B – podiel stratených volaní, A – celková ponúknutá prevádzka [Erl], N – počet kanálov (liniek).
Výsledok Erlangovej rovnice, ktorá vyrátava pravdepodobnosť stratovosti, zobrazuje Obr. 3.
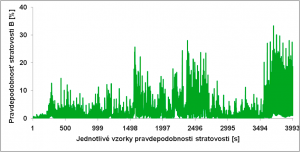
Obr. 3. Výsledok prav. stratovosti prostredníctvom Erlangovej rovnice B.
Charakterizovanie prevádzky z pohľadu prav. stratovosti je nasledovné:
- pravdepodobnosť stratovosti dosahuje maximálne hodnoty v čase 29 minút a 48 sekúnd,
- maximálne hodnoty pravdepodobnosti stratovosti dosahujú 33.28 %,
- minimálne hodnoty pravdepodobnosti kolíšu okolo hodnoty 0.0001026 %,
- počas celej simulácie a teda časovej doby 33 minút 20 sekúnd bola priemerná pravdepodobnosť stratovosti 2.511%.
3.2. Metóda “BCTQM – Basic continuous- time queuing model“
Vychádza sa z predpokladu, že príchodzie požiadavky (dátové vzorky) majú exponenciálne rozdelenie. Model systému je znázornený na Obr. 4.
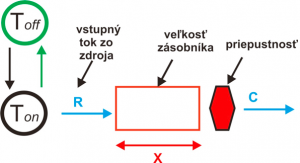
Obr. 4. Model zdroja pre metódu kontinuálneho toku (BCTQM).
Analýza tohto modelu si vyžaduje čiastočné použitie diferenciálnych rovníc a ich odvodenie je príliš zložité. Avšak, ich odvodením vznikla rovnica (2) pre priemernú pravdepodobnosť stratovosti, ktorá je nasledovná [1]:
| (2) |
kde: R – vstupný dátový tok zo zdroja, keď je v stave ON [kbit/s], C – výstupný dátový tok, ktorý vychádza zo zásobníka [kbit/s], X – veľkosť zásobníka v čakacom rade [kbit/s], Ton – priemerná doba v stave ON [s], Toff – priemerná doba v stave Off [s].
3.3. Metóda “BDTQM – Basic discrete-time queuing model”
Metóda čakacieho radu diskrétneho-časového modelu je uplatnená prostredníctvom systému hromadnej obsluhy ON-OFF/D/1/k. Metóda je vhodná pre jednotlivé toky prevádzky, alebo pre scenár jednotlivých virtuálnych ciest. Vzorce sú nasledujúce:
| (3) |
| (4) |
| (5) |
| (6) |
kde: R – vstupný dátový tok zo zdroja, keď je v stave ON [kbit/s], C – výstupný dátový tok, ktorý vychádza zo zásobníka [kbit/s], X – veľkosť zásobníka v čakacom rade [kbit/s], Ton – priemerná doba v stave ON [s], Toff – priemerná doba v stave Off [s], p(k) – pravdepodobnosť vstupného toku odhadnutá v zásobníku [%], CLP – pravdepodobnosť stratovosti bunky / paketu [%].
Táto metóda analyzuje každú príchodziu dátovú vzorku Obr. 5. Namiesto hľadania pravdepodobnostného stavu na konci zadanej časovej periódy sa odhaduje pravdepodobnosť príchodzej dátovej vzorky v zásobníku. Ak vstupný dátový tok vzoriek zistí, že zásobník je plný, tak tento tok je zahodený a preto CLPvst.-toku je jednoducho vyjadrenie pravdepodobnosti s akou táto situácia môže nastať[1].
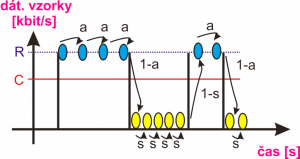
Obr. 5. Analyzovanie príchodzej dátovej vzorky.
3.4. Metóda “BSQM – Burst-scale queuing model”
Táto metóda je uplatnená prostredníctvom využitia burst-scale (tzn. na základe určitého príchodzieho množstva buniek alebo paketov, teda zhlukov) modelu čakacieho radu pre IP a ATM siete. Kombinuje stratovú burst-scale analýzu, ktorú je možné uplatniť aj pre oneskorenú prevádzku. Metóda využíva viacnásobný počet ON/OFF zdrojov, ktoré vytvárajú prevádzku pre ATM, alebo IP zásobník. Táto situácia viacnásobného počtu zdrojov je zobrazená na Obr. 6. [1, 2]. Vzorce pre BSQM metódu sú nasledujúce:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
kde: N – celkový počet ON/OFF zdrojov, Ton – priemerná doba v stave ON – pre jeden zdroj [s], Toff – priemerná doba v stave Off – pre jeden zdroj [s], h – vstupný dátový tok pre jeden zdroj [kbit/s], m – priem. vst. tok dát. vzoriek pre zdroj [kbit/s], C – maximálna kapacita zásobníka [kbit], λ – počet zhlukov príchodzích za jednotku času [s], b – priemerný počet buniek / paketov v jednom zhluku, ρ – ponúkaná prevádzka, ktorá je obsluhovaná [%], N0 – minimálny počet aktívnych zdrojov pre BSQM, CLPvst.-toku – pravdepodobnosť stratovosti [%].
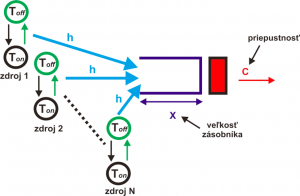
Obr. 6. Model viacnásobného počtu ON/OFF zdrojov.
Aproximačná analýza tohto burst-scale modelu je založená na type M/N/N systému hromadnej obsluhy (kde N je celkový počet zdrojov a N0 je minimálny počet aktívnych zdrojov), ktorý umožňuje vypočítať celkovú prav. stratovosti podľa rovnice (12).
4. Výsledky z pohľadu pravdepodobnosti oneskorenia
Jednotlivé výsledky metód pre pravdepodobnosť oneskorenia sú realizované podobne ako boli realizované výsledky pre pravdepodobnosť stratovosti (kap. 3). Sú realizované v sieťovej topológii (Obr. 1.) na výstupnom uzle, ktorý bude mať obmedzenú kapacitu prenosového pásma na 15 Mbit/s.
4.1. Erlangova rovnica C
Druhá Erlangova rovnica určuje pravdepodobnosť doby čakania klienta na službu pri vzniku čakacieho radu, pričom blokované hovory ostanú v obsluhovom systéme až do doby, pokiaľ nebudú požiadavky obslúžené.
| (13) |
, pričom N>A. Druhú Erlangovu rovnicu C (13) je možné zjednodušiť do tvaru:
| (14) |
Výsledok Erlangovej rovnice pre prav. oneskorenia zobrazuje Obr. 7. Z pohľadu pravdepodobnosti oneskorenia je možne určiť nasledovné [2, 3, 5]:
- maximálne hodnoty pravdepodobnosti oneskorenia dosahujú 100%,
- keby nebola určujúca podmienka (N<A), hodnoty pravdepodobnosti oneskorenia by boli väčšie než 100%,
- minimálne hodnoty pravdepodobnosti oneskorenia sú zanedbateľné, pohybujú sa okolo 0.0013%.
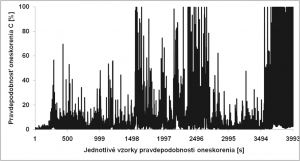
Obr. 7. Výpočet pravdep. oneskorenia prostredníctvom Erlangovej rovnice C.
4.2. Metóda “CCTQM – Classical continuous-queuing model”
Metóda CCTQM je uplatnená pre model systému M/M/1, ktorý umožňuje určiť pravdepodobnosť oneskorenia, ktoré môže nastať pri prevádzke. Na základe nasledujúcich vzťahov je možné určiť pravdepodobnosť oneskorenia:
| (15) |
| (16) |
| (17) |
| (18) |
kde: ρ – využitie, záťaž ponúkaná systému [%], q – priemerný počet čakajúcich alebo momentálne obslúžených požiadaviek v systéme, tw – priemerný čas vzniknutý čakaním za obsluhou [s], X – veľkosť kapacity zásobníka [kbit/s], s – priemerná obslužná doba pre každého zákazníka [s].
Uplatnením rovnice (16) je možné vyrátať oneskorenie, ktoré nastalo čakaním za obsluhou [1, 5].
4.3. Metóda uplatnená pri maximálnom využití systému “MS“
Táto metóda je uplatnená a odvodená z Erlangovej rovnice C. Predpokladá sa, že pakety alebo bunky sú zaraďované do čakacieho radu, pretože prenosové pásmo je obmedzené. Táto metóda určuje pravdepodobnosť, že pakety budú oneskorené viac než t sekúnd pri maximálnom využití systému.
| (19) |
kde: t – paket je oneskorený o t sek [s], H – čas trvania paketu [s].
Táto metóda je nenáročná na výpočet, pretože so základnými parametrami (A, H) sa dá veľmi ľahko určiť pravdepodobnosť oneskorenia [4].
4.4. Littleho rovnica
Priemerný počet dátových vzoriek v zásobníku úzko súvisí s priemerným časom akým ich systém, teda zásobník, obsluhuje. Čas jednotlivých dátových vzoriek strávených čakaním v zásobníku určuje Littleho rovnica [1, 3, 6].
Tab. 1. Tvary Littleho rovnice.
| Littleho rovnica | ||
|---|---|---|
| Základná | Jeden server | Mnohonásobný server |
kde: q – priemerný počet paketov / buniek v systéme, ρ – linkové využitie (je to podiel prevádzky, ktorá je momentálne obsluhovaná) [%], µ – vstupný prevádzkový tok [kbit/s], W – priemerný počet paketov / buniek, ktoré čakajú na obsluhu, λ – miera príchodu.
5. Porovnanie výsledkov a analýza jednotlivých metód
Tieto výsledky jednotlivých metód môžu zodpovedať a riešiť problémy, ktoré sa vyskytujú v asynchrónnych sieťach. Korektné výsledky sú dosiahnuté len vtedy, ak metódy sú uplatnené pre správny systém a správnu sieťovú topológiu. Keďže ide o prediktívne metódy, dosiahnutie takýchto výsledkov si vyžaduje širokú znalosť systémov hromadnej obsluhy a správne aproximovanie takéhoto systému na sieťovú topológiu. Jednotlivé výsledky v kapitole 5.1 sú toho dôkazom.
5.1. Zhodnotenie a porovnanie jednotlivých metód
Pre všetky metódy v sieťovej topológii je rovnaká prevádzka, ktorá má hodnotu priemerného využitia linky 54.65%. Hlavným dôvodom použitia rovnakej prevádzky u všetkých metód je možnosť ich vzájomného porovnania. Keby nebola uplatnená rovnaká koncepcia, tak by to nebolo možné. Výsledky jednotlivých metód z pohľadu pravdepodobnosti stratovosti sú uvedené v Tab. 2 a Obr. 8.
Tab. 2. Porovnanie metód pravdep. stratovosti.
| Priemerná prav. stratovosti [%] | Množstvo stratených paketov [kbit] | Priemerné využitie linky [%] | |
|---|---|---|---|
| Erlang B | 2.51 | 252.11 | 54.65 |
| BCTQM | 2.38 | 228.06 | |
| BDTQM | 3.28 | 585.85 | |
| BSQM | 2.58 | 266.46 |
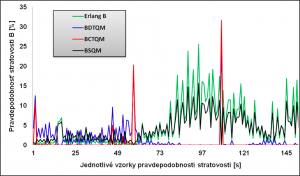
Obr. 8. Výber pravdepodobnostných vzoriek stratovosti pre jednotlivé metódy.
Porovnanie z pohľadu pravdepodobnosti stratovosti:
- najlepšie výsledky dáva metóda BCTQM. Priemerná pravdepodobnosť stratovosti paketov je najnižšia a má hodnotu 2.38%. Množstvo stratených paketov počas 34 minútovej simulácie bol 228, 06 kbit,
- najhoršie výsledky sú získane využitím metódy BDTQM. Priemerná pravdepodobnosť stratovosti bola najvyššia a to 3.28%. Celkové množstvo stratených paketov bol 585.85 kbit,
- Erlangova rovnica B vypočítala adekvátne hodnoty pravdepodobnosti oneskorenia. Je možné teda konštatovať, že správnym uplatnením tejto rovnice je možné dosiahnuť výsledky, ktoré sú veľmi podobné výsledkom metód využívaných v asynchrónnej sieti.
Z pohľadu pravdepodobnosti oneskorenia sú výsledky jednotlivých metód zobrazené v Tab. 3 a na Obr. 9.
Tab. 3. Porovnanie metód pravdep. oneskorenia.
| Priemerná prav. oneskorenia [%] | Množstvo oneskor. paketov [kbit] | Priem. využ. linky [%]/th> | |
|---|---|---|---|
| Erlang C | 8.79 | 3 094.91 | 54.65 |
| CCTQM | 9.99 | 3 994.39 | |
| MS | 8.49 | 2 886.71 | |
| Littleho r. | 1.86 | 139,09 |
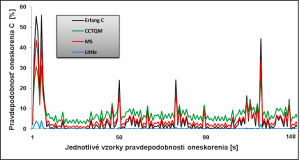
Obr. 9. Výber pravdepodobnostných vzoriek oneskorenia pre jednotlivé metódy.
Porovnanie z pohľadu pravdepodobnosti oneskorenia:
- najlepšie výsledky dosiahla metóda s využitím Littleho rovnice. Priemerná pravdepodobnosť stratovosti paketov je najnižšia a má hodnotu 1.86%. Množstvo oneskorených paketov počas 34 minútovej simulácie bol 139.09 kbit. Výsledky, ktoré boli získané prostredníctvom Littleho rovnice sa značne líšia od ostatných metód. Hlavným dôvodom tohto rozdielu je funkcionalita uplatnenia Littleho rovnice, pretože túto rovnicu je možné uplatniť len pre dátové toky a služby, ktoré využívajú minimálnu šírku prenosového pásma z celkovej ponúkanej prenosovej kapacity linky.
- najhoršie výsledky sú získane využitím metódy CCTQ, ktorá využíva základný systém hromadnej obsluhy. Priemerná pravdepodobnosť stratovosti bola najvyššia a to 9.99%. Celkové množstvo stratených paketov presiahol hodnotu 3994,39 kbit,
- pri Erlangovej rovnici C boli zistené hodnoty: priemerná pravdepodobnosť oneskorenia 8.79% a celkové množstvo oneskorených paketov bolo 3094.91 kbit.
Základné zistenia pre prvú a druhú Erlangovu rovnicu v asynchrónnych sieťach sú:
- ak dátový tok v uzle presiahne maximálnu kapacitu prenosového pásma, dochádza k strate informácie,
- ak uzol v sieťovej topológii obsahuje vyrovnávaciu pamäť, potom po presiahnutí maximálnej kapacity šírky prenosového pásma v uzle dôjde k oneskoreniu paketov,
- pri situácii prekročenia vyrovnávacej pamäte nastavajú stratovosti (tzn. dochádza k 100% pravdepodobnosti stratovosti paketov),
- pri výpočte Erlangovej rovnice nemôže byť parameter A väčší ako N.
Z pohľadu Erlangovej rovnice C je parameter pravdepodobnosti oneskorenia C, závislý od parametra pravdepodobnosti stratovosti B, ktorú vypočítava Erlangova rovnica B. Závislosť je spôsobená z dôvodu využitia parametra pravdepodobnosti stratovosti B v druhej Erlangovej rovnici C (14).
5.2. Všeobecné využitie Erlangových rovníc pre asynchrónne siete
Problém:
V dnešných asynchrónnych sieťach je preťaženie jedným z najväčších problémov a môže byť spôsobený viacerými faktormi:
- zlé dimenzovanie siete,
- veľký počet užívateľov,
- staršie verzie protokolov, ktoré využívajú veľkú šírku prenosového pásma,
- a iné.
Riešenie a využitie:
- Erlangove rovnice by mohli zabrániť zlému dimenzovaniu siete. Pred výstavbou sieťovej topológie by sa v simulačnom programe vopred nakonfigurovala požadovaná sieťová topológia a na jednotlivé uzly v sieti by sa implementovali Erlangove rovnice. Rovnice by poskytovali výsledky pravdepodobnosti oneskorenia a stratovosti. Keby sa prekročili prahové hodnoty týchto parametrov, znamenalo by to nevhodné dimenzovanie siete a dochádzalo by v tejto sieti k neprijateľným stratám paketov a taktiež k oneskoreniu.
- Na základe štatistických údajov, by bolo možné uplatniť Erlangove rovnice aj ďalším spôsobom: rovnice môžu odhadovať aktuálny počet užívateľov v sieti a mohli by napomôcť zistiť, ktorí užívatelia najviac zaťažujú prevádzku.
- Erlangove rovnice by mohli hybridne pracovať s metódami riadenia prístupu, teda AC metódami. Využitie by spočívalo v zistení, či má alebo nemá byť sprístupnená služba pre konkrétneho užívateľa.
- Účelom Erlangových rovníc by mohlo byť aj uplatnenie v programe, ktorý analyzuje sieťovú prevádzku. Program by poskytoval výsledky kvality zabezpečenia služby z pohľadu parametrov oneskorenia a stratovosti.
6. Záver
Úlohou tohto článku bola realizácia Erlangovej rovnice B a Erlangovej rovnice C pre navrhnutý simulačný model sieťovej topológie. Tento model bol hlavným prvkom, ktorý umožnil overenie využitia Erlangovej rovnice B a Erlangovej rovnice C v asynchrónnych sieťach na základe porovnania výsledkov, ktoré poskytli ďalšie uplatnené metódy. Tieto metódy boli taktiež realizované na tej istej sieťovej topológii.
Z pohľadu pravdepodobnosti stratovosti, ktorou sa zaoberá Erlangova rovnica B to boli nasledujúce metódy: BDTQM, BCTQM, BSQM a metódy zaoberajúce sa Erlangovu rovnicou C, teda parametrom pravdepodobnosti oneskorenia, to boli nasledujúce metódy: CCTQM, MS a Littleho rovnica.
Overenie uplatnenia Erlangových rovníc bolo realizované v podobe porovnania výsledkov, ktoré poskytovali jednotlivé metódy a Erlangove rovnice. Výsledky sú spísané v kapitole 5, a tá sa delí na dve častí:
Časť 1: Boli vyhodnotené a porovnané výsledky jednotlivých metód. Taktiež sa určili všeobecné poznatky Erlangových rovníc v asynchrónnych sieťach.
Časť 2: Na základe naštudovaných informácii a ich uvedení v tomto článku prostredníctvom jednotlivých kapitol bol zrealizovaný návrh, ako je možné využívať Erlangove rovnice v asynchrónnych sieťach.
10. Odkazy na literatúru
- Pitts, J.M., Schormans, J.A.: Introduction to IP and ATM Design Performance (Second Edition), John Wiley & Sons, Ltd, University of London, UK, 12 Oct. 2001, Print ISBN: 9780471491873, Online ISBN: 9780470841662
- Cooper, R.B.: Introduction to Queueing Theory: 2nd Edition, Elsevier, 1980, ISBN 0444010653, 9780444010650
- Kobayashi, H., Mark, L.B.: Generalized Loss Models and Queueing-loss Networks, Intl. Trans. In Op. Res. 9, 2002, str. 97 – 112
- Vennuci, D.J., Chitamu, P.J.: Efficient Radio Resource Allocation in a GSM and GPRS Cellular Network, Systemics, Cybernetics and Informatics vol. 2 num. 5.,University of Witwatersrand, Johannesburg 2004
- Hayes, J. F., Ganesh, B.: Modeling and Analysis of Telecommunications Networks, Wiley-IEEE, 2004, ISBN 0471348457, 9780471348450
- Hardy, W.: QoS: Measurement and Evaluation of Telecommunications Quality of Service, John Wiley and Sons, 2001, ISBN 0471499579, 9780471499572
Spoluautor článku je Ing. Erik Chromý, PhD., Katedra telekomunikácií, Fakulta elektrotechniky a informatiky, Slovenská technická univerzita, Ilkovičova 3, 812 19 Bratislava
Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Telekomunikácie VI. a získala Cenu IEEE, ISBN 978-80-227-3508-7

