Kontaktné centrum je systém hromadnej obsluhy, jeho úlohou je uspokojiť požiadavky zákazníkov. Kontaktné centrum vytvára profesionálny imidž spoločnosti, preto musí byť vhodne navrhnuté. Článok sa zaoberá modelovaním jednoduchého kontaktného centra pomocou markovovského modelu M/M/m/K. Model kontaktného centra je podrobený analýze pre rôzne situácie. Ďalej je rozoberaná optimalizácia kontaktného centra z pohľadu počtu agentov.

1. Úvod

Kontaktné centrum je dôležitým komunikačným nástrojom pre spoločnosť, ktorá chce byť v kontakte so svojimi zákazníkmi. Pri zriaďovaní kontaktného centra je treba dbať na efektivitu vynaložených prostriedkov. Spoločnosť sa snaží obslúžiť čo najväčší počet zákazníkov. Kontaktné centrum musí byť optimalizované z pohľadu veľkosti kontaktného centra, personálnych a technických prostriedkov. Všetky tieto prostriedky sa odvíjajú od počtu zákazníkov, ktorí kontaktujú centrum.

Vstupný tok zákazníkov je náhodný, čiže v rôznych časových intervaloch prichádzajú rôzne počty zákazníkov (napr. v jednom časovom intervale môže prísť hneď niekoľko zákazníkov, a zase v inom okamihu nemusí prísť žiaden). Takisto aj čas obsluhy zákazníka je náhodný. Keď je veľký počet požiadaviek a kontaktné centrum nestíha ihneď vybavovať požiadavky zákazníkov, zákazníci musia počkať na obsluhu v čakacom rade. Čakací rad má len určitú veľkosť. Keď sa naplní aj čakací rad a ďalší zákazníci požadujú obsluhu, ich volania budú stratené. Počet stratených volaní musí byť čo najmenší. Pri malom počte vstupujúcich zákazníkov (t.j. počet volaní je menší ako počet agentov), agenti ktorí nevykonávajú obsluhu majú prestoje a systém je neefektívny. Preto je potrebné stanoviť správny počet agentov (počet agentov v rôznych dňoch a hodinách môže byt odlišný).

V praxi nie je možné určiť presný čas príchodu volania, ale je možné určiť pravdepodobnosť, v akom okamihu príde ďalší hovor. Poissonovo rozdelenie vyjadruje pravdepodobnosť výskytu určitého počtu javov za určitý čas. Čiže vstupný tok zákazníkov sa riadi Poissonovým rozdelením [1].

Markovovské systémy hromadnej obsluhy sú také systémy, ktoré je možné modelovať pomocou markovovského reťazca so spojitým časom. Pre takýto systém platí markovova vlastnosť, ktorá vyjadruje, že budúcnosť závisí len od prítomnosti, nie od minulých stavov, tzv. “zabúdanie na minulosť“. Z markovovských modelov je najvhodnejší model M/M/m/K, pretože agentov je len určitý počet a dĺžka čakacieho radu je obmedzená. V prevádzke nemá zmysel uvažovať o modeloch, ktoré majú nekonečný čakací rad.

2. Modelovanie prevádzky markovovským modelom M/M/m/K

Agenti kontaktného centra obsluhujú požiadavky, ktoré prichádzajú v náhodných časových okamihoch, čiže príchod zákazníkov je náhodná premenná s Poissonovým rozdelením. Čas obsluhy zákazníka má exponenciálne rozdelenie. Hlavné parametre kontaktného centra sú:

• kapacita systému, t.j. počet požiadaviek, ktoré je systém schopný obslúžiť – parameter μ,
• počet agentov – parameter m,
• dĺžka čakacieho radu K
• požiadavky vstupujú do systému intenzitou .

Predpokladajme, že kontaktné centrum za jednu hodinu dokáže v priemere obslúžiť 1200 zákazníkov a má desať agentov. Je možné modelovať dve situácie:

• ak je zaťaženie systému ρ < 1,
• ak je zaťaženie systému ρ > 1 (t.j. systém je preťažený).

a) zaťaženie systému ρ < 1

Ak zaťaženie systému ρ je menej ako 1, potom intenzita vstupujúcich požiadaviek je menšia ako počet požiadaviek, ktoré je systém schopný obslúžiť (čiže < μ). Nech je počet vstupných požiadaviek = 1000 za hodinu a μ = 1200 požiadaviek za hodinu. A nech počet agentov je 10. Modelujeme situáciu pomocou systému M/M/m/K. Pre zjednodušenie výpočtu dĺžka čakacieho radu K je zhodná s počtom agentov m.

Parametre systému sú: = 1000, μ = 1200, m=10

Výpočet zaťaženia systému:

(1)

Z uvedeného vyplýva, že zaťaženie systému ρ < 1, čiže systém nie je preťažený. Potom pravdepodobnosť, že v čakacom rade nebude ani jedna požiadavka je [2].

(2)

Z výpočtu vyplýva, že je viac ako 43% pravdepodobnosť, že hovor (požiadavka) nebude musieť čakať v čakacom rade. Pravdepodobnosť, že hovor bude čakať v čakacom rade [3] je viac ako 50%, potom sú dôležité ostatné pravdepodobnosti čakania hovorov. Podľa vzorca:

(3)

Tab. 1: Pravdepodobnosti čakania hovorov pri zaťažení ρ < 1.

k	1	2	3	4	5
pk	0,3622	0,1509	0,0419	0,0087	0,0015
k	6	7	8	9	10
pk	0,0002	0	0	0	0

Pravdepodobnosť, že v čakacom rade bude čakať jeden hovor je viac ako 36%. Pravdepodobnosť, že budú čakať dva hovory je 15%. Pravdepodobnosť čakania troch hovorov naraz v čakacom rade je viac ako 4%. Pravdepodobnosť, že budú čakať 4 a viac hovorov je menej ako 1%.

Z uvedenej Tab. 1 vyplýva, že žiadny hovor by nebol stratený. Pretože v čakacom rade sú miesta, ktoré majú pravdepodobnosť obsadenia 0%. Čiže pri takejto prevádzke a parametroch kontaktného centra sú tieto miesta v čakacom rade nevyužité. V kontaktom centre by súčasne čakalo najviac 6 hovorov a pravdepodobnosť je len 0,02%, čo je veľmi nízka pravdepodobnosť. Z uvedenej tabuľky je vyjadrená grafická reprezentácia Obr. 1.

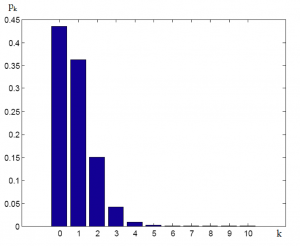
Obr. 1: Grafická reprezentácia pravdepodobnosti systému so zaťažením ρ < 1.

Pravdepodobnosť odmietnutia hovoru podľa vzorca:

(4)

Z uvedeného výpočtu vyplýva, že žiadny hovor by nebol stratený.

b) ak je systém preťažený ρ > 1

Aby došlo k preťaženiu (ρ > 1), potom intenzita vstupujúcich požiadaviek musí byť väčšia ako počet požiadaviek, ktoré systém je schopný obslúžiť (čiže platí: > μ). Parametre kontaktného centra sú z predošlého zadania, ale vstupný tok požiadaviek je 8000 hovorov za hodinu.

Čiže parametre kontaktného centra sú: = 8000 hod., μ = 1200 hod., m = 10

Zaťaženia systému podľa vzorca (1)

(5)

Z koeficientu zaťaženia vyplýva, že systém je preťažený a to viac ako šesťkrát. Čiže dá sa predpokladať, že bude viac požiadaviek v čakacom rade. Pravdepodobnosť, že v systéme nečaká žiadna požiadavka p₀ podľa (2).

(6)

Predpoklad, že bude viac požiadaviek v čakacom rade sa potvrdil, pretože pravdepodobnosť, že v systéme nečaká žiadna požiadavka je menšia ako 1%. Pravdepodobnosť, že v systéme čaká páve k požiadaviek je daná vzorcom (3). Výsledky výpočtov pre jednotlivé k sú v tabuľke (2).

Tab. 2: Pravdepodobnosti čakania hovorov pri zaťažení ρ > 1

k	1	2	3	4	5
pk	0,0092	0,0306	0,0681	0,1134	0,1512
k	6	7	8	9	10
pk	0,1680	0,1600	0,1334	0,0988	0,0659

Grafická reprezentácia tabuľky je na Obr. 2.

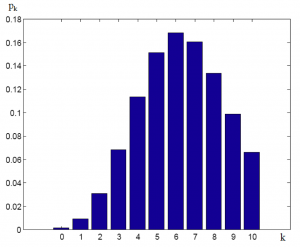
Obr. 2: Grafická reprezentácia pravdepodobnosti systému so zaťažením ρ > 1.

Z uvedeného vyplýva, že s najväčšou pravdepodobnosťou bude v systéme súčasne čakať šesť hovorov (požiadaviek). Dôležitá je posledná pravdepodobnosť p₁₀, ktorá vyjadruje pravdepodobnosť plne obsadeného systému, t.j. všetci agenti sú obsadení a aj čakací rad je naplnený. Ďalšie hovory (požiadavky), ktoré prídu v tomto momente nebudú obslúžené, ale budú odmietnuté (čiže hovory budú stratené z dôvodu preťaženia systému). Pravdepodobnosť odmietnutia hovoru podľa vzorca (4):

(4)

Pravdepodobnosť odmietnutia hovoru je 6,5%. Tu je možné optimalizovať kontaktné centrum na základe požiadaviek prevádzkovateľa.

3. Optimalizácia kontaktného centra

Všetky hodnoty pravdepodobností sú závislé od počtu prichádzajúcich volaní a na vstupných parametroch, ktoré určuje prevádzkovateľ (organizácia). Z uvedeného modelového príkladu je vidno, že pravdepodobnosť odmietnutia požiadavky je vysoká (6,5%). Pre optimalizáciu kontaktného centra, aby sa znížila pravdepodobnosť odmietnutia hovoru, je v tomto prípade potrebné zvýšiť počet agentov. Pre stanovenie počtu agentov si organizácia môže stanoviť pravdepodobnosť odmietnutia hovoru. Pre tento modelový prípad je hodnota stanovená na 1%.

Parametre systému teda sú: = 8000 hod., μ = 1200 hod., m = 10, pm = 0,01

kde m je počet agentov na začiatku optimalizácie systému a p_m je maximálna pravdepodobnosť odmietnutia hovoru. Vypočíta sa zaťaženie systému a pravdepodobnosť systému ako v predchádzajúcich prípadoch. Podľa vzorcov (1) a (2):

Zvýšením počtu agentov sa zníži pravdepodobnosť odmietnutia požiadavky. Optimalizáciu vykonáme tak, že vypočítame pravdepodobnosť odmietnutia požiadavky podľa vzorca (4) pre väčší počet agentov. Z grafu (Obr. 3) a Tab. 3 odčítame počet agentov podľa stanovenej pravdepodobnosti odmietnutia p_m.

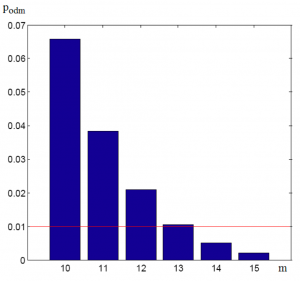
Obr. 3: Grafická reprezentácia pravdepodobnosti odmietnutia p_odm.

Tab. 3: Pravdepodobnosti odmietnutia hovoru pri zmene počtu agentov.

m	10	11	12	13	14	15
podm	0,0659	0,0384	0,0209	0,0106	0,0050	0,022

Z uvedeného vyplýva, že počet agentov by sa mal zmeniť na 14, aby pravdepodobnosť odmietnutia hovoru bola pod stanovenou hodnotou 1%. Ak kontaktné centrum bude mať 14 agentov, tak pravdepodobnosť odmietnutia hovoru je 0,5%. Pravdepodobnosť, že v systéme čaká páve k požiadaviek je daná vzorcom (3). Výsledky výpočtov pre jednotlivé k sú v Tab. 4.

Tab. 2: Pravdepodobnosti čakania hovorov pri zaťažení ρ > 1

k	1	2	3	4	5
pk	0,085	0,0284	0,0631	0,1051	0,1402
k	6	7	8	9	10
pk	0,1558	0,1483	0,1236	0,0916	0,0610
k	11	12	13	14
pk	0,0370	0,0206	0,0105	0,005

Grafická reprezentácia tabuľky je na Obr. 4

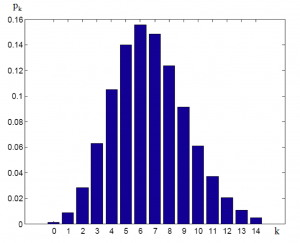
Obr. 4: Grafická reprezentácia pravdepodobnosti čakania hovorov pri zmene počtu agentov.

Z uvedeného vyplýva, že s najväčšou pravdepodobnosťou bude v systéme súčasne čakať šesť hovorov (požiadaviek). Táto pravdepodobnosť je o 1% menšia ako v predchádzajúcom modeli s desiatimi agentmi. Pravdepodobnosť p₁₄ vyjadruje pravdepodobnosť plne obsadeného systému a nadobúda hodnotu 0,5%. Ďalšie hovory (požiadavky), ktoré prídu v tomto momente, nebudú obslúžené.

Pri 13 agentoch je pravdepodobnosť odmietnutia len 1,06%, čo je veľmi blízko požadovanej hranice 1%. V praxi by sa organizácia „uspokojila“ s počtom agentov 13, pretože rozdiel v požadovanej maximálnej pravdepodobnosti od požadovanej je len 0,06%, je minimálny. Čiže kontaktné centrum organizácií splní tú istú funkciu ako kontaktné centrum so 14 agentmi. Organizácia ušetrí na nákladoch pri prevádzkovaní kontaktného centra, a to práve na tomto jednom agentovi.

4. Zhodnotenie

Kontaktné centrum je pre organizáciu veľkým prínosom, ale musí byť dobre navrhnuté. Kontaktné centrum sa riadi podľa určitého modelu hromadnej obsluhy. Týchto modelov je veľké množstvo. V tomto prípade je to model systému M/M/m/K. Modelovaním kontaktného centra pomocou tohto modelu sme vypočítali pravdepodobnosti čakania určitého počtu hovorov v čakacom rade. Ďalším dôležitým vypočítaným parametrom je pravdepodobnosť odmietnutia hovoru. Z výpočtu pri zaťažení systému ρ < 1 je pravdepodobnosť odmietnutia veľmi nízka.

Ak sa zaťaženie systému zvýši, preťaží, tak sa pravdepodobnosť odmietnutia zvýši. Preťažený systém je nevhodný, preto ho treba optimalizovať, či už technickým riešením (inovácia hardvéru), alebo personálnym – zvýšenie počtu agentov. Pri optimalizovaní kontaktného centra sa podľa stanovenej pravdepodobnosti odmietnutia dopočítal počet agentov. V našom prípade je optimálny počet agentov 14.

Ďalšími charakteristickými parametrami kontaktného centra sú čas čakania požiadavky v čakacom rade, celkový čas vybavenia požiadavky. Tieto hodnoty sú dôležité z pohľadu zákazníka, pretože ich reálne vníma. Prevádzkovateľ kontaktného centra sa snaží optimalizovať kontaktné centrum. Snaží sa minimalizovať čas čakania na obsluhu a minimalizovať náklady na kontaktné centrum. Tieto protichodné procesy treba citlivo vyvážiť tak, aby boli uspokojené požiadavky na obsluhu, ale aj prevádzkovateľ.

5. Odkazy na literatúru

1. Hayes J. F., Babu T. J. V. G., “Modeling and analysis of telecommunications networks”, ISBN 0-471-34845-7 2004
2. G., Greiner S., Meer H., Trivedi K. “Queing Networks and Markov Chain“, 2006
3. Polec J., Karlubíková T., Vargic R. “Pravdepodobnostné modely v telekomunikáciách“, ISBN 978-80-227-2641-2, 2006

---

Spoluautor článku je Ing. Erik Chromý, PhD., Katedra mikroelektroniky, Fakulta Elektrotechniky a Informatiky, Slovenská Technická Univerzita, Ilkovičova 3, Bratislava 812 19

---

Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Telekomunikácie I., ISBN 978-80-227-3508-7