Pri projektovaní elektromechanických prvkov namáhaných či už tepelne, elektricky alebo mechanicky je veľmi vhodnou a v poslednej dobe čoraz častejšie využívanou metódou MKP (Metóda konečných prvkov). Pomocou softvéru postaveného na jej základe možno vykonať numerické simulácie pre rôzne zaťažovacie stavy. Cieľom tohto článku je poskytnúť prehľad bezskrutkových elektrických kontaktov využívaných v elektrotechnických zásuvkách avidliciach. Bol vytvorený CAD model bezskrutkového kontaktu, na ktorom boli vykonané výpočty elektrického a teplotného poľa s MKP pre rôzne okrajové podmienky a zaťažovacie stavy.

1. Úvod

Modelovanie a simulácia sú veľmi široké pojmy a v rôznych vedných odboroch si ľudia pod nimi predstavujú rôzne skutočnosti. V technickej inžinierskej praxi, v závislosti od vedného odboru, sa pod pojmami modelovanie má na mysli modelovanie procesov, dejov, vytváranie CAD modelov súčiastok alebo vyhotovenie modelov v určitej mierke a ich skúmanie. V strojárskom i elektrotechnickom odbore sa často stretávame s návrhmi súčiastok, ktorých vlastnosti musia byť preskúmané ešte skôr ako budú tieto súčiastky reálne vytvorené.

To, či daný návrh súčiastky spĺňa požiadavky ako napr. tepelnú odolnosť súčiastky sa preveruje pomocou CAD/CAE modelov a ich simuláciami [1]. Medzi systémy určené pre kon- štruovanie prototypov možno zaradiť I-DEAS, PRO/I, CATIA, SOLID EDGE. Akýkoľvek fyzikálny problém môžeme na základe všeobecných zákonitostí matematicky zapísať diferenciálnymi, integrálnymi alebo variačnými rovnicami, ktoré však analyticky riešiť nevieme, alebo len veľmi ťažko. Z toho dôvodu sa na riešenie používajú rôzne numerické metódy, z ktorých medzi najznámejšie vinžinierskej praxi patrí metóda konečných prvkov – MKP (Finite element method – FEM).

Je to počítačovo orientovaná metóda, ktorá má oproti ostatným množstvo výhod. Jej podstata spočíva v diskretizovaní skúmanej oblasti na malé podoblasti – elementy (prvky) tvorené uzlovými bodmi (nodmi). Tieto programy, medzi ktoré patrí aj ANSYS, využívaju analógiu riešenia úloh mechaniky kontinua a sú stavané univerzálne, t. j. užívateľ v podstate analogickým postupom, mnohokrát aj rovnakými príkazmi, rieši úlohy z mechaniky telies, prenosu tepla, prúdenia, akustiky, elektromagnetického poľa a pod.

2. Bezskrutkový spoj

Norma STN EN 60309-1 definuje dva základné typy bezskrutkových spojení: 1.) bezskrutková svorka (screewless type terminal) – svorka na pripojenie a následne odpojenie jedného alebo viacerých vodičov, pričom pripojenie sa vykonáva priamo alebo nepriamo inými prostriedkami ako skrutkami. 2.) svorka prerážajúca izoláciu (insulation piercing terminal – IPT) – svorka na pripojenie anásledne odpojenie jedného alebo viacerých vodičov, pričom pripojenie sa vykonáva prepichnutím, prevŕtaním, prerezaním, odstránením, posunutím izolácie vodiča (vodičov) alebo iným spôsobom bez predchádzajúceho odizolovania [2].

Vzhľadom na jednoduchú manipuláciu stakýmito kontaktmi sa ich použitie čoraz viacej rozširuje. Takmer každý výrobca používa svoj vlastný, istým spôsobom špecifický a originálny spôsob bezskrutkového spojenia. Aby boli výrobky konkurencieschopné na trhoch a firmy nezaostávali za inými, musia spĺňať všeobecné štandardy a samozrejme vybrané technické normy. To je úloha pre konštruktérov, inžinierov a dizajnérov už v priebehu návrhu.

Pochopiteľne, jednotlivé firmy si svoje „know- how“ dobre strážia, a aj právne chránia patentmi. Medzi popredných výrobcov vtejto oblasti patria: WAGO – r.1951– PUSHWIRE technológia, r. 1977- Cage Clamp (podstatu tejto pružiny využíva aj nami vytvorený model od SEZ Dolný Kubín), BALS Elektrotechnic – Quick Connect, PCE Electric – Turbo Twist, SCAME, MERLIN GERIN, MENNEKES Elektrotechnik, WALTHER Electric a iné.

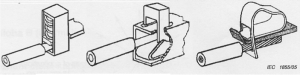
Obr. 1 Bezskrutkové svorky [2]

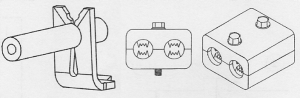
Obr. 2 Svorky prerážajúce izoláciu [2]

3. Modelovanie a analýza

Táto časť postupne rozoberá jednotlivé kroky vytvorenia modelu bezskrutkovej vidlice vybranej zásuvky, pričom detailnejšie informuje práve o bezskrutkovom kontakte. V simulácii zachytáva priebeh teplotného a elektrického poľa v prípade ustáleného stavu (steady state) idealizovaného styku vodiča so svorkou.

3.1 Fyzikálny model

Aby sme mohli náš skúmaný objekt podrobiť elektrotepelnej analýze MKP v programe ANSYS [3] je nevyhnutné vytvoriť jeho model zodpovedajúci reálnej súčiastke. Napriek tomu, že samotný ANSYS ponúka možnosť modelovať, veľmi zložité priestorové modely sa vytvárajú v CAD/CAE systémoch, ktoré bývajú zo simulačnými programami prepojené, pomocoukompatibilných formátov (iges, parasolid a iné). Rovnako sa na analýzy zložitejších geometrií využíva nadstavba klasického ANSYS-u ANSYS Workbench, ktorý taktiež ponúka používateľovi omnoho jednoduchšie a prívetivejšie rozhranie.

3.2 Geometria

Zostava našej súčiastky bola vytvorená softwérom SOLID EDGE V17 [4]. Konkrétne ide o bezskrutkovú vidlicu LeaderPlus, ktorá má katalógové označenie IVB 1653 – 16 A 400 V IP44, a je pomerne novým produktom spoločnosti SEZ Dolný Kubín.

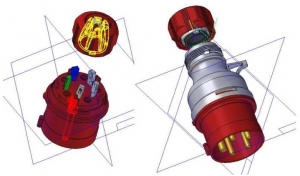
Obr. 3. Model bezskrutkovej vidlice vytvoreny v programe SOLID EDGE

Ako vidieť geometria celej vidlice, norovnako aj bezskrutkového spoja, je značne komplikovaná a vytvorenie takého modelu si vyžaduje veľa práce a trpezlivosti. Ztoho dôvodu sme vytvorili len model spojenia pre plný 1,5 mm² CY vodič a štandardný fázový kolík, ana tomto modeli boli vykonané simulácie.

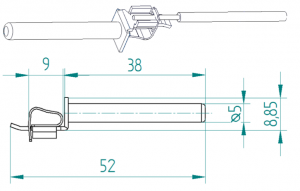
Obr. 4 Model bezskrutkového kontaktu vytvorený v programe SOLID EDGE

3.3 Materiálové vlastnosti

Pri riešení inžinierskych úloh pomocou MKP musíme v prvom rade poznať materiály jednotlivých častí modelu a pre ne poznať ich konkrétne materiálové vlastnosti (material models), pričom práve typ simulovaného poľa, určuje, ktoré materiálové vlastnosti je potrebné definovať. Vzhľadom na to, že riešime stacionárnu previazanú elektro-tepelnú úlohu (thermal – electric steady state), musíme poznať:

• λ – koeficient tepelnej vodivosti materiálu [W.m^-1.K^-1]
• ρ – rezistivitu [Ωm] (konduktivita [Sm^-1], s = 1/ ρ )

Je nutné poznamenať, že tieto fyzikálne vlastnosti značne závisia od teploty. Pri menších zmenách teploty je možné túto skutočnosť zanedbať a uvažovať hodnoty pri bežných izbových podmienkach t.j. 20 – 25oC. Hodnoty špecifickej tepelnej vodivosti λ pri rôznych teplotách bývajú uvádzané v termodynamických tabuľkách [5]. Rezistivity pri rôznych teplotách dopočítame podľa vzťahu:

(1)

kde ρ₀ [Ωm] – rezistivita pri vzťažnej teplote T₀, α [K^-1] – teplotný súčiniteľ elektrického odporu (α Cu = 0,005) – zmena teploty voči vzťažnej teplote T0.

Napríklad pre meď: ρ_Cu100 = 1,68.(1 + 0,005.75) = 2,31 Ωm .10^-8.

Tab.1 Materiálové vlastnosti častí použitých v kontakte

materiál		λ [W.m-1.K-1]		ρ [Ωm.10-8]
		25 oC	100 oC	25 oC	100 oC
1	CuZn37	121,4	125,9	7,1	9,76
2	a ß mosadz	111	119	7,8	10,73
3	med	383	379	1,68	2,31
4	PVC	0,19		108- 1010 Ωm

3.4 Generovanie siete

Generovanie siete (meshing) predstavuje generovanie uzlov a elementov. Táto časť býva vykonávaná programami nazývanými generátory siete, ktoré sú zvyčajne súčasťou programov MKP. Presnosť numerického riešenia závisí od počtu a veľkosti prvkov modelu. V zásade platí, čím viac prvkov, tým väčšia presnosť výsledkov. Ale na druhej strane zvyšovanie počtu elementov, predlžuje celkový čas potrebný pre výpočet. Veľkosť hrany nášho elementu bola prednostne volená d = 5.10^-4 m a celkový počet prvkov bol 40 000 – 50 000.

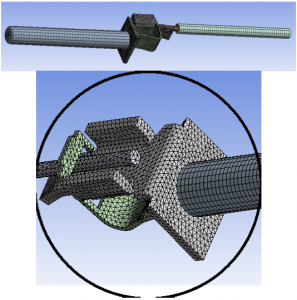
Obr. 5 Výsledny vysieťovany model a detail spoja v programe ANSYS Workbench

3.5 Okrajové podmienky

Pri riešení simulácií, je potrebné definovať okrajové podmienky, ktorými v našom prípade sú: veľkosť pretekajúceho prúdu [A], napätie [V], odvod tepla konvekciou [α, T ∞ + zadať plochy konvekcie]. Na obrázku 6 možno vidieť jednotlivé okrajové podmienky ako boli zadané na náš model. Veľkosť napätia je stála U = 230 V, pričom bola definovaná práve na koncovú plochu kolíka, kde býva privedené napätie(plocha A).

Z definície efektívnej hodnoty striedavého prúdu vyplýva, že má rovnaké tepelné účinky ako prúd jednosmerný o tej istej veľkosti. Preto sme mohli prúd zadávať ako jednosmerný, a to na vstupnú plochu vodiča v rozpätiach I = 1 – 16A (plocha B). Nažlto sú vyfarbené plochy odvodu tepla. Sú to všetky vonkajšie plochy okrem krajných, ktoré považujeme za tepelne zaizolované. Teplotu okolia sme preddefinovali na nemenných T∞ = 30°C, pretože oteplenie norma definuje ako rozdiel výslednej teploty a teploty okolia pri 30°C. Koeficient konvekcie α sme menili v rozmedziach 2 – 12 W.m^-2.K^-1, aby sme zistili ako sa náš model správa pri rôznych hodnotách.

Obr. 6 Definovanie okrajových podmienok

3.5 Idealizácia modelu

Naša simulácia rieši výpočet previazaného elektro- tepelného poľa bezskrutkového kontaktu v zjednodušenej podobe. To znamená zanedbanie prechodového elektrického i tepelného odporu kontaktu medeného vodiča s mosadznou svorkou. Simuluje ustálený stav (steady state) elektrického a teplotného poľa. V takýchto prípadoch máva nezastupiteľné miesto experiment a veľkosť prechodového je v prípade potreby možné merať, napr. klasickou volt-ampérovou metódou.

Takéto meranie má veľký význam, vzhľadom na to, že logicky najväčšie oteplenie vzniká práve v mieste kontaktu, a určite je to výzva do budúcna pre podrobnejší a presnejší rozbor tejto úlohy. V našich simuláciách tento prechodový odpor neuvažujeme. Kontakt medzi vodičom a svorkou je maximálne zidealizovaný a síce uvažujeme s líniou (čiarkou) styku resp. veľmi malou obdĺžnikovou plôškou, čím dosiahneme, aby toto miesto styku bolo zhľadiska tepelného aj prúdového zaťaženia čo najnepriaznivejšie.

4. Vyhodnotenie simulácii

Všetky úlohy sa riešili ako stacionárne, tzn. hľadáme ustálený stav skúmaných fyzikálnych polí. Výsledky analýz podáva Postprocessor programu MKP vo forme tabuliek, grafov, a grafických máp (izočiary, izoplochy, atď.). Pre nás sú zaujímavé všetky veličiny, ktoré sa týkajú nami skúmaných polí: teplota [^oC], tepelný tok [W/m²], elektrické napätie [V], intenzita elektrického poľa [V/m], prúdová hustota [A/m²], Jouleovo teplo [W/m³].

Prvá séria simulácií (Tab.2) predstavuje závislosť výsledných maximálnych teplôt nášho modelu pri parametrickom zvyšovaní prúdu pre tri rôzne hodnoty koeficientov α = konšt. Grafická závislosť od prúdu prebieha kvadraticky, a s narastajúcim prúdom prudko stúpa (Obr. 7).

Tab. 2 Tabuľka odsimulovaných hodnôt maximálnej teploty pre idealizovaný model

I[A]	α [Wm-2K-1]
	7	5	2
	tmax [oC]
1	30,1	30,1	30,2
2	30,3	30,4	30,9
4	31,2	31,6	33,9
6	32,8	33,8	39,1
8	35,5	36,8	46,7
10	37,9	40,9	57,5
12	41,7	46,0	71,9
14	46,2	52,5	91,5
16	51,8	60,3	113,4

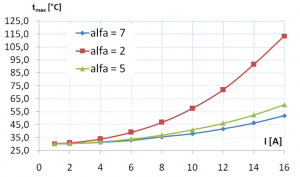
Obr. 7 Grafická závislosť maximálnej teploty od pretekajúceho prúdu pre idealizovaný model

Predmetom ďalšej simulácie (Tab.3) bol konštantny prúd I = konšt, a tento raz sme menili koeficient konvekcie. Z tohto riešenia je opäť vynesená graficka závislost (Obr.8). V prípade stáleho prekročenia prípustnej teploty môže dôjsť k zvýšenej korózii, zníženiu životnosti izolačných častí, v krajných prípadoch až k porušeniu mechanickej pevnosti vodivých častí.

Norma povoľuje maximálne oteplenie pri normálnej prevádzke = 50 K. Zistili sme, že pri maximálnych prúdoch, a najnepriaznivejších podmienkach konvekcie sú tieto hodnoty hraničné, alebo dokonca o niekoľko stupňov prekročené. Preto treba upozorniť na možnosť vzniku nadmerného oteplenia. Pri interpretácii výsledkov, však treba vždy zohľadniť a prihliadať na uvažované okrajové podmienky. Tie sú v teplotnom poli iba veľmi ťažko definovateľné, najmä čo sa týka odvodu tepla konvekciou [6].

Tab. 3 Tabuľka Tabuľka odsimulovaných hodnôt maximálnej teploty pre idealizovaný model v závislosti od podmienok konvekcie

α [Wm-2K-1]	I[A]
	8	12	16
	tmax [oC]
2	46,7	71,9	113,4
3	41,2	56,9	82,9
4	38,4	50,0	68,3
5	36,8	46,0	60,3
7	35,5	41,7	51,8
9	34,1	39,4	46,5
12	33,7	38,1	44,2

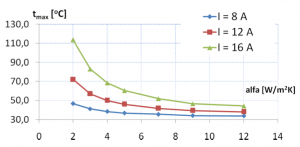
Obr. 8 Závislosť maximálnej teploty od koeficientu prestupu tepla pre idealizovaný model

Na obrázku 9 je znázornené teplotné pole v modeli. Zmeny teploty sú kontinuálne, v mieste kontaktu sa teplota jemne zvýši. Dokazuje to aj fakt, že v tomto mieste vznikajú najväčšie Joulove straty, pretože v tomto miesto je sústredená najväčšia prúdová hustota (Obr.11). Vzhľadom na to, že v ustálenom stave je odvod tepla prúdením dostatočne veľký, nie je táto skutočnosť na výslednej farebnej škále výraznejšie pozorovateľná. Napäťový úbytok pri modeli, ktorý neuvažuje prechodový odpor kontaktu pri všetkých okrajových podmienkach je = 10 mV. Norma dovoľuje 22,5 mV.

Obr. 9 Výsledné teplotné pole bezskrutkovej svorky (I=16A,α=7Wm^-2K^-1)

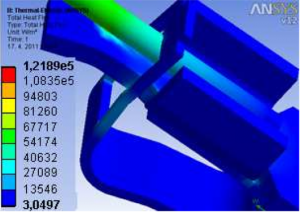
Obr. 10 Výsledný tepelný tok [W/m²] bezskrutkovej svorky ( I = 16A, α = 3 Wm^-2K^-1)

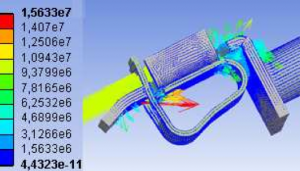
Obr. 11 Prúdová hustota [Am^-2] vykreslená vektorovo ( I = 16A,α = 3 Wm^-2K^-1)

5. Záver

Cieľom tohto príspevku bolo prostredníctvom metódy konečných prvkov analyzovať elektro-tepelné pole bezskrutkového kontaktu. Článok prináša krátku charakteristiku bezskrutkových spojení a poskytuje rešerš súčasných spojení tohto typu. Praktická časť sa zaoberá vymodelovaním 5-pólovej trojfázovej vidlice, a simuláciami na jej bezskrutkovom kontakte, pre rôzne zaťažovacie stavy. V programe Solid Edge bol vytvorený model, ktorý bol implementovaný do ANSYS Workbench.

Náš model bol zidealizovaný a podrobený stacionárnym analýzam. Výsledky boli zhodnotené a boli prijaté závery z hľadiska nadmerného oteplenia. Vzhľadom na to, že sme sa zaoberali iba zjednodušeným modelom, ktorý zanedbával prechodový odpor, určite sa nám otvárajú dvere do budúcna pre podrobnejšie multifyzikálne analýzy a optimalizácie, či už konkrétne tejto úlohy, alebo problémov podobného typu.

Použitá literatúra

1. KUTIŠ, V.: Základy modelovania a simulácie. FEI STU, Bratislava 2006
2. STN EN 60309-1: Vidlice, zásuvky a zásuvkové spojenia na priemyselné použitie. Slovenský ústav technickej normalizácie, Bratislava 2005
3. ANSYS 12. A general purpose FEM program, 2011
4. SOLID EDGE V17. UGS PLM software, 2005
5. RAŽNIEVIČ, K.: Tepelné tabuľky a diagramy. 1. vyd. Bratislava ALFA 1969. ISBN 63-091-68-05
6. GEBURA,P .: Multifyzikálna analýza bezskrutkového kontaktu. Diplomová práca. FEI STU, Bratislava 2007
7. MURÍN, J.: Manuskript prednášok, Riešenie teplotného poľa pomocou MKP. Katedra mechaniky. FEI STU

---

Spoluautorom článku je prof. Ing. Justín Murín, DrSc., Katedra mechaniky, Fakulta Elektrotechniky a Informatiky, Slovenská Technická Univerzita, Ilkovičova 3, Bratislava 812 19

---

Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Aplikovaná mechanika a získala cenu IEEE, ISBN 978-80-227-3508-7