Základ vybudovania úspešného kontaktného centra tvorí správny model a z neho vychádzajúci následný návrh systému. Prílišná zložitosť modelu môže byť niekedy kontraproduktívna. Hlavným cieľom tejto práce je analyzovať možnosti Markovovského modelu M/M/m/∞ v prostredí kontaktného centra. Tento model ponúka širokú škálu výpočtov dôležitých prevádzkových parametrov systému, pričom si zachováva prehľadnú a jednoduchú štruktúru, čo môže byť kľúčovým faktorom pri návrhu kontaktného centra.

1. Úvod

Základným predpokladom úspechu spoločnosti poskytujúcej akýkoľvek druh služieb na trhu je vybudovanie dobrých vzťahov so svojimi zákazníkmi. Kľúčovým faktorom je udržiavanie stáleho kontaktu so zákazníkom. Jedným zo spôsobov umožňujúcich jednoduchý a pritom veľmi efektívny kontakt so zákazníkmi je vybudovanie kontaktného centra. Kontaktné centrum je zložitý komunikačný systém, ktorý vzniká ako nadstavba pobočkovej ústredne a ponúka spoločnosti komplexný systém pre komunikáciu so zákazníkom, či už prostredníctvom telefónneho hovoru, e-mailu alebo napríklad aj textového chatu s pracovníkom kontaktného centra.

Matematicky popísať takýto zložitý systém je veľmi náročné. Preto sa v ďalšej časti textu pod pojmom kontaktné centrum rozumie systém určený len na spracovanie telefónnych hovorov. Takto zjednodušený systém dokonale vyhovuje účelom tejto práce.

2. Kontaktné centrum ako systém hromadnej obsluhy

Systém, kde určité množstvo obslužných staníc obsluhuje veľké množstvo požiadaviek sa nazýva systém hromadnej obsluhy (SHO). Takýmto systémom je aj kontaktné centrum. V tomto prípade tvoria požiadavky zákazníci telefonujúci do kontaktného centra a obslužné stanice reprezentujú agenti kontaktného centra, ktorých úlohou je riešiť požiadavky zákazníkov. Všeobecný príklad systému hromadnej obsluhy je znázornený na obr. 1.

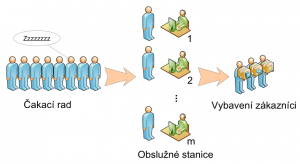
Obr. 1. Systém hromadnej obsluhy.

Nech systém na obr. 1 je kontaktné centrum, v ktorom sa nachádza m obslužných staníc, čiže m agentov. Požiadavky tohto systému vytvárajú telefonujúci zákazníci, ktorí telefonujú do kontaktného centra náhodne a nezávisle jeden od druhého. Agenti obsluhujú telefonujúcich zákazníkov po jednom a v prípade, že sú všetci agenti zaneprázdnení, musia ďalší telefonujúci zákazníci čakať na uvoľnenie agenta v čakacom rade. Čas obsluhy hovoru je náhodný a nezávisí od času obsluhy iných hovorov. V takomto prípade je možné toto kontaktné centrum označiť ako stochastický systém hromadnej obsluhy.

Štatistickým sledovaním sa ukázalo, že spôsob príchodu telefónnych hovorov do kontaktného centra napodobňuje Poissonovo rozdelenie náhodnej premennej, čas obsluhy hovoru ilustruje exponenciálne rozdelenie [1]. Správanie sa takéhoto systému je možné úspešne opísať pomocou Markovovských procesov.

3. Markovovské procesy

Markovovské procesy poskytujú flexibilný a veľmi účinný nástroj, pre opis a analýzu dynamických vlastností stochastických SHO [2, 3].
Nech T = {t₀, t₁, … , t_n} je množina rôznych časov, pričom 0 = t₀ < t₁ < … < t_n a nech S = {s₁, s₂, … , s_m} je množina všetkých stavov, v ktorých sa môže nachádzať systém v rôznych časoch, potom takýto systém je možné opísať pomocou Markovovských procesov, ak platí (1):

(1)

čiže pravdepodobnosť, že systém sa v čase t_n+1 nachádza v stave s_n+1, závisí len od toho, že v čase tn sa systém nachádzal v stave sn a nezávisí od toho v akých stavoch a v akých časoch sa systém nachádzal pred časom tn [2]. Vo voľnom preklade táto základná Markovovská vlastnosť znamená, že budúcnosť závisí len od prítomnosti a minulé stavy systému netreba brať vôbec do úvahy.

4. Markovovský model M/M/m/∞

Z veľkého množstva Markovovských modelov SHO je možné pre každý systém zvoliť ten najvhodnejší model podľa rôznych kritérií (komplexnosť, výpočtová náročnosť a pod.). Ďalšia časť práce sleduje možnosť využitia Markovovského modelu M/M/m/∞ v prostredí kontaktného centra.

Podľa Kendallovej klasifikácie systémov hromadnej obsluhy [3, 4], znamená označenie modelu M/M/m/∞: M – Poissonov proces príchodov (vstupov) požiadaviek do systému, /M – exponenciálne rozdelenie času obsluhy, /m – počet serverov (agentov), /∞ – nekonečná populácia požiadaviek systému a rovnako neobmedzená kapacita čakacieho radu.

4.1. Základné predpoklady modelu

Nech λ vyjadruje strednú hodnotu rýchlosti príchodu požiadaviek do systému a μ nech vyjadruje priemernú rýchlosť obsluhy požiadaviek, pričom priemerný čas obsluhy jednej požiadavky je T_obs = 1/μ. Grafické znázornenie systému M/M/m/∞ je zobrazené na obr. 2.

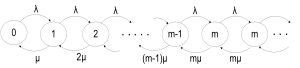
Obr. 2. Markovovský model M/M/m/∞.

Z obr. 2 je možné vidieť správanie sa systému, požiadavky prichádzajú náhodne, s Poissonovským rozdelením so strednou hodnotou λ, tieto požiadavky sú obsluhované, pričom čas obsluhy je náhodný a je možné opísať ho exponenciálnym rozdelením s mierou μ. Systém sa teda zapĺňa s rýchlosťou λ (rýchlosť prechodu zo stavu k do stavu k+1, kde k je počet požiadaviek v systéme). Naopak, systém sa vyprázdňuje rýchlosťou kμ (zo stavu k do k-1).

Toto správanie sa systému platí do stavu k ≤ m, v prípade, že v systéme je viac požiadaviek k ako agentov m, agenti dokážu požiadavky obsluhovať len rýchlosťou mμ a každá ďalšia prichádzajúca požiadavka do systému je nútená čakať na uvoľnenie agenta v čakacom rade, tento čakací rad má nekonečnú kapacitu.

4.2. Výpočtová kapacita modelu

Využitím základných rovníc Markovovského modelu M/M/m/∞ a ich určitými úpravami je možné vypočítať veľké množstvo dôležitých prevádzkových parametrov kontaktného centra [2, 3, 4, 5]. Stabilita systému ρ je (2):

(2)

kde m je počet agentov. V systéme musí vždy platiť vzťah ρ < 1, čo znamená, že vtedy je systém stabilný. Pravdepodobnosť PQ udáva pravdepodobnosť, že telefonujúci zákazník bude musieť čakať na uvoľnenie agenta v čakacom rade (3):

(3)

kde P₀ vyjadruje pravdepodobnosť, že systém je prázdny (4):

(4)

Priemerný počet požiadaviek v celom systéme je N (5):

(5)

Požiadavka strávi v systéme priemerný čas T (6):

(6)

Priemerný počet požiadaviek čakajúcich v čakacom rade Q je daný (7):

(7)

pričom požiadavka strávi v čakacom rade priemerný čas W (8):

(8)

Z definície veličín λ a μ vychádza vzťah (9):

(9)

kde, A predstavuje prevádzkové zaťaženie systému udávané v Erlangoch. Dosadením (9) do (2) a následným dosadením (2) do (3) a (4) a úpravou rovníc dostávame (10):

(10)

Rovnica (10) sa nazýva Erlangova C rovnica [1], pričom PC predstavuje pravdepodobnosť, že požiadavka musí na obsluhu čakať v čakacom rade. Je zrejmé, že rovnice (3) a (10) sú rovnaké, čím je dokázané, že tieto dva systémy sú identické a jedným systémom možno dopĺňať druhý. Využitím tohto poznatku a rozšírením Erlangovho modelu o parameter GoS (Grade of Service), udávajúci stupeň poskytovaných služieb [1, 6], je možné výpočtovú kapacitu modelu M/M/m/∞ rozšíriť aj o tento parameter (11):

(11)

kde GoS vyjadruje vlastne percento prichádzajúcich hovorov, ktoré sú prijaté na obsluhu agentom do zvoleného času T_W.

5. Výpočet dôležitých prevádzkových parametrov kontaktného centra

Pre správny návrh kontaktného centra je dôležité čo najpresnejšie odhadnúť základné prevádzkové parametre kontaktného centra, a to priemernú rýchlosť príchodu telefónnych hovorov do systému a priemerný čas obsluhy jedného hovoru. Ak nie je uvedené inak, všetky výpočty prevádzkových parametrov kontaktného centra sa odvíjajú od základných hodnôt:

• λ = 60 prichádzajúcich hovorov za hodinu,
• čas obsluhy jedného hovoru je T_obs = 5 minút.

Z (9) teda vyplýva, že priemerné prevádzkové zaťaženie takéhoto kontaktného centra je 5 Erl.

5.1 Výpočet potrebného počtu agentov

Základný prevádzkový parameter potrebný pri návrhu kontaktného centra je potrebný počet agentov. Pri správne odhadnutých hodnotách λ a T_obs je výpočet potrebného počtu agentov podľa rovnice (3) pomerne jednoduchý. Na obr. 3 je graf závislosti pravdepodobnosti čakania v čakacom rade od rastúceho počtu agentov. Nech maximálna pravdepodobnosť P_Q v modelovanom kontaktom centre nepresahuje 5 %. Z obr. 3 ako aj z tab. 1 je jasné, že prvý vyhovujúci počet agentov pre túto podmienku je m = 10.

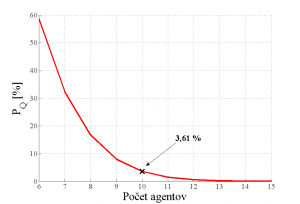
Obr. 3. Graf závislosti P_Q [%] od počtu agentov.

Z obr. 3 je možné ďalej vidieť, že pri počte agentov 10 je priemerná hodnota pravdepodobnosti P_Q = 3,61 %. Táto hodnota znamená, že zo 100 telefonujúcich zákazníkov do kontaktného centra, musia v čakacom rade čakať menej ako štyria zákazníci. Ďalšie hodnoty prevádzkových parametrov kontaktného centra pri rôznom počte agentov sú uvedené v tab. 1.

Tab. 1. Prevádzkové parametre pri A = 5 Erl.

m	PQ [%]	N	T [min]	Q	W [min]	GoS [%]	ρ
8	16,73	5,28	5,28	0,28	0,28	87,61	0,63
9	8,05	5,10	5,10	0,10	0,10	94,60	0,56
10	3,61	5,04	5,04	0,04	0,04	97,81	0,50
11	1,51	5,01	5,01	0,01	0,01	99,17	0,45
12	0,59	5,00	5,00	0,00	0,00	99,71	0,42

Z tab. 1 vidieť, že pri prevádzkovom zaťažení A = 5 Erl a pri počte agentov m = 10 je GoS = 97,81 %. Táto hodnota znamená, že zo 100 prichádzajúcich hovorov do kontaktného centra menej ako 3 hovory čakajú na obslúženie dlhšie ako čas T_W = 30 sekúnd.

Poznámka 1: V tab. 1 je možné vidieť, že prevádzkové parametre N, T a Q, W dosahujú rovnaké číselné hodnoty. Je potrebné pripomenúť, že λ = 60. V Markovovskom modeli M/M/m/∞, rovnako ako aj v rôznych iných systémoch hromadnej obsluhy platí vzťah (12):

(12)

V originálnom výpočte sú všetky časy, s ktorými sa v práci počíta vyjadrené v hodinách. Pre lepší prehľad sú v tab. 1 časy T a W prepočítané na minúty, čiže vynásobené číslom 60, čo je zhodou okolností aj hodnota λ. Vzťah (12) sa nazýva Littleho zákon, ktorý hovorí, že priemerný počet požiadaviek v systéme je rovný priemernému času, ktorý strávi požiadavka v systéme vynásobený priemernou rýchlosťou príchodu požiadaviek do systému [2, 5, 7].

5.2 Prevádzkové parametre pri meniacom sa prevádzkovom zaťažení

Po určení potrebného počtu agentov (m = 10) je potrebné analyzovať vlastnosti navrhnutého kontaktného centra pri rôznom prevádzkovom zaťažení. V prvom rade je dôležité vedieť, aké prevádzkové limity má navrhnuté kontaktné centrum. Základnú predstavu o týchto limitoch ponúka obr. 4. Z grafu závislosti P_Q [%] od A [Erl] vidieť, že s rastúcim prevádzkovým zaťažením prudko rastie aj pravdepodobnosť, že zákazník bude musieť na vybavenie svojho hovoru čakať v čakacom rade.

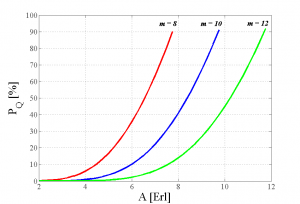
Obr. 4. Graf závislosti P_Q [%] od A [Erl].

Pre porovnanie sú v grafe na obr. 4 znázornené aj závislosti PQ [%] od A [Erl] pre systémy s počtom agentov 8 a 12. Ešte lepšiu predstavu o správaní sa modelovaného kontaktného centra ponúkajú grafy znázornené na obr. 5 a obr. 6.

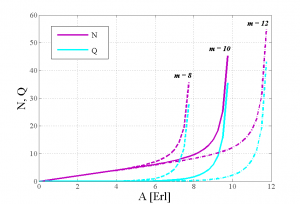
Obr. 5. Závislosť počtu požiadaviek v systéme/rade od A [Erl].

Z grafu závislostí priemerného počtu požiadaviek v systéme, resp. v rade od prevádzkového zaťaženia na obr. 5 vidieť, že spočiatku rastie počet požiadaviek relatívne mierne a takmer lineárne, až dokým nedosiahne hodnota prevádzkového zaťaženia „bod zlomu“, od tohto bodu je už rast veľmi prudký. Rovnaký bod zlomu je možné vidieť aj na grafe závislostí priemerného času, ktorý strávi požiadavka v systéme, resp. v rade, od prevádzkového zaťaženia na obr. 6.

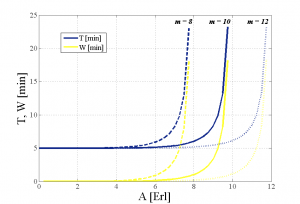
Obr. 6. Závislosť priemerného času, ktorý strávi požiadavka v systéme/rade [min] od A [Erl].

Poloha bodu zlomu udáva maximálne prevádzkové zaťaženie, ktoré je kontaktné centrum schopné zvládnuť bez zmeny počtu agentov, prípadne času obsluhy. Z obr. 5 a obr. 6 vidieť, že bod zlomu predstavuje pre kontaktné centrum s počtom agentov m = 10 a priemerným časom obsluhy hovoru T_obs = 5 minút hodnota A = 9 Erl. Presné hodnoty sú uvedené v tab. 2. Prevádzkové zaťaženie 9 Erl znamená 108 prichádzajúcich hovorov za hodinu, pri priemernom čase obsluhy jedného hovoru 5 minút.

Tab. 2 Prevádzkové parametre pri m = 10.

A [Erl]	λ	PQ [%]	N	T [min]	Q	W [min]	mpotr
4	48	0,88	4,01	5,01	0,01	0,01	9
5	60	3,61	5,04	5,04	0,04	0,04	10
6	72	10,13	6,15	5,13	0,15	0,13	11
7	84	22,17	7,52	5,37	0,52	0,37	13
8	96	40,92	9,64	6,02	1,64	1,02	14
9	108	66,87	15,02	8,34	6,02	3,34	15

V tab. 2 je zahrnutý aj parameter m_potr, tento parameter hovorí o potrebnom počte agentov pri danom prevádzkovom zaťažení pre zachovanie maximálnej pravdepodobnosti P_Q pod úrovňou 5%.

Poznámka 2: Rovnako ako v tab. 1 aj v tab. 2 dosahujú prevádzkové parametre N, T a Q, W rovnaké číselné hodnoty pri λ = 60. Aj tu platí Littleho zákon (12) opísaný v poznámke 1.

6. Kontaktné centrum ako viacfázový systém hromadnej obsluhy

Predchádzajúca časť práce sa zaoberala kontaktným centrom ako systémom, kde prichádzajúce hovory obsluhovali priamo agenti kontaktného centra, prípadne tieto hovory čakali na uvoľnenie agenta v čakacom rade. V skutočnosti sa často vyskytuje kontaktné centrum, kde prvý kontakt so zákazníkom vykonáva tzv. jednotka interaktívnej hlasovej odpovede (Interactive Voice Response Unit), skrátene IVR [7].

IVR má za úlohu identifikovať volajúceho zákazníka, zistiť základnú povahu jeho problému a následne prepojiť hovor priamo na najkvalifikovanejšieho agenta pre vyriešenie daného problému. Týmto sa efektívne skráti čas obsluhy hovoru o čas, ktorý musí agent venovať na začiatku hovoru identifikácii zákazníka a určeniu podstaty problému.

V niektorých prípadoch je jednotka IVR schopná priamo obslúžiť telefonujúceho zákazníka, bez potreby akéhokoľvek zásahu agenta do hovoru. Modelovať kontaktné centrum s IVR ako jeden systém je veľmi zložité, je na to potrebná široká škála zložitých štatistických výpočtov a detailná znalosť Markovovských procesov [8]. Jednoduchším spôsobom je využitie problematiky viacfázového systému hromadnej obsluhy (obr. 7).

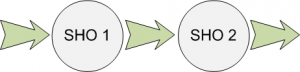
Obr. 7. Viacfázový systém hromadnej obsluhy.

Nech SHO 2 je doteraz modelované kontaktné centrum pomocou Markovovského modelu M/M/m/∞, s počtom agentov m = 10. SHO 1 nech predstavuje IVR, reprezentované Markovovským modelom M/M/∞/∞.

6.1 Markovovský model M/M/∞/∞

Na rozdiel od modelu M/M/m/∞ tento model predpokladá nekonečne veľa obslužných staníc. Znamená to, že každá požiadavka, ktorá príde do systému je okamžite obsluhovaná, v tomto systéme neexistuje žiadny čakací rad, v systéme sa môže nachádzať nekonečne veľa požiadaviek naraz [3]. Je zrejmé, že takýto systém je vždy stabilný, t.j. nikdy nenastane situácia, že by bol systém zahltený množstvom požiadaviek, ktoré nedokáže obslúžiť. Priemerný počet požiadaviek v tomto systéme je (13):

(13)

Priemerný čas, ktorý strávi požiadavka v tomto systéme je (14):

(14)

6.2 Viacfázový SHO M/M/∞/∞ + M/M/m/∞

Nech prevádzkové parametre SHO 1 reprezentovaného modelom M/M/∞/∞ majú index 1 a prevádzkové parametre systému SHO 2 M/M/m/∞ majú index 2. Keďže jedným z predpokladov oboch týchto modelov je neobmedzená populácia požiadaviek, takýto viacfázový SHO sa nazýva otvorený. V otvorenom systéme platí [3]:

(15)

Celkový počet požiadaviek v systéme je (16):

(16)

Celkový čas, ktorý strávi požiadavka v systéme je (17):

(17)

6.3 Model kontaktného centra s IVR

Nech IVR v modelovanom kontaktnom centre reprezentuje model M/M/∞/∞ a samotné kontaktné centrum reprezentuje model M/M/m/∞ opísaný v predchádzajúcej časti práce. Priemerný čas obsluhy hovoru T_obs = 5 min nech je rozdelený nasledovne: požiadavka strávi v IVR priemerne T_obs1 = 1 min. Priemerný čas obsluhy hovoru agentom sa pomocou IVR skráti na T_obs2 = 4 min. Do kontaktného centra prichádza priemerne λ = 60 hovorov za hodinu. Samotný model systému je znázornený na obr. 8.

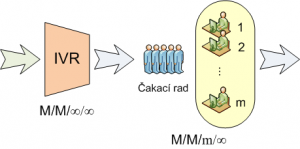
Obr. 8. Model kontaktného centra s IVR.

6.4 Vplyv IVR na modelované kontaktné centrum

Vplyv systému IVR na modelované kontaktné centrum je znázornený na obr. 9. Z priebehu závislostí stredného počtu požiadaviek v systéme od A [Erl] vidieť, že bod zlomu v systéme s IVR sa posunul až za hodnotu A = 11 Erl, na rozdiel od 9 Erl systému bez IVR. Systém s IVR je teda stabilný pri takom prevádzkovom zaťažení, kde model bez IVR už nie je možné použiť. Pomocou jednotky IVR je teda kontaktné centrum schopné pracovať pri prevádzkovom zaťažení do 11 Erl, čo predstavuje 132 prichádzajúcich hovorov za hodinu, pri priemernej dĺžke obsluhy hovoru 5 minút.

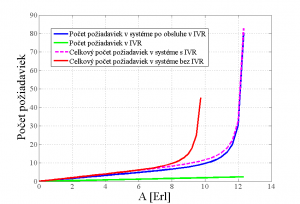
Obr. 9. Vplyv IVR na modelované kontaktné centrum.

Je zrejmé, že ak modelované kontaktné centrum bolo navrhnuté pre zvládnutie prevádzkového zaťaženia do 9 Erl, pričom bol potrebný počet agentov 10, po pridaní jednotky IVR do systému bude pri rovnakých podmienkach stačiť aj nižší počet agentov, čo predstavuje výrazné ušetrenie prevádzkových nákladov. Presné hodnoty sú uvedené v tab. 3.

Tab. 3 Porovnanie systémov s/bez IVR.

	A [Erl]	N1	N2	N	m	PQ [%]	Úspora [%]
bez IVR	5	−	−	5,04	10	3,61	−
s IVR	5	1,00	4,06	5,06	8	5,90	20
s IVR	5	1,00	4,02	5,02	9	2,38	10

Z tab. 3 vidieť, že pri A = 5 Erl sa v systéme s IVR a bez IVR priemerne nachádza takmer rovnaký počet požiadaviek. Rozdiel je ale v potrebnom počte agentov. Už pri 8 agentoch sa systém s IVR takmer vyrovná systému bez IVR, takýto systém ale ešte nespĺňa podmienku P_Q < 5 %. Systém s IVR pri počte agentov 9 dosahuje dokonca lepšiu hodnotu P_Q ako systém bez IVR s desiatimi agentmi. Jeden agent pri tomto systéme predstavuje 10 % z celkového počtu agentov. Použitie jednotky IVR teda prináša pomerne vysokú úsporu v potrebnom počte agentov. Túto skutočnosť vykresľuje parameter úspora v tab. 3.

7. Záver

Markovovský model M/M/m/∞ ponúka zaujímavý nástroj pre analýzu kontaktného centra. Najväčšou výhodou tohto modelu je, že ponúka veľmi široké spektrum výpočtov dôležitých prevádzkových parametrov kontaktného centra. Ďalšie možnosti prináša prepojenie modelu M/M/m/∞ s Erlangovým modelom C, najmä možnosť určenia GoS, ktorý môže byť jedným zo smerodajných parametrov pri posudzovaní QoS modelovaného kontaktného centra.

Nevýhodou tohto modelu sú naopak niektoré obmedzujúce základné predpoklady modelu, najmä predpoklady neobmedzenej populácie požiadaviek a nekonečnej kapacity čakacieho radu. Napriek tomu je možné tieto nevýhody obmedziť, napríklad pomocou zvolenej maximálnej hodnoty prevádzkového zaťaženia A, resp. pomocou parametra TW pri určovaní GoS. Zaujímavé výsledky prináša pridanie jednotky IVR do modelovaného kontaktného centra. Využitie problematiky viacfázového systému hromadnej obsluhy a prepojenie modelu M/M/m/∞ s modelom M/M/∞/∞ vytvára z Markovovského modelu M/M/m/∞ naozaj komplexný nástroj pre analýzu kontaktného centra.

8. Odkazy na literatúru

1. DIAGNOSTIC STRATEGIES: Traffic Modeling and Resource Allocation in Call Centers
   www.fer.hr/_download/repository/A4_1Traffic_Modeling.pdf
2. Bolch G., Greiner S., de Meer H., Trivedi K. S.: Queueing Networks and Markov Chains, vydal John Wiley & Sons, Inc., Hoboken, New Jersey, 2006
3. Polec J., Karlubíková T., Stochastické modely v telekomunikáciách 1, vydal Fond Jozefa Murgaša pre telekomunikácie n.f. vo vydavateľstve FABER, 1999, 1. vydanie, ISBN: 80-968125-0-5
4. Washington University in St. Louis, The Department of Computer Science & Engineering: Queuing theory
   http://www.cse.wustl.edu/~praveenk/support/quick-qt.pdf
5. Veeraraghavan M.: M/M/1 and M/M/m Queueing Systems, 20. Marec 2004
   http://www.ece.virginia.edu/mv/edu/715/lectures/QT.pdf
6. Hischinuma Ch., Kanakubo M., Goto T.: An Agent Scheduling Optimization for Call Cneter, In: The 2nd IEEE Asia-Pacific Services Computing Conference, 2007
7. Baroňák, I., Chromý, E.: Kontaktné centrum – súčasť modernej komunikačnej infraštruktúry, Telekomunikace, číslo 11, november, 2004, pp. 22-26
8. Wang J., Srinivasan R.: Staffing a Call Center with Interactive Voice Response Units and Impatient Calls, In: IEEE/SOLI 2008, IEEE International Conference, 2008

---

Spoluautorom článku je Ing. Erik Chromý, PhD. , Katedra Telekomunikácií, Fakulta elektrotechniky a informatiky, Slovenská technická univerzita, 812 19 Bratislava, Slovenská republika

---

Práca bola prezentovaná na Študentskej vedeckej a odbornej činnosti (ŠVOČ 2011) v sekcii Telekomunikácie a získala Cenu dekana, ISBN 978-80-227-3508-7