Pro řízení systémů, resp. technologických procesů, je v dnešní době samozřejmý požadavek na co nejefektivnější a nejrychlejší běh algoritmů řízení. Pro diskrétní řízení je tato skutečnost nutností pokud uvažujeme velmi malé periody vzorkování. V předkládaném článku je analyzována práce algoritmu GPC prediktivního řízení z hlediska jeho výpočetní rychlosti, a to zejména z pohledu závislosti na různé volbě typu matematického popisu modelu, který tvoří jednu z podstatných komponent GPC regulátoru.

Podle odborných pramenů je typ matematického popisu řízeného systému libovolně zaměnitelný. Různě popsané modely systémů uvnitř regulátoru dají apriorně totožné výsledky. Mají ale odlišně složité odvození a vyčíslení svých numerických záležitostí v každé periodě vzorkování. Pokud by se v článku ukázalo, že popisovat systémy vnějším popisem (přenosovou funkcí nebo přenosovou maticí) je výhodnější oproti stavovému popisu nebo naopak, může tato volba opět o něco urychlit výpočty, sice v malém měřítku, ale i tak je každá úspora výpočetního času důležitá. Popisy lze podle potřeby mezi sebou vzájemně převádět (vnější na stavový a naopak). To, zda-li má volba typu modelu řízeného systému na rychlost výpočtů alespoň nějaký vliv, je zkoumáno dále v uvedené práci i s diskuzí výsledků měření v závěru.

Pojednání o GPC prediktivním řízení

Prediktivní řízení, dále s uvažovanou variantou GPC (Generalized Predictive Control), patří obecně mezi metody řízení. Prakticky je zejména realizováno v diskrétní oblasti. Jeho algoritmy jsou mnohostranně použitelné, a to pro různé charaktery řízených objektů. Lze jimi ovládat například i neminimálně fázové a nestabilní procesy a dále též i varianty s dopravním zpožděním. Metoda prediktivního návrhu je vhodná pro jednorozměrné i vícerozměrné systémy. V odborné literatuře se vyskytují srovnání s jinými způsoby řízení hovořící častokrát ve prospěch prediktivního přístupu. Předností prediktivního řízení je možnost zakomponovat požadavek na omezení rozsahů veličin a jejich změn již při samotném návrhu algoritmu. Je možné takto omezovat řídicí, stavové a regulované veličiny resp. signály. [1][2]

Z pohledu struktury zahrnuje prediktivní regulátor dvě důležité komponenty, kterými jsou matematický model řízeného systému a optimalizátor. Obě tyto součásti jsou pro odvození vztahů algoritmu řízení stejně významné. Integrace modelu do regulátoru je právě pro GPC řízení charakteristické. Umožňuje definovat model systému různými ekvivalentními způsoby. Typy popisu korespondují s jejich kategorizací v rámci teorie systémů a jsou buď vnitřní (stavové) nebo vnější (přenosová funkce, přenosová matice a další).

Optimalizátorem řešíme výpočet výsledného řídicího signálu. Pro případ nezahrnutých omezení veličin se jedná o úlohu volného vícerozměrného extrému. Výpočetní vztah je potřeba pro algoritmus vyjádřit analyticky ve formě maticové rovnice. Při existenci požadavků na omezení vyvstává požadavek řešit úlohu neklasicky vázaného extrému. Řešení optimalizační části je v podstatě modul, který již nespadá přímo pod prediktivní řízení, ale je jím pouze využíván. Můžeme jej tedy numericky implementovat dle postupů řešení optimalizačních metod z literatury nebo využít hotová řešení specializovaných výpočetních nástrojů např. MATLAB. [1][2][3][4]

Výše popsaná struktura regulátoru je nastavitelná parametricky v souvislosti se samotnou podstavou a filozofií prediktivního řízení. Jedná se o myšlenku pohyblivého horizontu, kdy jsou vzhledem ke stávajícímu okamžiku řízení stanoveny predikce průběhů veličin, a to na základě znalosti dosavadních informací. Velikostí horizontu lze ovlivňovat kvalitu regulace. Horizont se dělí na minimální, maximální a řídicí. Poslední je zaveden pro redukci výpočetní složitosti.

Za vstupní informace pro výpočet lze považovat průběh žádané veličiny, minulé hodnoty přírůstků akčních zásahů, minulé hodnoty stavů a regulované veličiny. Další skutečnosti ovlivňující řízení jsou matematického charakteru, a to ve smyslu výběru tvaru účelové funkce, stanovení jejích váhových koeficientů. Důležité je si uvědomit, že predikované veličiny mají platnost pouze pro aktuální okamžik vzorkování a poté musí být jejich výpočet opakován. Celkové schéma GPC řízení je znázorněno na sjednocujícím schématu (Obr.1), kde je uvažována varianta pro vnější i vnitřní popis modelu systému uvnitř regulátoru. [1][2][3]

Obr.1 Schéma GPC řízení s modelem systému popsaného ve vnitřní nebo vnější oblasti

Vybrané typy popisů a jejich možný vliv na řízení

Pro studium vlivů použitého typu popisu řízeného systému byly vybrány oblasti vnější a vnitřní stavová. Pro zvýšení variability při zkoumaní aspektů jsou navíc tyto typy rozčleněny na případ jednorozměrné a vícerozměrné varianty řízeného objektu. Před zahájením měření je uvažováno, že mohou mít typy modelů vliv na práci se samotným zpracováním matematického popisu (vnější popis – zpracování pouze koeficientů polynomů, vnitřní – práce s maticemi), analytickým určením predikčních rovnic při návrhu algoritmu (vnitřní popis má menší výpočty a pro různé rozměry procesů podobnou strukturu rovnic, vnější popis má odvozování složitější) a dále numerické výpočty nad modely, které jsou integrovány přímo do výpočetních vztahů řízení.

Ověření vlivu typu popisů v simulaci GPC řízení v programu MATLAB

Byly navrženy algoritmy GPC prediktivního řízení v prostředí MATLAB, a to v podobě M souborů. V kódu byly zahrnuty měřicí funkce pro zjištění výpočetního času a tyto výsledky byly statisticky zprůměrňovány v rámci své kategorie. Pro měření byly použity matematicky vyjádřené simulační modely. Jednorozměrný systém je popsán přenosovou funkcí (1) a jí ekvivalentním stavovým popisem (2), mnohorozměrný systém je vyjádřen přenosovou maticí (3) a jí ekvivalentním vnitřním popisem (4).

Stěžejní je poté porovnání jednotlivých časů pro dvojice (1) – (2) a (3) – (4), z čehož případně vyplyne výhoda některého z typů popisů nebo se naopak ukáže jejich shodná použitelnost. Výsledky zprůměrovaných měření po sérii deseti dílčích měření pro dvojice ekvivalentních popisů jsou uvedeny v tabulce (Tab.1). Na obrázcích (Obr.2), (Obr.3) je zdokumentována ekvivalentnost různých popisů téhož systému bez dopadu na správnost výsledků při provedené simulaci GPC v prostředí MATLAB.

(1)

(2)

(3)

(4)

Tab.1 Výsledky měření běhu GPC algoritmu s různými typy popisu modelu uvnitř regulátoru

	V řádku tabulky jsou ekvivalentní zaměnitelné popisy modelu
Rozměr systému	Typ popisu (rovnice popisu)	Průměrná doba běhu GPC [s]	Typ popisu (rovnice popisu)	Průměrná doba běhu GPC [s]
jednorozměrný	vnější (1)	0,4953 [s]	vnitřní-stavový (2)	0,67 [s]
vícerozměrný	vnější (3)	0,5079 [s]	vnitřní-stavový (4)	0,8139 [s]

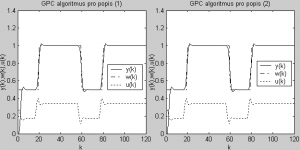
Obr.2 Zaměnitelnost popisů systému (1) a (2) bez vlivu na správnost výsledků v MATLABu

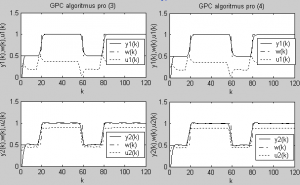
Obr.3 Ekvivalence popisů systému (3) a (4) s korektně shodnými výsledky v MATLABu

Závěr

V předkládaném článku byla podrobněji prozkoumána oblast možnosti ekvivalentního popisu modelu řízeného systému v GPC prediktivním řízení, v jehož algoritmu je tento model zahrnut. V práci byl zkoumán právě vliv volby typu modelu na výpočetní čas celého algoritmu GPC prediktivního řízení, a to při simulaci ve vytvořeném programovém řešení v podobě M souborů v prostředí MATLAB. Při různě matematicky definovaném totožném systému vychází všechny průběhy veličin stejně (Obr.2, Obr.3). Ale po výpočetní stránce se na základě provedené série měření výpočetního času běhu algoritmu ukázalo, že je lepší volit vnější popis systému. Vnější popis systému má rychlejší časy běhu algoritmu než-li vnitřní stavový popis.

Rozdíly mezi aplikovanými typy popisů sice vycházely v řádech desetin sekundy, ale i přesto jsou rozdíly významné při diskrétním řízení v dnešní době. Stavové výpočty může zpomalovat práce s maticemi, kdežto u vnějšího popisu pracujeme pouze s koeficienty polynomů. Aby zde nebylo vnitřnímu popisu křivděno, je nutné podotknout i výhody stavového popisu, kterými jsou lepší odvození prediktivních rovnic při analytickém návrhu algoritmu GPC. Tyto rovnice mají podobný tvar jak pro jednorozměrné tak pro vícerozměrné systémy, a to ne s tolika odlišnostmi jako je tomu u složitějších rovnic predikcí vnějšího popisu.

Poděkování

Článek byl uskutečněn za finanční podpory IGA Univerzity Tomáše Bati ve Zlíně, Fakulty aplikované informatiky číslo IGA/FAI/2012004.

Použitá odborná literatura

1. BOBÁL, Vladimír. Adaptivní a prediktivní řízení. 1. vyd. Zlín: Univerzita Tomáše Bati, Fakulta aplikované informatiky, 2008. 134 s. ISBN 978-80-7318-622-3.
2. WANG, Liuping. Model Predictive Control System Design and Implementation Using MATLAB. 1. vyd. London: Springer-Verlag Limited, 2009. 366 s. ISBN 978-1-84882-330-3.
3. CORRIOU, Jean-Pierre. Process control: theory and applications. 1. vyd. London: Springer, 2004. 752 s. ISBN 1-85233-776-1.
4. KUBALČÍK, M., BOBÁL, V. Computation of predictions in multivariable predictive control, Proceeding ACMOS’11 Proceedings of the 13th WSEAS international conference on Automatic control, modelling & simulation, 2011. ISBN 978-1-61804-004-6.

---

Spoluautorom článku je M. Kubalčík, Univerzita Tomáše Bati, Fakulta aplikované informatiky, Ústav řízení procesů, nám. T. G. Masaryka 5555, 760 01 Zlín, ČR