Pri praktickom určovaní odporu riečnych lodi sa dnes používajú výsledky modelových skúšok a štatistické metódy, čo sú zovšeobecnené empirické vzťahy založené na výsledkoch systematicky robených modelových skúšok, platné vždy pre určitý typ a parametre plavidla. V poslednom čase do tejto oblasti, podobne ako do iných technických odborov, preniká numerické modelovanie prúdenia, známe pod označením CFD (Computational Fluid Dynamics).

V porovnaní s experimentom sú počítačové simulácie menej nákladné po stránke času aj financií. Štatistické metódy sú oproti tomu pomerne rýchle na výpočet, ale v súčasnosti sa dajú spoľahlivo použiť najmä v oblasti námorných lodí. V prípade riečnych plavidiel aj s uvážením obmedzenej hĺbky sú pomerne nepresné a s veľkým rozptylom výsledkov jednotlivých metód, ktoré svojim rozsahom platnosti vyhovujú danému plavidlu.

Nevýhodou CFD simulácií v súčasnosti je rôznorodosť metód a matematických modelov popisujúcich turbulentné prúdenie. Preto sa robí v danom odbore množstvo porovnávacích štúdií s výsledkami experimentu s cieľom zistiť najvhodnejšie nastavenie matematického modelu za účelom získania spoľahlivých výsledkov a zistenia ich odchýlok od výsledkov experimentu. Len v prípadoch korektných výsledkov pri veľkom množstve porovnávacích analýz sa dá výsledkom CFD simulácií naplno dôverovať a nahrádzať nimi nákladný experiment v danej oblasti.

1. Popis riešeného problému

Tento príspevok je venovaný porovnávacej štúdii výsledkov CFD simulácie, experimentu a výsledkov štatistických metód práve v oblasti riečnych lodí v obmedzených hĺbkach. Obmedzené hĺbky spôsobujú zmenu rýchlostí a tlakov okolo trupu lode, čím zásadne ovplyvňujú celkový odpor plavidla aj všetky jeho jednotlivé zložky, ale vedú aj ku zmene jeho ponoru, prípadne aj pozdĺžneho sklonu. Podiel vplyvu obmedzenej hĺbky na tieto veličiny je závislý od:

• pomernej hĺbky plavebnej dráhy h/T, kde h je hĺbka plavebnej dráhy a T ponor lodi
• kritéria dynamickej podobnosti pre obmedzené hĺbky vo forme Froudeho hĺbkového čísla, definovaného vzťahom (1)

(1)

Z Froudeho hĺbkového čísla sa dá potom vyjadriť kritická rýchlosť pre výtlačný režim plavby v obmedzenej hĺbke. Pri tejto rýchlosti je Fr_h = 1

(2)

Porovnanie celkového odporu a zanorenia vplyvom obtekania trupu v obmedzenej hĺbke je ukázané na trupe riečnej osobnej lode Kyjev (ďalej značené OL Kyjev) s ponorom T = 2m a hĺbku plavebnej dráhy h = 2,5m. OL Kyjev predstavuje plavidlo plynulejšich tvarov, s tunelovou kormou pre umiestnenie dvoch vrtúľ. Numerická simulácia bola vytvorená s použitím všeobecného komerčného softvéru Ansys Fluent 13.0, ktorý je založený na riešení diskretizovaných Navier-Stokesových rovníc metódou konečných objemov.

Výsledky experimentu boli prebrané z výskumnej správy Ukrajinskej Akadémie vied v Kyjeve, pre výpočet celkového odporu a zanorenia štatistickými metódami bol využitý program RAFTER vytvorený na OALSM SjF STU v Bratislave doc. Ing. Petrom Patekom, CSc. Parametrom (pomerové číslá a súčinitele plnosti) a typu daného plavidla svojim rozsahom platnosti vyhovujú štyri štatistické metódy, menovite podľa Karpova, Zvonkova, Pavlenka a Qiana. Trup OL Kyjev má následujúce základne parametre:

Dĺžka maximálna	Lmax = 127,72 m
Dĺžka na vodoryske pri T=2m	LWL = 122,75 m
Šírka na vodoryske pri T=2m	BWL = 16,2 m
Ponor	T = 2 m
Výška boku	H = 3,8 m
Objemový výtlak pri T=2m	Δ = 3297 m3
Omočený povrch trupu pri T=2m	SW = 2175 m2
Plocha vodorysky pri T=2m	AWL = 2175 m2

2. Príprava numerickej simulácie

Prvým krokom pri numerickom modelovaní je tvorba geometrického modelu. 3D model trupu OL Kyjev, resp. jeho jedna polovica z dôvodu symetrie trupu aj prúdenia okolo osovej roviny, je vytvorený v programe Catia v5r18 na základe teoretického výkresu, viď obr. 1. Tento model je následne importovaný do programu Ansys Workbench, preprocesora CFD programu Fluent. Tu nasledovalo vytvorenie objemu okolitého prostredia kvádrového tvaru tak, aby osová rovina prostredia bola totožná s osovou rovinou trupu.

Následne je objem trupu boolovskou operáciou odčítaný od objemu práve vytvoreného prostredia. Geometrickým modelom je striktne určený pomer hĺbky plavebnej dráhy ku ponoru plavidla. Vzdialenosť dna tekutej oblasti a dna plavidlá je teda totožná s maržou v reálnych podmienkach. Čiže pre každú pomernú hĺbku je potrebné modifikovať geometrický model.

Obr. 1: Teoretický výkres OL Kyjev

Ďalším krokom je prevedenie vytvoreného geometrického modelu do mierky. Počítačové simulácie sú zvyčajne podobne ako modelové skúšky robené v mierke z dôvodu ich riešiteľnosti dostupnou výpočtovou technikou. Bola použitá rovnaká mierka ako pri modelovej skúške 1 : 25 na základe ktorej bude neskôr vykonaný prepočet vypočítaných hodnôt na skutočné plavidlo pomocou Froudeho metódy.

Teraz je geometria kompletná, nasleduje diskretizácia výpočtovej oblasti, čiže tvorba siete rozdeľujúcej geometriu na konečne objemy. Zvolená bola hybridná sieť s neštruktúrovanými bunkami v blízkosti lodného trupu a štruktúrovanými v oblasti vzdialenejšej, viď obrázok č. 2. Táto sieť je optimálnejšia z pohľadu počtu buniek a ich kvality v porovnaní s prípadom použitia neštruktúrovanej siete v celom objeme, čo následne pozitívne ovplyvňuje čas trvania výpočtu. Pre výpočet je v prípade lodi potrebná jemná sieť na povrchu lodného trupu v oblasti medznej vrstvy, ale tiež v blízkosti voľnej hladiny z dôvodu ostrosti modelovaného prechodu jednotlivých tekutín – vody a vzduchu.

Pre uľahčenie diskretizácie boli vytvorené pomocné rezy oddeľujúce jednotlivé typy sietí a tiež umožňujúce lokálne zhustenie siete práve v úrovni vodnej hladiny. Na samotný výpočet prúdenia a zvlnenej vodnej hladiny počas neho tieto rezy nemajú žiadny vplyv. Z dôvodu obmedzeného času pre tvorbu simulácie bola zvolená pomerne hrubá sieť, obsahujúca približne 1∙10⁶ buniek, ale pre výpočet najpodstatnejšej veličiny z hľadiska návrhu pohonnej jednotky plavidla – celkového odporu, postačujúca.

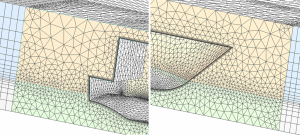
Obr. 2: Ukážka výpočtovej siete OL Kyjev v oblasti čela (vpravo) a kormy

Týmito krokmi bol vytvorený kompletný geometrický model, nasleduje nastavenie matematického modelu v programe Fluent. Sú uvažované predpoklady totožne s podmienkami modelovej skúšky v skúšobnom bazéne:

• lineárny ustálený pohyb plavidla s konštantnou rýchlosťou
• vodná hladina bez vĺn a vplyvu riečneho prúdu
• ploché dno plavebnej dráhy bez prírodných nerovností

Aplikované okrajové podmienky sú definované nasledujúcou tabuľkou č. 1 a ukázané na obrázku č. 3 :

Tab. 1: Definícia okrajových podmienok

Plocha	Okrajová podmienka	Popis
Vstup vody/vzduchu	Pressure-inlet	Definuje rýchlosť plavidla, smer prúdenia, otvorený kanál, úroveň hladiny a dna plavebnej dráhy
Výstup vody/vzduchu	Pressure-outlet	Definuje smer prúdenia, otvorený kanál, úroveň hladiny a dna plavebnej dráhy
Trup	Wall	Stacionárna stena, definuje drsnosť povrchu ak je uvažovaná
Dno plavebnej dráhy	Wall	Pohybujúca sa stena o rýchlosti plavidla, definuje drsnosť povrchu ak je uvažovaná
Vzdialený okraj	Wall	Stacionárna stena s nulovým trením
Rovina symetrie	Symmetry	Definuje rovinu symetrie pre symetrické prúdenia

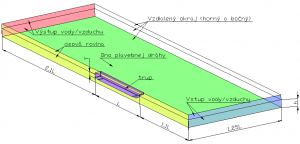
Obr. 3: Definícia okrajových podmienok

Ostatné nastavenia matematického modelu udáva tabuľka č. 2:

Tab. 2: Základne nastavenia matematického modelu

Riešič	Pressure based, steady
Model	Multiphase, volume of fluid
Parametre objemového zlomku	Open channel flow – implicit
Model turbulencie	Realizable k – ε, standard wall functions
Interpolačné schémy	Tlak – presto, Moment – second order upwind, Objemový zlomok – modified HRIC, k, ε – second order upwind

3. Výpočet a vyhodnotenie numerickej simulácie

Časovo nezávislé simulácie sú spravené pre rýchlosti uvedené v tabuľke č. 3 spoločne s výsledkami modelovej skúšky pre celkový odpor a zanorenie. Pre matematické vyjadrenie turbulentného prúdenia je využitá metóda Reynoldsoveho spriemerovania Navier-Stokesových rovníc, tzv. RANSE (Reynolds Averaged Navier-Stokes Equations), konkrétne je na základe predchádzajúcich skúseností pre danú problematiku zvolený model realizable k – ε. Pre docielenie konvergencie bolo potrebných cca 15 000 iterácií.

Tab. 3: Výsledky modelovej skúšky pre T=2m a h=2,5m

v [km/h]	v [m/s]	Frh [ – ]	RT [kN]	ΔT [cm]
8	2,22	0,449	34,09	7,25
8,5	2,36	0,477	47,66	9,75
9	2,50	0,505	62,37	13,75
9,4	2,61	0,527	82,81	17,25

Hodnoty odporu sú priamo odčítané ako sila na trupe v smere osi x a prepočítané už spomínanou Froudeho metódou na skutočné plavidlo. Zanorenie vplyvom obmedzenej hĺbky sa určí z vertikálnej sily na trupe, na základe zákona geometrickej podobnosti prenásobením modelovej hodnoty treťou mocninou mierky dĺžok λ, ktorá má hodnotu 25, sa prepočíta na skutočné plavidlo. Zanorenie je potom ekvivalentné rozdielu tejto vertikálnej sily a sily vztlakovej, vyjadrený hodnotou ΔV a o ktorý by bolo potrebné zvýšiť výtlak, aby bol splnený Archimedov zákon. Výsledky z tohto výpočtu s absolútnou a relatívnou odchýlkou od experimentu udáva tabuľka 4. Tie sú určené podľa

Absolútna odchýlka = výpočet – experiment [kN, cm]

(3)

Relatívna odchýlka = (výpočet – experiment)/(experiment) . 100[%]

(4)

Tab. 4: Výpočet odporu a zanorenia numerickým modelovaním s odchýlkami výsledkov od experimentu

v [km/h]	Modelové hodnoty			Skutočné hodnoty			Odchýlka od experimentu
	v [m/s]	RTm [N]	FZ [N]	RT [kN]	ΔV [m3]	ΔT [cm]	ΔRT [kN]	ΔRT [%]	Δ(ΔT) [cm]	Δ(ΔT) [%]
8	0,444	2,96	1913,1	34,02	249,9	13,3	-0,07	-0,20	6,1	83,82
8,5	0,472	3,65	1887,7	43,44	291,9	15,6	-4,22	-8,86	5,8	59,69
9	0,500	4,62	1875,4	57,17	309,9	16,5	-5,20	-8,34	2,8	20,22
9,4	0,522	6,18	1856,0	80,36	340,8	18,2	-2,45	-2,96	0,9	5,38

Pretože ide o časovo nezávislú simuláciu, kde lodný trup má v geometrickom modeli fixnú polohu, ktorá neumožní uvažovať zanorenie počas priebehu simulácie, je treba manuálne vytvoriť korekciu pre výpočet celkového odporu, ktorá s týmto zanorením uvažuje. Keďže aj veľkosť samotného zanorenia je ovplyvnená fixným modelom a s uvážením rovnice kontinuity a Bernoulliho rovnice sa dá predpokladať, že je menšia, je nevyhnutné doplniť prídavok na zanorenie ku hodnote vypočítanej v prvej simulácii. Pre určenie veľkosti prídavku bol využitý samotný podiel zmeny výtlaku ΔV ku výtlaku plavidla V a bol aproximovaný podľa vzťahu 5. Po štvrtej aproximácii už bolo navýšenie aj pri najvyšších rýchlostiach zanedbateľné.

(5)

Výsledné zanorenie pôsobením obmedzenej hĺbky je potom uvedené v tab. 5. Pre tieto hodnoty sú upravené geometrické modeli pre jednotlivé rýchlosti, kde trup je v geometrickom modeli posunutý o hodnotu výsledného zanorenia, samozrejme prepočítanú do modelových hodnôt pomocou mierky dĺžok λ.

Tab. 5: Aproximácia prídavku k rozdielu výtlaku, výsledné zanorenie

v [km/h]	ΔV [m3]	ΔT [cm]	Odchýlka od experimentu
			Δ(ΔT) [cm]	Δ(ΔT) [%]
8	270,4	14,4	7,2	98,90
8,5	320,3	17,1	7,3	75,20
9	342,1	18,2	4,5	32,69
9,4	380,1	20,3	3,0	17,53

Korigované výsledné hodnoty celkového odporu s odchýlkami od experimentu a kontrola rozdielov vztlakovej a vertikálnej sily je uvedená v tab. 6. Tento rozdiel by mal byť nulový, resp. blízky nule. Rozdiel v tomto prípade ešte existuje, ale vzhľadom k tomu, že by spôsobil zvýšenie ponoru o 1 až 2 cm bol zanedbaný. V prípade špeciálnych požiadavkov na presnosť by sa vytvorila druhá korekcia a vykonal ďalší numerický výpočet s týmto zvýšeným ponorom.

Tab. 6: Korigovaný výpočet odporu a zanorenia numerickým modelovaním s odchýlkami výsledkov od experimentu

v [km/h]	Modelové hodnoty			Skutočné hodnoty		Odchýlka od experimentu
	v [m/s]	RTm [N]	FZ [N]	RT [kN]	ΔV [m3]	ΔRT [kN]	ΔRT [%]
8	0,444	3,05	2048,6	35,43	34,1	1,34	3,92
8,5	0,472	3,91	2045,1	47,50	39,6	-0,16	-0,33
9	0,500	5,12	2052,8	64,98	27,4	2,61	4,19
9,4	0,522	6,54	2039,9	85,99	47,9	3,17	3,83

Výsledky jednotlivých štatistických metód pre celkový odpor a zanorenie sú uvedené v tab. 7, ich odchýlky od experimentu potom v tab. 8. Grafické porovnanie výsledkov celkového odporu experimentu (čierna krivka), prvej aj korigovanej CFD simulácie a výsledky štatistických metód (čiarkované krivky) zobrazuje obr. 4. Výsledky pre zanorenie vplyvom plavby v obmedzenej hĺbke potom zobrazuje graf na obr. 5.

Tab. 7: Výpočet odporu a zanorenia štatistickými metódami

v [km/h]	Zanorenie	Karpov	Zvonkov	Pavlenko	Qian
	ΔT [cm]	RT [kN]	RT [kN]	RT [kN]	RT [kN]
8	9,3	19,4	17,5	41,1	14,1
8,5	10,5	22,4	20,5	46,6	15,8
9	11,8	25,9	23,9	52,6	18,0
9,4	12,8	28,9	27	57,8	21,5

Tab. 8: Odchýlky výsledkov štatistických metód od experimentu

v [km/h]	Zanorenie		Karpov		Zvonkov		Pavlenko		Qian
	Δ(ΔT) [cm]	Δ(ΔT) [%]	ΔRT [kN]	ΔRT [%]	ΔRT [kN]	ΔRT [%]	ΔRT [kN]	ΔRT [%]	ΔRT [kN]	ΔRT [%]
8	2,05	28,28	-14,69	-43,09	-16,59	-48,67	7,01	20,56	-19,99	-58,64
8,5	0,75	7,69	-25,26	-53,00	-27,16	-56,99	-1,06	-2,22	-31,86	-66,85
9	-1,95	-14,18	-36,47	-58,47	-38,47	-61,68	-9,77	-15,67	-44,37	-71,14
9,4	-4,45	-25,80	-53,91	-65,10	-55,81	-67,40	-25,01	-30,21	-61,31	-74,04

Obr. 4: Grafické porovnanie výsledkov pre celkový odpor

Celkový odpor podľa numerickej simulácie v tomto prípade pomerne presne kopíruje krivku nameraných hodnôt. Korekcia odchýlky celkového odporu od nameraných hodnôt mierne zmenšila. Oproti tomu štatistické metódy platné pre daný prípad vykazujú veľký rozdiel a rozptyl vo výsledkoch. Najbližšie výsledkom modelovej skúšky sa nachádza metóda podľa Pavlenka, ostatné vykazujú oproti experimentu výrazne nižšie hodnoty. V prípade zanorenia sú výsledné hodnoty CFD simulácie väčšie ako namerané, štatistická metóda vykazuje menší rozdiel.

Obr. 5: Grafické porovnanie výsledkov pre zanorenie

4. Záver

Tento príspevok prináša stručný návod pre tvorbu časovo nezávislej CFD simulácie s použitím RANSE metód, ich aplikáciu na problematiku plavby riečnych lodí v obmedzených hĺbkach a tvorbu korekcií uvažujúcich vplyv zanorenia na odpor lodi. Simulácie boli spravené pre niekoľko pomerných hĺbok. Z dôvodu rozsiahlosti nebolo možné v príspevku uviesť výsledky pre všetky prípady, preto bol na ukážku vybratý iba jeden.

Z tejto porovnávacej analýzy vidieť, že numerické modelovanie je v prípade celkového odporu použiteľné pre jeho určovanie v praxi, alebo aspoň pri rýchlostiach zaujímavých pre návrh propulzie. V porovnaní s bežne používanými štatistickými metódami vykazuje menšie odchýlky od skutočnosti. V prípade zanorenia CFD simulácia udáva väčšie hodnoty pri nízkych rýchlostiach, pri vyšších sa zvyčajne približuje ku hodnotám modelovej skúšky.. Táto veličina má význam najmä pri malých pomeroch h/T, z hľadiska bezpečnosti a zabránení kolízie trupu s dnom plavebnej dráhy. Keďže pri CFD vykazuje všeobecne väčšie hodnoty, predstavuje akúsi mieru bezpečnosti. Bežne ale riečne lode vo výtlačnom režime pri vysokých rýchlostiach okolo F_rh = 0,8 neplávajú, z dôvodu ekonomiky prevádzky aj poškodzovania brehov vlnami.

Tvorba porovnávacích analýz je dôležitá pre overenie validity výsledkov CFD simulácií a z dôvodu nájdenia vhodného nastavenia matematického modelu pre danú oblasť použitia. Len tak možno numerické modelovanie spoľahlivo použiť pri riešení praktickej úlohy návrhu alebo optimalizácie.

Poďakovanie

Táto štúdia vznikla s podporou Centre of Excellence for New Technologies in Electrical Engineering – CENTE II, ITMS code 26240120019, supported by the Research and Development Operational Programme funded by the ERDF.

Použitá literatúra

1. Akademija nauk Ukrajiny, Institut hydromechaniky (1992): Výsledky modelovej škúšky osobnej lode Kyjev, Kyjev
2. Ansys, Inc (): ANSYS FLUENT 13.0 Documentation
3. Beneš, P. – Kollárik, R.: (2011): Preliminary computational fluid dynamics (CFD) simulation of EIIB push barge in shallow water, ISSN: 1338-1954, ONDÁR, E. — ČEKAN, M. — HORVÁT, M. Vol. 19/2011, Bratislava
4. Kozubková, M. (2008): Modelování proudění tekutin – FLUENT, CFX, VŠB – TU Ostrava, Ostrava, 153
5. SLK (1992): Výkresová dokumentácia OL Kyjev – výkresy č. 92-12/273-001-001 (1, 4, 5), Komárno
6. Tichý, J.- Patek, P. (2006): Teória lode, ISBN: 80-227-2466-1, Vydavateľstvo STU, Bratislava, 355 s