Výpočet hraničnej plochy použitím PC
24. September, 2012, Autor článku: Guzan Milan, Elektrotechnika
Ročník 5, číslo 9  Pridať príspevok
Pridať príspevok
![]() Príspevok pojednáva o súčasných možnostiach výpočtu hraničných plôch (HP), ktoré majú využitie v takých elektronických obvodoch ako sú sekvenčné a chaos generujúce obvody. Zároveň je však venovaný priestor aj histórii výpočtov HP v časoch, keď ešte neboli osobné počítače (PC) k dispozícii resp. mali malý výkon – avšak na vtedajšie výpočty plne postačovali. Výkony jednotlivých procesorov (CPU) sú zhrnuté v tabuľkách i grafoch. Tie naznačujú, že aj keď dnešné procesory nemajú príliš vysoký hodinový kmitočet v porovnaní s predchádzajúcimi CPU, ich výkon je vyšší.
Príspevok pojednáva o súčasných možnostiach výpočtu hraničných plôch (HP), ktoré majú využitie v takých elektronických obvodoch ako sú sekvenčné a chaos generujúce obvody. Zároveň je však venovaný priestor aj histórii výpočtov HP v časoch, keď ešte neboli osobné počítače (PC) k dispozícii resp. mali malý výkon – avšak na vtedajšie výpočty plne postačovali. Výkony jednotlivých procesorov (CPU) sú zhrnuté v tabuľkách i grafoch. Tie naznačujú, že aj keď dnešné procesory nemajú príliš vysoký hodinový kmitočet v porovnaní s predchádzajúcimi CPU, ich výkon je vyšší.
Úvod
Význam hraničnej plochy (HP) u sekvenčných a chaos generujúcich obvodov je obrovský. Pre ilustráciu uvedieme niekoľko príkladov. Skutočnosť, že sa polovodičová pamäť po pripojení na napätie sa dostane vždy do toho istého logického stavu, súvisí s prítomnosťou HP a nasledným rozdelením stavového priestoru na regióny príťažlivosti zodpovedajúce jednotlivým logickým úrovniam [1]. Poznanie morfológie HP umožňuje už pri návrhu novej binárnej, či viac-hodnotovej perspektívnej pamäte, rozhodnúť o vhodnosti navrhnutých parametrov prvkov.
Tiež nie je zanedbateľná možnosť štúdie vplyvu parazitných akumulačných prvkov na čipe nielen na dynamiku obvodu, ale vôbec na schopnosť správne pracovať. Pod pojmom „schopnosť správne pracovať“, sa v prípade pamätí rozumie bezproblémový zápis či prepis jej informačného obsahu, čo pri nevhodnej morfológii HP spôsobí jej afunkčnosť [2]. Akékoľvek snahy obíjsť výpočet a zobrazenie HP znamenajú vpodstate, pri vývoji nových pamätí, používanie metódy „pokus-omyl“ čo je veľmi zdĺhavé a neefektívne.
V prípade chaos generujúcich obvodov tkvie význam HP v tom, že umožní pochopenie dejov prebiehajúcich v analyzovanom obvode [3], ktorého výstupný signál nie je možné predikovať. Navyše, ak by bol takýto signál využitý na utajený prenos signálu, tak modulačný signál nesmie prekročiť HP. Ak sa to stane, potom nepredikovateľný chaotický signál vystrieda ľahko predikovateľný periodický signál. Získanie utajenej správy by potom pre tretiu stranu nebol problém.
Na výpočet HP je však potrebný istý výpočtový výkon. S nástupom výkonnejších CPU a rastúcimi možnosťami vizualizácie HP nielen 2D rezmi, ale priamo v 3D, vzniká otázka efektivity výpočtu väčšieho množstva 2D rezov pre potreby rekonštrukcie HP v 3D stavovom priestore [4], [5]. Pretože autor príspevku sa touto problematikou zaoberá už 20 rokov, zhŕňa možnosti CPU používaných v minulosti a porovnáva so súčasnými možnosťami, ktoré ponúkajú dnešné, či nedávno minulé CPU.
Možnosti výpočtu HP
Finálnemu zobrazeniu HP napr. v 3D, ktoré ilustruje obr. 1, predchádza výpočet trajektórií, ktorých začiatočné podmienky sú nositeľkami informácie o regiónoch príťažlivosti pre jednotlivé atraktory. Zobrazenie HP bude závisieť od rozmeru stavového priestoru.
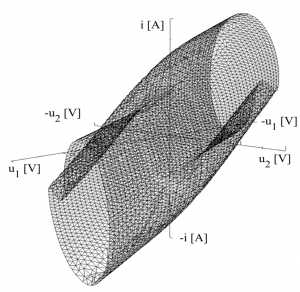
(a)
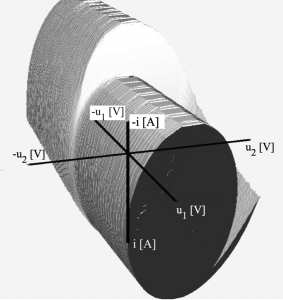
(b)
Obr. 1 Príklady vizualizovanej 3D HP Chuaovho obvodu pre rôzne parametre a vizualizačné techniky
Čím bude m menšie (minimálne však m = 2), tým bude výpočet HP i technika jej zobrazenia menej náročná nielen na samotnú vizualizáciu, ale i na predstavivosť čitateľa pri umiestnení HP v priestore resp. v rovine. Prvé práce, ktoré názorne ilustrovali výpočet trajektórií a rozdelenie stavového priestoru (stavovej roviny pri m = 2) na jednotlivé atrakčné oblasti, boli prezentované v 60. rokoch minulého storočia, kedy výpočtová technika nebola bežne dostupná. Autor týchto prác zovšeobecnil už známe resp. vypracoval nové grafické metódy konštrukcie trajektórií nielen v rovine [6], [7], ale aj v priestore, kde m ≥ 3 [8] – [11].
Pri riešení diferenciálnych rovníc grafickými metódami bola konštatovaná dostatočná presnosť, ba dokonca ručná grafická konštrukcia trajektórie bola rýchlejšia ako jej samotný numerický výpočet [12]. Správnosť naznačených trajektórií uvedených v práci [13] bola pozitívne komentovaná austrálskym autorom práce [14] a potvrdená výpočtom trajektórií analógovým počítačom. Lenže pri požiadavke výpočtu a zobrazenia väčšieho počtu trajektórií sa stalo ich zostrojovanie grafickými metódami z časového hľadiska neúnosným.
S nástupom sálových a neskôr osobných počítačov bolo možné získať tisíce partikulárnych riešení v oveľa kratšom čase ako dovtedy, pričom algoritmus grafického postupu vykresľovania trajektórie zostal vpodstate rovnaký. V ďalšom, keď budeme hovoriť o výpočte HP pomocou PC, pôjde o výpočet trajektórií realizovaný metódou Runge – Kutta 4. rádu. Riešiť sa bude systém troch diferenciálnych rovníc.
S postupne narastajúcim výpočtovým výkonom počítačov bolo možné uskutočňovať čoraz náročnejšie a objemnejšie výpočty trajektórií a rezov HP, čo malo za následok aj možnosť detailnejšej analýzy i viac graficky ilustratívnejšieho vysvetlenia prebiehajúcich dejov v obvode. Aj keď ide vpodstate stále o používanie už zmienenej metódy Runge – Kutta 4. rádu spolu s ďalšími podpornými podprogramami, vo všeobecnosti je možné využívať na výpočty trajektórií a rezov HP, nasledovné technologické prostriedky:
- osobný počítač s jedným resp. s viacjadrovým procesorom,
- technológia GRID a
- technológia GPGPU.
V tomto príspevku sa zmienime o možnostiach výpočtu osobným počítačom.
Využitie osobného (jednoprocesorového) počítača
Po dobe veľkých sálových počítačov sa stal osobný počítač pomerne rýchlo dostupným pre širšiu verejnosť. Objem výpočtov bolo možné zvyšovať s rastúcim výkonom CPU počítača i so zmenou architektúry CPU. Takto autor práce mal možnosť postupne zvyšovať objem výpočtov počnúc procesorom 286 až po súčasnosť. Výsledky simulácií boli publikované napr. v prácach [1], [15] – [17]. Programy boli vytvorené v jazyku C a ku zvýšenej rýchlosti výpočtov prispievali aj stále sa vyvíjajúce prekladače jazyka C. Keď si uvedomíme, že rýchlosť procesora sa zvyšovala zo 16 MHz po súčasných bežne dostupných 2800 MHz a viac, zrýchlenie výpočtov je zrejmé. Sumárne je možné povedať, že na zrýchlenie výpočtov pri použití jednoprocesorových počítačov mali vplyv:
- frekvencia CPU,
- prekladače jazyka C a
- architektúra CPU.
Tab. 1 ilustruje porovnanie rýchlosti výpočtu jednej trajektórie pri použití rôznych typov CPU, prekladačov (kompilátorov) ale aj architektúr CPU. Údaje boli zbierané od roku 1994. V stĺpci Prekladač skratky znamenajú:
- VC – Visual C, ver. 5.0 (používaný pod operačným systémom Windows),
- Djgpp – MS DOS-ovský 32 – bitový prekladač, ktorého *.exe súbor bolo možné spustiť pod Windows,
- Borland – Prekladač pracujúci pod operačným systémom MS DOS vo verzii 3.1. Výsledný *.exe súbor bolo tiež možné spustiť aj pod OS Windows 98, 2000 a XP.
Tab. 1 Porovnanie rýchlosti výpočtu jednej trajektórie pre rôzne CPU a prekladače.
| Por. č. | Typ CPU | frekvencia CPU [MHz] | Prekladač | ||
|---|---|---|---|---|---|
| VC [s] | Djgpp [s] | Borland [s] | |||
| 1. | Intel 486 | 120 | 95 | 115 | 185 |
| 2. | AMD K5 | 90 | 50 | 70 | 85 |
| 3. | AMD 486 | 133 | 43 | 50 | 90 |
| 4. | Cyrix IBM | 150 | 25 | 30 | 55 |
| 5. | Intel Pentium | 100 | 20 | 30 | 60 |
| 6. | Cyrix IBM | 200 | 20 | 25 | 57 |
| 7. | WinChip | 200 | 19 | 35 | 45 |
| 8. | Intel Pentium | 120 | 17 | 25 | 50 |
| 9. | Intel Pentium | 133 | 15 | 20 | 35 |
| 10. | AMD K6 MMX | 166 | 15 | 23 | 50 |
| 11. | Cyrix IBM | 233 | 15 | 19 | 33 |
| 12. | Intel Pentium | 150 | 13 | 20 | 40 |
| 13. | Intel Pentium | 166 | 12 | 19 | 36 |
| 14. | Intel Pentium MMX | 166 | 12 | 16 | 36 |
| 15. | AMD K6 MMX | 233 | 12 | 17 | 38 |
| 16. | Intel Pentium MMX | 200 | 10 | 15 | 35 |
| 17. | Intel Pentium Pro | 200 | 9 | 15 | 35 |
| 18. | Intel Pentium II | 266 | 7 | 10 | 24 |
| 19. | Intel Pentium III | 450 | 5 | 7 | 15 |
| Zrýchlenie: Por.č.1 / Por.č.19 | 19x | ~ 16x | ~ 12x | ||
V súčasnosti je možné použiť na vytvorenie spustiteľného súboru *. exe pod OS Windows softvér Bloodshed Dev-C++ a pod OS Linux je zasa vhodný prekladač gcc s možnosťou nastavenie rôznych optimalizácii, ktoré tiež môžu urýchliť výpočet rezov HP. Pod novým OS Windows 7 sa javí ako výhodný prekladač Bloodshed Dev-C++, ktorý síce ako 32 – bitový softvér vytvorí vo verzii 4.9.9.2 spustiteľný súbor aj pod Windows 7 avšak s využitím len jedného CPU. V lete 2012 autor článku testoval iba jeden 64 – bitový prekladač mingw 4.6.2, ktorý síce využíval obe jadrá procesora Intel Core2 spolu na 67% (oproti 50% v predchádzajúcom prípade), avšak ako prekladač resp. spustiteľný *.exe súbor, bol v konečnom dôsledku pri výpočte toho istého rezu HP viac ako 2x pomalší ako už spomínaný Bloodshed Dev-C++ využívajúci 1 jadro CPU.

Obr.2 Porovnanie rýchlosti výpočtu jednej trajektórie pre rôzne CPU a prekladač Djgpp pre údaje z tab. 1
Z Tab.1 je zrejmé, že:
- zmena architektúry zo 486 (Por. č.1 a 3) na AMD K5 (Por. č. 2) prinieslo zrýchlenie výpočtov, ale výkonovo ešte lepší z procesorov radu 586 v porovnaní AMD K5 & Intel, je CPU Intel Pentium 100 MHz (Por. č. 5),
- procesor rady 486 od AMD (Por. č. 3) bol rýchlejší ako jeho konkurent od firmy Intel (Por. č. 1) čo je opäť vplyv architektúry CPU,
- procesory Cyrix IBM (Por. č. 4, 6 a 11) resp. WinChip (Por. č. 7) výkonnostne zaostávali napriek vyšším, alebo rovnakým frekvenciám CPU v porovnaní s Intel Pentium 100 a 120 MHz (Por. č. 5 a 8), 166 a 200 MHz (Por. č. 14 a 16 – 17),
- použitím CPU Intel Pentium 120 ÷ 450 MHz (Por. č. 8, 9, 12, – 14, 16 – 19) sa úmerne skracuje čas výpočtu s rastúcou frekvenciou CPU,
- procesory rady K6 od AMD (Por. č. 10 resp. 15) boli pomalšie ako CPU Intel Pentium, Pentium Pro i Pentium MMX (Por. č. 9, 12 – 14, 16, 17) v dôsledku inej architektúry CPU,
- najrýchlejší program na výpočet trajekórie bol vytvorený prekladačom VC.
Pri testoch novších, výkonnejších aj viacjadrových CPU boli od roku 2004 testované pod OS Windows, PC s CPU uvedenými v tab. 2, programom vytvoreným Bloodshed Dev-C++, ktorý vypočítaval jeden a ten istý rez HP. Pri výpočte jeden rez HP pozostával zo 440×440 bodov – začiatočných podmienok, čo je spolu 193 600 trajektórií.. Pre každú Z výsledkov je zrejmý veľký nárast výpočtového výkonu v porovnaní s napr. CPU Intel Pentium 133 MHz, Celeron 500 MHz, či Pentium III 600 MHz uvedených v závere tab. 2 ako Por.č. 17, 20 a 21. Z tab. 2 vyplýva, že:
- pri dnešnom objeme výpočtov sú CPU uvedené v riadkoch 16 ÷ 21 nepoužiteľné a to i napriek tomu, že sú v nich zahrnuté pomerne nové PC typu All-in-one resp. 10“ netbook. Výsledky ukazujú, že nie sú vôbec vhodné na výpočet 2D rezov HP,
- staršie CPU od AMD (Por. č. 11 ÷ 13 a 15 ), pri súmeriteľných frekvenciách CPU v porovnaní s CPU Celeron (Por. č. 14), boli na výpočty rezov HP oveľa vhodnejšie nielen čo sa týka rýchlosti výpočtu, ale aj ceny CPU resp. PC. Podobné výsledky svedčiace o podstatne väčšej výkonnosti CPU od AMD oproti Intel-u, boli zistené pri výpočte iných rezov HP, ktoré neuvádza tab. 2.2, kedy ten istý rez HP, vypočítal PC s CPU Duron 650 MHz rovnako rýchlo ako PC obsahujúci CPU Intel Pentium IV 1700 MHz. V súvislosti s vplyvom zmeny architektúry CPU je potrebné tiež poznamenať, že taktiež aj nová architektúra CPU Pentium II priniesla zlepšené výsledky v rýchlosti rátania toho istého rezu HP na CPU Celeron 266 MHz v porovnaní s CPU Pentium 233 MHz až 1,75 násobne,
- nová architektúra viacjadrových CPU od firmy Intel s nástupom CPU Core2 a novších však znovu odsúva CPU od AMD ako nie veľmi vhodné na výpočet rezov HP. O tom svedčí aj porovnanie CPU Phenom (Por. č. 8 ) a Turion (Por. č. 11) s rovnako starými alebo novšími CPU v riadkoch 1 až 7 a 9,
- najnovšia architektúra CPU Intel i7 (Por. č. 1) a i3 (Por. č. 2) v porovnaní s predchádzajúcou generáciou CPU Core2 (Por. č. 3 ÷ 7 a 9) resp. Core Duo (Por. č. 10) je najvhodnejšia na výpočet rezov HP. Pri najnižšej taktovacej frekvencii CPU 2200 MHz, je procesor i7 lepší ako všetky CPU Core2 dokonca s frekvenciou CPU blížiacou sa ku 3000 MHz.
Tab. 2 Porovnanie rýchlosti výpočtu jedného rezu HP pre rôzne CPU použitím prekladača Bloodshed Dev-C++ ver. 4.9.9.2.
| Por. č. | Typ CPU | frekvencia CPU [MHz] | čas [min] | čas [hod] |
|---|---|---|---|---|
| 1. | i7 2670QM – notebook (NB) | 2200 | 43 | 0,72 |
| 2. | i3 550 | 3200 | 43 | 0,72 |
| 3. | Core2 E7500 | 2930 | 57 | 0,95 |
| 4. | Core2 Quad Q9550 | 2830 | 58 | 0,97 |
| 5. | i3 M550 – NB | 2270 | 70 | 1,17 |
| 6. | Core2 Q9550 | 2390 | 80 | 1,33 |
| 7. | Core2 E6550 | 2330 | 82 | 1,37 |
| 8. | Phenom X4 | 2600 | 88 | 1,47 |
| 9. | Core2 E6320 | 1860 | 102 | 1,70 |
| 10. | Core Duo T2450 – NB | 2000 | 102 | 1,70 |
| 11. | Turion X2 DualCore RM-72 – NB | 2100 | 110 | 1,83 |
| 12. | Sempron | 2000 | 116 | 1,93 |
| 13. | Duron | 1800 | 133 | 2,22 |
| 14. | Celeron | 2400 | 146 | 2,43 |
| 15. | Athlon | 1200 | 195 | 3,25 |
| 16. | Celeron All-in-one | 600 | 362 | 6,03 |
| 17. | Pentium III | 600 | 402 | 6,70 |
| 18. | Atom N270 All-in-one | 1600 | 443 | 7,38 |
| 19. | Atom N270 – 10“ NB | 1600 | 453 | 7,55 |
| 20. | Celeron | 500 | 482 | 8,03 |
| 21. | Pentium | 133 | 3960 | 66,00 |
Zhrnutie tabuľkového porovnania výkonnosti CPU je na obr. 3 vo forme stĺpcového grafu. Tam však kvoli prehľadnosti je vynechaný CPU Pentium 133 MHz, ktorý by svojim 66 hodinovým stĺpcom zneprehľadnil graf.
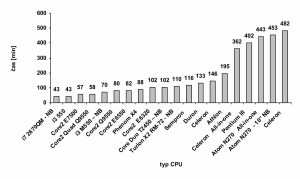
Obr. 3 Porovnanie rýchlosti výpočtu jedného rezu HP pre rôzne CPU, použitím prekladača Bloodshed Dev-C++ ver. 4.9.9.2
Vzhľadom na to, že prvé dva CPU v tab. 2 (i7 resp. i3) majú 4 jadrá / 8vlákien resp. 2 jadrá / 4vlákna, čo sa užívatelovi po spustení Správcu úloh systému Windows, javí ako 8 CPU resp. 4 CPU, bol urobený ešte jeden test týchto najrýchlejších CPU spolu s CPU Core2 Quad obsahujúci 4 jadrá. Súčasne boli spustené 2 programy na výpočet rezov HP, potom 4 a nakoniec súčasne 8 (iba pre CPU i7) s nastavením afinity – 1 program/1 CPU. V tejto súvislosti je potrebné poznamenať, že ak nebola nastavená afinita, výpočet rezov HP sa predĺžil iba o približne 2 – 3 minúty. Výsledky, včítane údajov z tab. 2 pre 1 CPU, sú zhrnuté v tab. 3, z ktorej vyplýva, že:
- CPU Core2 Quad ráta rovnako rýchlo rezy HP bez ohľadu na počet využitých jadier procesora,
- CPU i7 a i3 sú rýchle pri využití 1 ÷ 2 jadier – čas výpočtu do 46 min.,
- v prípade CPU i7 je čas výpočtu s využitím štyroch jadier rovnaký ako pre CPU Core2 Quad,
- pomalší čas výpočtu rezov HP pri použití i7 a i3, je síce pri využití všetkých vlákien procesorov i7 a i3 (96 min a 75 min), avšak v prípade i7 je aj čas 96 min akceptovateľný vzhľadom na to, že súčasne, počas 96 minút, je možný výpočet až 8 rezov HP! Ako teda ukazuje tab. 3, súčasné využitie všetkých 8 vlákien v CPU Intel i7 je najefektívnejšie, lebo ak by sme chceli vypočítať osem rezov HP iba s použitím 4 jadier CPU, čas výpočtu 4 rezov HP (58 min) by sa vlastne zdvojnásobil. Takto 8 rezov HP by v konečnom dôsledku bolo vypočítaných za 2 x 58 min = 116 min. Tento čas je teda o 20 min pomalší ako pri využití všetkých 8 vlákien CPU Intel i7. Podobne komentovať by bolo možné aj čas výpočtu 4 rezov HP využitím procesora Intel i3.
Tab. 3 Porovnanie rýchlosti výpočtu súčasne spustených 1, 2, 4 resp. 8 programov na výpočet rezov HP procesorov z tab. 2, Intel i7, i3 a Core2 Quad
| Počet „CPU“ | CPU & čas výpočtu [min] | ||
|---|---|---|---|
| i7 | i3 | Core2 Quad | |
| 1 | 43 | 43 | 58 |
| 2 | 44 | 46 | 58 |
| 4 | 58 | 75 | 58 |
| 8 | 96 | – | – |
Záver
Ako vyplýva z vyššie uvedených niekoľkých testov a postrehov získaných v priebehu posledných takmer 20 rokov, architektúra CPU, ale aj kvalitné prekladače jazyka C, výrazne urýchľujú výpočty potrebných rezov HP pre 3D zobrazenie, bez ďalšieho zvyšovania frekvencie CPU, ktorá je dnes obmedzená hranicou takmer 4000 MHz. Aj keď dnes existujú výkonnejšie CPU oproti testovanému Intel i7 2670 napr. Core i7 3960X obsahujúcich 6 jadier / 12 vlákien, Xeon E5-2687 obsahujúcich 8 jadier / 16 vlákien, resp. možno aj AMD Opteron 6282 so 16 jadrami, ich ceny v čase písania článku sú: 1000 €, 1800 € resp. 1000 €. Do budúcna sa však javí zaujímavou možnosťou radšej využiť (možno) menej výkonný CPU AMD Opteron 6282, ktorý však so 16 jadrami môže poskytnúť podobný výkon ako takmer 2x drahší Xeon E5-2687 s iba 8 jadrami / 16 vláknami CPU.
Poďakovanie
 Podporujeme výskumné aktivity na Slovensku/ Projekt je spolufinancovaný zo zdrojov EÚ. Tento článok bol vypracovaný v rámci projektu “Centrum excelentnosti integrovaného výskumu a využitia progresívnych materiálov a technológií v oblasti automobilovej elektroniky”, ITMS 26220120055.
Podporujeme výskumné aktivity na Slovensku/ Projekt je spolufinancovaný zo zdrojov EÚ. Tento článok bol vypracovaný v rámci projektu “Centrum excelentnosti integrovaného výskumu a využitia progresívnych materiálov a technológií v oblasti automobilovej elektroniky”, ITMS 26220120055.
Literatúra
- ŠPÁNY, Viktor et al.: The calculation of symmetrizing voltage in flip flop sensors. In: Radioelectronics. Košice: FEI TU, 1994, s. 22-27.
- GUZAN, Milan: Boundary surface of a ternary memory in the absence of limit cycles In: Radioelektronika 2012: Proceedings of 22nd International Conference, Brno, April 17-18, 2012, Czech Republic, p. 1-4. ISBN 978-80-214-4469-0.
- ŠPÁNY, Viktor et al.: Chua’s singularities: Great miracles in circuit theory. In: International Journal of Bifurcation and Chaos, vol. 20, 2010, no. 10, p. 2993-3006.
- SOBOTA, Branislav – GUZAN, Milan: Rekonštrukcia hraničnej plochy Chuaovho obvodu. In: SEKEL 2010: mezinárodní konference učitelů elektrotechniky, Liberec, Malá Skála, 15. – 17. září 2010: sborník příspěvků z konference. Liberec: TU v Liberci, 2010, s. 151-156.
- SOBOTA, Branislav: 3D modelling of Chua`s circuit boundary surface In: Acta Electrotechnica et Informatica, roč. 11, 2011, č. 1, s. 44-47.
- ŠPÁNY, Viktor: The Simple VA Characteristics Approximation and the Complex Analysis of the Tunnel Diode Oscillator. In: Proceedings of the IEEE, vol. 55, 1967, No.9, p. 1641-1643.
- ŠPÁNY, Viktor: Výpočet parametrov medzných cyklov pre obvod s tunelovou diódou. In: Elektrotechnický časopis, roč. 19, 1968, č. 1, s. 21-33.
- ŠPÁNY, Viktor: Grafické riešenie nelineárneho obvodu metódou m-rozmerného fázového priestoru. In: Elektrotechnický časopis, roč. 20, 1969, č. 4, s.233-248.
- ŠPÁNY, Viktor: Približný výpočet amplitúd limitných cyklov pre obvod s n-reaktančnými prvkami. In: Zborník vedeckých prác VŠT v Košiciach, zv. 1, 1970, s. 65-79.
- ŠPÁNY, Viktor: Špeciálne plochy a trajektórie trojrozmerného stavového priestoru. In: Acta Polytechnica, 12, III-1976-2, s. 231-242.
- ŠPÁNY, Viktor: Multistabilné systémy a špeciálne plochy m-rozmerného stavového priestoru. In: Elektrotechnický časopis, roč. 33, 1982, č. 7, s. 551-556.
- BREPTA, R.: Grafické metódy pre riešenie dynamických problémov. In: Strojnoelektrotechnický časopis, roč. VIII, 1957, č. 6, s.417-424.
- ŠPÁNY, Viktor: The Analysis of the One-Tunnel Diode Binary. In: Proceedings of the IEEE, vol. 55, 1967, No. 6, p. 1089-1090.
- SCHAPPER, M. A.: Monostable Behaviour of an LR Loaded Tunnel Diode with Two Stable States. In: Proceedings of the IEEE, vol. 56, 1968, No. 1, p. 91-92.
- ŠPÁNY, Viktor – GALAJDA, Pavol – GUZAN, Milan: Boundary surfaces of One-Port memories. In: Tesla III Milenium Conference, Belehrad, 1996, s. IV-131 – 137.
- GALAJDA, Pavol – ŠPÁNY, Viktor – GUZAN, Milan: The state space mystery with negative load in multiple-valued logic. In: Radioengineering, vol. 8, 1999, no. 2, p. 2-7.
- ŠPÁNY, Viktor – GALAJDA, Pavol – GUZAN, Milan: The state space mystery in multiple-valued logic circuit with load plane – part I. In: Acta Electrotechnica et Informatica, roč. 1, 2001, č. 1, s. 17-22.

