Porovnanie metód riadenia prístupu založených na meraní

28. September, 2012, Autor článku: Pištek Michal, Elektrotechnika, Informačné technológie
Ročník 5, číslo 9 This page as PDF Pridať príspevok

Metódy riadenia prístupu (AC) majú v IP sieťach dôležitú úlohu z hľadiska prevencie zahltenia siete a zabezpečenia čo najväčšieho využitie prostriedkov danej siete. Článok sa zameriava na riadenie prístupu založenom na meraní (MBAC), pričom je tu zhrnutých niekoľko používaných MBAC algoritmov. Dané algoritmy sú tu porovnávané pri rôznych sieťových scenároch s rozličnými druhmi prevádzky.

Úvod

Aby bolo možné poskytnúť požadované QoS danému toku, sieť musí monitorovať využitie jej zdrojov. Sieť by mala zamietnuť požiadavku o rezerváciu časti zdrojov, ak dané zdroje nie sú dostupné. Mechanizmus AC toto vykoná ako súčasť procesu rezervácie. Pred tým ako môže byť požiadavka na rezerváciu zdrojov akceptovaná, musí táto požiadavka prejsť AC testom. AC má dve základné funkcie. Prvá funkcia určuje, či môže byť nový tok pripustený s ohľadom na metódu AC. Druhá funkcia monitoruje a vykonáva merania na dostupných zdrojoch.

Najbežnejším rozdelením riadenia prístupu je rozdelenie podľa mechanizmu určenia, či je v danej sieti dostatočné množstvo prostriedkov na pripustenie toku dát [1]: Paramter-based admission control (PAC), Probe-based admission control (PBAC) a Measurement-based admission control (MBAC). MBAC sa ukázal ako ideálny spôsob riadenia prístupu pre dátové toky nevyžadujúce garantované služby a ktoré tolerujú istý stupeň oneskorenia a straty paketov. Vyvinulo sa množstvo rôznych algoritmov s cieľom nájsť to ideálne riešenie. MBAC na rozdiel od iných metód nepotrebuje apriórnu charakterizáciu siete, ale spolieha sa na merania a pomocou nich vykonáva riadenie prístupu.

1. Riadenie prístupu založené na meraní (MBAC)

MBAC sa nespolieha na apriórnu charakterizáciu siete. Namiesto toho sa spolieha na merania aktuálneho zaťaženia prevádzky a to potom využíva pri rozhodovaní o povolení prístupu. Keďže zdroje prevádzky nie sú statické, MBAC má probabilistický prístup a nemalo by byť používané pri poskytovaní pevnej QoS. Avšak pre zdroje zhlukovej prevádzky a aplikácie, ktoré dokážu tolerovať istý stupeň kolísania oneskorenia, MBAC poskytuje dobrý kompromis medzi poskytovanou QoS a využiteľnosťou siete. Vďaka štatistickému multiplexovaniu sa využiteľnosť siete podstatne zvyšuje pri veľkom počte dátových tokov.


Obr. 1. Model MBAC.

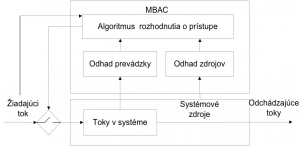
MBAC algoritmus zahŕňa tri elementy [2]: algoritmus rozhodnutia o prístupe (admission decision algorithm), odhad prevádzky (traffic estimator) a odhad zdrojov (resource estimator). MBAC algoritmus meria prevádzku v systéme a zostávajúce systémové zdroje, ako dostupná šírka pásma a veľkosť buffera. Na základe meraní odhad prevádzky určí koľko prevádzky je v systéme, aká je jej charakterizácia a koľko tokov sa nachádza v systéme. Odhad zdrojov určí, koľko zdrojov sa nachádza v systéme. Keď nový tok požaduje prístup do systému, MBAC algoritmus využije algoritmus rozhodnutia o prístupe pri rozhodnutí, či daný tok pripustiť. Toto rozhodnutie je založené na vstupoch z odhadu prevádzky a odhadu zdrojov. Okrem toho sa ešte spolieha na údaje poskytnuté tokom, ako napríklad jeho QoS požiadavky a jeho vlastnosti prevádzky.

2. MBAC algoritmy

V tejto časti sa zameriam na analýzu štyroch MBAC algoritmov.

2.1. Odmeraná suma

Algoritmus Odmeraná suma používa merania, aby určil záťaž existujúcej prevádzky. Algoritmus pripustí nový tok ak je nasledujúci test úspešný [3]:

\hat{v}+r^\alpha < \nu \mu[/latex]</td> <td style="width:20px; text-align:center;">(1)</td> </tr> </table> <p align="justify">Kde <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\hat{v} je odmeraná záťaž existujúcej prevádzky, rα je maximálna prenosová rýchlosť nového toku α, μ je šírka pásma linky a υ je užívateľom definovaná cieľová využiteľnosť. Ako odhad prevádzky sa používa časové okno. Po pripustení nového toku sa odhad záťaže dočasne zvýši použitím \hat{v}'=\hat{v} + r^\alpha. Toto dočasné zvýšenie je odobraté, keď je vyhotovený nový odhad záťaže existujúcej prevádzky.


Obr. 2. Priebeh odhadu prevádzky časové okno.

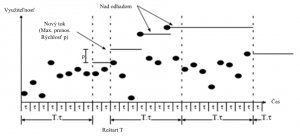
Každú τ vzorku sa vypočíta priemerná záťaž. Na konci meracieho okna T sa následne využije najvyššia hodnota z tohto okna ako odhad záťaže pre ďalšie okno. Ako náhle sa pripustí nový tok, nastáva reštart okna. Nový odhad sa zvýši o maximálnu prenosovú rýchlosť tohto toku.

2.2. Ekvivalentná šírka pásma

Ekvivalentná šírka pásma je definovaná ako šírka pásma C(ε) taká, že stacionárne požiadavky šírky pásma skupiny tokov prekročia túto hodnotu s pravdepodobnosťou nanajvýš ε. Ekvivalentná šírka pásma založená na Hoeffdingových hraniciach \hat{C_H} sa vypočíta ako [3]:

\hat{C_H}(\hat{\nu},\{ p_i \}_{1 \leq i \leq n},\epsilon) = \hat{v}+\sqrt{\frac{ln(1/\epsilon) \sum_{i=1}^n (p_i)^2}{2}} (2)

Kde \hat{v} je odmeraná priemerná prenosová rýchlosť príchodu existujúcej prevádzky a ɛ pravdepodobnosť, že táto rýchlosť prekročí kapacitu linky. Odmeraná priemerná prenosová rýchlosť príchodu môže byť aproximovaná odmeranou priemernou záťažou. Test riadenia prístupu, keď nový tok α žiada o prístup je:

\hat{C_H} + p^\alpha \leq \mu (3)

Kde pα je maximálna prenosová rýchlosť nového toku α a μ je šírka pásma linky. Po pripustení nového toku sa výpočet záťaže zvýši:

\hat{v}' = \hat{v} + p^\alpha (4)

Ak nie je známa maximálna prenosová rýchlosť toku, opäť sa využívajú parametre token bucket filtra. Ako odhad prevádzky sa používa exponenciálne priemerovanie. Využíva odhad priemernej rýchlosti príchodu namiesto okamžitej šírky pásma pre dosiahnutie rozhodnutia o prístupe. Priemerná rýchlosť príchodu ν ̂^S je odmeraná každú S vzorkovaciu periódu. Priemerná rýchlosť príchodu je potom vypočítaná pomocou funkcie s nekonečnou impulzovou odpoveďou s váhou w:

\hat{v}' = (1-w)\hat{v} + w \hat{v}^s (5)

Väčším w sa dosiahne adaptívnejší priemerovací proces na zmeny zaťaženia. Menšie w má za následok hladkejší priebeh priemeru vďaka udržiavaniu dlhšej histórie hodnôt. Menšie S robí meranie citlivejším na zhluky. Väčšie S má za následok nižšie priemery, kde proces priemerovania je vyvolaný menej často.

2.2. Akceptačná oblasť

Akceptačná oblasť vo [4] využíva výpočty pomocou Chernoffových hraníc. Tu je ekvivalentná šírka pásma On/Off zdroja vypočítaná pomocou nasledovnej rovnice:

\alpha_k (s) = \frac{1}{s} log \left [ 1+ \frac{m_k}{h_k} (e^{sh_k}-1) \right ] (6)

Kde mk reprezentuje priemernú prenosovú rýchlosť a hk maximálnu prenosovú rýchlosť. Parameter s (s>0) sa nazýva priestorový parameter, určujúci asymptotický exponenciálny pokles rýchlosti pravdepodobnosti koncovej distribúcie dĺžky radu s ohľadom na veľkosť radu. Krivka ekvivalentnej šírky pásma závisí od priemernej prenosovej rýchlosti na x-ovej osi a výslednej ekvivalentnej šírky pásma na y-ovej osi. Lineárna hranica v rôznych bodoch na tejto krivke sa dá vypočítať ako dotyčnica v tomto bode:

c+\alpha \hat{v} \leq \mu (7)

Kde c určuje miesto a α sklon dotyčnice. Táto lineárna hranica môže byť potom použitá ako MBAC algoritmus. Patria tu [5]:

Dotyčnica vo vrchole (Tangent at peak)

Tento algoritmus je založený na dotyčnici vo vrchole krivky ekvivalentnej šírky pásma vypočítanej z Chernoffových hraníc. Nový tok je pripustený, ak je splnená nasledujúca podmienka:

np(1-e^{-sp}) + e^{-sp} \hat{v} \leq \mu (8)

Kde n je počet pripustených tokov, p je maximálna prenosová rýchlosť tokov, s je parameter Chernoffových hraníc, ν ̂ je odhad aktuálnej záťaže a μ je šírka pásma linky.

Dotyčnica v počiatku (Tangent at origin)

Algoritmus využíva dotyčnicu krivky ekvivalentnej šírky pásma v počiatku. Nový tok je pripustený ak platí:

e^{sp} \hat{v} \leq \mu (9)

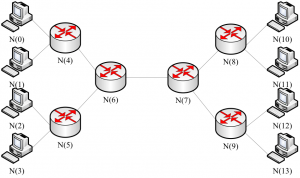
Ako odhad prevádzky sa používa bodové vzorkovanie.
Jedná sa o techniku bez pamäti predchádzajúcich hodnôt. Odhad sa vykonáva len z aktuálneho stavu v sieti. Je to teda mechanizmus merania, ktorým sa každú S periódu získava vzorka priemerného zaťaženia.

3. Simulácie výkonnosti MBAC algoritmov

Pre porovnanie výkonnosti jednotlivých algoritmov MBAC som vychádzal z príkladov a testovacích scenárov, ktoré sa nachádzajú v rámci nainštalovanej verzie NS 2.35. Simulácie jednotlivých algoritmov som vykonával na Intserv linke, kde som využil jednu triedu riadenej záťaže. Topológia zapojenia je znázornená na obr. 3.


Obr. 3. Topológia simulovanej siete.

Nachádzajú sa tu štyri vysielacie stanice a štyri prijímacie stanice. Medzi nimi sa nachádza niekoľko spojovacích prvkov, kde medzi bodmi 6 a 7 sa nachádza daná Intserv linka.

3.1. Parametre siete

Celá simulácia vždy trvá 200 s, kde merať sa začne až po 100 s, keď už je stav siete ustálený. Pre danú sieť som medzi linkami využil jednotnú šírku pásma 10 Mbit/s s oneskorením 1 ms. Jednotlivé toky prichádzajú s odstupom náhodnej veličiny s priemerom 0,5 s a dĺžka ich pobytu v sieti je daná náhodnou veličinou s priemernou hodnotou 150 s. Zdroje sú popísané token bucket filtrom s parametrami r=64 kbit/s a b =1, z nich si jednotlivé algoritmy potom sú schopné vypočítať prenosovú rýchlosť novo prichádzajúceho toku.

Prevádzkový generátor na jednotlivých zdrojoch prevádzky je popísaný exponenciálnym rozdelením s parametrami: veľkosť paketu je 200 bytov, daný generátor je typu On/Off, teda striedajú sa doby vysielania a nečinnosti zdroja, kde pre oba intervaly som vyčlenil po 100 ms, kde počas On intervalu zdroj vysiela s rýchlosťou 64 kbit/s. Na dané simulácie sa teda dá pozerať aj ako na simulácie VoIP hovorov, keďže tie majú exponenciálny charakter.

Okrem tohto generátora používam ešte On/Off zdroj prevádzky s Paretovým rozdelením (rovnaké doby vysielania, nečinnosti a veľkosť paketu) a zdroj konštantnej prevádzky (rovnaká veľkosť paketu s konštantným vysielaním 64 kbit/s). Pri jednotlivých simuláciách používam pri jednotlivých štyroch vysielačoch vždy len jeden druh prevádzkového generátora. Jednotlivé štyri zdroje prevádzky začínajú vysielať v druhej, tretej, štvrtej, respektíve piatej sekunde.

3.2. Odmeraná suma (MS)

Tento najjednoduchší MBAC algoritmus ponúka optimalizovanie výkonnosti pomocou parametra využiteľnosti, ktorým sa určí horná hranica požadovanej využiteľnosti. Ďalší parameter, ktorý je tu možno meniť a optimalizovať je dĺžka časového okna odhadu prevádzky. V tabuľke 1 je znázornený vzťah veľkosti časového okna T ku využiteľnosti linky a stratám paketov. Priemerná rýchlosť sa vypočítava každých S=0,5 s pri nastavenej hodnote využiteľnosti 0,98.

Tab. 1. Vplyv parametra T na vlastnosti algoritmu MS.

T [s] 1 2 3 4
Využ. [%] 95,88 92,92 91,79 90,64
Straty [%] 3,69.10-2 1,07.10-3 7,85.10-4 0

Z daných údajov vyplýva fakt, že čím je časové okno väčšie, tým sa správa konzervatívnejšie a nedokáže dostatočne rýchlo reagovať na zmeny prevádzky, čo má potom za následok aj nižšiu využiteľnosť. Na druhej strane ale obmedzuje stratovosť paketov. Ďalej som sa zameral na ďalší parameter, ktorý je vhodné sledovať pri riadení prístupu a to pomer odmietnutia, ktorý predstavuje pomer nepripustených tokov ku všetkým tokom, ktoré sa pokúsili o pripustenie. Nasledujúca tabuľke ilustruje situáciu, kde pri veľkosti časového okna T=2 s sa postupne mení užívateľská využiteľnosť od 0,7 do 0,85.

Tab. 2. Sledovanie pomeru odmietnutia pri zmene parametra υ algoritmu MS.

υ 0,7 0,75 0,8 0,85
Využiteľnosť [%] 67,497 71,608 77,018 81,642
Pomer odmietnutia 0,712 0,671 0,656 0,6465

Z tabuľky 2 vyplýva, že pomer odmietnutia stúpa, čím je nižšie nastavená užívateľská využiteľnosť. To je logicky spôsobené faktom, že daná sieť parametrom υ obmedzuje svoju fyzickú šírku pásma a tým sa teda aj obmedzuje počet možných pripustených tokov a zvyšuje pomer nepripustených tokov.

3.3. Ekvivalentná šírka pásma (HB)

Algoritmu ekvivalentnej šírky pásma, respektíve Hoeffdingových hraníc umožňuje optimalizovať výkonnosť pomocou parametra ɛ, ktorý predstavuje pravdepodobnosť, že odmeraná priemerná záťaž prekročí kapacitu linky. Vzťah tohto parametra ku využiteľnosti a strate paketov je znázornený v tabuľke 3. Pre hodnoty v danej tabuľke bolo použité w=2-2

Tab. 3. Vplyv parametra ɛ na vlastnosti algoritmu HB.

υ 0,75 0,8 0,85 0,9
Využiteľnosť [%] 92,57 93,21 93,8 94,40
Straty [%] 0 2,2.10-3 3,14.10-3 4,26.10-3

Z tabuľky je zrejmé, že s rastúcim ɛ rastie aj využiteľnosť siete. To je spôsobené tým, že algoritmus pri vyššom ɛ ráta s tým, že toky prekročia odmeranú záťaž siete a teda nie je potrebné im zamedziť prístup ako pri nižšej pravdepodobnosti. Ďalej som simuláciami zisťoval, ako sa hodnoty využiteľnosti a stratovosti menia pri zmene parametra w. Pre hodnoty v danej tabuľke bolo použité ɛ =0,9.

Tab. 4. Vplyv parametra w na vlastnosti algoritmu HB.

w 2-1 3-1 2-2 5-1
Využ. [%] 95,72 94,84 94,4 93,78
Straty [%] 2,49.10-2 8,86.10-3 4,26.10-3 1,81.10-3

Čim je menší parameter w, tým sa zmenšuje aj využiteľnosť. Dôvodom k tomu je fakt, že menším w sa dlhšie udržujú hodnoty zaťaženia, kde sa medzi týmito hodnotami môže vyskytovať aj tok, ktorý už skončil vysielanie. Rovnako ako u MS, aj tu som sa zameral na pomer odmietnutia. Toto som simuloval pre w=2-5 pričom hodnotu ɛ som postupne menil od 0,05 do 0,95.

Tab. 5. Sledovanie pomeru odmietnutia pri zmene ɛ.

ɛ 0,05 0,3 0,75 0,95
Využiteľnosť [%] 71,545 74,615 77,781 79,14
Pomer odmietnutia 0,679 0,674 0,661 0,65

3.4. Akceptačná oblasť – Dotyčnica na počiatku (ACTO)

Pri algoritmoch akceptačnej oblasti sa ako optimalizačný parameter dá využiť priestorový parameter Chernoffových hraníc s, ktorý sa vypočítava miesto a sklon jednotlivých dotyčníc ku krivke ekvivalentnej šírke pásma. V tabuľke 6 je znázornený vzťah tohto parametra od využiteľnosti a stratovosti.

Tab. 6. Vplyv parametra s na vlastnosti algoritmu ACTO.

s 8.10-7 10.10-7 12.10-7 14.10-7
Využiteľnosť [%] 95,92 94,67 93,55 92,61
Straty [%] 3,94.10-2 8,11.10-3 2,95.10-3 2,69.10-3

Z tabuľky 6 vyplýva, že využiteľnosť siete stúpa, keď sa parameter s blíži k nule. To kvôli tomu, že vo vzťahu (9) sa esp blíži k jednotke a teda výsledný vzťah rozhodujúci o prístupe sa blíži k vzťahu \hat{v} \leq \mu, teda algoritmus pripúšťa toky až kým nie je dosiahnutá plná využiteľnosť siete. Tabuľka 7 znázorňuje, ako sa mení pomer odmietnutia pre tento algoritmus pre priestorový parameter s z intervalu 3.10-6 až 6.10-6.

Tab. 7. Sledovanie pomeru odmietnutia pre meniaci parametra s algoritmu ACTO.

s 3.10-6 4.10-6 5.10-6 6.10-6
Využiteľnosť [%] 83,827 78,636 73,979 69,511
Pomer odmietnutia 0,638 0,651 0,675 0,689

3.5. Akceptačná oblasť – Dotyčnica vo vrchole (ACTP)

Tak isto ako aj u Dotyčnice v počiatku aj pri Dotyčnici vo vrchole je použitý optimalizačný parameter s. V tabuľke 8 je znázornený vzťah tohto parametra od využiteľnosti a stratovosti.

Tab. 8. Vplyv parametra s na vlastnosti algoritmu ACTP.

s 8.10-7 10.10-7 12.10-7 14.10-7
Využiteľnosť [%] 95,99 95,75 93,75 92,81
Straty [%] 5,35.10-2 4,67.10-2 3,61.10-3 1,15.10-3

Rovnako ako aj u algoritmu ACTO, aj tu sa so znižujúcim parametrom s zvyšuje využiteľnosť siete. Vo vzťahu (8) sa e-sp takisto blíži k jednotke a rovnako ako v predchádzajúcom prípade aj tu sa výsledný vzťah rozhodnutia o prístupe blíži k \hat{v} \leq \mu. Tabuľka 9 znázorňuje, ako sa mení pomer odmietnutia pre tento algoritmus pre priestorový parameter s z intervalu 5.10-6 až 8.10-6.

Tab. 9. Sledovanie pomeru odmietnutia pre meniaci parametra s algoritmu ACTP.

s 5.10-6 6.10-6 7.10-6 8.10-6
Využiteľnosť [%] 79,527 76,983 74,517 72,293
Pomer odmietnutia 0,644 0,678 0,681 0,687

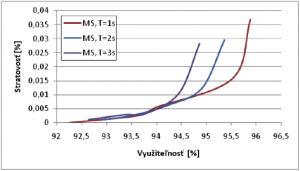
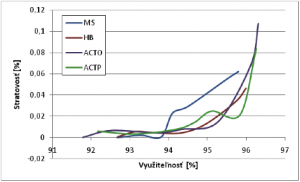
3.6. Porovnanie algoritmov

V tejto časti som sa zameral na porovnanie spomenutých algoritmov na základe nasledujúcich typov kriviek. Krivka, ktorá reprezentuje závislosť stratovosti paketov od využiteľnosti (ďalej len krivka stratovosti). Druhá krivka porovnania reprezentuje závislosť pomeru odmietnutia od využiteľnosti (ďalej len krivka odmietnutia). Nasledujúce simulácie predstavujú situáciu pri VoIP prevádzke. Jeden algoritmus môže mať rôzne krivky stratovosti v závislosti, ako dokážeme optimalizovať jeho parametre.

Algoritmy ako Odmeraná suma a Ekvivalentná šírka pásma okrem optimalizačných parametrov samotných algoritmov ako využiteľnosť u MS a epsilon u HB môžu meniť aj parametre svojich odhadov prevádzky ako veľkosť časového okna u MS a váha w u HB. Na obrázku 4 možno vidieť 3 rôzne krivky stratovosti MS algoritmu, kde pri fixnej hodnote časových okien som menil hodnotu požadovanej využiteľnosti υ. Aj z tohto obrázku je možné vidieť, že menšia dĺžka okna vedie k rýchlejším reakciám siete a tým sa znižuje aj stratovosť.


Obr. 4. Vplyv parametra T na krivku stratovosti.

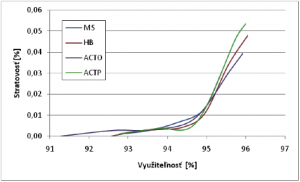
Samotné porovnanie algoritmov je znázornené na obrázku 5.


Obr. 5. Porovnanie algoritmov pri VoIP prevádzke na základe krivky stratovosti.

Z obrázka možno vidieť, že všetky algoritmy sa chovajú rovnako, z čoho vyplýva fakt, že pre zdroj prevádzky s exponenciálnym rozdelením môžu mať MBAC algoritmy pri optimalizovaní svojich parametrov rovnaké vlastnosti z hľadiska krivky stratovosti. Ďalší spôsob porovnania algoritmov, ktorý som využil je krivka odmietnutia. Daná krivka reprezentuje závislosť pomeru odmietnutia od využiteľnosti, kde pomer odmietnutia vypočítavam ako počet všetkých odmietnutých tokov ku celkovému počtu tokov, ktoré žiadali o prístup do systému. Z danej krivky možno vyčítať, ako algoritmus narába s novo prichádzajúcimi tokmi pri danej využiteľnosti. Pri danej využiteľnosti by mala byť snaha MBAC algoritmov odmietnuť čo najmenší počet tokov a tým pádom mať nižší pomer odmietnutia.

Na obrázku 6 je znázornené porovnanie použitých štyroch algoritmov. V tomto porovnaní som vychádzal z tabuliek 2, 5, 7 a 9, kde som sa snažil pomocou optimalizačných parametrov znázorniť všetky algoritmy na približne rovnakom intervale využiteľnosti 70-80 %.


Obr. 6. Porovnanie algoritmov pri VoIP prevádzke na základe krivky odmietnutia.

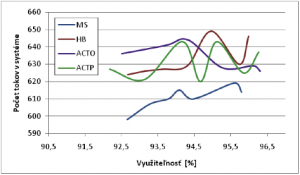
Dané krivky nie sú úplne totožné, kde najlepšie sa javí algoritmus MS, ktorý miestami dosahuje pre danú využiteľnosť pomer odmietnutia o jednu stotinu nižší ako u ostatných algoritmoch, situácia sa postupne ale vyrovnala, kde už sú rozdiely medzi algoritmami minimálne. S danou krivkou úzko súvisí aj krivka závislosti celkového počtu tokov v systéme od využiteľnosti.


Obr. 7. Porovnanie algoritmov pri VoIP prevádzke na základe pripustených tokov.

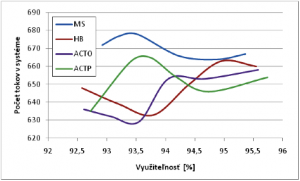
Aj z daného grafu je vidno, že algoritmy sa správajú veľmi podobne, kde po väčšinu intervalu sa javí ako najlepší algoritmus MS. Na danom intervale využiteľnosti je pre danú sieť u všetkých algoritmov nulová stratovosť. Preto som sa rozhodol uskutočniť simulácie počtu tokov v systéme na hodnotách využiteľnosti z obrázka 8. Tu už stratovosť nulová nie je a dá sa tu dať do súvisu výsledky z oboch grafov.


Obr. 8. Porovnanie algoritmov pri VoIP prevádzke na základe pripustených tokov 2.

Ako vidno, aj tu má algoritmus MS najlepšiu schopnosť pripustiť čo najväčší počet tokov do systému. Chybné pripustenie sa odrazí v stratách paketov a keďže krivky stratovosti sú u všetkých algoritmov prakticky rovnaké je možné prehlásiť, že algoritmus MS ponúka na základe mnou zvolených kritérií najoptimálnejšie riešenie. V ďalších simuláciách som sa zameral na porovnanie algoritmov pri zdroji prevádzky s Paretovým rozdelením, ktorým sa simuluje internetová (napríklad FTP) prevádzka. Algoritmy porovnávam na základe rovnakých kritérií ako pri simuláciách VoIP prevádzky. Pri grafe kriviek stratovosti som hodnoty optimalizačných parametrov algoritmov zachoval na hodnotách z predchádzajúceho prípadu.


Obr. 9. Porovnanie algoritmov pri FTP prevádzke na základe krivky stratovosti.

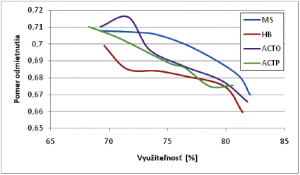
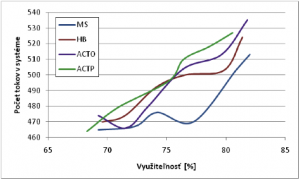
Z obrázka je zrejmé, že pri danom prípade sa algoritmy nesprávajú rovnako ako u zdroja s exponenciálnym rozdelením. Kde algoritmy HB, ACTO a ACTP majú približne rovnaký priebeh, no MS vykazuje pre dané využiteľnosti vyššiu stratovosť. Na danom intervale využiteľností som následne vykonal simulácie počtu tokov v systéme. Výsledný graf je na obrázku 10.


Obr. 10. Porovnanie algoritmov pri FTP prevádzke na základe pripustených tokov.

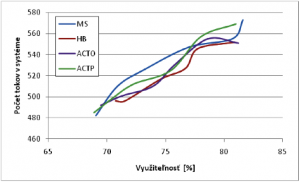
Ako možno vidieť algoritmy sa správajú opačne ako u zdroja prevádzky s exponenciálnym rozdelením. Tu sa javí ako najhorší algoritmus MS, ktorý do systému púšťa najmenší počet tokov. Podobné výsledky boli dosiahnuté aj pri využiteľnosti 70-80%.


Obr.11. Porovnanie algoritmov pri FTP prevádzke na základe krivky odmietnutia


Obr.12. Porovnanie algoritmov pri FTP prevádzke na základe pripustených tokov 2.

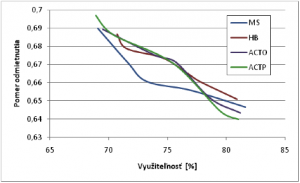
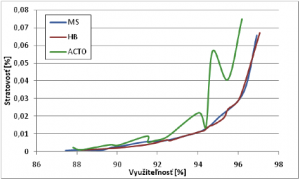
Aj dané grafy potvrdzujú, že algoritmus MS nedokáže prijať toľko tokov do systému ako ostatné algoritmy, z čoho aj vyplýva vyšší pomer odmietnutia daných tokov. Ostatné algoritmy sa správajú veľmi podobne, kde HB sa ukazuje ako najlepší pri grafe kriviek odmietnutia a ACTP pri grafe počtu tokov v systéme. Pri vyrovnaných výsledkov u predchádzajúcich grafov možno teda tieto dva algoritmy považovať za najlepšie pri danom type prevádzky.

Pri nasledujúcich simuláciách som využil prevádzkový generátor s konštantnou prevádzkou. Daný generátor generuje pakety veľkosti 200 bajtov so stálou rýchlosťou 64 kbit/s. Veľkosť radu na vstupnom uzle do IntServ linky som obmedzil z 80 na 20 paketov, aby som mohol porovnávať dané algoritmy aj z hľadiska stratovosti keďže pri veľkosti radu 80 vykazovali algoritmy nulovú stratovosť aj pri 95 % využiteľnosti.

Z daných štyroch MBAC algoritmov som vylúčil z porovnania algoritmus ACTP. To z dôvodu, že daný algoritmus prepúšťa prevádzku blížiacej sa 100% využiteľnosti linky pri ľubovoľnej zmene parametra s. Daná dotyčnica sa nachádza vo vrchole krivky ekvivalentnej šírky pásma a tá má konštantný priebeh takže daný algoritmus prepúšťa všetky toky, samozrejme až do plného využitia siete. Keďže má prevádzka konštantný charakter vo vzorci (8) platí, že np = \hat{v} teda daný vzorec sa upraví na tvar \hat{v} \leq \mu, kde teda algoritmus prepúšťa toky až kým sa odmeraná záťaž nerovná šírke pásma linky a už teda nezávisí od parametra s.

Zostávajúce tri algoritmy som následne porovnával podľa predchádzajúcich kritérií, kde na obrázku 13 je znázornený graf kriviek stratovostí daných algoritmov.


Obr.13. Porovnanie algoritmov pri konštantnej prevádzke na základe krivky stratovosti.

Z daného grafu možno vidieť, že algoritmy MS a HB majú prakticky totožný priebeh. Oproti tomu algoritmus ACTO spôsobuje najvyššiu stratovosť. Tento graf teda potvrdzuje fakt, že rovnako ako algoritmus ACTP, aj ACTO vychádza z predpokladov On/Off zdroja. Parameter s tu však oproti ACTP je relevantný (výraz esp sa v rovnici (9) nevykráti). Možno uňho teda očakávať najhoršie výsledky z daných troch algoritmov. Ako aj v predchádzajúcich prípadoch aj tu som následne vykonal simulácie na intervale využiteľnosti 70-80 %, kde som sa zameral na pomer stratovosti a pripustený počet tokov do systému.


Obr.14. Porovnanie algoritmov pri konštantnej prevádzke na základe krivky odmietnutia.


Obr.15. Porovnanie algoritmov pri konštantnej prevádzke na základe pripustených tokov.

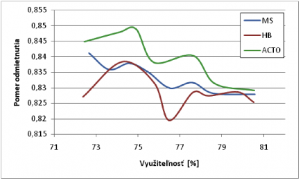
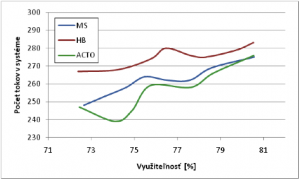
Výsledky z obrázkov 14 a 15 potvrdzujú, že pre konštantnú prevádzku sa algoritmus ACTO nehodí, keďže odmieta najviac tokov a teda do systému pripúšťa najmenej tokov. Zo zostávajúcich dvoch algoritmov sa najlepšie javí na základe oboch grafov algoritmus HB, ktorý prijíma o desať až dvadsať tokov viac ako algoritmus MS.

4. Záver

V danom článku som simuláciami skúmal správanie MBAC algoritmov pri rôznych druhoch prevádzky. Najskôr som sa zameral na správanie jednotlivých algoritmov pri zmene ich optimalizačných parametrov. Tu som sledoval ako sa pri ich zmene menia parametre využiteľnosť, stratovosť, pomer odmietnutia a pripustený počet tokov do systému. Algoritmy MBAC som ďalej porovnával z viacerých hľadísk. Pre zdroj prevádzky s exponenciálnym rozdelením sa z hľadiska krivky stratovosti od využiteľnosti javia vlastnosti všetkých algoritmov približne rovnaké. Zato z pohľadu pomeru odmietnutia a s tým úzko súvisiaci počet pripustených tokov do systému sa ako najlepší javí algoritmus Odmeraná suma.

Tieto výsledky ale nemožno považovať za všeobecné. Pri scenároch s iným druhom prevádzky možno rátať s inými výsledkami. To vyplýva napríklad aj zo simulácií pri internetovej prevádzke, kde sa algoritmus Odmeraná suma javil ako najhorší čo sa týka stratovosti, pomeru odmietnutia aj počtu pripustených tokov do systému. Zaujímavé výsledky ponúkol aj zdroj konštantnej prevádzky. Tu bolo vidno, že algoritmy Akceptačná oblasť – Dotyčnica na počiatku a Akceptačná oblasť – Dotyčnica vo vrchole vychádzajú z predpokladov On/Off prevádzkového generátora, takže pre tento druh zdroja sa ukazujú ako najmenej výhodné. Tu sa ako najlepší javil algoritmus Ekvivalentná šírka pásma, ktorý vykazoval veľmi uspokojivé výsledky aj pri predchádzajúcich prevádzkových generátoroch.

Každý algoritmus má svoje silnejšie aj slabšie stránky. Kde algoritmus Odmeraná suma síce nevychádza zo sofistikovaných matematických základov ako ostatné algoritmy (čo ho síce robí výpočtovo najjednoduchším), ale zato čerpá z flexibilného odhadu prevádzky, časové okno. Oproti tomu algoritmy Akceptačná oblasť – Dotyčnica na počiatku a Akceptačná oblasť – Dotyčnica vo vrchole podľa mňa trpia na jednoduchší odhad prevádzky napriek silným matematickým základom.

Z porovnávaných štyroch algoritmov sa najlepšie javil algoritmus Ekvivalentná šírka pásma, ktorý v sebe zahŕňa jednak flexibilný odhad prevádzky a takisto aj silný matematický základ. Takisto tento algoritmus vykazoval pri simuláciách najvyrovnanejšie a celkovo najlepšie výsledky. Určiť však Ekvivalentnú šírku pásma ako všeobecne najvhodnejší algoritmus z daných štyroch algoritmov nemusí byť definitívne. Na definitívnejšie určenie najlepšieho algoritmu by bolo treba vykonať ďalšie simulácie, napríklad s inými druhmi prevádzkových generátorov.

Alebo sa treba zamerať aj na iné parametre, ktoré ovplyvňujú dané algoritmy, ako oneskorenie, alebo kolísanie oneskorenia, poprípade sledovať správanie algoritmov pri použití viacerých druhov priorít prevádzky. Tieto alebo aj iné simulácie môžu už byť predmetom skúmania v ďalších článkoch. Je už teda priamo na prevádzkovateľovi siete, aký druh prevádzky je uňho najviac zastúpený a výber najvhodnejšieho algoritmu by mal voliť tak, aby sa čo najlepšie prispôsobil svojim požiadavkám.

5. Odkazy na literatúru

  1. Bohnert, T. M.: Admission Control for Packet Networks. Dostupné z:
    http://tmb.nginet.de/public/ac_lecture.pdf
  2. Jiang, Y. – Emstad, P. J. – Nicola, V. – Nevin, A.: Measurement-Based Admission Control: A Revisit. In: 17th Nordic Teletraffic Seminar. Fornebu: Nórsko, August 2004
  3. Jamin, S. – Shenker, S. J. – Danzig, P.B.: Comparison of Measurement-based Admission Control Algorithms for Controlled-Load Service. In: IEEE Infocom 1997. Kobe: Japonsko, Apríl 1997. S. 973-980. ISBN: 0-8186-7780-5
  4. Gibbens, R. J. – Kelly, F. P.: Measurement-based Connection Admission Control. In: 15th International Teletraffic Congress (ITC15). Washington: USA, Jún 1997
  5. Breslau,L. – Jamin, S. – Shenker, S.: Comments on the performance of measurement-based admission control algorithms. In: INFOCOM 2000. Tel Aviv: Izrael, Marec 2000. S. 1233-1242. ISBN: 0-7803-5880-5
Spoluautorom článku je Ing. Matej Kavacký, Phd., Ústav Telekomunikácii, Fakulta Elektrotechniky a Informatiky, Slovenská Technická Univerzita Ilkovičova 3, Bratislava 812 19

Napísať príspevok