Tabuľková metóda určovania koeficientov Mac-Laurinovho radu pre funkciu tangens

12. November, 2012, Autor článku: Milly Miron, Prírodné vedy
Ročník 5, číslo 11 This page as PDF Pridať príspevok

Príspevok popisuje princíp presnej a rýchlej metódy určovania koeficientov MacLaurinovho radu pre funkciu tangens pomocou číselnej tabuľky usporiadanej do riadkov a stĺpcov, a to podobným postupom, akým sa určujú koeficienty Binomického radu pomocou Pascalovho trojuholníka.

1. Úvod

Nech je daná reálna funkcia y = f(x) definovaná na množine reálnych čísel R . Nech táto funkcia má v bode x = 0 hodnoty y0 = f(0) . Nech v tomto bode x = 0 má daná funkcia y = f(x) aj hodnoty všetkých derivácií v označení:

y_0^{(1)}=f^{(1)}(0), \, y_0^{(2)}=f^{(2)}(0), \, y_0^{(3)}=f^{(3)}(0), \, \dots, \, y_0^{(n)}=f^{(n)}(0), \dots

Pre rozvoj funkcie y = f (x) do MacLaurinovho radu platí známy vzorec:

y=f(x)=f(0)+\frac{f^{(1)}(0)}{1!}x^1+\frac{f^{(2)}(0)}{2!}x^2+\dots=\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}

pričom:

y_0=y_0^{(0)}=f^{(0)}(0)=f(0), \, 0!=1, \, n=0,1,2,\dots

Rozvoj nami požadovanej funkcie y=tg(x) má podľa [2] tvar:

y=tg(x)=1.x^1+\frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 + \frac{62}{2835}x^9+\dots

V ďalšom zaveďme vyjadrenie 1. derivácie funkcie y = f(x) ako funkciu závisle premennej y v tvare: y^{(1)}=dy/dx=z(y), pričom pre funkciu y = f(x) sa budeme pridržiavať označenia: y^{(0)}= y=f(x), čo po formálnej stránke predstavuje deriváciu nultého rádu. Potom derivácie vyšších rádov y(1), y(2), y(3), … , y(n), … danej funkcie y = f(x) možno vyjadriť aj takto:

y^{(1)} = \frac{d}{dx}\left [ y^{(0)} \right ] = \frac{d}{dy}\left [ y^{(0)} \right ]\frac{dy}{dx} = \frac{dy}{dy} \frac{dy}{dx} = 1. z(y)

y^{(2)} = \frac{d}{dx}\left [ y^{(1)} \right ] = \frac{d}{dy}\left [ y^{(1)} \right ]\frac{dy}{dx} = \frac{d}{dy} \left [ y^{(1)} \right ] z(y)

…

y^{(n)} = \frac{d}{dx}\left [ y^{(n-1)} \right ] = \frac{d}{dy}\left [ y^{(n-1)} \right ]\frac{dy}{dx} = \frac{d}{dy} \left [ y^{(n-1)} \right ] z(y)

2. Popis metódy

Reálna funkcia y=tg(x) je periodická funkcia, ktorej jedna časť je definovaná v intervale -(π/2) < x < (π/2). Pre 1. deriváciu funkcie y=tg(x) platia vzťahy:

y^{(1)}=1/cos^2(x)=1+tg^2(y)=1+y^2=z(y)

V zmysle už spomenutého postupu vyjadrenia derivácie nultého rádu y(0) = y = f(x) a vyšších rádov y(1), y(2), y(3), … , y(n), … danej funkcie y = f(x) pomocou funkcie y(1) = dy/dx = z(y) možno pre funkciu y=tg(x) vypočítať jej vyššie derivácie celkom jednoduchým spôsobom:

y^{(0)} = f(x)=1.y

y^{(1)} = 1(1+y^2)=1+1.y^2

y^{(2)} = 2^1y(1+y^2)=2(y+y^3)

y^{(3)} = 2^1(1+3y^2)(1+y^2)=2(y+y^3)

y^{(4)} = 2^3(2y+3y^3)(1+y^2)=2^3(2y+5y^3+3y^5)

y^{(5)} = 2^3(2+15y^2+15y^4)(1+y^2)=2^3(2+17y^2+30y^4+15y^6)

y^{(6)} = 2^4(17y+60y^3+45y^5)(1+y^2)=2^4(17y+77y^3+105y^5+45y^7)

…

y^{(12)} = 2^{10}(21944y+302575y^3+140240y^5+3075930y^7+
+3513510y^9+2027025y^{11}+467775y^{13}

y^{(13)} = 2^{10}(21944+929569y^2+7919739y^4+28543515y^6+
+53153100y^8+53918865y^{10}+28378350y^{12}+6081075y^{14}

Všimnime si, že posledný koeficient polynómu y(n) pri mocnine yn+1 má hodnotu faktoriálu (n!). Pre overenie správnosti vypočítajme koeficienty polynómov y(9) a y(13) pri mocninách y9 a y13:

9! = 9.(2^3).7.(3.2).5.(2^2).3.2.1=[9.7.3.5.3.2^7]= 2835.2^7

13! = 13.(3.2^3).11.(5.2).[9!]=13.3.11.5.[9!].2^{1-}=6081075.2^{10}

Na základe vyjadrení derivácií nultého rádu a vyšších rádov y(0), y(1), y(2), y(3), … , y(n), … danej funkcie y = f(x) pomocou funkcie y(1) = dy/dx = z(y) zostavme pre funkciu y=tg(x) číselnú schému (tabuľku) koeficientov polynómov pri mocninách y0, y1, y2, y3, … , yn, … (usporiadame ich do stĺpcov), a to pre príslušné rády ich derivácií y(0), y(1), y(2), y(3), … , y(n), … (usporiadame ich do riadkov), pričom y(0)=y=f(x).

Tab. 1. Číselná tabuľka koeficientov polynómov y(n) pri ich mocninách y0, y1, y2, y3, …

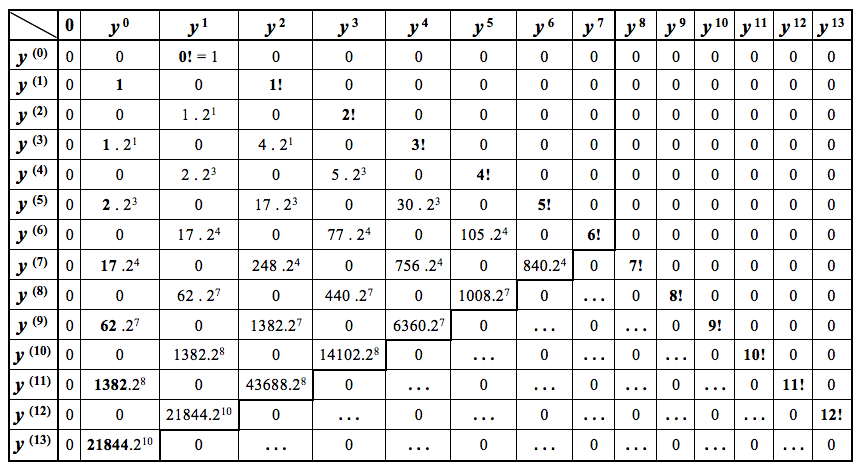
Analýzou takto získanej číselnej schémy možno zistiť, že v nej existujú isté zákonitosti, na základe ktorých možno určiť číselné hodnoty v dvoch za sebou nasledujúcich riadkoch, a to podobným postupom, akým sa určujú koeficienty Binomického radu pomocou známeho Pascalovho trojuholníka. Uveďme konkrétne príklady:

  • Konkrétne číslo 2, prislúchajúce riadku a stĺpcu [y(2), y1], možno určiť ako súčet dvoch čísel umiestnených nad riadkom y(2) po jeho oboch stranách (teda v riadku y(1)), vynásobených rádmi príslušných stĺpcov (teda rádmi stĺpcov y0, y2):

[y^{(2)},y^1]=0.[y^{(1)},y^1]+2.[y^{(1)},y^2] = 0.1+2.1!=2

  • Konkrétne číslo 2, prislúchajúce riadku a stĺpcu:

[y^{(3)},y^0]=0.[y^{(2)},0]+1.[y^{(2)},y^1] = 0+1.2=2

pričom stĺpec 0, (vľavo od stĺpca y0) má nulové hodnoty koeficientov.

  • Konkrétne číslo 6, prislúchajúce riadku a stĺpcu:

[y^{(3)},y^4]=3.[y^{(2)},y^3]+5.[y^{(2)},y^5] = 3.2!+5.0=3!=6

  • Konkrétne číslo 8, prislúchajúce riadku a stĺpcu:

[y^{(3)},y^2]=1.[y^{(2)},y^1]+3.[y^{(2)},y^3] = 1.2+3.2!=2+6=8

Ľahko sa možno presvedčiť, že horeuvedený algoritmus platí aj pre určovanie nulových hodnôt v riadkoch a stĺpcoch: [y(1), y1] , [y(2), y0], [y(2), y2] , [y(3), y1] , [y(3), y3] , … , atd.

Výhodou uvedeného algoritmu určovania koeficientov pri mocninách y0, y1, y2, y3, … , yn, … je skutočnosť, že pre určenie koeficientu, ktorý prislúcha riadku a stĺpcu [y(2n+1), y0] stačí poznať hodnoty koeficientov polynómov, ktoré prislúchajú riadku y(n). Tak napríklad pre určenie koeficientu v riadku a stĺpci: [y(13), y0] = 21844.28 stačí poznať koeficienty polynómov, ktoré prislúchajú riadku (polynómu) y(6):

y^{(6)}=2^4.(17y+77.y^3+105.y^5+45.y^7)

Koeficient y(13)(0)/13! MacLaurinovho radu pri mocnine x13 možno určiť aj z polynómu y(13)=210.21844.y0 + … + 13!.y14 ako podiel koeficientu s hodnotou y(13)=210.21844 pri mocnine y0 a koeficientu s hodnotou 13! pri mocnine y14. V obecnom prípade možno vysloviť tvrdenie, že hodnota koeficientu y(2n+1)(0)/(2n+1)! pri mocnine x(2n+1) MacLaurinovho radu pre funkciu y=tg(x) je určená podielom koeficientu pri ráde y0 a príslušnej hodnote faktoriálu [(2n +1)!]. Na základe uvedeného MacLaurinov rad funkcie y=tg(x) má tvar:

y=tg(x)=1.x^1+\frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 + \frac{62}{2835}x^9+\frac{1382}{155925}x^{11}+\dots

3. Záver

Účelom predkladaného príspevku bolo prezentovať doposiaľ novú metódu presného a rýchleho postupu určovania koeficientov MacLaurinovho radu pre funkciu y=tg(x). Spomínaná tabuľková metóda umožňuje bez zložitých výpočtov určovať jeho koeficienty na základe veľmi jednoduchého algoritmu zostaveného do číselnej schémy v podobe tabuľky, a to až do vysokých rádov mocnín xn. Pripomíname však, že uvedená metóda nemá širšie využitie pre obecné funkcie y=f(x).

Literatúra

  1. Grega, A.– Kluvanec, D.–Rajčan, E.: Matematika pre fyzikov. SPN, Bratislava 1974.
  2. Bronštejn, I.N.– Semenďajev, K.A: Príručka matematiky pre inžinierov a pre študujúcich (preklad 8. ruského vydania – 3. slovenské vydanie), SVTL, Bratislava 1964.
  3. Göhler, W.–Ralle, B.: Lexikón vyššej matematiky – vzorce. ALFA, Bratislava 1964.

Napísať príspevok