Mechanical vibration – Chapter 2: Free vibration of undamped 1-DOF linear system
23. November, 2012, Autor článku: Goga Vladimír, Elektrotechnika
Ročník 5, číslo 11  Pridať príspevok
Pridať príspevok
![]() This chapter is focused on the vibration of 1-DOF undamped linear system from kinematics point of view. Just kinematic quatities as displacement, velocity and acceleration of mass will be analyzed. Force effects on the mass during vibration are problem of dynamics and it will be discussed in the next part of this chapter.
This chapter is focused on the vibration of 1-DOF undamped linear system from kinematics point of view. Just kinematic quatities as displacement, velocity and acceleration of mass will be analyzed. Force effects on the mass during vibration are problem of dynamics and it will be discussed in the next part of this chapter.
Let’s consider mass-spring oscillator shown in Fig. 1 which represents undamped 1-DOF vibration system (1-DOF means that mass can move only in one direction, in this case it is y coordinate). When the mass is displaced from its equilibrium or it is forced by initial velocity the mass starts oscillate about its equilibrium position due restoring linear elastic force in spring. Displacement response (Fig. 1) shows that the motion of oscillator is periodic and it is apparent that it can be described by sine or cosine harmonic function with independent parameter – time t.
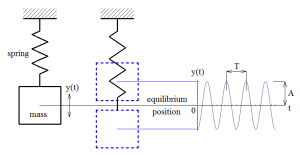
Fig. 1 Vibration of mass-spring oscillator and its displacement response.
Harmonic functions sine or cosine can be explain by kinematics of rotational motion. Circular plate rotates about its center with constant angular velocity ω. Let’s analyze movement of point M on the plate. This point moves along the circumference of a circle. Projection of point shadow on vertical wall shows that point makes translational periodic motion. When the mass-spring oscillator with specific parameters is placed next the rotating plate, projections of point M and mass of oscillator are alignment. Point M makes the same motion like oscillator in vertical direction.
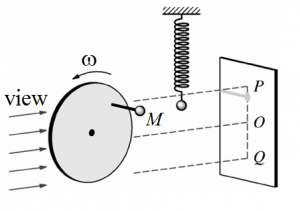
Fig. 2 Similarity of motions: rotation motion and vertical motion of oscillator [1].
Point coordinates in x and y directions are (Fig. 3):
where ϕ is angle between vector r and x axis (Fig. 2). Vector r determines the position of point M. For uniform circular motion angle ϕ is defined by equation:
and coordinates of point M are (r=|r|):
We are interested in only y direction of point position. Maximum displacement ym is given by radius r and is called amplitude A:
then:
Constant angular velocity ω (rad.s-1) represents change of angle ϕ (unit: rad) in time 1 second. Duration of one turn (2π rad) is called period T (unit: second) and it can be calculated from angular velocity:
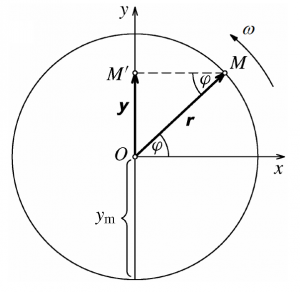
Fig. 3 Point position on circle path [1].
For vibration systems the angular velocity ω is called angular frequency. In practice the ordinary frequency f (or just a frequency) is commonly use. This frequency represents number of oscillations (turns) in 1 second. Physical unit is hertz: Hz or s-1. Relationships between ω, T and f are:
Velocity vector v of point M is tangent to point’s trajectory. Speed value is v=|v| and can be calculated by equation: v=ωr. Velocity component in y direction is (Fig. 4):
where ωr is amplitude of velocity. Tangent acceleration is zero because angular velocity is constant. Only centripetal acceleration a0 acting on point M. Centripetal acceleration value is defined:
Centripetal acceleration component in y direction is (Fig. 4):
where ω2r is amplitude of acceleration. We can see that the direction of acceleration is always opposite to displacement and velocity.
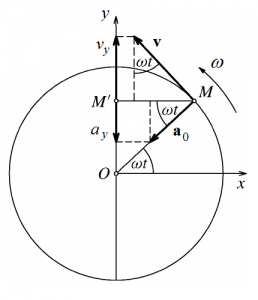
Fig. 4 Velocity and acceleration of circular motion [1].
The same equations for velocity and acceleration we get from physics. Time derivation of displacement y is velocity vy:
and time derivation of velocity vy is acceleration ay:
For 1-DOF system we can omit the index “y” for velocity and acceleration because it is clear that these quantities belong for y DOF. In general, oscillation motion of undamped 1-DOF linear system is described by harmonic functions:
| Quantity | Equation | Amplitude |
|---|---|---|
| displacement | ||
| velocity | ||
| acceleration |
These equations for rotational motion (displacement, velocity and acceleration) are the same for undamped mass-spring oscillator. But the mass-spring system is characterized by physical parameters: mass weight m and spring stiffness k. We must apply dynamics laws to include these parameters to the equations for mass-spring oscillator – it is a task of dynamics.
Appendix
Fig. 5 shows time diagrams of kinematic quantities for vibration system with displacement function:
Angular frequency:
Period (duration of one oscillation):
Frequency (number of oscillations in 1 second):
| Quantity | Angular frequency [rad.s-1] | Amplitude |
|---|---|---|
| displacement | 4π | 0,01 [m] |
| velocity | 4π | 4π·0,01 = 0,1256 [m.s-1] |
| acceleration | 4π | (4π)2·0,01 = 1,5775 [m.s-2] |
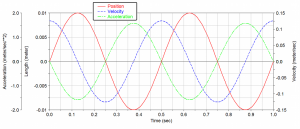
Fig. 5 Time diagrams of kinematic quantities.
References

