Virtuálne procesy v Matlabe
30. Január, 2013, Autor článku: Gvoth Juraj, Elektrotechnika, Informačné technológie, Študentské práce
Ročník 6, číslo 1 
Pridať príspevok
V praxi sa často stretávame s nedostatkom reálnych modelov na výučbové procesy. Tento fakt vedie k vytváraniu buď samotných reálnych modelov, ktoré prinášajú do celého výučbového procesu nároky na hardvérové vybavenie, alebo virtuálnych modelov, ktoré ale neobsahujú všetky komplexné štruktúry reálneho systému.
Jednou z možností vytvárania takýchto virtuálnych modelov je práve jazyk VRML [1]. Ten samotný však na animáciu scény nepostačuje, pretože je potrebné tejto scéne meniť vlastnosti objektov výstupmi namodelovaného procesu. Na našej fakulte prebieha výučba s využitím programu Matlab, a preto budeme vytvárať model quad-koptéry v prostredí Matlab-Simulink [2] a pomocou toolboxu S3D [3] budeme animovať VRML scénu.
Quad-koptéra
Quad-koptéra je zariadenie podobné helikoptére avšak na rozdiel od helikoptéry používa štyri rotory natočené nahor rozložené v rohoch pomyselného štvorca. Celé ovládanie quad-koptéry teda spočíva v zmene uhlových rýchlostí jednotlivých rotorov čím zabezpečíme naklonenie zariadenia a následne jeho zmenu pozície v priestore. Takéto zariadenie sa radí do kategórie UAV (unmanned aerial vehicles) a tomu zodpovedá aj jeho použitie, napr. v pátracích akciách, inšpekciách na stavbe a pod.
Matematický model quad-koptéry
Matematický model bude vo výsledku opisovať fyziku quad-koptéry len v zjednodušenom ponímaní. Ak by sme chceli modelovať všetky vplyvy na správanie sa quad-koptéry počas letu, model by sa značne skomplikoval a sťažilo by to samotnú simuláciu, ktorá by sa tak mohla stať náročná na výpočet. Rovnice a Obr. 1 boli prebrané z [3]. Na Obr. 1 vidíme základnú štruktúru quad-koptéry, svetový súradnicový systém, súradnicový systém samotnej quad-koptéry, uhlové rýchlosti motorov a momenty a sily nimi vytvorené.
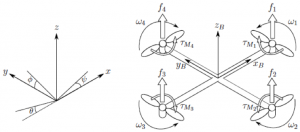
Obr. 1 Základná štruktúra quad-koptéry
Pozíciu quad-koptéry voči svetovému súradnicovému systému bude opisovať vektor ξ a uhly natočenia zas vektor η.
![\xi = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]; \; \eta = \left[ \begin{array}{c} \phi \\ \theta \\ \psi \end{array} \right]; \; \nu = \left[ \begin{array}{c} p \\ q \\ r \end{array} \right]](http://s0.wp.com/latex.php?latex=%5Cxi+%3D++%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+x+%5C%5C+y+%5C%5C+z+%5Cend%7Barray%7D+%5Cright%5D%3B+%5C%3B+%5Ceta+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cphi+%5C%5C+%5Ctheta+%5C%5C+%5Cpsi+%5Cend%7Barray%7D+%5Cright%5D%3B+%5C%3B+%5Cnu+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+p+%5C%5C+q+%5C%5C+r+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "\xi = \left[ \begin{array}{c} x \\ y \\ z \end{array} \right]; \; \eta = \left[ \begin{array}{c} \phi \\ \theta \\ \psi \end{array} \right]; \; \nu = \left[ \begin{array}{c} p \\ q \\ r \end{array} \right]") |
(1) |
Natočenie quad-koptéry vo svetovom súradnicovom systéme popisujeme prostredníctvom Eulerových uhlov, kde ϕ je tzv. „roll“ čo predstavuje uhol otáčania okolo osi x, θ zasa „pitch“ čo je uhol stúpania (natočenie okolo osi y) a ψ ako uhol vytočenia okolo osi z, tzv. „yaw“. Budeme taktiež používať vektor ν, ktorý bude obsahovať jednotlivé uhlové rýchlosti, ale vzhľadom na samotné telo quad-koptéry. Rotačná matica zo súradnicového systému quad-koptéry do svetového súradnicového systému.
![R = \left[ \begin{array}{ccc} C_{\psi}C_{\theta} & C_{\psi}S_{\theta}S_{\phi} - S_{\psi}C_{\phi} & C_{\psi}S_{\theta}C_{\phi} + S_{\psi}S_{\phi} \\ S_{\psi}C_{\theta} & S_{\psi}S_{\theta}S_{\phi} + C_{\psi}C_{\phi} & S_{\psi}S_{\theta}C_{\phi} - C_{\psi}S_{\phi} \\ -S_{\theta} & C_{\theta}S_{\phi} & C_{\theta}C_{\phi} \end{array} \right]](http://s0.wp.com/latex.php?latex=R+%3D++%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+C_%7B%5Cpsi%7DC_%7B%5Ctheta%7D+%26+C_%7B%5Cpsi%7DS_%7B%5Ctheta%7DS_%7B%5Cphi%7D+-+S_%7B%5Cpsi%7DC_%7B%5Cphi%7D+%26+C_%7B%5Cpsi%7DS_%7B%5Ctheta%7DC_%7B%5Cphi%7D+%2B+S_%7B%5Cpsi%7DS_%7B%5Cphi%7D+%5C%5C+S_%7B%5Cpsi%7DC_%7B%5Ctheta%7D+%26+S_%7B%5Cpsi%7DS_%7B%5Ctheta%7DS_%7B%5Cphi%7D+%2B+C_%7B%5Cpsi%7DC_%7B%5Cphi%7D+%26+S_%7B%5Cpsi%7DS_%7B%5Ctheta%7DC_%7B%5Cphi%7D+-+C_%7B%5Cpsi%7DS_%7B%5Cphi%7D+%5C%5C+-S_%7B%5Ctheta%7D+%26+C_%7B%5Ctheta%7DS_%7B%5Cphi%7D+%26+C_%7B%5Ctheta%7DC_%7B%5Cphi%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "R = \left[ \begin{array}{ccc} C_{\psi}C_{\theta} & C_{\psi}S_{\theta}S_{\phi} - S_{\psi}C_{\phi} & C_{\psi}S_{\theta}C_{\phi} + S_{\psi}S_{\phi} \\ S_{\psi}C_{\theta} & S_{\psi}S_{\theta}S_{\phi} + C_{\psi}C_{\phi} & S_{\psi}S_{\theta}C_{\phi} - C_{\psi}S_{\phi} \\ -S_{\theta} & C_{\theta}S_{\phi} & C_{\theta}C_{\phi} \end{array} \right]") |
(2) |
Kde Sx=sin(x) a podobne. Kedže je rotačná matica R ortogonálna, platí R-1=RT čo je rotačná matica zo svetového súradnicového systému do súradnicového systému quad-koptéry. Transformačná matica Wη na prepočet uhlových rýchlostí zo svetového súradnicového systému do súradnicového systému quad-koptéry a Wη-1 opačne.
![\nu = W_{\eta} \dot{\eta}, \; \left[ \begin{array}{c} p \\ q \\ r \end{array} \right]=\left[ \begin{array}{ccc} 1 & 0 & -S_{\theta} \\ 0 & C_{\phi} & C_{theta}S_{\phi} \\ 0 & -S_{\phi} & C_{theta}C_{\phi} \end{array} \right] \left[ \begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array} \right]](http://s0.wp.com/latex.php?latex=%5Cnu+%3D+W_%7B%5Ceta%7D+%5Cdot%7B%5Ceta%7D%2C+%5C%3B+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+p+%5C%5C+q+%5C%5C+r+%5Cend%7Barray%7D+%5Cright%5D%3D%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+1+%26+0+%26+-S_%7B%5Ctheta%7D+%5C%5C+0+%26+C_%7B%5Cphi%7D+%26+C_%7Btheta%7DS_%7B%5Cphi%7D+%5C%5C+0+%26+-S_%7B%5Cphi%7D+%26+C_%7Btheta%7DC_%7B%5Cphi%7D+%5Cend%7Barray%7D+%5Cright%5D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cdot%7B%5Cphi%7D+%5C%5C+%5Cdot%7B%5Ctheta%7D+%5C%5C+%5Cdot%7B%5Cpsi%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "\nu = W_{\eta} \dot{\eta}, \; \left[ \begin{array}{c} p \\ q \\ r \end{array} \right]=\left[ \begin{array}{ccc} 1 & 0 & -S_{\theta} \\ 0 & C_{\phi} & C_{theta}S_{\phi} \\ 0 & -S_{\phi} & C_{theta}C_{\phi} \end{array} \right] \left[ \begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array} \right]") |
(3) |
![\dot{\eta} = W_{\eta}^{-1} \dot{\nu}, \; \left[ \begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array} \right]=\left[ \begin{array}{ccc} 1 & S_{\phi}T_{\theta} & C_{\phi}T_{\theta} \\ 0 & C_{\phi} & -S_{\phi} \\ 0 & S_{\phi}/C_{\theta} & C_{\phi}/C_{\theta} \end{array} \right] \left[ \begin{array}{c} p \\ q \\ r \end{array} \right]](http://s0.wp.com/latex.php?latex=%5Cdot%7B%5Ceta%7D+%3D+W_%7B%5Ceta%7D%5E%7B-1%7D+%5Cdot%7B%5Cnu%7D%2C+%5C%3B+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cdot%7B%5Cphi%7D+%5C%5C+%5Cdot%7B%5Ctheta%7D+%5C%5C+%5Cdot%7B%5Cpsi%7D+%5Cend%7Barray%7D+%5Cright%5D%3D%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+1+%26+S_%7B%5Cphi%7DT_%7B%5Ctheta%7D+%26+C_%7B%5Cphi%7DT_%7B%5Ctheta%7D+%5C%5C+0+%26+C_%7B%5Cphi%7D+%26+-S_%7B%5Cphi%7D+%5C%5C+0+%26+S_%7B%5Cphi%7D%2FC_%7B%5Ctheta%7D+%26+C_%7B%5Cphi%7D%2FC_%7B%5Ctheta%7D+%5Cend%7Barray%7D+%5Cright%5D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+p+%5C%5C+q+%5C%5C+r+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "\dot{\eta} = W_{\eta}^{-1} \dot{\nu}, \; \left[ \begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array} \right]=\left[ \begin{array}{ccc} 1 & S_{\phi}T_{\theta} & C_{\phi}T_{\theta} \\ 0 & C_{\phi} & -S_{\phi} \\ 0 & S_{\phi}/C_{\theta} & C_{\phi}/C_{\theta} \end{array} \right] \left[ \begin{array}{c} p \\ q \\ r \end{array} \right]") |
(4) |
Keďže sa predpokladá symetrické rozloženie ramien quad-koptéry v osiach x a y, matica zotrvačnosti bude diagonálna matica I kde Ixx = Iyy.
![I=\left[ \begin{array}{ccc} I_{xx} & 0 & 0 \\ 0 & I_{yy} & 0 \\ 0 & 0 & I_{zz} \end{array} \right]](http://s0.wp.com/latex.php?latex=I%3D%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+I_%7Bxx%7D+%26+0+%26+0+%5C%5C+0+%26+I_%7Byy%7D+%26+0+%5C%5C+0+%26+0+%26+I_%7Bzz%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "I=\left[ \begin{array}{ccc} I_{xx} & 0 & 0 \\ 0 & I_{yy} & 0 \\ 0 & 0 & I_{zz} \end{array} \right]") |
(5) |
Každý z motorov vytvára silu fi a krútiaci moment τMi okolo svojej osi.
 |
(6) |
Hodnota 
![T=\sum_{i=1}^4 f_i=k \sum_{i=1}^4 \omega_i^2, \; T_B=\left[ \begin{array}{c} 0 \\ 0 \\ T \end{array} \right]](http://s0.wp.com/latex.php?latex=T%3D%5Csum_%7Bi%3D1%7D%5E4+f_i%3Dk+%5Csum_%7Bi%3D1%7D%5E4+%5Comega_i%5E2%2C+%5C%3B+T_B%3D%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+0+%5C%5C+0+%5C%5C+T+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "T=\sum_{i=1}^4 f_i=k \sum_{i=1}^4 \omega_i^2, \; T_B=\left[ \begin{array}{c} 0 \\ 0 \\ T \end{array} \right]") |
(7) |
Vektor pre výsledný krútiaci moment sa skladá z krútiacich momentov, ktorých smery zodpovedajú smerom osí súradnicového systému quad-koptéry,
![\tau_B=\left[ \begin{array}{c} \tau_{\phi} \\ \tau_{\theta} \\ \tau_{\psi} \end{array} \right] = \left[ \begin{array}{c} lk(-\omega_2^2+\omega_4^2) \\ lk(-\omega_1^2+\omega_3^2) \\ \sum_{i=1}^4 \tau_{Mi} \end{array} \right]](http://s0.wp.com/latex.php?latex=%5Ctau_B%3D%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Ctau_%7B%5Cphi%7D+%5C%5C+%5Ctau_%7B%5Ctheta%7D+%5C%5C+%5Ctau_%7B%5Cpsi%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+lk%28-%5Comega_2%5E2%2B%5Comega_4%5E2%29+%5C%5C+lk%28-%5Comega_1%5E2%2B%5Comega_3%5E2%29+%5C%5C+%5Csum_%7Bi%3D1%7D%5E4+%5Ctau_%7BMi%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "\tau_B=\left[ \begin{array}{c} \tau_{\phi} \\ \tau_{\theta} \\ \tau_{\psi} \end{array} \right] = \left[ \begin{array}{c} lk(-\omega_2^2+\omega_4^2) \\ lk(-\omega_1^2+\omega_3^2) \\ \sum_{i=1}^4 \tau_{Mi} \end{array} \right]") |
(8) |
kde l je vzdialenosť osi motora od ťažiska quad-koptéry. Keďže je quad-koptéra tuhé teleso, použijeme Newton-Eulerove rovnice na opis jej dynamiky. Ako prvé pristúpime ku rovniciam opisujúcim aktuálnu polohu telesa vo svetovom súradnicovom systéme. V rovnici (9) je zapísaná podmienka rovnovážneho stavu v súradnicovom systéme quad-koptéry, kde sila potrebná na zrýchlenie hmotnosti m a odstredivá sila ν×(mVB) sa musia rovnať tiažovej sile RTG a ťahu rotorov TB.
 |
(9) |
Nakoľko vzhľadom na svetový súradnicový systém sa odstredivá sila nuluje, tak vplyv na zrýchlenie quad-koptéry má iba tiažová sila a veľkosť sily ťahu vyvolaného rotormi. Pretože ale potrebujeme rovnicu polohy vzhľadom na svetový súradnicový systém, je potrebné prenásobiť rovnicu rotačnou maticou R z čoho dostaneme rovnicu (10).
 |
(10) |
Po dosadení a úprave dostávame stavový opis (11), ktorý obsahuje prvé pohybové rovnice quad-koptéry pre jednotlivé osi svetového súradnicového systému.
![\left[ \begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{array} \right] = -g \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] + \frac{T}{m} \left[ \begin{array}{c} C_{\psi}S_{\theta}C_{phi} + S_{\psi}S_{phi} \\ S_{\psi}S_{\theta}C_{phi} - C_{\psi}S_{phi} \\ C_{\theta}C_{phi} \end{array} \right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cddot%7Bx%7D+%5C%5C+%5Cddot%7By%7D+%5C%5C+%5Cddot%7Bz%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+-g+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+0+%5C%5C+0+%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D+%2B+%5Cfrac%7BT%7D%7Bm%7D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+C_%7B%5Cpsi%7DS_%7B%5Ctheta%7DC_%7Bphi%7D+%2B+S_%7B%5Cpsi%7DS_%7Bphi%7D+%5C%5C+S_%7B%5Cpsi%7DS_%7B%5Ctheta%7DC_%7Bphi%7D+-+C_%7B%5Cpsi%7DS_%7Bphi%7D+%5C%5C+C_%7B%5Ctheta%7DC_%7Bphi%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "\left[ \begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{array} \right] = -g \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] + \frac{T}{m} \left[ \begin{array}{c} C_{\psi}S_{\theta}C_{phi} + S_{\psi}S_{phi} \\ S_{\psi}S_{\theta}C_{phi} - C_{\psi}S_{phi} \\ C_{\theta}C_{phi} \end{array} \right]") |
(11) |
V súradnicovom systéme quad-koptéry tiež platí rovnica (12), kde uhlové zrýchlenie zotrvačnosti 
 |
![\dot{\nu} = I^{-1} \left ( - \left[ \begin{array}{c} p \\ q \\ r \end{array} \right] \times \left[ \begin{array}{c} I_{xx}p \\ I_{yy}q \\ I_{zz}r \end{array} \right] - I_r \left[ \begin{array}{c} p \\ q \\ r \end{array} \right] \times \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] \omega_{\Gamma} + \tau \right ) \left[ \begin{array}{c} \dot{p} \\ \dot{q} \\ \dot{r} \end{array} \right] =](http://s0.wp.com/latex.php?latex=%5Cdot%7B%5Cnu%7D+%3D+I%5E%7B-1%7D+%5Cleft+%28+-+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+p+%5C%5C+q+%5C%5C+r+%5Cend%7Barray%7D+%5Cright%5D+%5Ctimes+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+I_%7Bxx%7Dp+%5C%5C+I_%7Byy%7Dq+%5C%5C+I_%7Bzz%7Dr+%5Cend%7Barray%7D+%5Cright%5D+-+I_r+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+p+%5C%5C+q+%5C%5C+r+%5Cend%7Barray%7D+%5Cright%5D+%5Ctimes+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+0+%5C%5C+0+%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D+%5Comega_%7B%5CGamma%7D+%2B+%5Ctau+%5Cright+%29+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cdot%7Bp%7D+%5C%5C+%5Cdot%7Bq%7D+%5C%5C+%5Cdot%7Br%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+&bg=ffffff&fg=000000&s=0 "\dot{\nu} = I^{-1} \left ( - \left[ \begin{array}{c} p \\ q \\ r \end{array} \right] \times \left[ \begin{array}{c} I_{xx}p \\ I_{yy}q \\ I_{zz}r \end{array} \right] - I_r \left[ \begin{array}{c} p \\ q \\ r \end{array} \right] \times \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] \omega_{\Gamma} + \tau \right ) \left[ \begin{array}{c} \dot{p} \\ \dot{q} \\ \dot{r} \end{array} \right] =") |
![\left[ \begin{array}{c} (I_{yy}-I_{zz})qr/I_{xx} \\ (I_{zz}-I_{xx})pr/I_{yy} \\ (I_{xx}-I_{yy})pq/I_{zz} \end{array} \right] -I_r \left[ \begin{array}{c} q/I_{xx} \\ -p/I_{yy} \\ 0 \end{array} \right] \omega_{\Gamma} + \left[ \begin{array}{c} \tau_{\phi}/I_{xx} \\ \tau_{\theta}/I_{yy} \\ \tau_{\psi}/I_{zz} \end{array} \right]](http://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%28I_%7Byy%7D-I_%7Bzz%7D%29qr%2FI_%7Bxx%7D+%5C%5C+%28I_%7Bzz%7D-I_%7Bxx%7D%29pr%2FI_%7Byy%7D+%5C%5C+%28I_%7Bxx%7D-I_%7Byy%7D%29pq%2FI_%7Bzz%7D+%5Cend%7Barray%7D+%5Cright%5D+-I_r+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+q%2FI_%7Bxx%7D+%5C%5C+-p%2FI_%7Byy%7D+%5C%5C+0+%5Cend%7Barray%7D+%5Cright%5D+%5Comega_%7B%5CGamma%7D+%2B+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Ctau_%7B%5Cphi%7D%2FI_%7Bxx%7D+%5C%5C+%5Ctau_%7B%5Ctheta%7D%2FI_%7Byy%7D+%5C%5C+%5Ctau_%7B%5Cpsi%7D%2FI_%7Bzz%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "\left[ \begin{array}{c} (I_{yy}-I_{zz})qr/I_{xx} \\ (I_{zz}-I_{xx})pr/I_{yy} \\ (I_{xx}-I_{yy})pq/I_{zz} \end{array} \right] -I_r \left[ \begin{array}{c} q/I_{xx} \\ -p/I_{yy} \\ 0 \end{array} \right] \omega_{\Gamma} + \left[ \begin{array}{c} \tau_{\phi}/I_{xx} \\ \tau_{\theta}/I_{yy} \\ \tau_{\psi}/I_{zz} \end{array} \right]") |
(12) |
Platí ωΓ=ω1-ω2+ω3-ω4. Aby sme ale mohli pracovať s uhlami natočenia quad-koptéry vo svetovom súradnicovom systéme, je potrebné použiť transformačnú rovnicu (4). Rovnice, ktorými sme doteraz opísali dynamiku quad-koptéry poskytujú len zjednodušenie komplexných dynamických väzieb procesu. Aby sme zabezpečili reálnejší model, pridáme do rovnice (11) člen reprezentujúci silu, ktorá vzniká pôsobením odporu vzduchu. Jedná sa o vektorový súčin diagonálnej matice s koeficientmi odporu vzduchu v jednotlivých osiach a lineárnych rýchlostí kvadkoptéry v svetovom súradnicovom systéme.
![\left[ \begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{array} \right] = -g \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] + \frac{T}{m} \left[ \begin{array}{c} C_{\psi}S_{\theta}C_{phi} + S_{\psi}S_{phi} \\ S_{\psi}S_{\theta}C_{phi} - C_{\psi}S_{phi} \\ C_{\theta}C_{phi} \end{array} \right] -](http://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cddot%7Bx%7D+%5C%5C+%5Cddot%7By%7D+%5C%5C+%5Cddot%7Bz%7D+%5Cend%7Barray%7D+%5Cright%5D+%3D+-g+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+0+%5C%5C+0+%5C%5C+1+%5Cend%7Barray%7D+%5Cright%5D+%2B+%5Cfrac%7BT%7D%7Bm%7D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+C_%7B%5Cpsi%7DS_%7B%5Ctheta%7DC_%7Bphi%7D+%2B+S_%7B%5Cpsi%7DS_%7Bphi%7D+%5C%5C+S_%7B%5Cpsi%7DS_%7B%5Ctheta%7DC_%7Bphi%7D+-+C_%7B%5Cpsi%7DS_%7Bphi%7D+%5C%5C+C_%7B%5Ctheta%7DC_%7Bphi%7D+%5Cend%7Barray%7D+%5Cright%5D+-+&bg=ffffff&fg=000000&s=0 "\left[ \begin{array}{c} \ddot{x} \\ \ddot{y} \\ \ddot{z} \end{array} \right] = -g \left[ \begin{array}{c} 0 \\ 0 \\ 1 \end{array} \right] + \frac{T}{m} \left[ \begin{array}{c} C_{\psi}S_{\theta}C_{phi} + S_{\psi}S_{phi} \\ S_{\psi}S_{\theta}C_{phi} - C_{\psi}S_{phi} \\ C_{\theta}C_{phi} \end{array} \right] -") |
![-\frac{1}{m} \left[ \begin{array}{ccc} A_x & 0 & 0 \\ 0 & A_y & 0 \\ 0 & 0 & A_z \end{array} \right] \left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{z} \end{array} \right]](http://s0.wp.com/latex.php?latex=-%5Cfrac%7B1%7D%7Bm%7D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bccc%7D+A_x+%26+0+%26+0+%5C%5C+0+%26+A_y+%26++0+%5C%5C+0+%26+0+%26+A_z+%5Cend%7Barray%7D+%5Cright%5D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bc%7D+%5Cdot%7Bx%7D+%5C%5C+%5Cdot%7By%7D+%5C%5C+%5Cdot%7Bz%7D+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=000000&s=0 "-\frac{1}{m} \left[ \begin{array}{ccc} A_x & 0 & 0 \\ 0 & A_y & 0 \\ 0 & 0 & A_z \end{array} \right] \left[ \begin{array}{c} \dot{x} \\ \dot{y} \\ \dot{z} \end{array} \right]") |
(13) |
Podobným spôsobom možné pridať ešte ďalšie aerodynamické vplyvy, ako napríklad vibrácia listov vrtule, alebo prúdenie vzduchu. No to by už malo za následok značne zložitejší matematický model.
Virtuálny model
Pri tvorbe modelu bolo potrebné najprv vopred premyslieť štruktúru „funkčných objektov“. Ako už bolo v odseku o VRML spomenuté, potomok mení svoje vlastnosti vždy vzhľadom na rodiča čo bude stavebným kameňom pri návrhu štruktúry modelu. Za najdôležitejšie sme si zoberali polohu quad-koptéry. Túto vlastnosť bude teda animovať funkčný objekt s názvom „core“. Natáčanie jedného objektu vo viac ako jednom smere je komplikované, a preto radšej vytvoríme tri funkčné objekty s názvami „rot_x“, „rot_y“, „rot_z“. Tieto objekty budú slúžiť na animáciu natočenia quad-koptéry okolo jednotlivých osí.
Aby bolo zreteľne vidno zmeny polohy a natočenia vytvorili sme tiež objekty znázorňujúce svetový súradnicový systém s názvami „world_coord_zero“, „w_axis_x“, „w_axis_y“, „w_axis_z“. Taktiež sme vytvorili objekty „b_axis_x“, „b_axis_y“, „b_axis_z“. Tieto budú pevne späté so samotným telom quadkoptéry ako je to na Obr. 1. Takže budú nasledovať ako zmenu polohy quad-koptéry tak aj je naklonenie okolo jednotlivých osí. Pre kompletnosť ešte vytvoríme objekty „axis_x“, „axis_y“, „axis_z“. Objekty budú síce nasledovať quad-koptéru v zmysle jej polohy, ale stále budú rovnobežné s objektmi, ktoré tvoria osi svetového súradnicového systém.
Samotné telo quad-koptéry budeme považovať za jeden celistvý objekt s názvom „quad_body“ s výnimkou objektov „r_1“, „r_2“, „r_3“, „r_4“, čo budú objekty slúžiace na animáciu rotorov. Posledné vytvoríme rotory samotné pomocou objektov „rot_1“, „rot_2“, „rot_3“, „rot_4“. Pre vytvorenie tela quad-koptéry sme si za vzor zobrali quad-koptéru na Obr. 2.
Obr. 2 Vzor pre VRML model tela quad-koptéry
Tiež bolo potrebné vytvoriť priestor, v ktorom sa bude quad-koptére umožnené pohybovať. Ten tvorí miestnosť s rozmermi 5x5x2m. Presný stred miestnosti je považovaný za bod [0,0,0] a teda najnižší bod v miestnosti môže nadobudnúť hodnotu v osi z -1 a najvyšší 1. Do miestnosti boli taktiež umiestnené tri prekážky s rôznymi rozmermi. Všetky objekty sa dotýkajú podstavou podlahy. Prvá prekážka žltej farby a tvaru kocky s dĺžkou hrany 0.6m a jej stred je na pozícii [0,1.5] (x,y), druhá zelenej farby s rozmermi 1.5×1.5×0.4m (x,y,z) a jej stred na pozícii [-1,-1.5] (x,y) a posledná ružovej farby s rozmermi 0.4×0.4x2m (x,y,z) a jej stred na pozícii [1.5,-1] (x,y).
Steny a strop miestnosti majú nastavenú 50% transparentosť, aby bolo možné sledovať pohyb quad-koptéry a zároveň sme mali vizuálnu predstavu o vymedzenom priestore. Keďže je pre nás najzaujímavejšia hierarchia objektov tvoriacich quad-koptéru, podrobnejšie si rozoberieme iba túto časť celkovej VRML scény. Ako už bolo vyššie spomenuté, najvyšším rodičom v tejto časti VRML scény bude funkčný objekt „core“, ten bude mať ako potomkov funkčné objekty „rot_x“, „rot_y“ a „rot_z“, ktoré budú aj medzi sebou postupne, v poradí ako boli napísané, vo vzťahu rodič – potomok. Funkčnému objektu „rot_z“ bude už potomkom priamo telo quad-koptéry vytvorené sústavou rôznych geometrických objektov. Telo quad-koptéry však ešte má ako svojich potomkov štyri funkčné objekty, ktoré budú animovať otáčanie jednotlivých rotorov. Týmto funkčným objektom samozrejme ešte boli vytvorené vizuálne zobrazenia rotorov samotných.
Aby sme zabezpečili detekciu kolízie quad-koptéry s prekážkami, alebo samotnými stenami, podlahou či stropom miestnosti, bolo potrebné vytvoriť dvadsaťšesť tzv. kolíznych bodov a rozmiestniť ich vhodne okolo tela quad-koptéry. Tieto body sú potomkami funkčného objektu „rot_z“. Na Obr. 3 máme blízky pohľad na výsledný tvar tela quad-koptéry a zároveň aj rozmiestnenie kolíznych bodov a na Obr. 4 vidíme výslednú VRML scénu.
Obr. 3 Pohľad na telo quad-koptéry a rozmiestnenie kolíznych bodov
Obr. 4 Výsledná VRML scéna
Nakoľko letový priestor quad-koptéry obsahuje prekážky a z jedného pohľadu by sme nemali dostatočný prehľad o lete quad-koptéry. Boli ešte vytvorené štyri View-pointy, kde nám z každý z nich ponúka pohľad na celkovú scénu z jedného zo štyroch rohov miestnosti. Tiež boli pridané tri View-pointy späté s telom Quad-koptéry. Prvý je pohľad spoza tretieho rotoru a nasleduje celkové natočenie quad-koptéry, druhý je pohľad z perspektívy zo strany rotorov 1 a 2 a posledný je tiež pohľad z perspektívy, ale zo strany rotorov 3 a 4.
Ovládanie
Hneď na začiatku treba ozrejmiť, že ku modelu bude vytvorené iba ovládanie, nie riadenie. Riadenie quad-koptéry vyžaduje komplexné znalosti o metódach riadení takýchto procesov. Prvý spôsob ovládania bude realizovaný cez herný gamepad Genius G-12X so štvorsmerovým trackpadom a dvanástimi tlačidlami. Použitím bloku „joystick input“ je možné dostať do našej schémy signály generované gamepadom po stlačení jednotlivých tlačidiel. Pripojením bloku „display“ na výstupy bloku „joystick input“ sme najprv analyzovali poradie signálov z daného výstupu bloku. Po analýze bolo možné pristúpiť ku návrhu ovládania quad-koptéry. Prvým potrebným krokom bolo priradenie vlastností jednotlivým tlačidlám. To je znázornené na Obr. 5.
Obr. 5 Rozvrhnutie ovládacích prvkov Quad-koptéry na gamepade G-12X
Na stabilizáciu uhla vychýlenia quad-koptéry je potrebné vygenerovať periodický signál s jednou periódou. Samotné stlačenie tlačidla na gamepade však tento signál nevygeneruje, a preto bolo potrebné vymyslieť schému, na ktorej výstupe sa po stlačení tlačidla vygeneruje periodický signál s jednou periódou. Výslednú schému takéhoto generátora vidíme na Obr. 6.
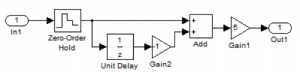
Obr. 6 Bloková schéma generátora periodického signálu obdĺžnikového tvaru s dobou jednej periódy
Blok „Zero-Order Hold“ sníma hodnotu z jeho vstupu s dobou vzorkovania tvz = 0.1s. Táto hodnota bola určená experimentálne. Pri takejto hodnote sa už nestávalo, že sa stlačenie a krátke držanie tlačidla vykonalo v medzičase odobratia vzoriek zo vstupu. Tento blok udrží hodnotu vstupu po dobu 0.1s. Zároveň hodnota putuje do bloku „Unit Delay“, kde je oneskorená o ďalších 0.1 a následne otočená v bloku „Gain2“, kde je vynásobená hodnotou -1. Pôvodná hodnota z bloku „Zero-Order Hold“ ako aj oneskorená a otočená hodnota putujú do bloku „Add“ kde sú sčítané do jedného signálu. Nakoniec je tento signál zosilnený päťnásobne, pretože by ináč jedno stlačenie tlačidla na gamepade naklonilo quad-koptéru len o veľmi malý uhol. Na Obr. 8 vidíme porovnanie ovládania quad-koptéry bez a s použitím generátora. Toto porovnanie bolo testované na schéme v Obr. 7. Táto schéma v jednoduchosti predstavuje schému quad-koptéry, pretože prenosová funkcia vyjadrujúca prenos uhlov quad-koptéry ku uhlovým rýchlostiam je druhého rádu.
Obr. 7 Bloková schéma pre test generátora periodického signálu s jednou periódou
Obr. 8 Časové priebehy výstupov sústavy druhého rádu s a bez použitia generátora
Posledným krokom k vytvoreniu kompletného bloku „Ovladanie“ bolo prepojenie všetkých potrebných blokov. Výslednú blokovú schému blok „Ovladanie“ vidíme na Obr. 9.
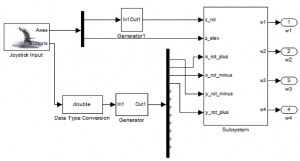
Obr. 9 Výsledná bloková schéma obvládanie s použitím gamepadu G12-X
Blok „Data Type Conversion“ je potrebný, pretože výstup „Buttons“ bloku „Joystick Input“ má typ „boolean“. Blok „Generator“ bol použitý iba vo vetvách, ktorými sa ovládajú uhly quad-koptéry. V bloku „Subsystem“ sa nachádzajú potrebné prepojenia vetiev na zabezpečenie správnych zmien uhlových rýchlostí.
Detekcia kolízie
Aby sme mohli zistiť či telo quad-koptéry nezasahuje do jednej z prekážok, alebo do steny, stropu či podlahy miestnosti, bolo potrebné vytvoriť tzv. blok detekcie kolízie. V tomto bloku zohráva hlavnú úlohu blok toolboxu Simulink 3D Animation VR Source, ktorý nám poskytuje informáciu o aktuálnych absolútnych (vztiahnutých ku svetovému súradnicovému systému) polohách jednotlivých kolíznych bodov. Najprv bolo potrebné do tohto bloku načítať ten istý VRML svet ako je načítaný v bloku VR Sink a zvoliť si vlastnosti ktorých objektov chceme sledovať. Samozrejme je potrebné pri výbere zvoliť absolútne hodnoty polohy (Obr. 10).
Obr. 10 Voľba sledovania absolútnych polôh kolíznych bodov
Tieto informácie ďalej putujú do blokov, v ktorých sa nachádzajú zadefinované priestory, ktoré sú vymedzené jednotlivými objektmi scény ako vidíme na Obr. 11. Do jednotlivých blokov „Interval Test“ sú zadané hodnoty, ktoré objekt v scéne zaberá pre jednotlivé osi. Ak je splnená podmienka na všetkých troch blokoch, splní sa zároveň aj podmienka na logickom hradle a simulácia sa zastaví.
Obr. 11 Blok detekcie pozície kolízneho bodu a objektu v priestore
Záver
Výsledkom práce je model quad-koptéry v prostredí Simulink s navrhnutým ovládaním a vytvorenou animáciou prostredníctvom jazyka VRML a toolboxu S3D. Tento komplexný model bude možné v budúcnosti využiť v predmetoch zaoberajúcich sa modelovaním a vizualizáciou procesov, alebo v bakalárskych a diplomových prácach pri návrhu rôznych typov riadení.
Literatúra
- Žára, J., „VRML 97 – Laskavý průvodce virtuálními světy“, ISBN: 80-7226-143-6
- Karban, P., „Výpočty a simulace v programech Matlab a Simulink“, ISBN: 80-2511-448-1, 2007
- Mathworks, „Simulink 3D Animation – Documentation“,
http://www.mathworks.com/help/pdf_doc/sl3d/sl3d.pdf - Teppo Luukonen, „Modelling and control of quadcopter“, School of Science, Espoo, August 22, 2011,
http://www.sal.tkk.fi/publications/pdf-files/eluu11.pdf
02. Február, 2013 o 19:37
Nezaškodilo by dajaké video zverejniť.