Simplified Model of WWER-440 Fuel Assembly for Thermo-Hydraulic Analysis

13. Február, 2013, Autor článku: Jakubec Jakub, Elektrotechnika
Ročník 6, číslo 2 This page as PDF Pridať príspevok

This work deals with thermo-hydraulic processes in fuel assembly using code ANSYS CFX 13. ANSYS CFX, which is commercial computational fluid dynamics (CFD) code applying the method of finite volumes to solve Navier-Stokes equations describing laminar and turbulent behavior of fluids with Reynolds-averaged Navier-Stokes equations (RANS) method. In order to understand the influence of shape of geometry and influence of boundary conditions on thermo-hydraulic processes several simplifications of geometry were made and gradually more boundary conditions were added.

1. Introduction

Detailed knowledge of the thermo-hydraulic processes is very important in the case of fuel assembly of nuclear reactors from the design and safe operation point of view. Investigations in this field can help improve possibilities of modern types of reactors. Experiments and CFD codes can help to accomplish these tasks. Main objective of this work is to develop validated CFD model for simplified one-sixth of the fuel assembly and in the future fully functional and validated CFD model for whole fuel assembly.

2. Navier-Stokes equations

CFD is a part of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. ANSYS CFX is CFD code that applies method of finite volumes to solve Navier-Stokes equations. Navier-Stokes equations are differential equations describing motion of fluid substances. They consist of differential equations of mass conservation, momentum conservation and energy conservation.

Equation (1) expresses mass conservation law, which is often called the equation of continuity because it requires no assumptions except that the density and velocity are continuum functions. That is, the flow may be either steady or unsteady, viscous or frictionless, compressible or incompressible [1]. It is partial differential equation involving the derivatives of density (ρ) and axis velocity (u,v,w).

\frac{\partial \rho}{\partial t} + \frac{\partial (\rho u)}{\partial x} + + \frac{\partial (\rho v)}{\partial y} + \frac{\partial (\rho w)}{\partial z} = 0 (1)

Momentum conversation law (2) is a fundamental law of nature, and it states that if no external force acts on a closed system of objects the momentum of the closed system remains constant. One of the consequences of this is that the center of mass of any system of objects will always continue with the same velocity unless acted on by a force from outside the system [2]. Variables in equations (2) are density (ρ), pressure in moving fluid (p), coefficient of viscosity (μ) and time (t).

\rho g_x - \frac{\partial p}{\partial x} + \mu \left ( \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} + \frac{\partial^2 u}{\partial z^2} \right ) = \rho \frac{du}{dt}

\rho g_y - \frac{\partial p}{\partial y} + \mu \left ( \frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2} + \frac{\partial^2 v}{\partial z^2} \right ) = \rho \frac{dv}{dt}

\rho g_z - \frac{\partial p}{\partial z} + \mu \left ( \frac{\partial^2 w}{\partial x^2} + \frac{\partial^2 w}{\partial y^2} + \frac{\partial^2 w}{\partial z^2} \right ) = \rho \frac{dw}{dt} (2)

Energy conservation law (3) is valid for a newtonian fluid under very general conditions of unsteady, compressible, viscous, heat-conducting flow, except that it neglects radiation heat transfer and internal sources of heat that might occur during a chemical or nuclear reaction [1]. Variables in equations (3) represents density (ρ), pressure in moving fluid (p), internal energy (û), velocity (V), nabla (∇), thermal conductivity (k), temperature gradient (∇T) and time (t).

\rho \frac{d \hat{u}}{dt} + p(\Delta . V) = \Delta (k \Delta T) + \phi (3)

3. Fuel assembly model

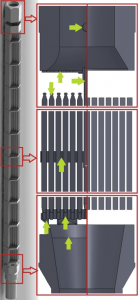
In the beginning accurate fuel assembly model was created (Fig.1).


Fig.1. Fuel assembly model

All calculations were made in ANSYS CFX, which is commercial computational fluid dynamics code applying the method of finite volumes. Since geometry of this model is complicated it would affect meshing process and it would make calculations much depended upon the hardware performance and the time. Because of this fact several simplifications were necessary to make.

4. Model simplifications and cavity

Simplifications for calculations were relatively large because it was necessary to find out suitable mesh properties and to test boundary conditions. With simpler geometry is plausible to change mesh properties and to run calculations in much shorter time. From the original model of fuel assembly grids (supporting grid, distant grids and mixing grid) and supporting grid handles were removed. Fuel rods were modeled like simple cylinders, rod handles and plugs were removed. Central tube was replaced by fuel rod (in thermal calculations heat flux on walls of central tube was 0 W/m2). And all fillets were removed. Model changes of fuel assembly can be seen in Fig.2.


Fig.2. Model simplifications

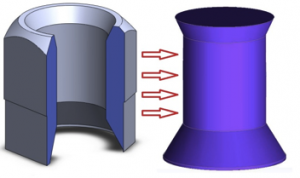
The main objective of this work is to analyze thermo-hydraulic processes of the flowing liquid so the cavity was created (Fig.3). The cavity is function of modeling program which creates mold from simplified fuel assembly model. Output is brand new model of internal volume of liquid. Due to the fact that geometry of fuel assembly is axial symmetric, one-sixth of model was sufficient for calculations (Fig.4).


Fig.3. Cavity sample


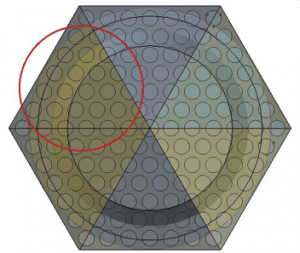
Fig.4. Symmetry of fuel assembly

5. Mesh

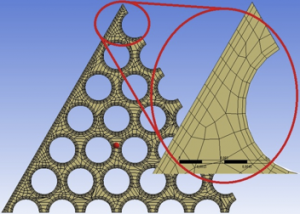
As the fluid moves past the object, the molecules right next to the surface stick to the surface. The molecules just above the surface are slowed down in their collisions with the molecules sticking to the surface. These molecules in turn slow down the flow just above them. The farther one moves away from the surface, the fewer the collisions affected by the object surface. This creates a thin layer of fluid near the surface in which the velocity changes from zero at the surface to the free stream value away from the surface. It is called the boundary layer because it occurs on the boundary of the fluid [2]. To capture this effect it was necessary to create mesh with inflated elements around the walls (Fig.5).


Fig.5. Inflation around walls

Parts were meshed with different methods. Foot, head and rods were sweeped with inflations and parts between were meshed with tetra-hedral elements and also with inflations (Fig.6)


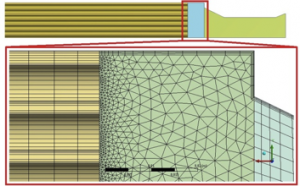
Fig.6. connections of different meshed parts

Used mesh has 297266 nodes and 380150 elements.

6. Boundary conditions

Next task was to specify the boundary conditions. It was necessary to find out inlet velocity, average heat flux, axial distribution of heat flux, inlet temperature and reference pressure of fluid to solve thermo-hydraulic behavior of fluid in simplified fuel assembly model in this case. Inlet velocity (vin) (equation 4. and 5.) was calculated from overflow by reactors coolant (QR), number of fuel assemblies in reactors core (NFA), coefficient which represents ratio of overflow by fuel assemblies to overflow by reactor (cFA) and inlet surface of fuel assembly.

Q_{FA} = \frac{Q_R}{N_{FA}}.c_{FA} (4)

v_{in} = \frac{Q_{FA}}{S_{in}}=4.1 m/s (5)

Average heat flux (q) (equation 6. and 7.) was calculated from thermal performance of reactor (WR), thermal performance of one fuel rod (Wrod), number of fuel rods in core (Nrod) and from fuel rod surface (Srod).

W_{rod} = \frac{W_{R}}{N_{rod}} (6)

q = \frac{W_{rod}}{S_{rod}}=434 kW/m^2 (7)

Axial distribution of heat flux can be seen in Fig.7.


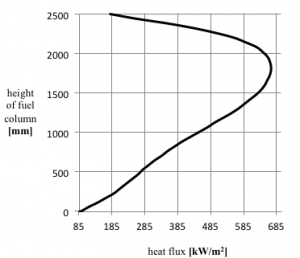
Fig.7. Axial heat flux distribution of selected fuel assembly

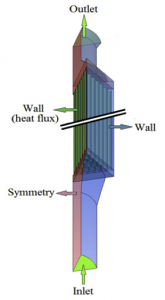
Inlet temperature: 268oC and reference pressure: 12,26 MPa. All used statements were from available resources. Turbulence model was used SST (shear stress transport) model. Boundary conditions assigned to surfaces can be seen in fig.8.


Fig.8. Boundary conditions

7. Simulations

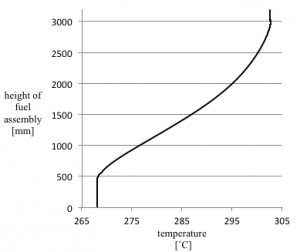
In order to study thermo-hydraulic behavior of fluid flowing through simplified fuel assembly several calculations were made. Simple adiabatic flow, flow with heat flux and flow with axial distribution of heat flux on fuel rod walls were calculated. Temperature increase in last calculation was 30˚C (Fig.14) and Reynolds number 223243 what corresponds with real conditions (Reynolds number in real fuel assembly is approximately 250000). Velocity profile (Fig.9) confirms correctness of calculations which shows increase in velocity gradient from wall to canal center – boundary layer.


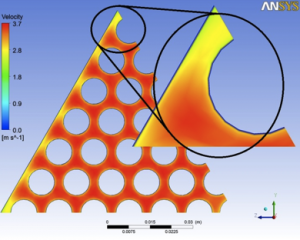
Fig.9. Radial velocity profile in fuel rods

Next two pictures show axial velocity distribution at the place where fluid leaves area of fuel rods (Fig.10 and Fig.11).


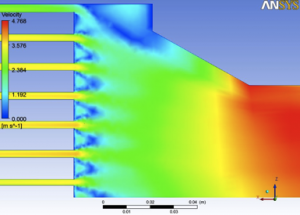
Fig.10. Axial velocity distribution (contour)


Fig.11. Axial velocity distribution (vector)

Next two pictures show velocity profile and temperature distribution on outlet surface (Fig.12 and Fig.13).


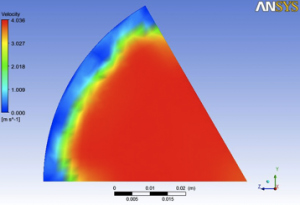
Fig.12. Outlet velocity distribution


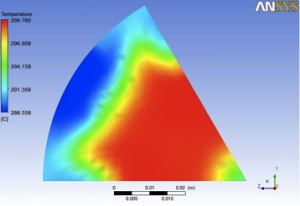
Fig. 13. Outlet temperature distribution

Last picture shows axial temperature increase from axial distributed heat flux on the walls.


Fig.14. Temperature increase

8. Conclusions

This paper describes options how to solve complicated geometries using several simplifications to gain correct results in simple analysis. Also it gives a background for next calculations. In further research of this work used ANSYS meshing program will not be possible to use. It will be necessary to use more precise meshing program to be able to make mesh with suitable properties. Next step will specify boundary conditions for different deployment of fuel assemblies in reactors core.

References

  1. Frank M. White: Fluid Mechanics: Fourth Edition
  2. NASA,
    http://www.grc.nasa.gov/WWW/k-12/airplane/boundlay.html
Co authors of the paper are doc. Ing. Vladimír Kutiš, PhD., Ing. Martin Petriska, Department of Applied Mechanics and Mechatronics, Faculty of Electrical Engineering and Information Technology, Slovak University of Technology in Bratislava

Napísať príspevok