Aplikácia Metódy Konečných Prvkov na rôzne, v dnešnej dobe rozšírené, typy elektrických prístrojov je hlavnou témou príspevku. Ten sa zameriava hlavne na elektro – tepelné analýzy počítačových modelov daných zariadení. Poukazuje na možnosti optimalizácie kritických miest, ako aj odstránenie hlavných nedostatkov formou odporúčaní.

Úvod

Prechod prúdu elektrickým prístrojom spôsobuje značné oteplenie prúdovej dráhy. Čím má prúd väčšiu amplitúdu, tým je oteplenie spôsobené prechodom výraznejšie. V niektorých prípadoch nestojí za námahu o tomto jave vôbec uvažovať, pretože oteplenie nie je ohrozujúce z pohľadu funkčnosti elektrického prístroja. Hlavnou myšlienkou tohto príspevku je zameranie sa na prístroje a prúdy, ktoré obmedzujú, alebo ohrozujú ich bezchybnú prevádzku. Teda dochádza k prudkému nárastu teploty vplyvom prechodu prúdu. Príspevok analyzuje dva typy elektrických prístrojov – stykač a zvodič prepätia. Pri prvom type ide o statické analýzy oteplenia prúdovej dráhy. V záverečnej časti je priblížený pohľad na optimalizáciu keramiky ZnO varistora, ako hlavného stavebného prvku zvodiča prepätia.

Elektrické teplo a jeho účinky na funkčnosť elektrických prístrojov

Vplyvom prechodu elektrického prúdu sa v elektrických prístrojoch generuje teplo. Čím je prúd väčší, tým je aj generovaný tepelný náboj väčší. Veľkosť generovaného tepla sa dá určiť pomocou rôznych metodických výpočtov. Hlavnú úlohu pri výpočte tvorí maximálna hodnota prúdu, čas jeho pôsobenia a objem cez ktorý prúd prechádza. Ďalšími dôležitými parametrami sú materiálové vlastnosti objemového telesa. Za základe určenia hodnoty generovaného tepla je možné následne pomocou prepočtu odvodiť hodnotu teplotného zaťaženia, teda hodnotu teploty, avšak v tejto fáze výpočtu zohráva úlohu aj umiestnenie objemového telesa a iné fyzikálne obmedzenia. Dôležitú úlohu zohráva prúdenie vzduchu v okolí skúmaného telesa. Odvod tepla z povrchu telesa je možné definovať pomocou koeficientu prestupu tepla do okolia – α.

(1)

kde Q predstavuje množstvo generovaného tepla, U je napätia a I prúd, τ predstavuje čas prechodu prúdu pri danom priloženom napätí.

(2)

kde m je hmotnosť telesa, c je jeho špecifické teplo a ΔT predstavuje teplotný rozdiel [1].

Stýkač

Stýkač je elektromagneticky ovládaný spínač pre časté spínanie elektrických obvodov s menovitými prúdmi v rozsahu desiatok až niekoľko stoviek A. Princíp činnosti spočíva v ovládaní kontaktného systému elektromagnetom. Stýkač a kontaktný systém je konštruovaný s ohľadom na špecifiká spínania výkonových (silových) elektrických obvodov (potreba zhášania vypínacieho oblúka po rozpojení obvodu a pod.)

Dimenzovanie prúdovej dráhy vychádza z menovitého prúdu a charakteru zaťaženia pričom oteplenie jednotlivých častí nesmie prekročiť normou dovolené hodnoty. Pritom treba zohľadniť aj tepelnú triedu izolantov, ktoré sú v dotyku s časťami prúdovej dráhy. Straty v elektrickom prístroji predstavujú určitú spotrebu elektrickej energie a bolo by žiaduce ich znížiť. Jednou z možností je zväčšenie prierezu a použitie materiálu s lepšou elektrickou vodivosťou. Táto cesta vedie však ku zvýšeniu ceny prístroja.

Niekedy sa zdá, že materiál prúdovej dráhy nie je dostatočne využitý, pretože z hľadiska mechanického je potrebný väčší prierez. Bolo by teda vhodné použiť materiál s vyššou mechanickou pevnosťou a menšou elektrickou vodivosťou (menej materiálu a nižšia cena – stúpnu však straty). Voľba správnej cesty je daná zásadami hospodárnosti aby cena prístroja a cena strát boli minimálne. Z hľadiska dimenzovania prierezov prúdovej dráhy sa uvažuje s trvalým zaťažením a kontrolou oteplenia [2].

Varistor

Varistor je nelineárny a tepelne závislý rezistor s nelineárnou V-A charakteristikou, ktorá mu umožňuje širokú škálu uplatnenia. Varistory boli v minulosti vyrábané z karbidu kremíka SiC, ktorý časom nahradila chemická zlúčenina oxid zinočnatý ZnO pre lepšie a komplexnejšie vlastnosti počas pôsobenia voči prepätiu. Chemické zloženie je tvorené z 95% zmesou oxidov kovov. Zvyšných 5% tvoria prímesi Bi₂O₃, TiO₂, CoO, MnO a Sb₂O₃, ktoré sa podieľajú na nelinearite a stabilite varistora. Varistory sú vyrábané sintrovaním zo spekaného granulátu oxidu zinočnatého spolu so spomínanými prímesami pri teplote od 1250 – 1400 °C, v závislosti od triedy použitia. Na hraničných miestach zŕn sa vytvárajú polovodivé rozhrania, ktorých princíp je rovnaký ako pre polovodivé p-n priechody [3].

Modelovanie elektrických prístrojov

Modely sú v základnom ponímaní rozdelené na dve hlavné skupiny, fyzikálne a pravdepodobnostné. Rozdiel medzi fyzikálnym a pravdepodobnostným modelom je v tom, že fyzikálny model sa zameriava hlavne na simuláciu šírenia impulzu, ktorého riešením je súbor rovníc pre zachovanie momentovej a energetickej rovnice ako aj rovnice kontinuity. Niektoré modely sa využívajú na deriváciu parametrov pre praktické použitie ako U50 prerušeného napätia, rýchlosť impulzu, čas prerušenia a výpočet impulzného prúdu. Na druhú stranu ich komplexnosť má aj niektoré nevýhody, ako napríklad absencia schopnosti obnoviť náhodné správanie trajektórie šírenia a vetvenia impulzu.

Pravdepodobnostné modely sú založené primárne na elektrickom poli a využívajú pravidlá pravdepodobnosti k predpovedaniu ako sa budú šíriť kanály. Možnosť reprodukovať náhodné správanie trajektórie šírenia a schopnosť 3-D simulácie dávajú týmto modelom širokú škálu využitia [4]. Hlavným rozdielom medzi MKP a inými numerickými metódami je voľba funkcií pre podoblasti konečných rozmerov, na ktoré je oblasť diskretizovaná. Konečné prvky majú tvar čiary, plochy alebo objemu konečných rozmerov. Vyššia presnosť riešenia úlohy je priamo závislá na jemnosti siete konečných prvkov.

Riešenie úlohy metódou konečných prvkov je možné všeobecne rozdeliť do nasledujúcich bodov: 1. definícia fyzikálneho modelu a okrajových podmienok jednoznačnosti riešenia, 2. diskretizácia analyzovanej oblasti na sieť konečných prvkov, 3. identifikácia primárnych neznámych a voľba interpolačných funkcií poľa, 4. definícia konštitutívneho vzťahu medzi akciami a reakciami riešeného poľa, 5. odvodenie prvkových rovníc, 6. odvodenie rovníc MKP celej riešenej oblasti s riešením primárnych neznámych, 7. výpočet sekundárnych neznámych, 8. interpretácia dosiahnutých výsledkov a optimalizácia riešenej úlohy [5].

Model prúdovej dráhy stykača

Pri modelovaní sme použili stýkač s menovitým prúdom 100 A. Riešili sme prúdovú dráhu stredného pólu. Hlavný zámerom je modelovanie teplotného poľa pri zaťažení trvalým prúdom 100 A.

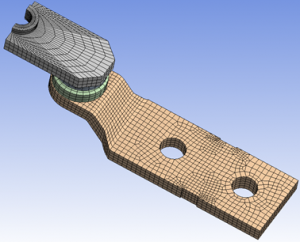
Obr. 1 Sieť konečných prvkov modelu stykača

Model je charakterizovaný niektorými špecifickými modifikáciami, ktoré majú za úlohu reprodukovať čo najreálnejšie okrajové podmienky, avšak niektoré vlastnosti modelu sú do istej miery zjednodušené. Výhodou modelu je uvažovanie nie ideálneho spojenia kontaktov, ale predpokladanie iba obmedzeného počtu miest styku medzi kontaktmi. Model predpokladal aj vplyv koeficientu prestupu tepla konvekciou.

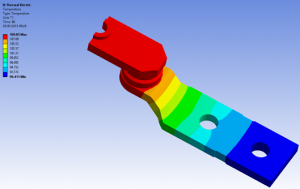
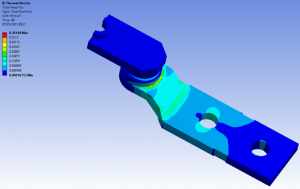
Obr. 2 Teplotné pole po prechode prúdu

Obr. 3 Pole tepelného toku

Na Obr. 2 a 3 je možné pozorovať výsledky elektrotepelnej analýza modelu stykača. Pomocou koeficientu prestupu tepla bolo možné korektne definovať geometrické umiestenie systému stykových kontaktov bloku stykača, teda z pohľadu ochladzovania okolím v podstatne obmedzených podmienkach. Podľa očakávanie je najteplejším miestom práve miesto styku a to aj z dôvodu definovania počtu stykových plôch. Obr. 3 prezentuje teoretické usporiadanie poľa tepelného toku.

Práve riešenie stykového miesta prináša značné problémy pri návrhu geometrického modelu styku. Reálne sa kontakty dotýkajú v obmedzenom počte bodov a preto sme zvolili pri riešení „bodový styk“ kontaktov. Teplotné pole polovice miesta styku vzhľadom na symetriu je na obr. 4a pre typickú hodnotu stykového odporu. Vzhľadom na zmeny stykového odporu počas prevádzky je na obr. 4b pole pre 5- násobok typickej hodnoty stykového odporu, pričom maximálna teplota vzrástla o takmer 30 ^oC [6].

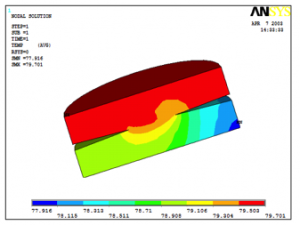
(a)

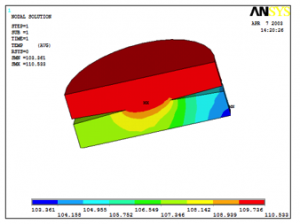
(b)
Obr. 4 Teplotné pole stykového miesta.

2D Model varistora

Za účelom modelovania a optimalizácie bol navrhnutý počiatočný 2D model varistora typu V350P43SP, pričom hlavnú časť tvorí ZnO keramika. Model varistora je založený na rovnakom fyzikálnom princípe ako model stykača.

Obr. 5 Sieť konečných prvkov 2D modelu varistora

Jedným z účelov simulácií modelu varistora na báze oxidov kovov je štúdia degradácie a deštrukcie tohto stavebného prvku. Spomínané sprievodné javy sú následkom prúdového preťaženia ZnO keramiky. Prechod prúdu s vyššou amplitúdou než je nominálna hodnota udávaná výrobcom spôsobuje nárast teploty nad limity materiálových vlastností. Nevýhodou modelu je smer šírenie tepla iba do bočných strán vzhľadom na 2D geometriu. Proces odovzdania tepla je aj napriek tomu pomerne rýchly.

Obr. 6 Rozloženie teplotného poľa v čase úplného zániku energie bleskového prúdu

Veľkou nevýhodou predkladaného modelu varistora je pomerne náročný proces overenia dôveryhodnosti dosiahnutých výsledkov, ktorý sa konkrétne týka teploty v mieste prechodu impulzu prúdu. Na základe jednoduchších meraní je možné porovnať teplotu na povrchu epoxidovej izolácie. Na základe dosiahnutých výsledkov modelu a experimentu sú odchýlky minimálne.

Obr. 7 Priebeh teplôt na povrchu epoxidu pre tri hodnoty prúdu

Hlavnou devízou predkladaného modelu varistora je jeho vzájomne previazaná elektrická a tepelná analýza. Aktuálny návrh zohľadňuje širokú škálu možností pre aplikáciu rôznych hodnôt bleskových prúdov. Z tohto dôvodu sa vyskytujú malé odchýlky pri porovnaní priebehov pre 6, 9 a 12,5 kA.

Záver

Metóda konečných prvkov je jedna z popredných výpočtových metód, ktorej škála uplatnenia je veľmi široká. Z pohľadu riešenia úloh teplotného poľa ja vhodné využiť túto metódu pre potreby zistenia kritických bodov oteplenia elektrických prístrojov. Stykač a varistor sú bežne využívané elektrické prístroje, ktorými pri aktívnom pôsobení tečú špecifické hodnoty elektrického prúdu. Každý z nich má odlišný systém funkčnosti, ku ktorému sa priamo viaže aj tvorba teplotného poľa. Teplotné poľa má podstatný vplyv hlavne pri varistore kedy je nápomocné pre vznik prierazu a znehodnoteniu tohto elementu. Príspevok sa zameral na využitie MKP pri simuláciách a tvorbe teplotných polí. Hlavným prínosom je sledovanie kritických miest oteplenia prúdovej dráhy a kritických miest.

Literatúra

1. Kalousek M., Hučko B. (1996): Prenos Tepla, 1. vydanie. Bratislava STU 1996. ISBN 80-227-0881-X. 212 s.
2. Základné informácie o stykači (2012): internetový zdroj:
   http://sk.wikipedia.org/wiki/St%C3%BDka%C4%8D
3. Dudáš J. (2006): Principy konstrukce a funkce varistorových svodičů přepětí. Elektro – odborný časopis pro elektrotechniku, ročník 2006, číslo 05.
4. Charalambakos V. P., Pyrgioti E. C. (2006): Computer Simulation of Lightning Strokes. 28th International Conference on Lightning Protection, Kanazawa, Japan, 163-168.
5. Murín J. (2012): Metóda konečných prvkov – Aplikovaná mechanika – prednáška. Zdroj:
   kmech.elf.stuba.sk/dokumenty/APLIMECH/prednaska_c2.pdf
6. Hüttner, Ľ., Valent, F., Kutiš, V., Murín, J. (2013): Solution of temperature fields in electric devices. In: Proc. of XVth Symposium on Physics of Switching Arc, Volume I. Contributed papers, Brno, Czech republic, september 22-26, 2003, pp.75-78.
7. Király R. (2012): Diplomová práca. Bratislava: FEI STU 2012.
8. Glasa M. (2013): Elektro – tepelná analýza varistora na báze oxidov kovov. Dizertačná práca. Bratislava: FEI STU 2013. 73s.

---

Spoluautormi článku sú Róbert Király, Ľudovít Hűttner,