Článok pojednáva o jednom segmente z Business intelligence – Data mining. V článku sa nachádza charakteristika, história data mining-u. Taktiež sa článok zaoberá modelmi a metódami, algoritmami ako aj samotnou aplikáciou dolovania dát. V závere je vysvetlený celý proces data mining-u. Od zberu a integrácie dát cez analýzu až po predikciu a interpretáciu dosiahnutých výsledkov.

1. Úvod

Dolovanie dát, resp. známejší anglický pojem Data mining je náročný proces, ktorý sa využíva v rôznych oblastiach. Je možné sa s ním stretnúť tak vo finančníctve, bankovníctve ale aj v telekomunikáciách, biofarmaceutickom priemysle, bezpečnostných technológiách a v iných odvetviach, v ktorých je potrebné efektívne spracovať a „dolovať“ dáta na neskoršie použitie pri procese rozhodovania. Vzhľadom k tomu, že technologický vývoj napreduje veľmi rýchlo a objem dát sa tým pádom tak isto zväčšuje, bolo potrebné vytvoriť komplex metód a modelov, ako z veľkého množstva dát, za rozumný čas dostať relevantné výsledky na základe vstupných podmienok. Celkový proces však nie je taký jednoduchý. Práve preto má tento článok za úlohu vysvetliť proces data mining – u ako celku, od vymedzenia pojmov, cez základné teoretické znalosti, ako aj aplikácie a využitie data mining – u v praxi.

2. História data mining – u

Samotný pojem Data mining (DM) je pomerne mladý. Predstavený bol až v roku 1990, ale evolúcia data mining – u ako vednej disciplíny siaha do hlbšej minulosti. Začiatky DM siahajú do čias, kedy sa vyvíjala klasická štatistika, umelá inteligencia a tzv. machine learning [1]. Tieto obory mali vplyv na DM a zároveň v začiatkoch deväťdesiatych rokov dvadsiateho storočia si DM získaval popularitu hlavne v marketingovej a bankovej sfére. Neskôr sa techniky zdokonaľovali a viedlo to k uplatneniu aj v iných oboroch [2]. Okrem vyššie uvedených využití je data mining neoddeliteľnou súčasťou Business Intelligence (BI) a patrí medzi najrýchlejšie rastúci a vyvíjajúci sa segment v rámci BI [3].

3. Pojem data mining

Čo sa týka pojmu data mining, definícia znie: „Data mining je proces analýzy dát z rôznych perspektív a ich premena na užitočné informácie. Z matematického a štatistického hľadiska ide o hľadanie korelácií, teda vzájomných vzťahov alebo vzorov v dátach“ [3]. Inak povedané, ide o hľadanie, dolovanie a odkrývanie dát a informácií pre podporu rozhodovania z existujúcich dátových zdrojov [3]. V praxi sa často vyskytuje veľké množstvo dát, pri ktorých je potrebné sa zamerať len na určité informácie. Práve tieto informácie sa snaží DM tzv. „vydolovať“. Takto získané informácie sa následne používajú pri rozhodovaní a ich využitím by sa mal dosiahnuť merateľný ekonomický efekt. Taktiež DM môže pomôcť pri identifikácii problému a identifikácii existujúcich alebo pravdepodobných vzájomných vzťahov medzi jednotlivými entitami [3].

4. Úlohy dolovania dát

• Exploračné analýzy – v tejto analýze je cieľom preskúmanie dát bez predchádzajúcich znalostí.
• Deskriptívne úlohy – popísanie dátovej množiny. V týchto úlohách sa využíva metóda zhlukovania podobných javov, dát.
• Prediktívne úlohy – majú za cieľ na základe dátovej množiny a jej chovania, určiť resp. predpokladať budúce chovanie alebo jej hodnotu.
• Hľadanie vzorov a pravidiel – hľadajú sa vzory a vzťahy medzi dátami v množine.
• Hľadanie podľa vzorov – vyberanie z dát takých údajov, ktoré sa podobajú na vzor, podľa ktorého sa vyhľadáva [10].

5. Metódy a modely

5.1. Štatistika a data mining

Ako bolo spomínané vyššie, DM využíva pri získavaní relevantných dát štatistický a matematický aparát. Preto je potrebné vysvetlenie základných pojmov ako hypotézy, korelácia a iné. Data mining je zo štatistického hľadiska založený na už spomínaných hľadaniach korelácií a testovaní hypotéz. Na to, aby sme mohli testovať hypotézy, potrebujeme poznať rozdelenie pravdepodobností. To sa rozdeľuje podľa typu náhodnej veličiny na spojité a diskrétne. V prvom prípade sa najčastejšie využíva Gaussovo normálové rozdelenie, ktoré spočíva v jednoduchej funkcii, symetrickej okolo strednej hodnoty m. Náhodná veličina X má v súbore normálne rozdelenie závislé na dvoch parametroch:

• Strednej hodnote m
• Smerodajnej odchýlke s

Šírku krivky (v inflexnom bode) udáva práve smerodajná odchýlka s [4].

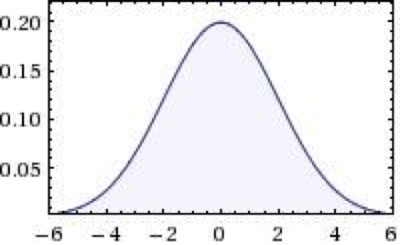
Obrázok 1 Gaussovo normálové rozdelenie

Na obrázku č. 1, je možné vidieť Gaussovo normálové rozdelenie, ktoré nám hovorí, že najväčší výskyt hodnôt je práve v bode 0. Ak si to vztiahneme na praktický príklad klasifikácie stupnicou A až E a budeme 0 (stred rozdelenia) považovať za klasifikačnú známku C, tak práve najviac známok je C. Pravdepodobnosť výskytu ostatných známok klesá spoločne s krivkou. Tzn. že výskyt známok B (D), je menej pravdepodobný ako C a výskyt známky A (E) je menej pravdepodobný ako známky C (ale aj B (D)). Oproti spojitej náhodnej veličine, diskrétne rozdelenie nie je funkcia definovaná na spojitom intervale, ale sú to izolované body na reálnej osi. Na zobrazenie sa používa stĺpcový graf, kde každý stĺpec má svoju hodnotu. Medzi takéto diskrétne chovanie môžeme považovať práve hod kockou.

5.2. Hypotézy

V štatistike, hypotéza je rozhodnutie, či nejaké tvrdenie o parametroch náhodnej veličiny alebo o veličine samotnej, ktoré je pravdivé alebo nie [5]. Stanovenie tejto hypotézy prebieha ešte pred samotným meraním danej veličiny. Avšak, musíme mať dopredu nejaké poznatky, na základe ktorých môžeme danú hypotézu navrhnúť. To, či daná hypotéza je platná alebo nie, nie je možné matematickým postupom stanoviť. Na základe štatistických pozorovaní rozhodneme o:

• Zamietnutie hypotézy
• Nezamietnutie hypotézy

V prípade, že hypotézu nezamietame, dochádza k faktu, že nevieme, či hypotéza platí alebo máme málo informácií [5]. Fakt, že danú hypotézu nezamietneme, neznamená, že ju aj potvrdíme, teda že je správna. V takomto prípade, ak v takejto hypotéze bude aspoň jeden výskyt pravdivej hodnoty zaznamenaný, môžeme tvrdiť o hypotéze, že je aj pravdivá. Overovaná hypotéza musí patriť do tzv. prípustných hypotéz, ktoré sú aspoň čiastočne špecifikované. Takáto hypotéza sa nazýva aj nulová, oproti ktorej nami zvolenú hypotézu budeme testovať [3]. Pri zamietnutí alebo nezamietnutí, sa dopúšťame dvoch chýb.

• Chyba prvého druhu – ak hypotéza platí, ale hypotéza bola zamietnutá
• Chyba druhého druhu – ak hypotéza neplatí, ale hypotéza nebola zamietnutá

V tabuľke č. 1 je možné vidieť obe chyby proti skutočnosti a rozhodnutiu [5].

Tabuľka 1 Chyby pri testovaní hypotéz

H	Platí	Neplatí
Zamietneme Chyba 1. druhu (α)	Chyba 1. druhu (α)	-
Nezamietneme	-	Chyba 2. druhu (α)

5.3. Štatistické metódy v data mining – u

Ako bolo vyššie spomenuté, okrem hypotéz DM využíva koreláciu, lineárnu a logistickú regresiu či predpovedajúce metódy. Pri zložitejších metódach, prichádzajú na rad neurónové siete prípadne genetické algoritmy [3].

Korelácia je miera závislosti medzi dvoma premennými [3]. Význam korelácie v DM je pri hľadaní takých hodnôt, ktoré majú na seba vplyv vo fáze rozhodovania. V praxi ide napr. o výber bankových produktov pre vekovú skupinu mladých ľudí do 25 rokov. To znamená, že ak mladý ľudia majú záujem o bezplatný účet, banka môže taktiež ponúkať takýmto zákazníkom študentskú kartu ISIC. Prípadne ak v nejakom časovom období je veľký dopyt po nejakom tovare, je pravdepodobné, že okrem tohto tovaru budú zákazníci potrebovať aj iný tovar. Práve korelácia je spôsob, ako je možné v DM nájsť druhý tovar, ktorý by bolo možné predávať spoločne.

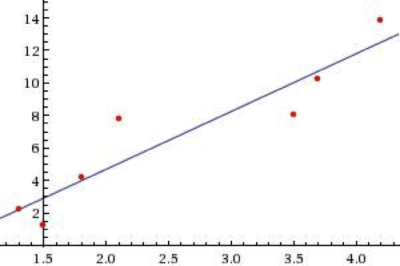
Lineárna regresia je štatistická metóda, ktorá kvantifikuje závislosť medzi dvoma spojitými premennými: závislou (snažíme sa predikovať) a nezávislou – prediktívna premenná. Princípom je nájdenie priamky, ktorá prechádza jednotlivými bodmi. Platí, že súčet druhých mocnín odchýlok od každého bodu je minimálny. Cieľom je dosiahnutie lineárneho preloženia. V prípade nedosiahnutia takéhoto preloženia, je nutné zmeniť nezávislú premennú, aby sme dostali lepšie preloženie [3]. Na obrázku č. 2 je vidieť jednoduchý príklad na lineárnu regresiu.

Obrázok 2 Lineárna regresia

6. Algoritmy data mining – u

Keďže Data mining sa snaží hľadať korelácie a vzťahy medzi jednotlivými dátami, nasledovné techniky okrem týchto štatistických a matematický metód využívajú i umelú inteligenciu prípadne clustering (zhlukovanie).

6.1. Asociačné pravidlá

Cieľom je nájsť spojenia medzi atribútmi obsiahnutými v databáze. Táto technika je známa ako Nákupný košík. Je založená na frekvencii a počte nakúpených položiek a percentuálne zastúpenie jednej položky pri kúpe druhej položky [1]. V praxi to znamená rozmiestnenie produktov tak, aby boli spoločne nakupované produkty blízko seba.

6.2. Nevyvážené rozpadové stromy

Tento algoritmus sa snaží odhaľovať závislosti a vyhľadáva špecifické vlastnosti, ktoré sú využité na vytvorenie predikčného modelu rozhodovania na jednotlivých úrovniach hierarchickej štruktúry [1].

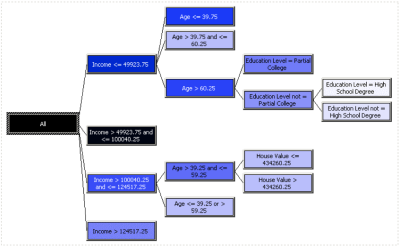
Obrázok 3 Rozhodovací strom [7]

6.3. Zhlukovanie (Clustering)

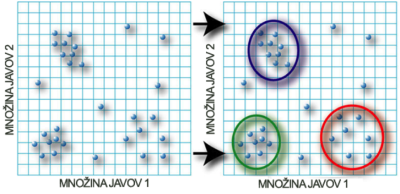
Slúži na vyhľadávanie podobných množín dát a ukladá ich do skupín. Zhlukovanie patrí medzi nepriame získavanie vedomostí [1].

Obrázok 4 Zhlukovanie [8]

Na obrázku č. 4 je v ľavej časti plná množina dát pred procesom zhlukovania. Na základe vlastností pre určitý druh dát, sa tieto dáta zoskupujú do sekcií, ako je vidieť v pravej časti obrázku č. 4.

6.4. Naive Bayes

Tento algoritmus je založený na Bayesovej vete. Tá pracuje práve s pravdepodobnosťami, kde výskyt náhodnej veličiny A za podmienky, že sa vyskytne udalosť B sa rovná podielu prieniku pravdepodobností udalostí A a B a pravdepodobnosti B. Tento algoritmus je veľmi rýchly a pomerne presný a využíva sa pri zložitejších analýzach [3].

6.5. Neurónové siete

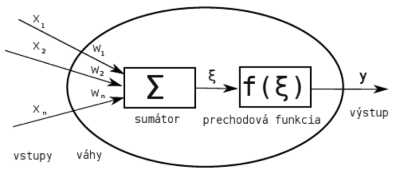
Táto metóda nevychádza zo žiadneho štatistického rozdelenia, ale pracuje podobne ako ľudský mozog, pričom sa snaží rozpoznávať vzory a minimalizovať chyby. Prakticky ide o prijímanie informácií a na základe podmienok sa sieť učí a získava skúsenosti. Samotná neurónová sieť je zložená z uzlov, ktoré sú pospájané do vrstiev. Najskôr sa musí vytvoriť tréningová a testovacia množina. Počas iterácií sú spracované vstupy porovnané so skutočnou hodnotou. Zmerajú sa chyby a spracujú sa systémom aby ten upravil váhy. Proces končí vtedy, keď sa dosiahne dopredu určenej minimálnej odchýlky.

Obrázok 5 Schéma neurónu [9]

7. Aplikácie data mining – u

Data mining je možné použiť v rôznych aplikačných doménach. Pomerne rozšírená je aplikácia v bankovníctve a poisťovníctve, ďalej v biofarmaceutickom priemysle na zisťovanie efektívnosti nových liekov, v telekomunikačnom priemysle. Data mining má taktiež využitie pri odhaľovaní finančných alebo poisťovacích podvodov, odhadovanie rizík, dolovanie dát z textu, prípadne diagnózy v medicíne a iné. Samozrejme nemôžeme zabudnúť spomenúť Business Intelligence, kde DM je súčasťou tohto komplexného procesu využívania a extrahovania informácií z množstva dát.

8. Data mining proces

Proces DM je založený na iteratívnom prístupe a induktívnych učiacich metódach, ktorých hlavným cieľom je odvodenie základných pravidiel začínajúcich na množine dostupných vzoriek dát, pričom obsahuje záznamy z minulých pozorovaní uložených v jednej alebo viacerých databázach. Aktivity DM môžeme rozdeliť do dvoch hlavných vetiev, v závislosti na účele analýzy:

• Interpretácia
• Predikcia

Účelom interpretácie je identifikácia regulárnych vzorov v dátach a ich vysvetlenie pomocou pravidiel a kritérií tak, aby boli ľahko pochopiteľné pre expertov. Generované pravidlá musia byť originálne a netriviálne, aby prakticky zvýšili úroveň znalosti a pochopenia daného problému. Na druhej strane predikcia má za úlohu predvídať hodnotu, ktorú bude náhodná premenná obsahovať, alebo odhadnúť pravdepodobnosť budúcich udalostí [6]. Na obrázku č. 6 je zobrazený proces DM.

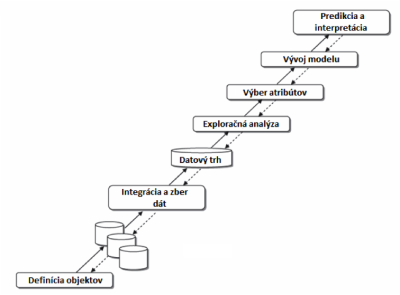
Obrázok 6 Data mining process [6]

V prvom kroku je potrebné definovať samotný problém. Riešením tohto problému bude výsledok DM procesu, teda výstup, na základe ktorého je možné robiť rozhodnutia. V prípade, že daný problém nie je dobre definovaný, môže dôjsť k odchýlkam či chybám.

8.1. Zber dát a integrácia

Ak je cieľ a problém jasne definovaný, pristupuje sa k získavaniu a integrácii dát. Tie môžu byť z rôznych zdrojov a môžu byť interné, externé alebo kombinované. Interné vznikajú v rámci firmy, sú uložené v databázach, prípadne dátových skladoch. Medzi externé zdroje môžeme považovať dáta, ktoré firmy môžu využiť od externých dodávateľov [2].

8.2. Skúšobná analýza

V tomto kroku sa pristupuje k predbežnej analýze dát z ktorých sa dostávajú znalosti a následne sa pristupuje k čisteniu dát. Zvyčajne, takéto čistenie prebieha v dátových skladoch a odstraňujú sa väčšinou syntaktické nekonzistentnosti [6].

8.3. Výber atribútov

Táto fáza sa zaoberá vhodnosťou atribútov na základe vzťahov k cieľu celého procesu. Tie atribúty, ktoré majú malú významnosť sú vylúčene, čím sa dosiahne ďalšieho čistenia nepotrebných informácií zo skúmanej dátovej množiny. Taktiež, nové atribúty z pôvodných premenných sú pridané do dátovej množiny [6].

8.4. Rozvoj a overenie

Model môžeme vyvinúť až po tom, ak je množina dát považovaná za kvalitnú. Tá vznikne pridaním definovaných atribútov. Okrem atribútov je potrebné do množiny vložiť prediktívne modely prípadne modely na rozpoznávanie vzor. Najskôr sa vytvorí tréningový model, ktorý využíva vzorky z pôvodnej množiny dát. Následná presnosť predikcie každého modelu je ohodnotená, a tá ktorá ma najlepšie výsledky pokračuje v práci s ostatnými dátami. Veľkosť tréningovej množiny dát je pomerne malá, odporúča sa pár tisíc záznamov[6].

8.5. Predikcia a interpretácia

Posledný krok v data mining procese. Slúži hlavne pri rozhodovacích procesoch a získavaní ďalších znalostí. Ako už bolo povedané vyššie, tento proces je založený na iteratívnych prírastkoch. Na obrázku 6, je vidieť bodkované čiary, ktoré naznačujú možnosť vrátenia sa do predchádzajúcej fázy [6]. Tým pádom sa môžeme vrátiť o iteráciu späť a v prípade zlých výsledkov zmeniť parametre.

9. Záver

Data mining je pomerne rýchlo sa vyvíjajúce odvetvie a má veľmi široké uplatnenie. DM nachádza uplatnenie od finančníctva cez telekomunikácie až po Business Intelligence. V týchto odvetviach sa nachádza veľké množstvo dát, z ktorých je potreba vybrať vhodné dáta pre napr. následné rozhodovanie. Práve Data mining túto úlohu spĺňa veľmi dobre, pretože pracuje s koreláciami, regresiou a v zložitejších prípadoch využíva neurónové siete. Tieto štatistické metódy a metódy umelej inteligencie pomáhajú DM pri dolovaní dát, ďalej pri tzv. knowledge discovery alebo pri procese rozhodovania, kde má nezastúpiteľné miesto.

Literatúra

1. KEE HO, Wing a Xiaohua LUAN. Data minning. University of North Carolina at Chapel Hill | The University of North Carolina at Chapel Hill [online]. 1. vyd. North Carolina, 2003 [cit. 2013-04-03]. Dostupné z:
   http://www.unc.edu/~xluan/258/datamining.html#history
2. PETR, Pavel. Data Mining. Vyd. 2. Pardubice: Univerzita Pardubice, 2008. ISBN 978-807-3950-989.
3. LACKO, Luboslav. Business Intelligence v SQL Serveru 2005: reportovací, analytické a další datové služby. Vyd. 1. Brno: Computer Press, 2006, 391 s. ISBN 80-251-1110-5.
4. BEDÁŇOVÁ, Iveta a Vladimír VEČEREK. Základy statistiky pro stud ující veterinární medicíny a farmacie [online]. Brno, 2007 [cit. 2013-04-03]. Skriptá. Veteriní a farmaceutická univerzita Brno. Vedoucí práce Vladimír Večerek. Dostupné z:
   http://cit.vfu.cz/stat/fvl/Skripta.pdf
5. BEDNÁŘ, Josef. Testování statistických hypotéz [online]. Brno, 2006, s. 8 [cit. 2013-04-03].
6. VERCELLIS, Carlo. Business intelligence: data mining and optimization for decision making [online]. Chichester, U.K.: Wiley, 2009, s. 18 [cit. 2013-04-03]. ISBN 978-0-470-51138-1.
7. Performance Study of Microsoft Data Mining Algorithms. TANG, Zhaohui a Jim YANG. MICROSOFT. Resources and Tools for IT Professionals | TechNet [online]. 2000, 25.3.2002 [cit. 2013-04-03]. Dostupné z:
   http://technet.microsoft.com/en-us/library/cc917687.aspx
8. VISUAL DATA MINING: The Possible Future of Using Star Cluster Formation Computer Models to Analyze Social Networks. San Francisco State University [online]. San Francisco, 2007 [cit. 2013-04-03]. Dostupné z:
   http://userwww.sfsu.edu/art511_h/acmaster/Project1/project1.html
9. Optimalizácia Hopfieldovou sieťou – 1. časť. Web o it [online]. 2008, 25.9.2009 [cit. 2013-04-03]. Dostupné z: http://www.weboit.sk/clanok/131/optimalizacia-hopfieldovou-sietou-1-cast.htm
10. NOVOTNÝ, Ota. Business intelligence: jak využít bohatství ve vašich datech. 1. vyd. Praha: Grada, 2005, 254 s. ISBN 80-247-1094-3.

---

Fakulta aplikované informatiky, Univerzita Tomáše Bati ve Zlíně