V súčasnosti sa pri rôznych programových aplikáciách stretávame s výpočtovo náročnými či už matematickými alebo všeobecnými operáciami, ktoré spracovávajú veľké množstvo dát. Zrýchlenie takýchto časovo náročných výpočtov sa zvyčajne realizuje samotným zvýšením výpočtového výkonu počítača alebo distribúciou výpočtov na jednotlivé jadrá procesora pri viacjadrových počítačoch. Takéto riešenie však vyžaduje značnú investíciu do hardvérového vybavenia. Iným prístupom ako urýchliť výpočet matematických operácií je použiť na výpočet grafickú kartu.

Urýchlenie výpočtov na grafickej karte

Urýchľovanie všeobecných výpočtov na grafických kartách sa masívne rozšírilo v roku 2007, keď spoločnosť nVidia vydala prvú oficiálnu verziu aplikačného rozhrania na všeobecné výpočty na grafických kartách. Toto rozhranie sa volá CUDA – Compute Unified Device Architecture a umožňuje programátorom využívať masívny paralelný výkon moderných grafických kariet, ktoré boli doteraz určené na zábavu a počítačové hry [3].

Grafické karty donedávna počítali grafické výkony za pomoci takzvaných vertexových a pixelových jednotiek. Pri moderných hrách sa stávalo že sa občas využívali iba pixelové jednotky a tie vertexové nemali v tú chvíľu čo robiť a boli nevyťažené. Preto firma nVidia v novej sérii grafických kariet rady 8000 predstavila novú architektúru, ktorá nepoužíva oddelené vertexové a pixelové jednotky, ale na všetky typy výpočtov používa takzvané unifikované stream procesory. Tieto stream procesory sú všetky rovnaké a dynamicky si delia výpočtové úlohy podľa potreby a záťaže. S vydaním CUDA rozhrania majú programátori možnosť pracovať s týmito procesormi a spracovávať na nich iné ako grafické dáta. V dnešnej dobe sa grafické karty s CUDA využívajú vo vedeckých a výskumných centrách rôznych univerzít v odvetviach, ako biológia, medicína, fyzika, astrofyzika, umelá inteligencia, chémia, atď. [3, 7].

Kebyže porovnáme jeden stream procesor a jeden procesor základnej jednotky (CPU – central processing unit), tak určite s prehľadom vyhrá CPU. Sila grafickej karty je v paralelnom spracovaní dát. Na jednom grafickom čipe sa bežne nachádzajú stovky týchto stream procesorov a v ich kombinovanom výkone ďaleko prevyšujú výkon CPU. Výpočtovú grafickú jednotku tvorenú stream procesormi a pamäťou grafickej karty v skratke označujem ako GPU – graphics processing unit (viď. obr.1).

Na porovnanie teoretického výpočtového výkonu CPU a GPU sa používa počet vykonateľných operácií s desatinnou čiarkou za sekundu (*flop – float point operations per second). Napr. dvojjadrový procesor CPU Core 2 Duo E7400 má výpočtový výkon 22,4 Gflop* a na porovnanie grafická karta Geforce GTS 250 so 128 stream procesormi má výpočtový výkon 700Gflop*. Z týchto údajov je vidno že takáto grafická karta má približne 28 násobný výkon oproti CPU [6].

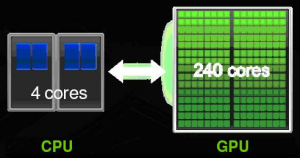
Obr.1: Porovnanie CPU a GPU (jadrá – cores)

Samozrejme že nie každý problém sa dá dobre paralelizovať, ale existujú aplikácie v mnohých oblastiach ako napríklad rozpoznávaní obrazov, umelej inteligencie a neurónových sietí, kde vedci pri použití výkonných kariet dosiahli urýchlenie oproti CPU 50-100 násobne. Podobné zrýchlenie môžeme vidieť aj v grafe na obrázku č. 2 pri aplikácii detekcií hrán v obraze [7].

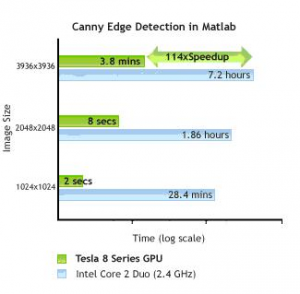
Obr.2: Príklad zrýchlenia detekcie hrán v obraze

Paralelné výpočty na grafickej karte v Matlabe

V období masívneho rozšírenia paralelných výpočtov na GPU firmy ako AccelerEyes a GP-you Group, vyvinuli rozšírenie pre Matlab, ktoré umožňuje priamo v Matlabe používať výkon grafických kariet. Firma AccelerEyes ponúka túto knižnicu pre paralelné výpočty na GPU pod názvom Jacket. Bohužiaľ tento softvér nie je voľne šíriteľný, ale je možnosť po zaregistrovaní si stiahnuť 15 dňovú trial verziu [1, 4]. Naopak firma GP-you Group vyvinula podobnú knižnicu s názvom GPUmat, ktorá podobne ako Jacket umožňuje paralelné výpočty na GPU, ale je voľne šíriteľná (freeware) [2, 5]. Obidve knižnice poskytujú základné funkcie pre výpočty a obsluhu grafickej karty, ktoré majú rovnakú funkciu a líšia sa iba v niekoľkých príkazoch. V prospech knižnice Jacket hovorí existencia ďalších aplikačných nadstavieb ako sú funkcie pre grafiku, neurónových sietí a ďalších demonštračných príkladov. Hlavnou výhodou knižnice GPUmat je voľná dostupnosť pri poskytnutí veľmi dobrého základu pre paralelné výpočty na grafickej karte. Ďalej sa v príspevku budem bližšie zaoberať knižnicou GPUmat.

Knižnica GPUmat je vytvorená tak aby bola jednoducho integrovateľná s Matlabom a existujúce programy sa dali ľahko konvertovať pre beh na GPU. Inštalácia knižnice GPUmat je veľmi jednoduchá stačí ju nakopírovať na určité miesto na disku a spustiť GPUstart.m, program skontroluje kompatibilitu s CUDA rozhraním grafickej karty a pridá cesty do adresárovej štruktúry Matlabu. Pred inštaláciou knižnice GPUmat je potrebné:

• Nainštalovať grafickú kartu s príslušným ovládačom
• Nainštalovať vývojové nástroje CUDA SDK ver. 2.1. alebo 2.2 pre príslušný OS
• Nainštalovať programové vybavenie CUDA Toolkit ver. 2.1. alebo 2.2. pre príslušný OS

Aby sme využívali výpočtový výkon grafickej karty musíme vytvoriť dátovú premennú, ktorá bude umiestnená v pamäti grafickej karty. Takáto premenná musí byť typu single a vytvorí sa pomocou príkazu GPUsingle. Tu sa odhaľuje jedna nevýhoda GPU výpočtov, ktoré dokážu pracovať iba s dátami typu single a nie typu double ako CPU, čím sa znižuje presnosť výpočtu. Keď vytvoríme takúto premennú tak môžeme na ňu aplikovať ľubovoľnú matlabovskú funkciu, pričom sa GPUmat postará o to, aby sa výpočet uskutočnil na grafickej karte. V závislosti od možnosti vykonania tejto funkcie paralelne je operácia spracovaná jednotlivými stream procesormi GPU.

Na príklade násobenia dvoch matíc A, B si vysvetlíme ako výpočet prebieha. Do grafickej pamäte sa zapíšu matice A, B pomocou príkazu GPUsingle. Násobenie matíc A, B je vykonávané tak, že násobenie daného riadku matice A a daného stĺpca matice B je realizované na jednotlivých stream procesoroch GPU a výsledok je zapísaný na danú pozíciu matice C v grafickej pamäti (viď. obr. 3).

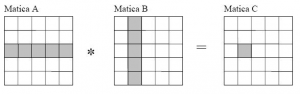
Obr.3: Znázornenie násobenia matíc na GPU

Zápis takejto operácie je nasledovný:

>> A=GPUsingle(rand(100)); % vytvorenie matice A na GPU
>> B=GPUsingle(rand(100)); % vytvorenie matice B na GPU
>> C=A*B;                  % výpočet násobenia matíc na GPU


Podobne sa dajú na GPU vykonať rôzne matematické operácie. Ak chceme dáta z grafickej pamäte preniesť späť do pamäte CPU môžeme použiť príkaz CPUsingle. Výpočet matematických operácií na GPU má dve hlavné nevýhody. Prvou menej závažnou je že nie každá matematická operácia sa dá rovnako dobre paralelne vykonať, čím urýchlenie výpočtu je rôzne a nedá sa presne stanoviť. Druhou závažnejšou nevýhodou je že zrýchlenie výpočtu je závislé od počtu spracovávaných dát, kde zrýchlenie sa začína prejavovať až od vysokého počtu dát, rádovo 1e4 až 1e5. Táto hranica je daná v závislosti od výkonu výpočtového pomeru GPU a CPU a tiež od počtu stream procesorov na GPU.

V nasledovných príkladoch násobenia matíc, násobenia matíc po prvkoch a Fourierovej transformácii na náhodných dátach demonštrujeme možnosti zrýchlenia výpočtov na GPU pomocou knižnice GPUmat. Výpočty boli realizované na dvoch PC s nasledovnými parametrami:

1. PC

CPU AMD Athlon 64 X2 Dual Core Processor 6000+ 3.02 GHz, 2GB RAM
GPU nVidia 8600GT PCX (256MB RAM, 32 stream procesorov)

1. PC

CPU Intel Core 2 Duo E6750 Processor + 2 GHz, 4GB RAM
GPU nVidia GTS250 (512MB RAM, 128 stream procesorov)

Pri testovaní sme sledovali závislosť zrýchlenia výpočtu od počtu spracovávaných dát, kde zrýchlenie výpočtu bolo počítané ako podiel času výpočtu na CPU T_CPU ku času výpočtu na GPU T_GPU. Čas výpočtu T_CPU a T_GPU boli počítané ako štatistický medián z desiatich za sebou spustených výpočtov, čím sa eliminovali náhodné chyby. Výsledky jednotlivých meraní na dvoch rôznych PC sú znázornené na obr. 4 až 6.

Príklad násobenia matíc:

>> A=GPUsingle(rand(100)); % vytvorenie matice A na GPU
>> B=GPUsingle(rand(100)); % vytvorenie matice B na GPU
>> C=A*B;                  % výpočet násobenia matíc na GPU


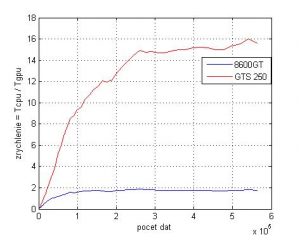
Obr.4: Závislosť zrýchlenia výpočtu maticového násobenia od počtu prvkov matice

Príklad násobenia matíc po prvkoch:

>> A=GPUsingle(rand(100)); % vytvorenie matice A na GPU
>> B=GPUsingle(rand(100)); % vytvorenie matice B na GPU
>> C=A.*B;  % výpočet násobenia matíc po prvkoch na GPU


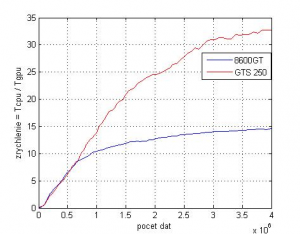
Obr.5: Závislosť zrýchlenia výpočtu maticového násobenia po prvkoch od počtu prvkov matice

Príklad Fourierovej transformácie dát

>> A=GPUsingle(rand(1,1000)); % vytvorenie vektora A na GPU
>> B=GPUsingle(rand(1,1000)); % vytvorenie vektora B na GPU
>> C=A+B;                     % súčet signálov na GPU
>> D=fft(C);                  % výpočet FFT na GPU


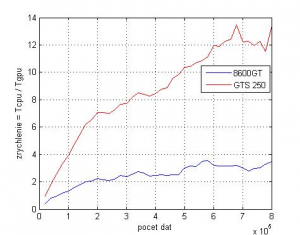
Obr.6: Závislosť zrýchlenia výpočtu Fourierovej transformácie od počtu prvkov vektora

Záver

S existenciou CUDA aplikačného rozhrania pre všeobecné výpočty na grafických kartách rastie počet aplikácií využívajúce paralelné výpočtové možnosti grafických kariet. Vytvorením knižníc ako sú Jacket a GPUmat pre prostredie Matlabu, prináša užívateľom Matlabu možnosť pomerne jednoduchým spôsobom realizovať náročné matematické výpočty na grafickej karte a tým využiť ich paralelné výpočtové možnosti. Meraním na dvoch grafických kartách sme overili, že pomocou knižnice GPUmat (ako aj Jacket) v prostredí Matlab je možné dosiahnuť niekoľkonásobné zrýchlenie (až desiatky) výpočtu matematických operácií. Výhodou paralelných výpočtov na GPU oproti viacjadrovým CPU sú podstatne nižšie finančné náklady. Hlavnou nevýhodou, ako som v príspevku už spomenul je že takýto prístup na zrýchlenie výpočtu sa nedá použiť všeobecne na každú aplikáciu, ale iba na špeciálne aplikácie s veľkým množstvom dát ako sú napr. rozpoznávanie obrazcov, umelá inteligencia, neurónové siete, grafické simulácie, atď.

Literatúra

1. http://www.accelereyes.com – internetová stránka spoločnosti AccelerEyes
2. http://gp-you.org – internetová stránka spoločnosti GP-you
3. http://www.nvidia.com – internetová stránka spoločnosti nVidia
4. The AccelerEyes: Jacket User Guide, jun 2009
5. The GP-you group: GPUmat User Guide, April 2009
6. J. Slačka: Neurónové siete na GPU, seminárna práca z predmetu AVI
7. 7. M. Visconti: Heterogeneous GPU Computing In Computational Science, prezentácia, http://www.osc.edu/supercomputing/training/customize/Mark_Visconti_slides.pdf

---

Spoluautorom článku je J. Slačka, Fakulta elektrotechniky a informatiky STU, Ilkovičova 3, 812 19 Bratislava.