Porovnanie vypočítaných a nameraných parametrov vedení na laboratónom modeli elektrizačnej sústavy

23. December, 2013, Autor článku: Oravský Igor, Elektrotechnika
Ročník 6, číslo 12 Pridať príspevok

p16617_icon Cieľom práce je riešenie problematiky merania a následného porovnania získaných výsledkov s vypočítanými parametrami jednotlivých vedení príslušných napäťových hladín modelu elektrizačnej sústavy, ktorý je umiestnený na Ústave elektroenergetiky a aplikovanej elektrotechniky. Riešenie je rozdelené na teoretickú a praktickú časť.

Cieľom teoretickej časti je výpočet, ktorý vychádza v prvom prípade z pôvodného návrhu modelu a v druhom prípade zo štítkových údajov zariadení namontovaných na danom modeli, t.j. na cievkach predstavujúcich pozdĺžnu impedanciu a kondenzátorov predstavujúcich priečnu admitanciu. Cieľom praktickej časti je meranie vybraných parametrov a ich porovnanie s vypočítanými parametrami. Porovnanie vybraných vypočítaných a nameraných parametrov vedení na laboratórnom modeli elektrizačnej sústavy bude ďalej slúžiť ako špecifikácia elektrických parametrov jednotlivých vedení príslušných napäťových hladín. Praktická analýza v závere poukazuje na dôvody rozdielov medzi vypočítanými a nemeranými parametrami ako aj celkové vyhodnotenie riešenia danej problematiky.

Úvod

Laboratórny model elektrizačnej sústavy je umiestnený na Ústave elektroenergetiky a aplikovanej elektrotechniky. Tento model je určený pre študentov bakalárskeho a inžinierskeho štúdia ako praktická študijná pomôcka v rámci odborných predmetov (napr. Výroba a rozvod elektrickej energie, Elektrické stanice, Elektrické siete, Ustálené stavy), ktoré zastrešuje ÚEAE. Prostredníctvom modelu sa môžu študenti prakticky oboznámiť so skladbou a principiálnym fungovaním elektrizačnej sústavy, ako aj pochopiť niektoré konkrétne javy súvisiace s výrobou, prenosom a rozvodom elektriny. Celý model pozostáva z nasledujúcich 11 samostatných častí – blokov:

generátor
blokový transformátor Tr1 15,75/400kV
rozvodňa RZ1 400kV
vedenie 400kV
rozvodňa RZ2 400kV
transformátor Tr2 400/110kV
vedenie 110kV
transformátor Tr3 110/22kV
rozvodňa 22kV
vedenie 22kV
koniec vedenia 22kV

Bloková schéma vyššie spomenutých blokov modelu ES je zobrazená na Obr. 1.

Obr. 1 Bloková schéma modelu ES

1. Výpočet parametrov náhradných článkov

V tejto časti je uvedený popis a výpočet parametrov náhradných článkov vedení príslušných napäťových hladín, ktoré sú reprezentované nasledovnými blokmi modelu:

Blok 4 – vedenie 400 kV
Blok 7 – vedenie 110 kV
Blok 10 – vedenie 22 kV

Výpočet parametrov jednotlivých vedení bol realizovaný na základe údajov vychádzajúcich z návrhu modelu a na základe štítkových údajov uvedených na cievkach predstavujúcich pozdĺžnu impedanciu a kondenzátorov predstavujúcich priečnu admitanciu. Je predpoklad, že výpočet na základe štítkových údajov sa bude reálnemu stavu približovať najviac, pretože sú to prvky, ktoré model reálne obsahuje. Na záver tejto časti sú vypočítané parametre zhrnuté do sumárnych tabuliek pre väčšiu prehľadnosť. Tieto vypočítané hodnoty budú v ďalšej časti porovnávané s nameranými hodnotami. Z dôvodu, že sa jedná o symetrické vedenie sú vypočítané veľkosti jednotlivých impedancií a admitancií pre jednotlivé fázy príslušných vedení rovnaké.

1.1 Výpočet parametrov pre vedenie 400 kV vychádzajúci zo štítkových údajov

Konštrukcia modelu pre vedenie 400 kV, skladajúca sa z Steinmetzovho článku, je znázornená na Obr. 2.

Obr. 2 Náhradná schéma pre model 400 kV vedenia – Steinmetzov článok

Elektrické parametre pre toto usporiadanie vychádzajúce zo štítkových údajov sa nachádzajú v Tab.1.

Tab. 1 Elektrické parametre vychádzajúce zo štítkových údajov pre vedenie 400 kV

R [Ω/km]	0,02
L [mH/km]	0,916
C [nF/km]	13,2
l [km]	2×150 (dvojité vzdušné vedenie)

Pre impedanciu jednej fázy vedenia 400 kV platí :

$\overline{Z}_c = l(R+j\omega L) = 150(0,02+j\omega 0,916.10^{-3})=$

$=3+j\omega 0,1374 = 3+j43,165=43,269 \angle 86,02^o \Omega$

(1.1)

Pre admitanciu jednej fázy vedenia 22 kV platí :

$\overline{Y}_c=lj \omega C=150j \omega 13,2.10^{-9} = j \omega 1,98.10^{-6} =$

$= 622,035.10^{-6} \angle 90^{o} S$

(1.2)

Potom pre prvky Steinmetzovho náhradného článku platí:

$\overline{Z}_{1/2}={\overline{Z}_c}{2}=21,634 \angle 86,02^o \Omega$

(1.3)

$\overline{Y}_{1/6}=\frac{\overline{Y}_c}{6}=103,672.10^{-6} \angle 90^o S$

(1.4)

$R=\frac{3}{2}=1,5 \Omega$

(1.5)

$L=\frac{0,1374}{2}=0,0687 H$

(1.6)

$C= \frac{1,98.10^{-6}}{6}=330 nF$

(1.7)

1.2 Výpočet parametrov pre vedenie 400 kV vychádzajúci z návrhu

Elektrické parametre pre vedenie napäťovej hladiny 400 kV, vychádzajúce z údajov návrhu, sú uvedené v Tab. 2.

Tab. 2 Elektrické parametre vychádzajúce z údajov návrhu pre vedenie 400 kV

R [Ω/km]	0,0215
L [mH/km]	0,916
C [nF/km]	12,5
l [km]	2×150 (dvojité vzdušné vedenie)

Pre impedanciu jednej fázy vedenia 400 kV platí :

$\overline{Z}_c = l(R+j\omega L) = 150(0,0215+j\omega 0,916.10^{-3})=$

$=3,225+j\omega 0,1374 = 3,225+j43,165=43,285 \angle 85,72^o \Omega$

(1.8)

Pre admitanciu jednej fázy vedenia 22 kV platí :

$\overline{Y}_c=lj \omega C=150j \omega 12,5.10^{-9} = j \omega 1,875.10^{-6} =$

$= 589,048.10^{-6} \angle 90^{o} S$

(1.9)

Potom pre prvky Steinmetzovho náhradného článku platí:

$\overline{Z}_{1/2}={\overline{Z}_c}{2}=21,642 \angle 86,02^o \Omega$

(1.10)

$\overline{Y}_{1/6}=\frac{\overline{Y}_c}{6}=98,174.10^{-6} \angle 90^o S$

(1.11)

$R=\frac{3,225}{2}=1,6125 \Omega$

(1.12)

$L=\frac{0,1374}{2}=0,0687 H$

(1.13)

$C= \frac{1,875.10^{-6}}{6}=312,5 nF$

(1.14)

1.3 Výpočet parametrov pre vedenie 110 kV vychádzajúci zo štítkových údajov

Konštrukcia modelu pre vedenie 110 kV, skladajúca sa z dvoch do série zapojených gama článkov, je znázornená na Obr. 3.

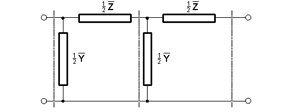
Obr. 3 Náhradná schéma pre model 110 kV vedenia pozostávajúci z dvoch sériovo zapojených Gama článkov

Elektrické parametre pre toto usporiadanie vychádzajúce zo štítkových údajov sa nachádzajú v Tab.1.

Tab. 3 Elektrické parametre vychádzajúce zo štítkových údajov pre vedenie 110 kV

R [Ω/km]	0,140
L [mH/km]	1,295
C [nF/km]	8,4
l [km]	40 (vzdušné vedenie)

Pre impedanciu jednej fázy vedenia 110 kV platí:

$\overline{Z}_c = l(R+j\omega L) = 40(0,140+j\omega 1,295.10^{-3})=$

$=5,6+j\omega 0,518 = 5,6+j16,273=17,2 \angle 71^o \Omega$

(1.15)

Pre admitanciu jednej fázy vedenia 110 kV platí:

$\overline{Y}_c=lj \omega C=40j \omega 8,4.10^{-9} = j \omega 3,36.10^{-7} =$

$= 105,557.10^{-6} \angle 90^{o} S$

(1.16)

Potom pre jeden gama článok platí:

$\overline{Z}_{1/2}={\overline{Z}_c}{2}=8,6 \angle 71^o \Omega$

(1.17)

$\overline{Y}_{1/2}=\frac{\overline{Y}_c}{2}=52,778.10^{-6} \angle 90^o S$

(1.18)

$R=\frac{5,6}{2}=2,8 \Omega$

(1.19)

$L=\frac{0,0518}{2}=0,0259 H$

(1.20)

$C= \frac{3,36.10^{-7}}{2}=168 nF$

(1.21)

1.4 Výpočet parametrov pre vedenie 110 kV vychádzajúci z návrhu

Elektrické parametre pre vedenie napäťovej hladiny 110 kV, vychádzajúce z údajov návrhu, sú uvedené v Tab. 4.

Tab. 4 Elektrické parametre vychádzajúce z údajov návrhu pre vedenie 110 kV

R [Ω/km]	0,156
L [mH/km]	1,295
C [nF/km]	8,9
l [km]	40 (vzdušné vedenie)

Pre impedanciu jednej fázy vedenia 110 kV platí:

$\overline{Z}_c = l(R+j\omega L) = 40(0,156+j\omega 1,295.10^{-3})=$

$=6,24+j\omega 0,0518 = 6,24+j16,273=17,42 \angle 69,02^o \Omega$

(1.22)

Pre admitanciu jednej fázy vedenia 110 kV platí:

$\overline{Y}_c=lj \omega C=40j \omega 8,9.10^{-9} = j \omega 3,56.10^{-7} =$

$= 111,8.10^{-6} \angle 90^{o} S$

(1.23)

Potom pre jeden gama článok platí:

$\overline{Z}_{1/2}={\overline{Z}_c}{2}=8,71 \angle 71^o \Omega$

(1.24)

$\overline{Y}_{1/2}=\frac{\overline{Y}_c}{2}=55,9.10^{-6} \angle 90^o S$

(1.25)

$R=\frac{6,24}{2}=3,12 \Omega$

(1.26)

$L=\frac{0,0518}{2}=0,0259 H$

(1.27)

$C= \frac{3,56.10^{-7}}{2}=178 nF$

(1.28)

1.5 Výpočet parametrov pre vedenie 22 kV vychádzajúci zo štítkových údajov

Konštrukcia modelu pre vedenie 22 kV, skladajúca sa zo štyroch do série zapojených gama článkov, je znázornená na Obr. 4.

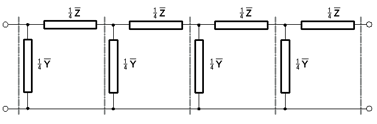
Obr. 4 Náhradná schéma pre model 22 kV vedenia pozostávajúci zo štyroch sériovo zapojených Gama článkov

Elektrické parametre pre toto usporiadanie, vychádzajúce zo štítkových údajov, sa nachádzajú v Tab.5.

Tab. 5 Elektrické parametre vychádzajúce zo štítkových údajov pre vedenie 22 kV

R [Ω/km]	0,28
L [mH/km]	2,2
C [nF/km]	9,4
l [km]	2×20 (dvojité vzdušné vedenie)

Pre impedanciu jednej fázy vedenia 22 kV platí:

$\overline{Z}_c = l(R+j\omega L) = 20(0,28+j\omega 2,2.10^{-3})=$

$=5,6+j\omega 0,044 = 5,6+j13,823=14,914 \angle 67,94^o \Omega$

(1.29)

Pre admitanciu jednej fázy vedenia 22 kV platí:

$\overline{Y}_c=lj \omega C=20j \omega 9,4.10^{-9} = j \omega 1,88.10^{-7} =$

$= 622,035.10^{-6} \angle 90^{o} S$

(1.30)

Potom pre jeden gama článok platí:

$\overline{Z}_{1/4}={\overline{Z}_c}{4}=3,727 \angle 67,94^o \Omega$

(1.31)

$\overline{Y}_{1/4}=\frac{\overline{Y}_c}{4}=14,765.10^{-6} \angle 90^o S$

(1.32)

$R=\frac{5,6}{4}=1,4 \Omega$

(1.33)

$L=\frac{0,044}{4}=0,011 H$

(1.34)

$C= \frac{1,88.10^{-7}}{4}=47 nF$

(1.35)

1.6 Výpočet parametrov pre vedenie 22 kV vychádzajúci z návrhu

Elektrické parametre pre vedenie napäťovej hladiny 22 kV, vychádzajúce z údajov návrhu, sú uvedené v Tab. 6.

Tab. 6 Elektrické parametre vychádzajúce z údajov návrhu pre vedenie 22 kV

R [Ω/km]	0,5
L [mH/km]	1,01
C [nF/km]	10,2
l [km]	2×20 (dvojité vzdušné vedenie)

Pre impedanciu jednej fázy vedenia 22 kV platí:

$\overline{Z}_c = l(R+j\omega L) = 20(0,5+j\omega 1,01.10^{-3})=$

$=10+j\omega 0,0202 = 10+j6,346=11,843 \angle 32,39^o \Omega$

(1.36)

Pre admitanciu jednej fázy vedenia 22 kV platí:

$\overline{Y}_c=lj \omega C=20j \omega 10,2.10^{-9} = j \omega 2,04.10^{-7} =$

$= 64,088.10^{-6} \angle 90^{o} S$

(1.37)

Potom pre jeden gama článok platí:

$\overline{Z}_{1/4}={\overline{Z}_c}{4}=2,960 \angle 32,39^o \Omega$

(1.38)

$\overline{Y}_{1/4}=\frac{\overline{Y}_c}{4}=16,022.10^{-6} \angle 90^o S$

(1.39)

$R=\frac{10}{4}=2,5 \Omega$

(1.40)

$L=\frac{0,0202}{4}=0,0505 H$

(1.41)

$C= \frac{0,04.10^{-7}}{4}=51 nF$

(1.42)

Tab. 7 Sumár veľkostí vypočítaných veličín vychádzajúcich zo štítkových údajov

	Vedenie 400 kV		Vedenie 110 kV		Vedenie 22 kV
Fáza	Z_C [Ω]	Y_C [μS]	Z_C [Ω]	Y_C [μS]	Z_C [Ω]	Y_C [μS]
L1	43,269	622,035	17,200	105,557	14,914	59,061
L2	43,269	622,035	17,200	105,557	14,914	59,061
L3	43,269	622,035	17,200	105,557	14,914	59,061

Tab. 8 Sumár veľkostí vypočítaných veličín vychádzajúcich z návrhu

	Vedenie 400 kV		Vedenie 110 kV		Vedenie 22 kV
Fáza	Z_C [Ω]	Y_C [μS]	Z_C [Ω]	Y_C [μS]	Z_C [Ω]	Y_C [μS]
L1	43,285	589,048	17,420	111,800	11,843	64,088
L2	43,285	589,048	17,420	111,800	11,843	64,088
L3	43,285	589,048	17,420	111,800	11,843	64,088

2. Namerané parametre náhradných článkov vedení

Táto časť obsahuje namerané elektrické veličiny (napätia, prúdy) pre vybrané prvky modelu ES, konkrétne pre vedenia 400 kV, 110 kV a 22 kV. Na základe merania boli následne opäť vypočítané elektrické parametre pre príslušné vedenia s cieľom ich porovnania s vypočítanými hodnotami parametrov zo štítkových údajov zariadení. Súčasťou tejto časti práce sú okrem vypočítaných parametrov a nameraných veličín tiež vzorové výpočty a názorné grafické zobrazenie signálu, ktorý bol vyhodnocovaný. Meranie veličín bolo realizované pomocou analyzátoru BK – ElCOM. Parametre jednotlivých fáz príslušných vedení boli vypočítané prostredníctvom programu Wolfram Mathematica. Grafické vyhodnotenie z analyzátora bolo spracované pomocou programu na analýzu nameraných dát BK – Report.

Vysvetlivky k označeniam veličín v tabuľkách

Pre tabuľky nameraných prúdov a napätí:

U_f1 – veľkosť fázového napätia na začiatku vedenia
U_f2 – veľkosť fázového napätia na konci vedenia
I₁ – veľkosť fázového prúdu na začiatku vedenia
I₂ – veľkosť fázového prúdu na konci vedenia
φ₁ – fázorový uhol na začiatku vedenia
φ₂ – fázorový uhol na konci vedenia

Pre tabuľky nameraných výkonov:

S₁ – veľkosť zdanlivého výkonu jednej fázy na začiatku vedenia
S₂ – veľkosť zdanlivého výkonu jednej fázy na konci vedenia
P₁ – veľkosť činného výkonu jednej fázy na začiatku vedenia
P₂ – veľkosť činného výkonu jednej fázy na konci vedenia
Q₁ – veľkosť jalového výkonu jednej fázy na začiatku vedenia
Q₂ – veľkosť jalového výkonu jednej fázy na konci vedenia
φ₁ – fázorový uhol na začiatku vedenia
φ₂ – fázorový uhol na konci vedenia

2.1 Namerané parametre pre vedenie 400 kV

Tab. 9 Namerané prúdy a napätia pre vedenie 400 kV

	Začiatok vedenia				Koniec vedenia
Fáza	U_f1 [V]	φ₁ [°]	I₁ [A]	φ₁ [°]	U_f2 [V]	φ₂ [°]	I₂ [A]	φ₂ [°]
L1	239,943	0,000	214,403	24,709	2,184	21,560	2,185	24,258
L2	240,179	0,000	212,633	24,821	2,173	21,775	2,201	24,446
L3	241,249	0,000	221,714	23,184	2,081	19,930	2,080	22,340

Tab. 10 Namerané výkony pre vedenie 400 kV

	Začiatok vedenia				Koniec vedenia
Fáza	S₁ [VA]	φ₁ [°]	P₁ [W]	Q₁ [var]	S₂ [VA]	φ₂ [°]	P₂ [W]	Q₂ [var]
L1	524,018	21,560	487,354	192,563	468,367	48,967	307,483	353,302
L2	522,088	21,775	484,836	193,676	467,937	49,267	305,347	354,582
L3	502,080	19,930	472,009	171,148	461,111	45,524	323,059	329,023

Vzorový výpočet výkonov pre fázu L1 sa nachádza v Prílohe č.1. Na základe všeobecnej teórie o štvorpóloch v maticovom tvare (2.1) možno pre Steinmetzov náhradný článok ďalej odvodiť vzťahy 2.2 a 2.3.

$\left[ \begin{array}{c} \overline{U}_{f1} \\ \overline{I}_1 \end{array} \right] = \left[ \begin{array}{cc} \overline{A} & \overline{B} \\ \overline{C} & \overline{D} \end{array} \right] \left[ \begin{array}{c} \overline{U}_{f2} \\ \overline{I}_2 \end{array} \right]$

(2.1)

$\overline{I}_1= \overline{U}_{f2} \left ( \overline{Y} \left ( 1+ \frac{5\overline{Z} \overline{Y}}{36}+\frac{\overline{Z}^2 \overline{Y}^2}{216} \right ) \right ) + \overline{I}_2 \left (1+ \frac{\overline{Z} \overline{Y}}{2} +\frac{\overline{Z}^2 \overline{Y}^2}{36} \right )$

(2.2)

$\overline{U}_{f1}=\overline{U}_{f2} \left ( 1+ \frac{ \overline{Z} \overline{Y}}{2}+\frac{\overline{Z}^2 \overline{Y}^2}{36} \right ) +\overline{I}_2 \left ( \overline{Z} \left ( 1+ \frac{\overline{Z} \overline{Y}}{6} \right ) \right )$

(2.3)

Ako vyjadrenie parametrov zo vzťahov 2.2 a 2.3, tak aj vzorový výpočet pre fázu L1 sa nachádza v Prílohe č.2. Názorné grafické zobrazenie signálu v čase sa nachádza v Prílohe č.3.

	Vedenie 400 kV
Fáza	Z_C [Ω]	Y_C [μS]
L1	45,882	462,835
L2	46,089	476,064
L3	45,598	385,159

2.2 Namerané parametre pre vedenie 110 kV

Tab. 12 Namerané prúdy a napätia pre vedenie 110 kV

	Začiatok vedenia				Koniec vedenia
Fáza	U_f1 [V]	φ₁ [°]	I₁ [A]	φ₁ [°]	U_f2 [V]	φ₂ [°]	I₂ [A]	φ₂ [°]
L1	76,228	0,000	69,563	11,024	0,715	10,469	0,705	10,522
L2	75,948	0,000	69,292	10,432	0,713	10,321	0,707	9,775
L3	76,112	0,000	70,131	10,011	0,654	9,638	0,654	8,998

Tab. 13 Namerané výkony pre vedenie 110 kV

	Začiatok vedenia				Koniec vedenia
Fáza	S₁ [VA]	φ₁ [°]	P₁ [W]	Q₁ [var]	S₂ [VA]	φ₂ [°]	P₂ [W]	Q₂ [var]
L1	54,470	10,890	53,563	9,897	49,060	21,546	45,632	18,017
L2	54,130	10,050	53,254	9,698	48,979	20,207	45,965	16,918
L3	49,763	9,638	49,061	8,331	45,851	19,009	43,351	14,934

Vzorový výpočet výkonov pre fázu L2 sa nachádza v Prílohe č.1. Pre náhradný Gama článok na základe vzťahu maticového zápisu pre štvorpól (2.1) je možné napísať nasledovné odvodené vzťahy:

$\overline{I}_1= \overline{U}_{f2} \overline{Y}+\overline{I}_2 (1+\overline{Z} \overline{Y})$

(2.4)

$\overline{U}_{f1}=\overline{U}_{f2}+\overline{I}_2 \overline{Z}$

(2.5)

Vyjadrenie elektrických parametrov vychádzajúci zo vzťahov 2.4 a 2.5 ako aj vzorový výpočet pre fázu L2 sa nachádza v Prílohe č.2. Názorné grafické zobrazenie signálu v čase sa nachádza v Prílohe č.3.

Tab. 14 Namerané elektrické parametre pre vedenie 110 kV

	Vedenie 110 kV
Fáza	Z_C [Ω]	Y_C [μS]
L1	21,980	131,468
L2	20,900	117,332
L3	21,539	95,950

2.3 Namerané parametre pre vedenie 22 kV

Tab. 15 Namerané napätia a prúdy pre vedenie 22 kV

	Začiatok vedenia				Koniec vedenia
Fáza	U_f1 [V]	φ₁ [°]	I₁ [A]	φ₁ [°]	U_f2 [V]	φ₂ [°]	I₂ [A]	φ₂ [°]
L1	141,437	0,000	137,271	5,886	1,415	5,875	1,390	5,336
L2	140,702	0,000	136,584	5,556	1,413	5,528	1,408	7,569
L3	148,207	0,000	144,261	5,246	1,361	5,115	1,343	4,554

Tab. 16 Namerané výkony pre vedenie 22 kV

	Začiatok vedenia				Koniec vedenia
Fáza	S₁ [VA]	φ₁ [°]	P₁ [W]	Q₁ [var]	S₂ [VA]	φ₂ [°]	P₂ [W]	Q₂ [var]
L1	200,075	5,490	199,024	20,479	190,817	11,222	187,169	37,135
L2	198,809	5,528	197,884	19,152	192,323	13,125	187,299	43,670
L3	201,782	5,115	200,978	17,992	193,788	9,800	190,960	32,984

Vzorový výpočet výkonov pre fázu L3 sa nachádza v Prílohe č.1. Pre vedenie 22 kV platia tie isté odvodené vzťahy aj vyjadrenia elektrických parametrov ako pri predošlom vedení. Vzorový výpočet pre fázu L3 sa nachádza v Prílohe č.2. Názorné grafické zobrazenie signálu v čase sa nachádza v Prílohe č.3.

Tab. 17 Namerané elektrické parametre pre vedenie 22 kV

	Vedenie 22 kV
Fáza	Z_C [Ω]	Y_C [μS]
L1	10,721	198,990
L2	9,982	358,847
L3	10,387	151,929

3. Porovnanie vypočítaných a nameraných parametrov náhradných článkov vedení

Porovnanie vybraných vypočítaných a nameraných elektrických parametrov modelu ES sa nachádza v nasledujúcich porovnávacích tabuľkách. V porovnaní sú okrem nameraných a vypočítaných hodnôt uvedené aj rozdiely medzi jednotlivými fázami prostredníctvom absolútnej a relatívnej chyby.

Vysvetlivky k označeniam veličín v tabuľkách

Pre porovnávacie tabuľky impedancií:

Z_CS – veľkosť celkovej impedancie vychádzajúcej zo štítkových údajov
Z_CN – veľkosť celkovej impedancie vychádzajúcej z nameraných hodnôt
Z_CNA – veľkosť celkovej impedancie vychádzajúcej z návrhu
|∆Z| – absolútna hodnota rozdielu impedancií
δ_Z – relatívna chyba pre impedancie

Pre porovnávacie tabuľky admitancií:

Y_CS – veľkosť celkovej admitancie vychádzajúcej zo štítkových údajov
Y_CN – veľkosť celkovej admitancie vychádzajúcej z nameraných hodnôt
Y_CNA – veľkosť celkovej admitancie vychádzajúcej z návrhu
|∆Y| – absolútna hodnota rozdielu admitancií
δ_Y – relatívna chyba pre admitancie

3.1 Porovnanie vypočítaných a nameraných elektrických parametrov pre vedenie 400 kV

Tab. 18 Porovnanie nameranej impedancie s teoretickým výpočtom vedenia 400 kV

	Porovnanie so štítkovými údajmi				Porovnanie s návrhom
Fáza	Z_CS [Ω]	Z_CN [Ω]	\|∆Z\|[Ω]	δ_Z [%]	Z_CNA [Ω]	Z_CN [Ω]	\|∆Z\|[Ω]	δ_Z [%]
L1	43,269	45,882	2,613	6,039	43,285	45,882	2,597	6,000
L2	43,269	46,089	2,820	6,517	43,285	46,089	2,804	6,478
L3	43,269	45,598	2,329	5,382	43,285	45,598	2,313	5,343

Vzorový výpočet pre |∆Z|:

$|\Delta Z|=|Z_{CN}-Z_{CS}|=|45,882-43,269|=2,613 \Omega$

(3.1)

Vzorový výpočet pre |∆Y|:

$\delta_Z=\frac{|\Delta Z|}{Z_{CS}} 100=\frac{|45,882-43,269|}{43,269} 100=6,039%$

(3.2)

	Porovnanie so štítkovými údajmi				Porovnanie s návrhom
Fáza	Y_CS [μS]	Y_CN [μS]	\|∆Y\|[μS]	δ_Y [%]	Y_CNA [μS]	Y_CN [μS]	\|∆Y\|[μS]	δ_Y [%]
L1	622,035	462,835	159,200	25,593	589,048	462,835	126,213	21,427
L2	622,035	476,064	145,971	23,467	589,048	476,064	112,984	19,181
L3	622,035	385,159	236,876	38,081	589,048	385,159	203,889	34,613

Vzorový výpočet pre δ_Y:

$|\Delta Y|=|Y_{CN}-Y_{CS}|=|462,835-622,035|=159,20 \mu S$

(3.3)

Vzorový výpočet pre δ_Z:

$\delta_Y=\frac{|\Delta Y|}{Y_{CS}} 100= \frac{|462,835-622,035|}{622,035} 100=25,593%$

(3.4)

3.2 Porovnanie vypočítaných a nameraných elektrických parametrov pre vedenie 110kV

Tab. 20 Porovnanie nameranej impedancie s teoretickým výpočtom vedenia 110 kV

	Porovnanie so štítkovými údajmi				Porovnanie s návrhom
Fáza	Z_CS [Ω]	Z_CN [Ω]	\|∆Z\|[Ω]	δ_Z [%]	Z_CNA [Ω]	Z_CN [Ω]	\|∆Z\|[Ω]	δ_Z [%]
L1	17,200	21,980	4,780	27,790	17,420	21,980	4,560	26,176
L2	17,200	20,900	3,700	21,512	17,420	20,900	3,480	19,977
L3	17,200	21,539	4,339	25,227	17,420	21,539	4,119	23,645

Vzorový výpočet pre |∆Z|:

$|\Delta Z|=|Z_{CN}-Z_{CS}|=|21,980-17,200|=4,780 \Omega$

(3.5)

Vzorový výpočet pre |∆Y|:

$\delta_Z=\frac{|\Delta Z|}{Z_{CS}} 100=\frac{|21,980-17,200|}{17,200} 100=27,790%$

(3.6)

	Porovnanie so štítkovými údajmi				Porovnanie s návrhom
Fáza	Y_CS [μS]	Y_CN [μS]	\|∆Y\|[μS]	δ_Y [%]	Y_CNA [μS]	Y_CN [μS]	\|∆Y\|[μS]	δ_Y [%]
L1	105,557	131,468	25,911	24,547	111,8	131,468	19,668	17,592
L2	105,557	117,332	11,775	11,155	111,8	117,332	5,532	4,948
L3	105,557	95,950	9,607	9,101	111,8	95,950	15,850	14,177

Vzorový výpočet pre δ_Y:

$|\Delta Y|=|Y_{CN}-Y_{CS}|=|131,468-105,557|=25,911 \mu S$

(3.7)

Vzorový výpočet pre δ_Z:

$\delta_Y=\frac{|\Delta Y|}{Y_{CS}} 100= \frac{|131,468-105,557|}{105,557} 100=24,547%$

(3.8)

3.3 Porovnanie vypočítaných a nameraných elektrických parametrov pre vedenie 22 kV

Tab. 22 Porovnanie nameranej impedancie s teoretickým výpočtom vedenia 22 kV

	Porovnanie so štítkovými údajmi				Porovnanie s návrhom
Fáza	Z_CS [Ω]	Z_CN [Ω]	\|∆Z\|[Ω]	δ_Z [%]	Z_CNA [Ω]	Z_CN [Ω]	\|∆Z\|[Ω]	δ_Z [%]
L1	14,914	10,721	4,193	28,115	11,843	10,721	1,122	9,474
L2	14,914	9,982	4,932	33,071	11,843	9,982	1,861	15,716
L3	14,914	10,387	4,527	30,354	11,843	10,387	1,456	12,294

Vzorový výpočet pre |∆Z|:

$|\Delta Z|=|Z_{CN}-Z_{CS}|=|10,721-14,914|=4,193 \Omega$

(3.9)

Vzorový výpočet pre |∆Y|:

$\delta_Z=\frac{|\Delta Z|}{Z_{CS}} 100=\frac{|10,721-14,914|}{14,914} 100=28,115%$

(3.10)

Tab. 23 Porovnanie nameranej admitancie s teoretickým výpočtom vedenia 22 kV

	Porovnanie so štítkovými údajmi				Porovnanie s návrhom
Fáza	Y_CS [μS]	Y_CN [μS]	\|∆Y\|[μS]	δ_Y [%]	Y_CNA [μS]	Y_CN [μS]	\|∆Y\|[μS]	δ_Y [%]
L1	59,061	198,990	139,929	236,923	64,088	198,990	134,902	210,495
L2	59,061	358,847	299,786	507,587	64,088	358,847	294,759	459,929
L3	59,061	151,929	92,868	157,241	64,088	151,929	87,841	137,063

Vzorový výpočet pre δ_Y:

$|\Delta Y|=|Y_{CN}-Y_{CS}|=|198,990-59,061|=139,929 \mu S$

(3.11)

Vzorový výpočet pre δ_Z:

$\delta_Y=\frac{|\Delta Y|}{Y_{CS}} 100= \frac{|198,990-59,061|}{59,061} 100=236,923%$

(3.12)

4. Záver

V teoretickej analýze parametrov sa predpokladalo, že parametre vypočítané zo štítkových údajov sa budú reálnemu stavu približovať najviac. Na základe získaných výsledkov práce je možné konštatovať, že predpoklad uvedený v teoretickej analýze sa nepotvrdil. V porovnávacích tabuľkách je jednoznačne vidieť, tak ako pri absolútnych, tak aj relatívnych chybách, že teoretické výpočty vychádzajúce z návrhu sú presnejšie. Avšak správnosť predpokladu mohli ovplyvniť viaceré faktory. Jedným z nich je presnosť, respektíve relevantnosť teoretického výpočtu vychádzajúceho zo štítkových údajov. Výsledok tohto výpočtu mohla skresliť tolerancia hodnôt parametrov udávaná výrobcom na použitých súčiastkach predstavujúcich impedanciu a admitanciu. Ďalším faktorom vnášajúcim možnú chybu mohlo byť samotné meranie.

Meranie bolo realizované pri prevádzke modelu a skúmaný signál bol skreslený prechodom predošlými blokmi modelu ES. Skreslenie je možné vidieť v jednotlivých prílohách tohto príspevku pre jednotlivé vedenia, pričom vplyv predmetného skreslenia sa zväčšovalo s narastajúcou vzdialenosťou merania od generátora. To znamená, že pri vedení 22 kV sú chyby nepresnosti výpočtov najvyššie. Pre odstránenie skreslenia signálu by bolo potrebné meranie jednotlivých vedení realizovať použitím napájania 3-f zdrojom. V niektorých prípadoch by bolo tiež vhodné samotný meraný signál rozdeliť na jednotlivé harmonické zložky a až potom vyhodnocovať jednotlivé merania.

Na základe meraní je ďalej možné konštatovať, že modely vedení sú z pohľadu parametrov vo veľkej miere nesymetrické. Pretože impedancie aj admitancie jednotlivých fáz daného vedenia sa v niektorých prípadoch veľkostne odlišujú. V tomto smere možno za najsymetrickejšie vedenie považovať 400 kV vedenie. Je to pravdepodobne spôsobené tým, že model vedenia 400 kV pozostáva zo Steimetzovho náhradného článku, ktorý je spomedzi použitých článkov najpresnejší. Ďalším dôvodom symetrickosti by mohla byť už spomínaná skreslenosť meraného signálu, ktorá bola najnižšia práve pri tomto modeli vedenia. Záverom príspevku je vhodné doplniť, že problematika modelu ES nie je definitívne vyriešená, a preto tu existuje priestor pre doplňujúce analýzy.

Prílohy

Prílohy

Spoluautormi článku sú Boris Cintula, Vladimír Volčko, Peter Janiga, Ústav elektroenergetiky a aplikovanej elektrotechniky FEI STU, Oddelenie elektroenergetiky, Ilkovičova 3, 812 19 Bratislava 1.

O časopise

Meta

RSS

Porovnanie vypočítaných a nameraných parametrov vedení na laboratónom modeli elektrizačnej sústavy

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív