This paper deals with of inset permanent magnet synchronous motor with distributed winding on the stator. This paper describes the separation of synchronous motors and rotor configurations. Using the Finite Element Method Magnetics (FEMM) shows the magnetic fields of inset permanent magnet synchronous motor with distributed winding on the stator in no-load condition, in loaded condition and in the condition armature reaction.

Introduction

Synchronous motors using on the excitation permanent magnets and thereby is removed the commutation problem (wear brushes dc motors). Using of type and volume of permanent magnet influences operational properties of synchronous motors with distributed winding. For this reason it is important examine properties of permanent magnets in term of magnetic fields.

1. Separation and rotor configurations of synchronous motors

Synchronous machine can operate as a:

• generator – alternators (the magnetic field is drawn rotor),
• motor (rotor is drawn the magnetic field),
• compensator (not to subscribe not even not to supply active power but works in order to supply reactive power into network) [1].

Synchronous motors are used in applications where with change the load don´t change the speed for example drive fans. Synchronous motors operate at a constant speed in absolute synchronism with the line frequency. Synchronous motors are classified according to their rotors design, construction, materials and operation into the four basic groups:

• electromagnetically excited motors,
• PM motors,
• reluctance motors,
• hysteresis motors.

Permanent magnet synchronous motors are usually built with one of the following rotor configurations:

• classical (with salient poles, laminated pole shoes and a cage winding) (Fig. 1a),
• interior magnet rotor (Fig. 1b),
• surface magnet rotor (Fig. 1c),
• inset magnet rotor (Fig. 1d),
• rotor with buried magnets symmetrically distributed (Fig. 1e),
• rotor with buried magnets asymmetrically distributed (Fig. 1f) [2].

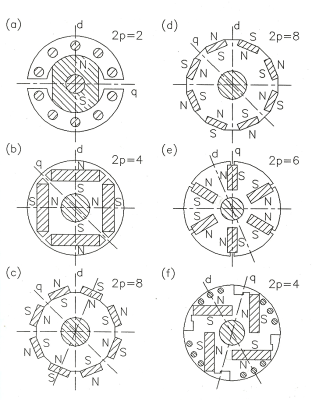
Fig. 1 Rotor configurations for permanent magnet synchronous motor

2. Finite Element Method

Finite element method is a computer method on solution problems in field theory (strength, deformation, electrostatic, electromagnetic, temperature, speed, etc.). Finite element method is an approximate method of solving a system of partial differential equations (differential equations of heat conduction, electric current, electromagnetic induction, etc.). It is ranked among the most versatile, most advanced and most efficient numerical methods for solving the problems temperature field, electromagnetic field etc. The basic difference finite element method compared to other numerical methods is that the replacement functions are chosen not for the whole investigated area but for the subarea final dimensions – finite elements. There finite elements are shaped line, area or volume finite dimensions [3].

3. The software program finite element method magnetics (FEMM)

Magnetic fields are solved using the program Finite Element Method Magnetics (FEMM) in of inset ferrite permanent magnets synchronous motor with distributed winding on the stator. FEMM is a set programs on solve static and low frequency magnetic fields. These programs usually solve problems in two dimensional and axial symmetrical environment. The program FEMM currently addresses linear (nonlinear) magnetostatic problems, linear (nonlinear) time harmonic magnetic problems, linear electrostatic problems, and steady-state heat flow problems. The program FEMM is divided into three parts:

• femm.exe (This program is a multiple document interface pre-processor and a post-processor for the various types of problems solved by FEMM. It contains a CAD like interface for laying out the geometry of the problem to be solved and for defining material properties and boundary conditions. AutoCAD .dxf files can be imported to facilitate the analysis of existing geometries. Field solutions can be displayed in the form of contour and density plots. The program also allows the user to inspect the field at arbitrary points, as well as evaluate a number of different integrals and plot various quantities of interest along user defined contours.),
• triangle.exe (Triangle breaks down the solution region into a large number of triangles, what is a vital part of the finite element method.),
• solvers (Each solver takes a set of data files that describe problem and solves the relevant partial differential equations to obtain values for the desired field throughout the solution domain.):
  • fkern.exe (for magnetics problems),
  • belasolv (for electrostatics problems),
  • fsolv (for heat flow problems),
  • csolv (for current flow problems).

For the use the finite element method it is important to define the boundary conditions to ensure unique solutions. Boundary conditions in the program FEMM for magnetic problems are the following:

• Dirichlet boundary conditions (magnetic field lines do not exceed a border investigated area),
• Neumann boundary conditions (magnetic field lines exceed a border investigated area at angle 90 °),
• Robin boundary conditions (this boundary condition is an amalgamation of two previous, used in special cases),
• Periodic boundary conditions (joins two boundaries together, where the boundary values on corresponding points of the two boundaries are set equal to one another),
• Antiperiodic boundary conditions (also joins together two boundaries, however the boundary values are made to be of equal magnitude but opposite sign) [4].

3.1 Magnetostatic problems in the program FEMM

According to the theory of magnetic field and [4] can for magnetostatic analysis we write:

(1)

(2)

where H is the intensity of the magnetic field, B is the magnetic flux density and J is current density. From equations (1) and (2) is seen that magnetostatic analysis is analysis in which the fields are time-invariant. Relationship between the magnetic flux density B and the intensity of the magnetic field H for each material is:

(3)

where μ is the permeability.

4 The magnetic fields of inset permanent magnet synchronous motor with distributed winding on the stator

Basic parameters investigated of synchronous motor which are the basis for solving the magnetic fields are as follows:

• P = 100 W – nominal power,
• m = 3 – number of phases,
• 2p = 8 – number of poles,
• n = 3000 rpm – rated speed,
• I_f = 5 A – nominal phase current,
• Ω_n = 0,8 – nominal efficiency,
• cosφ_n = 0,8 – rated power factor,
• B_r = 0,4 T – remanence ferrite,
• H_c = 270000 A/m – coercivity ferrite.

4.1 Synchronous motor with distributed winding on the stator in no-load condition

In the program FEMM is a no-load condition characterized by a zero current that passes through stator slots which means that of the cooper windings in the stator slots is replaced by air. In the rotor are located ferrite permanent magnets which are oriented in angle 90°. The magnetic field map and the normal component of magnetic flux density in no-load condition are shown in Fig. 2 and Fig. 3.

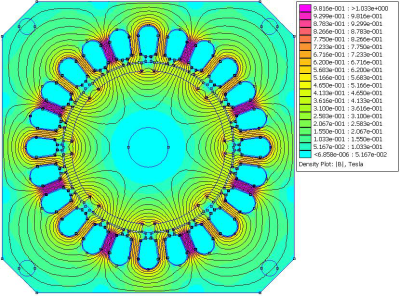
Fig. 2 The magnetic field map in no-load condition

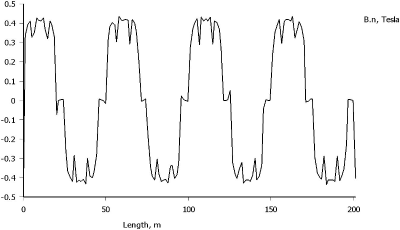
Fig. 3 The normal component of magnetic flux density in no-load condition

4.2 Synchronous motor with distributed winding on the stator in loaded condition

The investigated of synchronous motor has twenty four stator slots in which is distributed winding. Eight slots stator are loaded with a nominal phase current I_f = +5 A, eight slots stator are loaded with a nominal phase current I_f = -5 A and eight slots stator are loaded with a nominal phase current I_f = 0 A (the third phase is not powered). Ferrite permanent magnets are oriented at angle 90°. The magnetic field map and the normal component of magnetic flux density in loaded condition are shown in Fig. 4 a Fig. 5.

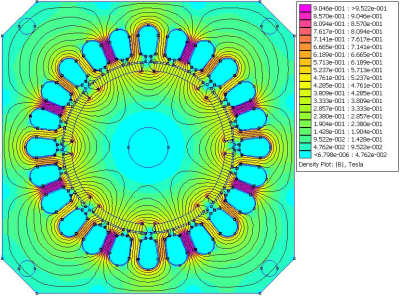
Fig. 4 The magnetic field map in loaded condition

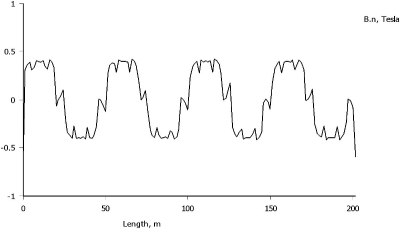
Fig. 5 The normal component of magnetic flux density in loaded condition

4.3 The condition armature reaction synchronous motor with distributed winding on the stator

The only difference in the condition armature reaction compared with loaded condition in program FEMM is that ferrite permanent magnets are replaced by air. The magnetic field map and the normal component of magnetic flux density in the condition armature reaction are shown in Fig. 6, Fig. 7, Fig. 8 and Fig. 9.

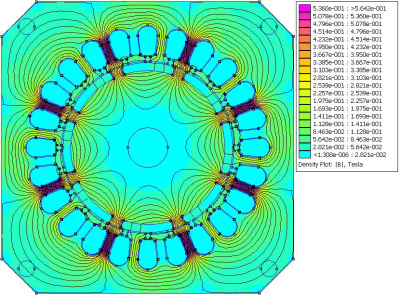
Fig. 6 The magnetic field map in the condition armature reaction in axis d

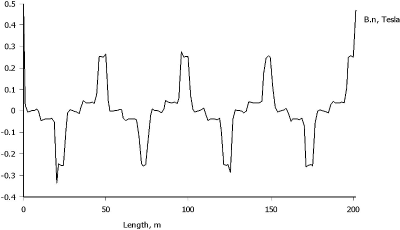
Fig. 7 The normal component of magnetic flux density in the condition armature reaction in axis d

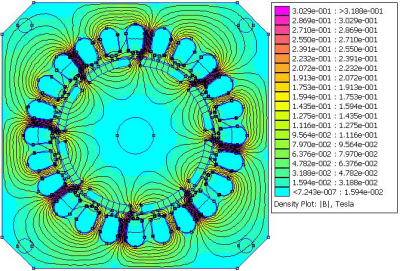
Fig. 8 The magnetic field map in the condition armature reaction in axis q

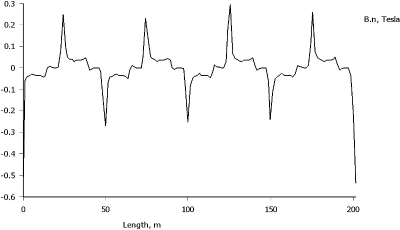
Fig. 9 The normal component of magnetic flux density in the condition armature reaction in axis q

Conclusion

This paper deals with of synchronous motor with distributed winding on the stator which has on the rotor ferrite permanent magnets. In the program FEMM is solution the magnetic fields of synchronous motor with distributed winding on the stator in no-load condition, in loaded condition and in the condition armature reaction. From the magnetic field map and the normal component of magnetic flux density is seen that distribution of magnetic fields lines is dependent on the size of the nominal phase current that passes through distributed winding and type used of permanent magnets.

References

1. KENJO, T.: Electric Motors and their Control. Oxford University Press, 1991.
2. HRABOVCOVÁ, V. et al.: Moderné elektrické stroje. 1st ed. vyd. Žilina: EDIS – vydavateľstvo ŽU, 2001. ISBN 80-7100-809-5, p. 217-223.
3. [3] MURÍN, J. 2009a: Metóda konečných prvkov. Proceedings lectures from the object Applied Mechanics. Lecture no. 2 – MKP, 2009. p. 1-10. Available at internet address:
   http://kmech.elf.stuba.sk/dokumenty/APLIMECH/prednaska_c2.pdf
4. MEEKER, D.: Finite Element Method Magnetics. User´s manual. Version 3.1, 2002, p. 6-12.

---

doc. Ing. Ľudovít Hüttner, PhD., Slovak University of Technology, Faculty of Electrical Engineering and Information Technology, Institute of Power and Applied Electrical Engineering, Ilkovičova 3, 812 19 Bratislava, Slovak Republic