Článok je zameraný na komplexný rozbor a porovnanie dvoch optimalizačných funkcií, ktoré sú definované ako vstavané funkcie v programovom prostredí MATLAB. Jedná sa o funkcie lsqnonlin a fmincon, ktoré sú určené pre použitie na nelineárnych funkciách s určitými obmedzeniami. Následne sú článku ďalej podrobne popísané jednotlivé princípy a metódy, ktoré tieto funkcie využívajú. Ich rozdiely budú demonštrované na príklade ladenia PID regulátora – optimálne nastavenie jednotlivých parametrov, pre sústavu popísanú v programe MATLAB vo voľne dostupnej schéme optsim.mdl.

Úvod

Optimalizácia je proces výberu najlepšej možnosti vzhľadom na dané kritériá z možných alternatív. Optimalizácia ako matematická disciplína poskytuje metódy riešenia (algoritmy) pre viaceré druhy účelových funkcií s rôznymi vymedzeniami prípustnej množiny riešení. Podrobnejšie bude opísaná možnosť optimalizácie nelineárnej účelovej funkcie v softvérovom prostredí MATLAB. Z daného prostredia bude demonštrované riešenie optimalizácie nelineárnej funkcie s obmedzeniami funkciami lsqnonlin a fmincon. Možnosti a výsledky použitia daných funkcií budú realizované prostredníctvom voľby parametrov PID regulátora pre rôzne kritériá kvality regulácie na podtlmenom systéme tretieho rádu v schéme optsim.mdl.

1. Optimalizačné metódy

1.1 Funkcia lsqnonlin

Funkcia lsqnonlin je vytvorená na optimalizáciu nelineárnych funkcií s obmedzeniami. Na riešenie optimalizačných problémov využíva metódu najmenších štvorcov. Funkcia realizuje rovnicu

(1)

kde vektor x obsahuje optimalizované parametre, f(x) je vektor výstupných hodnôt funkcie F(x). Funkcia pozná obmedzenia vo forme minima (lb) a maxima (ub) vstupu.

(2)

Funkcia lsqnonlin ponúka dva algoritmy pre optimalizáciu zadanej funkcie. Optimalizačné problémy veľkého rozsahu umožňuje riešiť pomocou algoritmu trust-region-reflective. Použitie daného algoritmu nie je možné pri poddeterminovanom systéme nelineárnych rovníc (počet elementov výstupného vektora f(x) musí byť rovný alebo väčší ako počet elementov vektora x). Optimalizačné problémy stredného rozsahu umožňuje riešiť pomocou algoritmu levenberg-marquardt. Daný algoritmus neumožňuje použitie maximálneho a minimálneho obmedzenia elementov vektora x [1].

1.2 Funkcia fmincon

Funkcia fmincon je vytvorená na hľadanie minima zadaného optimalizačného problému spojitých funkcií. Výstupom optimalizovanej funkcie môže byť iba skalárna hodnota.

(3)

Táto funkcia umožňuje použiť na nájdenie minima štyri rôzne algoritmy. Interior-point algoritmus je vhodný na riešenie optimalizačných problémov ľubovoľného rozsahu. Medzi jeho vlastnosti patria nízka spotreba pamäti,rýchle riešenie optimalizačných problémov veľkého rozsahu a nižšia presnosť v porovnaní s ostatnými algoritmami, ktorá je kompenzovateľná nastavením nižších tolerancií. Trust-region-reflective umožňuje riešenie optimalizačných problémov ľubovoľného rozsahu. Daný algoritmus vyžaduje od používateľa zadanie gradientov účelovej funkcie a zadanie jedného z typov obmedzení (minima a maxima alebo lineárne závislého obmedzenia).

Sqp algoritmus je vhodný na optimalizačné problémy malého alebo stredného rozsahu. Algoritmus dodržuje obmedzenia počas všetkých iterácií. Active-set algoritmus je vhodný na optimalizačné úlohy malého aj veľkého rozsahu. Výhodou algoritmu je, že dokáže uskutočňovať veľké skoky medzi iteráciami, čo urýchľuje riešenie danej úlohy [2].

2. Model systému optsim.mdl

Model predstavuje prístroj s pohonom reprezentuje podtlmený systém tretieho rádu s obmedzeniami predstavujúcimi obmedzenia pohonu. Pohon akceptuje vstupné hodnoty v rozmedzí <-2:2> a maximálnu zmenu vstupnej hodnoty 0,8 ij/s. V schéme sú tieto obmedzenia realizované prostredníctvom sériového zapojenia blokov Saturation (Limit) a Rate Limiter (Rate) na obrázku 1.

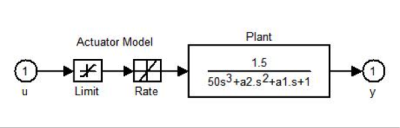
Obr.1 Subsystém obsahujúci model prístroja (Plant) s pohonom (Actuator Model)[1]

Regulácia modelu je realizovaná prostredníctvom PID regulátora. Parametre PID (Kp, Ki a Kd) regulátoru sú v danom prípade predmetom optimalizácie.

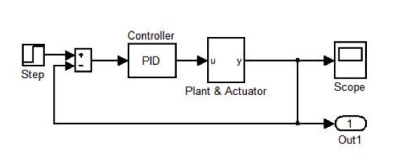
Obr.2 Model systému s PID regulátorom[1]

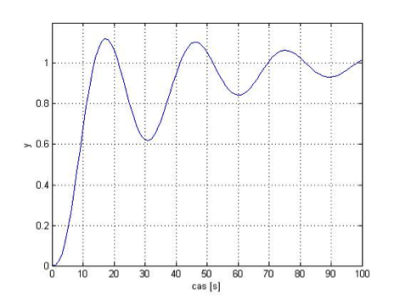
Obr.3 Regulátor s počiatočnými hodnotami [Kp, Ki, Kd]

3. Optimalizácia

Pri voľbe PID zložiek regulátora je potrebné voliť zložky s ohľadom na regulovaný systém, respektíve na požadovanú odozvu systému. Užívateľ má veľa kritérií, na základe ktorých môže posudzovať odozvu systému. Medzi kritéria môžu patriť integračné kritériá kvality, rýchlosť ustálenia regulácie, preregulovanie, rýchlosť regulácie a ďalšie [3],[4]. Pri použití funkcie lsqnonlin na výpočet parametrov regulátora môže užívateľ využiť viacero vyššie spomenutých kritérií a ich kombinácií, čo mu poskytuje výber z množstva možností nastavenia regulátora.

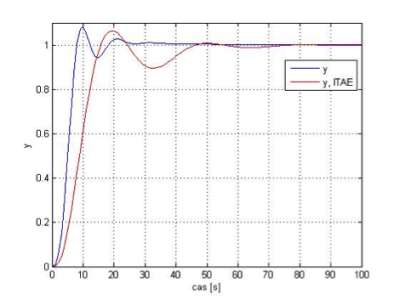
Obr.4 Regulátor s parametrami vypočítanými funkciou lsqnonlin s algoritmom TRR pre kritérium y a pre kritériá y a ITAE

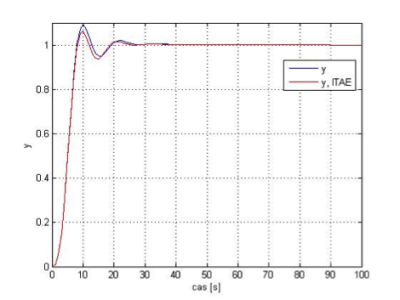
Obr.5 Regulátor s parametrami vypočítanými funkciou lsqnonlin s algoritmom LM pre kritérium y a pre kritériá y a ITAE

Obr.6 Regulačná odchýlka pre regulátor s parametrami vypočítanými funkciou lsqnonlin s algoritmami TRR a LM pre kritérium y

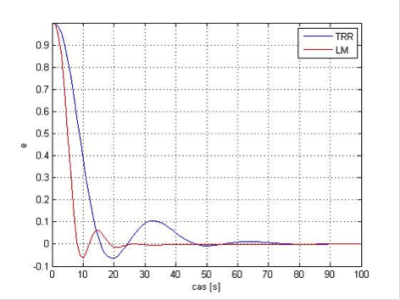
Obr.7 Regulačná odchýlka pre regulátor s parametrami vypočítanými funkciou lsqnonlin s algoritmami TRR a LM pre kritériá y a ITAE

Pri použití funkcie fmincon je potrebné zmeniť výstup simulácie tak, aby bola funkčná hodnota skalárna. Z tohto hľadiska je praktické pri tejto funkcii využívať integračné kritéria kvality ako kritéria pre optimalizáciu.

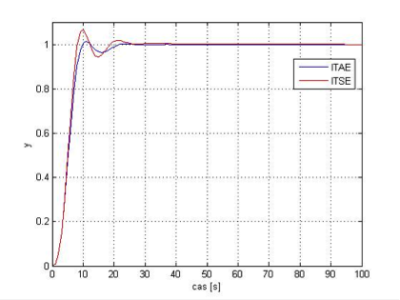
Obr.8 Regulátor s parametrami vypočítanými funkciou fmincon s algoritmom AS pre kritériá ITAE a ITSE

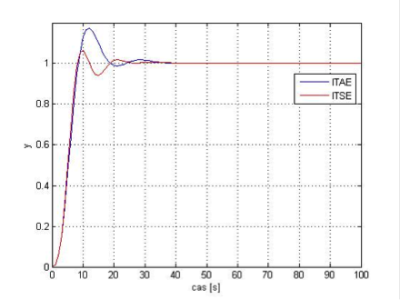
Obr.9 Regulátor s parametrami vypočítanými funkciou fmincon s algoritmom IP pre kritériá ITAE a ITSE

Obr.10 Regulátor s parametrami vypočítanými funkciou fmincon s algoritmom SQP pre kritériá ITAE a ITSE

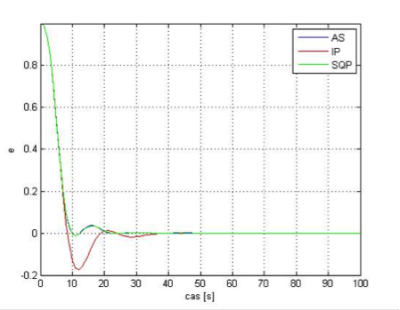
Obr.11 Regulačná odchýlka pre regulátor s parametrami vypočítanými funkciou fmincon s algoritmami AS, IP a SQP pre kritérium ITAE

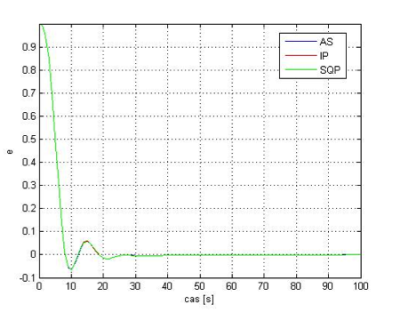
Obr.12 Regulačná odchýlka pre regulátor s parametrami vypočítanými funkciou fmincon s algoritmami AS, IP a SQP pre kritérium ITSE

V rámci optimalizácie je možné vidieť, že pri použití funkcie lsqnonlin dosahoval lepšie výsledky algoritmus LM pre vybrané kritériá optimalizácie. Napriek tomu je potrebné upozorniť na to, že optimalizáciou na základe štyroch integračných kritérií kvality je možné zostaviť až 24 možných kombinácii resp. 24 regulátorov pre daný model. Z daného experimentu nie je možné jednoznačne vyvodiť, ktorý z algoritmov poskytne lepšie parametre pre regulátor pri jednotlivých kombináciách kritérií.

Pri použití funkcie fmincon je možné je potrebné poukázať na takmer zhodujúce sa priebehy regulácie pre algoritmy AS a SQP. Pre danú funkciu neboli zobrazené priebehy regulácie pre algoritmus TRR s dôvodov problémového určenia gradientov optimalizovanej funkcie a takmer zhodnému priebehu regulácie s priebehom regulácie na základe počiatočných parametrov regulátora. V rámci porovnania jednotlivých optimalizačných funkcií je zaujímavé spomenúť počet iterácií, ktorý bol pre funkciu lsqnonlin v rozsahu 10-15 a pre funkciu fmincon 18-37. Ďalším zaujímavým parametrom resp. faktorom pri zohľadňovaní použitia jednotlivých funkcií a algoritmov je čas potrebný pre dosiahnutie optimalizovaných hodnôt. Týmto sa dostávame k obvyklej otázke rýchlosť realizácie vs. presnosť (rýchlosť ustálenia a nábehu, regulačná odchýlka, preregulovanie a ďalšie).

Tab. 1 Rýchlosti optimalizácie parametrov PID regulátora pre jednotlivé funkcie a algoritmy

optimalizované parametre	funkcia	algoritmus	čas skriptu / funkcie [s]
y	lsqnonlin	TRR	5,191 / 5,151
		LM	3,367 / 3,323
ITAE	fmincon	IP	9,48 / 9,439
		TRR	4,058 / 4,022
		SQP	18,043 / 18,01
		AS	20,225 / 20,186
ITSE	fmincon	IP	11,853 / 11,817
		TRR	3,998 / 3,963
		SQP	16,131 / 16,097
		AS	12,598 / 12,561

Záver

Optimalizačné funkcie lsqnonlin a fmincon poskytujú užívateľovi rozmanité možnosti optimalizácie účelových funkcií a to nielen na základe kritérií optimalizácie ale aj na základe voľby algoritmu a jednotlivých tolerancií. Uvedené funkcie je možné napriek rozdielom využiť na optimalizáciu tých istých účelových funkcií po úprave obmedzení a forme výstupných hodnôt danej účelovej funkcie.

Literatúra

1. www.mathworks.com
2. Róbert Bartko, MATLAB II. Optimalizácia, Vydavatelství VŠCHT Praha, 2008, ISBN 978-80-7080-691-3
3. http://www.mathworks.com/videos/global-optimization-with-matlab-products-81716.html
4. http://www.mathworks.com/products/optimization/description2.html

---

Spoluautorom článku je Tatiana Mudráková