Stereoskopia je jedným zo spôsobov ako určiť polohu objektu v trojrozmernej vizuálnej scéne. V článku sa venujeme návrhu postupu určenia horizontálnej, vertikálnej a hĺbkovej priestorovej súradnice snímaného bodu s využitím goniometrie a technických vlastností kamier a kamerových systémov tak, aby tieto postupy boli aplikovateľné pre ľubovoľné situácie a parametre. Správnosť navrhnutých postupov je overená simuláciou v programe Matlab. Článok je výstupom študentského projektu realizovaného v rámci predmetu „Videokomunikácie“ a ukazuje jednoduché matematické riešenie úlohy určenia pozície sledovaného objektu navrhnuté študentom v spolupráci s pedagógom.

Úvod

Stereoskopia je jednou z metód záznamu trojrozmernej vizuálnej scény, ktorá umožňuje zaznamenať aj informáciu o hĺbke. Využíva veľmi podobný princíp ako ľudský zrakový systém. Objekt je zaznamenaný dvoma kamerami, ktoré majú rôznu polohu. Následne je na základe týchto stereoskopických snímok možné vytvoriť priestorový model resp. obraz reality, ktorý sa javí ako reálny 3D model reality. Pridanou hodnotou využitia stereoskopie, je možnosť, na základe stereoskopických snímok zistiť pozíciu objektu v reálnom priestore. Využitím týchto snímok a jednoduchej goniometrie je potom možné, určiť polohu objektu v trojrozmernej (3R) vizuálnej scéne (VS). Ide o istú alternatívu k estimácii (odhadu) priestorových súradníc prostredníctvom laseru, elektromagnetických vĺn vysielaných radarom na základe niekoľkých ortogonálnych pohľadov na 3R vizuálnu scénu [1].

1. Projekčné modely

Každý reálny snímaný bod X_(x;y;z) zo súradnicového systému 3R VS je premietnutý na projekčné plátno – priemetňu – ako bod x_(i;j). Podľa spôsobu premietania je možné techniky projekcie rozdeliť na dve [2]. Prvou je ortogonálna projekcia. Ide o spôsob projekcie, pri ktorom sú spojnice snímaného bodu a jeho obrazu na priemetňu П navzájom kolmé, teda stred premietania (bod O) je v nekonečne (obr. 1). Druhou je perspektívna projekcia. V tomto prípade sa snímaný bod sústredne premietne na priemetňu П cez stred premietania (obr. 2). Nech bod S na snímanom obraze, pre ktorý platí sa nazýva stredom snímaného obrazu, bod „s“ je obrazom bodu „S“ na priemetni П, potom vzdialenosť sa nazýva ohnisková vzdialenosť a priamka sa nazýva optickou osou. Zobrazenie spĺňajúce tieto podmienky sa nazýva kolmá perspektívna projekcia [3] (obr. 3).

Obrázok 1: Ortogonálna projekcia

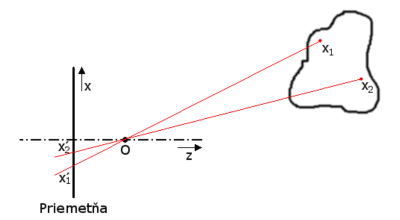
Obrázok 2: Perspektívna projekcia

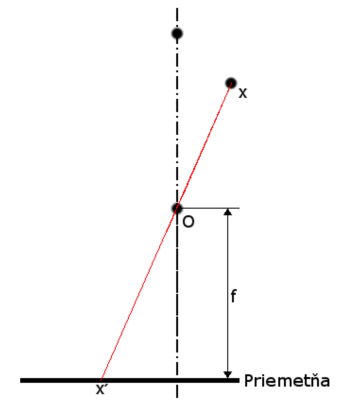
Obrázok 3: Perspektívna projekcia a model pinhole kamery

Reálne kamery a fotoaparáty je možné popísať pomocou perspektívnej projekcie. Najjednoduchším matematickým popisom, ktorý budeme uvažovať, fungujúcim na princípe perspektívnej projekcie je tzv. pinhole kamera [3]. Ide o idealizovaný model, v ktorom sa priemetňa nachádza za nepriesvitnou bariérou, v ktorej je nekonečne malý otvor „pinhole“, dierka (obr. 3). Obraz na takejto priemetni je voči trojrozmernej vizuálnej scéne zrkadlený cez horizontálnu aj vertikálnu os.

2. Základné optické vlastnosti kamery/fotoaparátu

Medzi základné optické vlastnosti každej kamery, resp. fotoaparátu patria ohnisková vzdialenosť, zorný uhol a rozmery priemetne [4, 5] (obr. 4). Ohnisková vzdialenosť, označovaná „f“ je vzdialenosť medzi šošovkou a priemetňou uvedená v mm, ide o rozmer, ktorý dokážeme meniť a tým vykonávať tzv. zoom/unzoom – približovanie/odďaľovanie snímky. Zorným uholom „α“ rozumieme uhol, ktorý je kamera schopná zachytiť, mení sa v dôsledku zmeny ohniskovej vzdialenosti. Veľkosť rastra fotografie v pixeloch je označovaná ako rozmery priemetne. Všetky tieto parametre sú pre každú kameru jedinečné a ich hraničné hodnoty sú dané výrobcom (uvedené na objektívoch apod.).

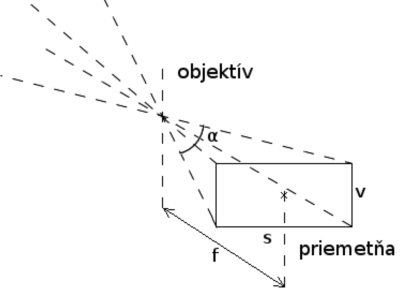
Obrázok 4: Základné parametre kamery

3. Kamerové systémy

Keďže stereoskopia funguje na veľmi podobnom princípe ako ľudský zrakový systém, je pre vytváranie stereoskopických obrazov nutnou podmienkou v jednom časovom okamihu, zaznamenať objekt aspoň dvoma kamerami, umiestnenými v rôznych pozíciách. Teoreticky je možné snímky zachytiť z ľubovoľných pozícií. Pre zjednodušenie realizácie zavedieme súradnicový systém s počiatkom v objektíve kamery K1. Kamera K2 bude umiestnená na osi x a sledovaný bod sa bude v 3R VS nachádzať na takej pozícii, že jeho priemet po perspektívnej projekcii sa zobrazí na priemetniach oboch kamier celý. Následne, podľa vzájomnej pozície optických osí použitých kamier môžeme uvažovať dva stereoskopické kamerové systémy.

Nesúosový kamerový systém, ktorého kamery sú umiestnené tak, že optické osi kamier sa v presne definovanom bode pretínajú, teda optické osi kamier nie sú kolmé na spojnicu kamier (obr. 5). Súosový kamerový systém, ktorého kamery sú umiestnené tak, že ich optické osi sa nepretínajú, ale sú rovnobežné a teda sú aj kolmé na spojnicu kamier (obr. 6). Pre jednoduchosť, v našom príspevku analyzujeme iba súosový kamerový systém.

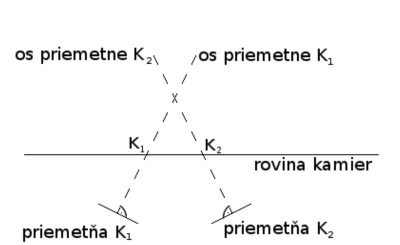
Obrázok 5: Nesúosový stereoskopický kamerový systém

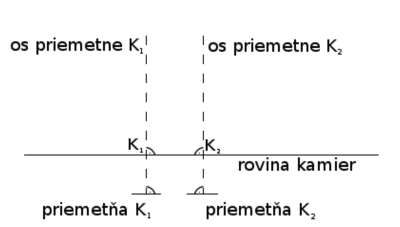
Obrázok 6: Súosový stereoskopický kamerový systém

4. Určenie polohových súradníc bodu

Nech má každý bod v priestore tri súradnice X_(h,v,d) – horizontálnu (h), vertikálnu (v), hĺbkovú (d). Po jeho perspektívnej projekcii má v rovine priemetne len dve súradnice x_(i,j) – horizontálnu (i) a vertikálnu (j). Uvažujme prípad, dvoch totožných kamier, popísaných pomocou perspektívnej projekcie. Pre zjednodušenie výpočtov uvažujme taký prípad, v ktorom sú obe kamery umiestnené vodorovne a predpokladáme súradnicový systém so stredom v K1 a horizontálnou osou totožnou so spojnicou kamier K1 a K2, t.j. súosový stereoskopický kamerový systém (obr. 6). Známymi veličinami sú (obr. 7) vzdialenosť kamier, označená „a“, ohnisková vzdialenosť kamery K1 resp. K2, označená „f“, šírka a výška priemetne kamery K1 resp. K2 v označené „S“ a „V“. Všetky vzdialenosti pri výpočtoch budeme uvažovať v pixeloch.

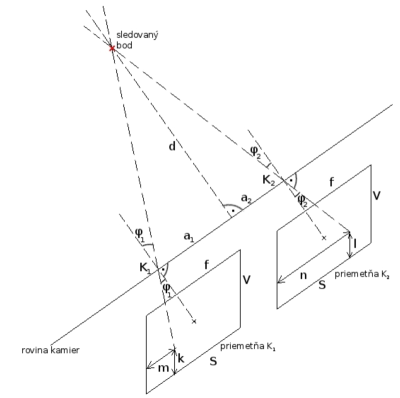
Obrázok 7: Uvažované rozmiestnenie kamier, priemetní, priemetov a sledovaného bodu

Začneme určením hĺbkovej súradnice bodu, teda vzdialenosti bodu od snímacích kamier a vychádzame pri tom z obr. 7. Hľadaný bod sa po perspektívnej projekcii premietne na priemetňu K1 (1) a priemetňu K2 (2) vo vzdialenosti

(1)

(2)

kde m je vzdialenosť od ľavého okraju priemetne K1 a n od ľavého okraju K2. Pre uhol φ1 (v prípade K1) a φ2 (v prípade K2) platí

(3)

(4)

Potom pre K1 (5) a K2 (6) platí

(5)

(6)

(7)

Z toho, pre hĺbkovú súradnicu objektu bude platiť vzťah

(8)

Dosadením (1) a (2) do (8) získavame výsledný vzťah pre výpočet hĺbkovej súradnice snímaného bodu

(9)

kde menovateľ predstavuje horizontálne posunutie snímaného bodu na priemetni kamery K2 voči jeho horizontálnej polohe na priemetni kamery K1. Toto posunutie budeme nazývať disparita. Na základe vyššie uvedených vzťahov je možné odvodiť vzťah pre horizontálnu súradnicu sledovaného bodu

(10)

S využitím (1) a (9) dostávame výsledný vzťah pre horizontálnu súradnicu snímaného bodu

(11)

Vertikálnu súradnicu sledovaného bodu je možné určiť nasledovne. Hľadaný bod sa po perspektívnej projekcii premietne na priemetňu K1 (12) a priemetňu K2 (13) vo vzdialenosti

(12)

(13)

kde k a l je vzdialenosť v od dolného okraju priemetne. Vzhľadom na to, že uvažujeme súradnicový systém s počiatkom v bode, ktorý predstavuje objektív kamery K1a objektív kamery K2 leží na osi x sa tieto dve súradnice navzájom rovnajú a teda platí

(14)

Vzhľadom na to budeme ďalej pokračovať už len s použitím goniometrie pre kameru K1. Ďalej je nutné určiť priblíženie kamery, teda koľkokrát je objekt na priemetni zmenšený. Z obr. 7 je zrejmé

(15)

kde x_i1 je odvodené na základe (1). A teda z tohto vzťahu jednoducho odvodíme vertikálnu zložku

(16)

S využitím (1), (11) a (14) dostávame výsledný vzťah pre vertikálnu súradnicu snímaného bodu

(17)

Na záver uvedieme, že všetky odvodené vzťahy je možné jednoducho previesť aj do metrickej mierky a to

(18)

kde y’ je rozmer v pixeloch a DPI (Dots per Inch) je merná jednotka v počítačovej grafike (množstvo bodov, t.j. množstvo pixelov v rade dlhom jeden palec). V nasledujúcej podkapitole dokážeme správnosť odvodených vzťahov pomocou simulácie v programovom balíku Matlab.

5. Počítačová simulácia

V simulačnom programe Matlab sme navrhli program, ktorý na základe nami odvodených vzťahov vypočíta polohu sledovaného bodu. Budeme uvažovať dve totožné kamery s totožnými parametrami a vlastnosťami. Program začína inicializáciou známych vstupných premenných, t.j. rozmerov priemetní, vzdialeností kamier a ohniskovej vzdialenosti. Ďalej sa náhodne vygenerujú súradnice 10 náhodných bodov v priestore, ktoré budeme v jednotlivých krokoch programu sledovať.

V nasledujúcej časti programu je bod pomocou perspektívnej projekcie premietnutý na dve priemetne. Ide o iteračnú metódu s krokom 1px. Hľadá sa priesečník priamky, ktorá spája bod a objektív kamery s priemetňou. Priesečníkom sa stáva bod, ktorý splní podmienku presnosti 1px, t.j. jeho súradnice sa od jemu prislúchajúcemu bodu na priemetni líšia o menej ako 1px. Pozícia tohto bodu je následne zaznamenaná vzhľadom na pozíciu na priemetni, teda ide o celé číslo označujúce polohu pixelu, do ktorého sa sledovaný bod premietol. V rámci hľadania obrazu bodu na priemetni sa overuje aj podmienka, či má vôbec daný bod takú polohu, že sa premietne na obe priemetne kamier. Pokiaľ nie, tak sa vygenerujú súradnice pre nový bod a celý proces hľadania priesečníka sa opakuje.

Po zistení a zaznamenaní polohy obrazov bodu na priemetniach nasleduje už samotné určovanie pôvodnej polohy sledovaného bodu, pomocou vzorcov odvodených v teoretickej časti tohto článku. Do troch matíc HOR, VER, DEP sa zaznamenajú údaje o horizontálnej, vertikálnej a hĺbkovej súradnici sledovaného bodu, ktoré boli vygenerované, určené podľa nami odvodených vzťahov. Chyba výpočtu je určená ako

(19)

kde X označuje hodnotu niektorej zo súradníc vygenerovanú programom, Xodv predstavuje jej hodnotu určenú pomocou vyššie odvodených vzťahov a predstavuje hodnotu chyby v dB. Nakoniec sa priemetne, objektívy, obrazy a sledovaný bod vykreslia do trojrozmerného grafu, aby mohol užívateľ programu ľahšie sledovať jeho zmeny polohy a celý postup sa opakuje pre ďalší náhodne vygenerovaný bod.

6. Analýza výsledkov počítačovej simulácie

Ako bolo uvedené vyššie, po vykonaní simulácie dostaneme výsledky v tabuľkovej aj grafickej podobe. Na obr. 8 možno vidieť grafický výstup zo simulácie, na ktorom je zobrazený sledovaný bod (čiernou), priemetne, obrazy sledovaného bodu a objektívy (modrou sú označené parametre ľavej a červenou pravej kamery). Graf slúži najmä pre užívateľa na lepšie zorientovanie toho, kde sa nachádza sledovaný bod a jeho obrazy na priemetniach.

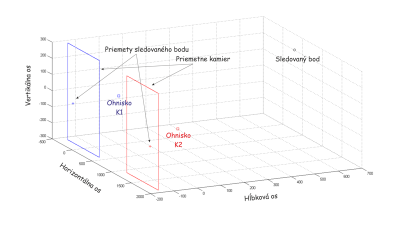
Obrázok 8: Výstup počítačovej simulácie

Obr. 9 až 11 a tab. 1 ponúkajú ukážku výstupu určenia chyby priamo z prostredia Matlab. Ide o kombináciu textového výstupu hodnôt z matíc HOR, VER a DEP a grafického prevedenia závislosti nepresnosti jednotlivých súradníc od polohy sledovaného bodu, čo nám umožňuje urobiť si predstavu o presnosti určenia polohy sledovaného bodu. Tab. 1 uvádza výstup z matíc HOR, VER a DEP. Na porovnanie sa do týchto matíc zapisujú údaje o sledovanom bode – generovaná hodnota súradnice, vypočítaná hodnota súradnice a chyba výpočtu. Ako je možné vidieť z tab. 1, chyby výpočtu sa pohybujú na pomerne malých úrovniach (v absolútnych hodnotách menej ako 3px), čo dokazuje správnosť navrhovaného postupu.

V rámci jednotlivých súradníc sa generujú body so širokým spektrom súradníc a vidíme, že prakticky pri všetkých z nich sú hodnoty chyby pomerne nízke a približne rovnako vysoké. Nie je možné vyniesť všeobecný záver, konštatujúci, v ktorej oblasti 3R VS sú súradnice sledovaných bodov určované s najväčšou presnosťou. Chyba výpočtu je určená najmä presnosťou priemetov týchto bodov na jednotlivé priemetne, ktorú môžeme zvýšiť zväčšením hustoty rastra fotografie, t.j. zväčšením parametra DPI. Čím budú hodnoty DPI vyššie, tým bude aj priemet bodu na priemetni, teda pixel, do ktorého sa bod premietne, viac zodpovedať jeho geometrickému obrazu.

Horizontálna			Vertikálna			Hĺbková
Generov. [px]	Určená [px]	Chyba [dB]	Generov. [px]	Určená [px]	Chyba [dB]	Generov. [px]	Určená [px]	Chyba [dB]
1222	1222,2	37,9	650	650,1	38,1	638	641	23,3
1370	1369,4	33,6	212	211,9	33,3	629	632	23,2
418	419,3	25,1	75	75,2	25,7	888	885,8	26,1
1059	1057,8	29,5	750	749,1	29,2	683	683,9	28,8
1042	1039,4	26,0	293	292,3	26,2	886	885,8	36,5
1149	1148,1	31,1	473	472,6	30,7	656	659,8	22,4
735	731,4	23,1	87	86,6	23,4	794	795,1	28,6
53	52,5	20,3	559	554	20,5	881	875,5	22,0
1018	1016,5	28,3	413	412,4	28,4	823	824,2	28,4
588	585,3	23,4	249	247,8	23,2	651	650,3	29,7

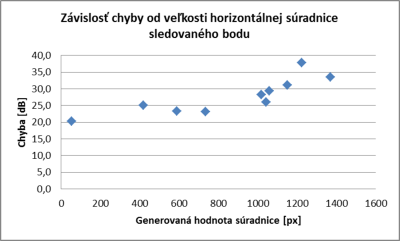
Obrázok 9: Závislosti chyby od veľkosti horizontálnej súradnice sledovaného bodu

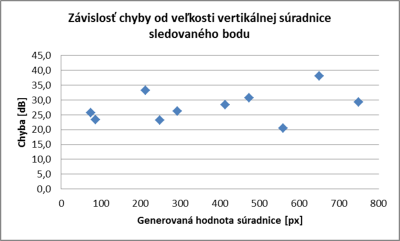
Obrázok 10: Závislosti chyby od veľkosti vertikálnej súradnice sledovaného bodu

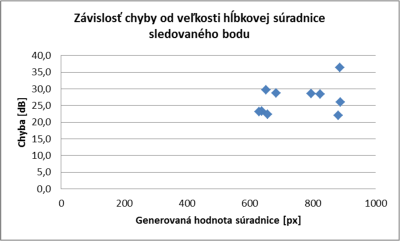
Obrázok 11: Závislosti chyby od veľkosti hĺbkovej súradnice sledovaného bodu

7. Záver

Pomocou znalostí z trigonometrie sme odvodili vzťahy pre známu metódu stereoskopického záznamu trojrozmernej vizuálnej scény, ktorým je možné určiť polohu sledovaných bodov, resp. objektov. Metódu sme overili aj v programe v simulačnom prostredí Matlab, ktorý potvrdil jej efektívnosť a presnosť. Chyba určenia polohy sledovaného bodu závisela od presnosti celého systému na 1px, čím mohlo dôjsť k istému skresleniu. V prezentovanom príklade využitia tejto metódy sa hodnota súradníc určených pomocou metódy líšila od reálnych súradníc v rozmedzí 20,5 až 37,4dB. Ide o pomerne nízke hodnoty chýb. Keďže sa pozície sledovaných bodov generujú náhodne, je takýmto spôsobom možné overiť presnosť určovania súradníc bodov vyskytujúcich sa na pomerne veľkej časti sledovanej 3R VS.

Zaujímavosťou je, že presnosť určovania horizontálnych súradníc je v každom z prípadov približne rovnaká ako presnosť určenia vertikálnych súradníc, zodpovedajúcich týmto horizontálnym súradniciam. Je to spôsobené tým, že perspektívna projekcia, ktorú využívame, je premietaním trojrozmernej vizuálnej scény do dvojrozmernej – na priemetňu, ktorej okraje sú umiestnené práve v týchto dvoch smeroch (horizontálnom a vertikálnom). Preto sú tieto dve nepresnosti v našom modely prepojené, čo vyplýva aj z rovnice (16). Ďalším možným pokračovaním projektu by mohlo byť overenie navrhovanej metódy v reálnych podmienkach s reálnymi fotografiami a ich porovnanie s výsledkami zo simulácie, ktorá jasne ukazuje výhody tejto metódy.

Zdrojové súbory simulácie je možné stiahnuť z adresy: http://web.tuke.sk/fei-ldipv/OK/stereoskopia.zip

Literatúra

1. KOVÁČ, O.; MIHÁLIK, J.: Estimácia priestorových súradníc modelu ľudskej hlavy na báze dvoch ortogonálnych pohľadov. In: Electrical Engineering and Informatics 4, Proc. of the Faculty of Electrical Engineering and Informatics of the Technical University of Košice. FEI TU, 2013, p. 401- 405.
2. WANG, G.; WU, J.: Guide to Three Dimensional Structure and Motion Factorization, Springer, 2011.
3. DURAS, T.: Stereoskopia v Počítačovej grafike, bakalárska práca, UK FMFI, Bratislava, 2010.
4. NIKON: Learn & Explore – Understanding Focal Lenght, [online], [cit: 1.4.2014], dostupné na internete:
   http://www.nikonusa.com/en/Learn-And-Explore/Article/g3cu6o2o/understanding-focal-length.html
5. NIKON: Digital SLR Camera Basics, [online], [cit: 1.4.2014], dostupné na internete
   http://imaging.nikon.com/history/basics/19/01.htm
6. The Turing Institute: History of Stereo Photography, 1996, [online], [cit: 1.4.2014], dostupné na internete:
   http://www.arts.rpi.edu/~ruiz/stereo_history/text/historystereog.html

---

Spoluautorom článku je Ing. Ondrej Kováč, Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach