Tento príspevok je zameraný na rozpoznávanie hlasových príkazov pomocou spektrogramov. Metóda porovnávania spektrogramov bola zvolená s ohľadom na nízky výpočtový výkon vstavaného systému FOX Board. Porovnanie spektrogramov sa robilo pomocou Euklidovej vzdialenosti a navrhol sa systém zníženia výpočtového zaťaženia pomocou redukcie matíc a metóda bola vylepšená pomocou porovnávania spektrogramov s použitím 3 okienok: Blackman-Harris okienko, Hammingove okienko a pravouhlé okienko.

Úvod

Najprirodzenejším komunikačným prostriedkom pre človeka je hovorená reč. Vzhľadom na to sa už veľa rokov skúma rozpoznávanie reči počítačmi. Tento výskum je už na celkom vysokom stupni pokroku, ale stále zostávajú mnohé problémy súvisiace s tým, že hlas človeka je stále iný a prostredie vnáša do signálu hovoreného slova šum. Výskum je zameraný hlavne na anglický jazyk a rozpoznávanie prebieha na výkonných systémoch. Na katedre KTPE sme sa zamerali na rozpoznávanie slovenského jazyka a hlavne na systémy s nízkym výpočtovým výkonom ako sú vstavané systémy. Vzhľadom na veľký výber vstavaných (embedded) systémov bol pre riadenie a rozpoznávanie izolovaných slov zvolený ucelený vývojový vstavaný systém FOX Board, ktorý sa používa na katedre KTPE už dlhšie.

Vývojový systém FOX Board

Vývojový systém FOX Board pozostáva z plošného spoja s rozmermi 66 x 72 mm, na ktorom sa nachádzajú vstupno-výstupné rozhrania, mikroprocesor ETRAX 100LX, napájanie a LED diódy. Mikroprocesor ETRAX 100LX s architektúrou RISC CPU s 32 – bitovým dátovým a adresným formátom je taktovaný na frekvenciu 100 MHz. Mikroprocesor má k dispozícii 8 kB veľkú vyrovnávaciu cache pamäť. Vývojový systém FOX Board je znázornený na nasledujúcom Obr.1 [1].

Obr.1 FOX Board

Operačný systém je uložený v 8 MB veľkej FLASH pamäti. Pamäť RAM má veľkosť 32 MB. Veľkou výhodou tohto vstavaného systému je, že dátový priestor sa dá zvýšiť využitím vstupno-výstupného rozhrania USB (Universal Serial Bus), ktoré sú na plošnom spoji v počte 2.

Spektrogramy

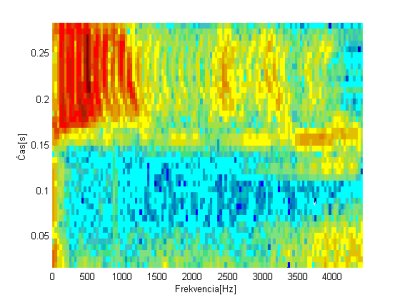
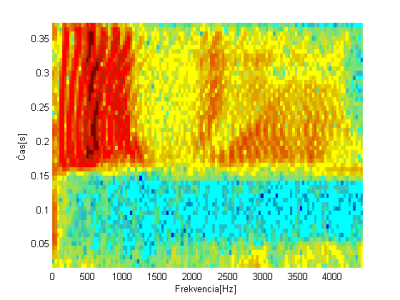
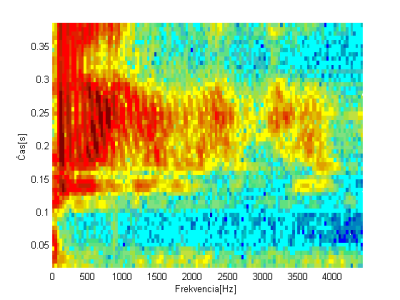
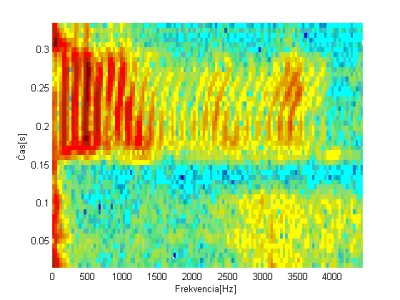
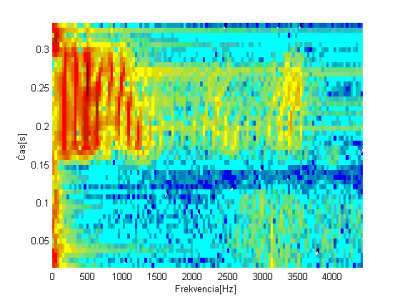
Pre systém rozpoznávania izolovaných slov pomocou vstavaného systému sa hľadalo čo najjednoduchšie riešenie vzhľadom na nízky výpočtový výkon zvoleného vstavaného systému. Pri rozpoznávaní slov sa má porovnaním nejakého testovaného slova nájsť podobnosť s referenčným slovom. Hovorí sa o podobnosti, keďže, ako sa spomínalo skôr, 2 zvukové záznamy toho istého slova vysloveného aj tým istým rečníkom nie sú nikdy zhodné. Pri hľadaní podobnosti sa vyskúšala aj podobnosť spektrogramov, ktoré prezentujú grafickú podobu zvuku. Podobnosť spektrogramov môžeme vidieť na Obr. 2-a) a 2-b). Spektrogram ukazuje ako sa mení priebeh spektra s časom – modrá farba predstavuje nízku energiu a červená najvyššiu [2]. Najvyššiu energiu majú frekvencie do 1500 Hz pri čase od 0,15s po koniec slova (Obr.2-a) a 2-b)). Môžeme si všimnúť, že dĺžka vysloveného slova „stop“ je u obidvoch rečníkov odlišná. V prvom prípade 0,3s (Obr.2-a) ) a v druhom dokonca 0,37s (Obr.2-b) ).

(a)

(b)

(c)

Obr. 2 Spektrogramy a) slova “stop” vysloveného rečníkom 1, b) slova “stop” vysloveného rečníkom 3 a c) slova “vpravo” vysloveného rečníkom 1

Ak si k porovnaniu pridáme ďalšie slovo „vpravo“ vysloveného rečníkom 1 (Obr. 2-c) ) a porovnáme ho so spektrogramami slova „stop“ vidíme, že sa navzájom odlišujú. Hustota je pri slove „stop“ najvyššia hlavne na konci slova a pri slove „vpravo“ pri frekvenciách od 1100 Hz hlavne v strede slova. Podobnosť spektier v čase pri rovnakých slovách aj pre rôznych rečníkov (Obr.2-a) a 2-c)) a naopak rozdiely pri rôznych slovách (Obr.2-a) a 2-c) ) umožňujú postaviť náš klasifikátor reči izolovaných slov na porovnaní spektrogramov.

Vzorkovacia frekvencia nahrávania bola zvolená na 8820 Hz a pre dĺžku DFT (diskrétna fourierová transformácia) , bola zvolená 256 kvôli zníženiu počtu dát vzhľadom na použitú vzorkovaciu frekvenciu. Počet prekrývajúcich rámcov musí byť menší ako dĺžka okienka a preto bol zvolený tento počet na 200 [3]. Pre výpočet spektrogramov boli použité vzťahy [4]:

(1)

kde

(2)

(3)

kde h(n) je použité dané okienko[5]:

• pre Hammingove okienko

• pre pravouhlé okienko

• pre Blackman-Harris okienko

Spektrogram je v matematickom vyjadrení vlastne matica, v ktorej riadky predstavujú čas a stĺpce frekvenciu. Táto matica má však veľké rozmery, preto bola prvá fáza práce zameraná na návrh redukcie jej rozmerov za účelom zrýchlenia výpočtov a dosiahnutie menšieho dátoveho zaťaženia. Pre redukciu bola zvolená metóda, pri ktorej sa rozdelila daná matica spektrogramu na menšie časti a každá submatica bola náhradená jednou číselnou hodnotou, ktorá ju charakterizovala, čím došlo k redukcii veľkosti matice. Jednou z možností pre výpočet submatice je použitie aritmetického priemeru alebo jeho modifikácií. Vzhľadom na to, že matica má viac stĺpcov ako riadkov bol zvolený pre rozdelenie obdĺžnikový tvar submatice alebo inak povedané, pre ďalšie experimenty bola zvolená obdĺžniková plocha spektrogramu. Ak by sa zvolili čím väčšie submatice, tak by sa dostala tým menšia výsledná matica (spektrogram), ale na druhej strane by sa znížila presnosť rozpoznávania slov.

Pri veľmi rozdielnych slovách by táto redukcia mohla fungovať dobre, ale pri riadení mechatronického systému sa musia voliť podobné slová ako „vľavo“ a „vpravo“. Pri veľmi malej submatici by sa naopak dostatočné zníženie rozmerov výslednej matice nedosiahlo a trvanie výpočtov by bolo dlhšie a náročnejšie. Z tohto dôvodu sa zvolili rozmery submatice 5 x 3: pričom 5 stĺpcov zodpovedalo frekvencii a 3 riadky časovému posunu. Porovnanie dvoch redukovaných matíc bolo rozhodnuté realizovať pomocou výpočtu Euklidovej vzdialenosti. Pre túto vzdialenosť musel byť navrhnutý spôsob úpravy veľkosti matice oboch porovnávaných slov (jedno berieme ako referenčné a druhé ako testované) na rovnakú veľkosť. Počet stĺpcov je stále rovnaký, frekvencia je stále rovnaká, ale počet riadkov matice je odlišný v závislosti od rozdielnej dĺžky toho istého slova. Existujú dve možnosti úpravy počtu riadkov:

• znížiť počet riadkov väčšej matice (dlhšieho slova) na úroveň menšej matice (kratšieho slova) alebo
• zvýšiť počet riadkov menšej matice (kratšieho slova) na rovnaký počet ako má väčšia matica (dlhšie slovo).

Pri rozhodovaní bolo dôležité uvažovať hlavne o správnej identifikácii začiatku a konca slova. Pri redukovaní prvých riadkov matice (začiatok slova), a ak by bola za tento začiatok slova určená až niektorá z ďalších foném, tak odstrihneme i začiatok slova. Naopak, pri redukovaní posledných riadkov matice by pri nesprávnom určení konca slova došlo k orezaniu konca slova. Preto bola pre experimenty zvolená druhá možnosť a to zvýšenie počtu riadkov menšej matice. Pridávané riadky budú mať nulovú hustotu, a tým sa nepoškodí identifikovaný začiatok alebo koniec slova. Riadky je možné do matice pridávať 3 spôsobmi:

• pridaním riadkov pred identifikovaný začiatok slova,
• pridaním riadkov za identifikovaný koniec slova,
• kombináciou predchádzajúcich dvoch prípadov, t.j. pridanie riadkov pred identifikovaný začiatok slova a aj za identifikovaný koniec slova.

Tretí spôsob pridávania riadkov pred a súčasne aj za koniec slova skrýva v sebe problém. Ak je potrebné pridať nepárny počet riadkov, tak sa musí rozhodnúť koľko riadkov pridať pred začiatok slova a koľko za koniec slova. Pri párnom počte je situácia zdanlivo jednoduchšia, nakoľko nám umožňuje pridanie rovnakého počtu riadkov pred aj na koniec. Treba si ale uvedomiť, že na zlepšenie detekcie začiatku alebo konca slova by bolo vhodné uvažovať aj o asymetrickom rozdelení. Pri ďalšom experimentovaní bol vzhľadom pre čo najväčšie zjednodušenie systému rozpoznávania izolovaných slov vybraný postup, pri ktorom boli riadky s nulovou hustotou zaraďované na koniec slova. V ďalšom kroku bolo potrebné rozhodnúť, kedy zvýšenie riadkov matice spraviť. Boli dve možnosti:

• úprava ešte neredukovanej matice (celý spektrogram) alebo
• úprava redukovanej matice po aritmetickom priemere.

Prvá možnosť úpravy celého spektrogramu je náročnejšia na čas a výpočtovú silu. Je rozdiel pridávať maticu o rozmeroch 5 x 125 alebo 5 x 25, a preto bol vybraný postup úpravy redukovanej matice až po jej redukcii pomocou aritmetického priemeru. Na Obr.3-a) je spektrogram slova „stop“ redukovaného aritmetickým priemerom submatice s počtom riadkov 14. Na Obr.3-b) je spektrogram po pridaní riadkov – počet riadkov 19 bol zvolený pre konkrétny príprad porovnania slova „stop“ vysloveného rečníkom 1 so slovom „vpravo“ vysloveného rečníkom 1 s počtom riadkov 19 (obr.3-c) ). Priebeh spektra v čase (riadky) ostal síce na pozícii riadkov 8 – 14, ale na riadkoch 15 – 19 sú samé nuly (obr.3-c) ).

(a)

(b)

(c)

Obr.3 Spektrogramy: a) slova „stop“ s počtom riadkov 14 vysloveného rečníkom 1 po redukcii pomocou aritmetického priemeru, b) slova „stop“ vysloveného rečníkom 1 po pridaní riadkov na 19 a c) slova „vpravo“ vysloveného rečníkom 1 po redukcii aritmetickým priemerom s počtom riadkov 19

V ďalšom kroku práce bolo odskúšané porovnanie spektrogramov pomocou Euklidovej vzdialenosti. Pri rozdielnych slovách by podľa teoretických predpokladov mala byť Euklidova vzdialenosť veľká. Na obr.4 je vypočítaná Euklidova vzdialenosť 10,7857. Keďže porovnávame 2 slová systémom každý s každým, tak upravený spektrogram kratšieho slova (Obr.4-b) ) je v danom riadku príslušného slova (Obr.4-a) ). Upravovaná bola matica slova „stop“ (Obr.4-a) ), a preto upravený spektrogram je na Obr.4-b) ).

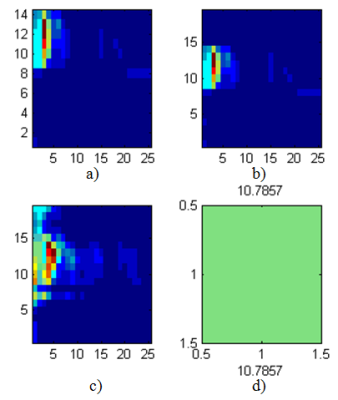
Obr.4 Porovnanie a) spektrogramu slova „stop“ vysloveného rečníkom 1, b) upraveného spektrogramu slova“stop“, c) spektrogramu slova „vpravo“ a d) s Euklidovou vzdialenosťou

Pri rovnakých alebo veľmi podobných slovách je Euklidova vzdialenosť malá, pričom pri rovnakých slovách má byť nižšia ako pri podobných, aby bolo možné správne rozpoznať testované slovo. Euklidova vzdialenosť slov „dole“-1 a „dole“-3 vyslovených tým istým rečníkom 3 – žena – je veľmi malá, len 0,884472. Pri podobných slovách ako sú slová „hore“-1 a „dole“ vyslovených tiež rečníkom 3 – žena – je táto vzdialenosť tiež nízka 1,3767. Z porovnávaní týchto slov a z výsledkov Euklidovej vzdialenosti sa táto metóda použila pre rozpoznávač s tým, že sa pokúsi vylepšiť dvoma spôsobmi:

• výpočet Euklidovej vzdialenosti spektrogramov vypočítaných krátkou Fourierovou transformáciou s aplikáciou 3 okienok:
  • Blackman-Harris okienko,
  • Hammingove okienko – použité i doposiaľ,
  • pravouhlé okienko.
• výpočet Euklidovej vzdialenosti spektrogramov až po druhej redukcii pomocou aritmetického priemeru. [6]

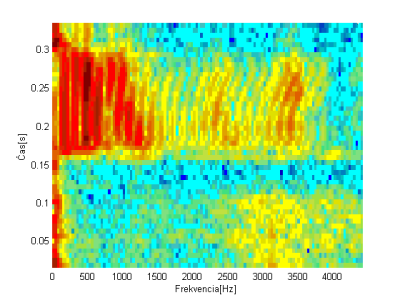
Použitie 3 okienok je vidieť na obr. 5. Priebeh spekra v čase je veľmi podobný. Najvyššia energia je do frekvencie 1500Hz v čase 0,15s až po koniec slova u všetkých troch použitých okienok. Rozdiely nie sú príliš veľké, ale od frekvencie 1500Hz v čase od 0,15s po koniec slova sú tam odlišnosti a preto i vypočítaná Euklidová vzdialenosť bude rozdielna.

(a)

(b)

(c)

Obr.5 Spektrogramy slova „stop” vysloveného rečníkom 1: a) s použitím Blackman-Harris okienka, b) s použitím Hammingového okienka a c) s použitím pravouhlého okienka

Na obr.6 môžeme vidieť výpočet druhej redukcie veľkosti spektrogramov pomocou aritmetického priemeru na Obr.6-b a Obr.6-e a výpočet Euklidovej vzdialenosti dvoch rozličných slov (obr.6-c) – slova „hore“-3 (obr.6-a) a „dole“-1 rečníka 4-žena.

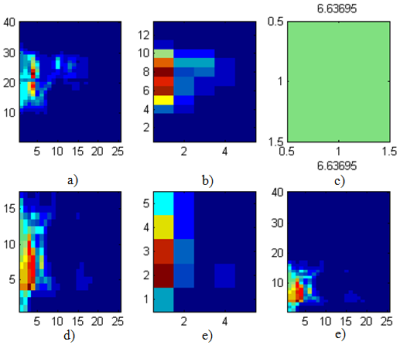
Obr.6 Porovnanie druhých redukcií spektrogramov slov “hore”-3 v hornom riadku a slova „dole“-1 vysloveného rečníkom 4 s Euklidovou vzdialenosťou

Záver

Porovnávanie spektrogramov pomocou Euklidovej vzdialenosti je veľmi jednoduchou možnosťou pri zníženom výpočtovom výkone. Vývojový systém FOX Board má len 100MHz procesor a pamäť RAM len 32MB. Takýto výkon je v dnešnej dobe nepostačujúci ( taktovacia frekvencia procesorov v mobilných telefónoch a tabletoch ďaleko presahuje 1GHz a použité sú pamäte 1GB a viac, nehovoriac o viacjadrových procesoroch). Z tohto hľadiska sa použitie spektrogramov s redukovanými maticami s použitím 3 okienok zdá ako dobré riešenie. Výsledky ukazujú veľkú Euklidovú vzdialenosť pri rôznych slovách a veľmi nízku pri rovnakých. Pri podobných slovách je táto vzdialenosť oveľa menšia ako pri celkom rôznych slovách. Testovanie tohto systému prebieha.

Poďakovanie

Článok vznikol vďaka podpore slovenského grantového projektu KEGA No. 005TUKE-4/2012.

Literatúra

1. Manual FOX Board, 28.10.2013,
   http://foxlx.acmesystems.it/
2. Hagiwara R., How to read a spectrogram, 7.4.2011,
   http://home.cc.umanitoba.ca/~robh/howto.html
3. Gurbuz, S. – Gowdy, J.N. – Tufekci, Z.:“ Speech spectrogram based model adaptation for speaker identification“, Proceedings of the IEEE Southeastcon 2000, ISBN: 0-7803-6312-4
4. Carmell, T.: “Spectrogram Reading”, 7.4.2011,
   http://cslu.cse.ogi.edu/tutordemos/SpectrogramReading/spectrogram_reading.html
5. Spectrograms and Wavelet Packets with Application to Automatic Stress and Emotion Classification in Speech“, ICICS 2009, IEEE, E-ISBN : 978-1-4244-4657-5
6. Bučko, R., Success rate of isolated words recognition by embedded system, In: Proceeding of scientific and student’s works in the field of Industrial Electrical Engineering, SSIEE – 2013, Vol. 2, Part 1, Technická univerzita v Košiciach, 2013, pp. 97-100, ISBN 978-80-553-1425-9