Optimalizácia 16-APSK modulácie pre SC-FDMA prenosové systémy

03. September, 2014, Autor článku: Dupák Denis, Elektrotechnika
Ročník 7, číslo 9 This page as PDF Pridať príspevok

p17330_iconTento príspevok je zameraný na zlepšenie prenosových vlastností SC-FDMA komunikačních systémov aplikáciou optimálnych 16-APSK modulácií v základnom pásme. V prvej časti práce je definovaná M-APSK modulácia a modely použitých nelineárnych zosilňovačov. V ďalšej časti sú opísané aplikované optimalizačné kritéria, podľa ktorých boli navrhnuté optimálne 16-APSK modulácie pre jednotlivé scenáre. V záverečnej časti článku sú prezentované prevádzkové vlastnosti navrhnutých16-APSK modulácií optimálnych podľa jednotlivých kritérií optimalizácie pre SC-FDMA komunikačné systémy.

1. Úvod

V súčasnosti prechádzajú bezdrôtové komunikačné systémy rýchlym rozvojom. Poskytovatelia komunikačných služieb, v snahe čo najviac uspokojiť požiadavky zákazníkov, poskytujú okrem telefonického spojenia aj širokú škálu iných služieb (internet, rozhlasový a televízny príjem, atď.). Zavádzanie týchto služieb je však spojené s nárastom požiadaviek na kapacitu komunikačných systémov. Jedným zo základných technologických riešení, ktoré sú v súčasnosti na riešenie tohto problému uvažované, je použitie širokopásmových bezdrôtových prenosových systémov s mnohonásobnými nosnými (MC, z angl. MultiCarrier), ktoré budú pracovať s vysokou energetickou (výkonovou) a spektrálnou účinnosťou[1].

V súčasnosti sú v praxi zavádzané mobilné komunikačné systémy 4. generácie, medzi ktoré patrí štandard LTE (z angl. Long Term Evolution) [2]. Tento štandard sa využíva na dve základné mnohoúčastnícke prístupy k prenosovému kanálu. Pre smer od základňovej stanice k účastníkovi (downlink) je použitá OFDMA (z angl. Orthogonal Frequency-division Multiple Access). Pre opačný smer (uplink) je v LTE definovaná metóda SC-FDMA (z angl. Single Carrier Frequency-division Multiple Access).

Zásadnou nevýhodou OFDM a SC-FDMA systémov je veľký pomer špičkového a priemerného výkonu signálu (PAPR, z angl. Peak to average power ratio), čo sa prejavuje značnou dynamikou fluktuácie obálky signálu. Tento efekt má za následok to, že koncové výkonové zosilňovače (HPA, z angl. High power amplifier) pracujú v nelineárnych častiach prenosových charakteristík, a tým dochádza k nelineárnemu skresleniu vysielaného signálu. Takáto degradácia vysielaného signálu sa prejavuje narastajúcou bitovou chybovosťou (BER, z angl. Bit error rate), ako aj vyžarovaním energie signálu do susedných frekvenčných pásiem [3].

Jedným z možných riešení ako znížiť dynamiku fluktuácie obálky SC-FDMA signálu je použitie vhodných modulácií v základnom pásme. Ako inšpiratívne riešenie v tomto prípade môže byť metodológia použitá v DVB-S2, kde bola ako modulácia v základnom pásme použitá 32-APSK modulácia. S cieľom zlepšiť prevádzkové vlastnosti SC-FDMA prenosových systémov s nelineárnymi HPA budeme sa v tejto práci zaoberať použitím optimálnych 16-APSK modulácií v týchto systémoch.

2. Definícia M-APSK

Konštelačný diagram M-APSK modulácie je tvorený množinou bodov, ktoré sú lokalizované na NR kružniciach (vo vzťahu ako kr.). Jednotlivé body sú lokalizované tak, že platia pre nich nasledujúce vzťahy [4]:

X = \left \{ \begin{array}{lll} r_1 exp[j((2 \pi / n_1)i + \theta_1)] & i=0, \dots , n_1 -1 & kr. \, l=1 \\ r_2 exp[j((2 \pi / n_2)i + \theta_2)] & i=0, \dots , n_2 -1 & kr. \, l=2 \\ M & M & M \\ r_{N_R} exp[j((2 \pi / n_{N_R})i + \theta_{N_R})] & i=0, \dots , n_{N_R} -1 & kr. \, l=N_R \end{array} \right . (1)

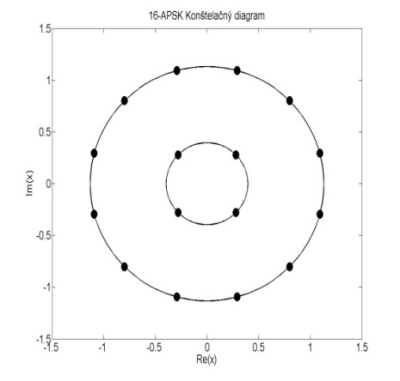
kde ni je počet bodov konštelácieležiacich na l-tej kružnici, ri je polomerl-tej kružnice a θi je relatívny fázový posun pre l-tú kružnicu (l= 1, …, NR). Takétokonštelácie sú označované ako n1 + n2 + … + nNR–APSK, kde n1 + n2 + … + nNR = M [5].Príklady konštelačných diagramov 16-APSK a 64-APSK sú zobrazené na obr.1.

p17330_01_obr01a

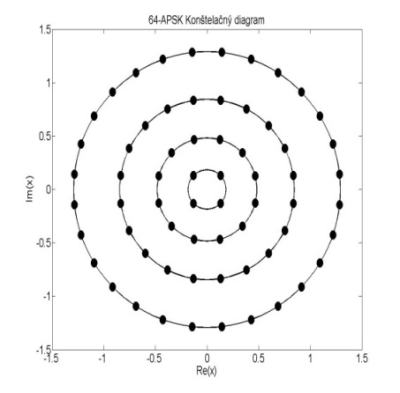
p17330_02_obr01b
Obr.1 Konštelačný diagram 16-APSK modulácie a 64-APSK modulácie

3. Analýza modulácií pre prípad nelineárnych kanálov

S cieľom identifikovania vhodných alternatívnych modulácií pre SC-FDMA komunikačné systémy sa v tejto časti budeme zaoberať 16-PSK a 16-QAM moduláciami. V ďalšej analýze sa budeme zaoberať vyšetrovaním vplyvu AWGN a nelineárneho skreslenia na 16-PSK SC-FDMA a 16-QAM SC-FDMA systémy. Kedže 16-PSK je modulácia s konštantnou obálkou signálu, je pravdepodobné, že 16-PSK modulácia bude v SC-FDMA prenosových systémoch menej citlivá na nelinearitu ako 16-QAM modulácia, ktorej obálka nie je konštantná. Naopak citlivosť 16-PSK modulácie na AWGN by mala byť väčšia ako v prípade 16-QAM modulácie, pretože Euklidovská vzdialenosť medzi konštelačnými symbolmi 16-PSK modulácie je menšia ako pri 16-QAM modulácii.

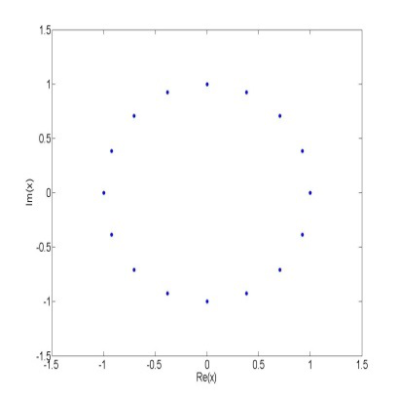
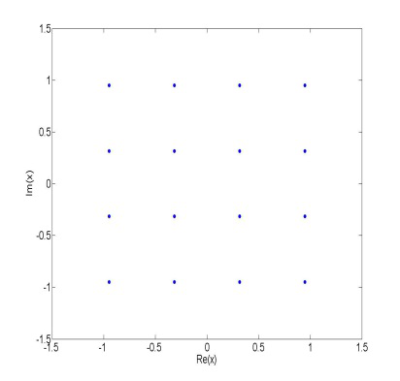
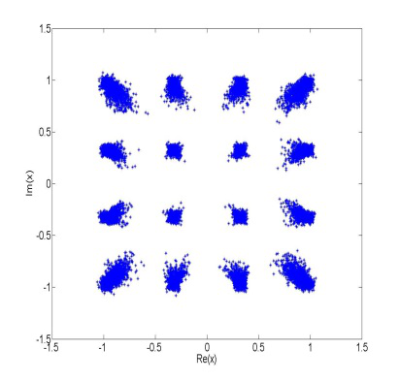
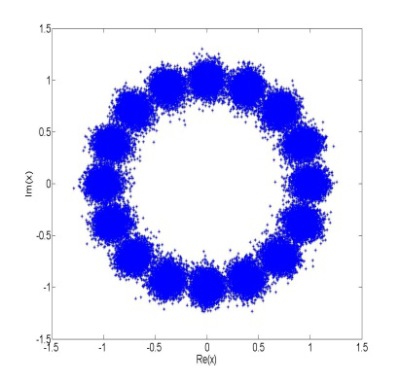
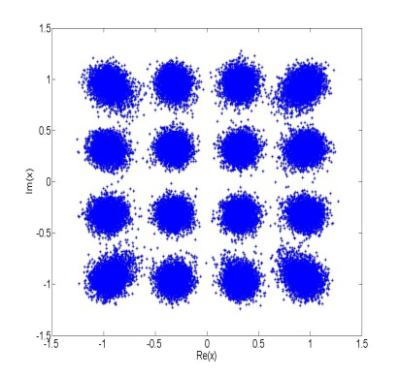
Konštelačné diagramy 16-PSK modulácie a 16-QAM modulácie sú na obr.2a a obr.3a. Konštelačné diagramy sú normované tak, že priemerný výkon dátového symbolu je rovný 1. Všetky konštelačné symboly, ktorých výkon je rovnaký, budú ležať na kružnici so stedom v počiatku súradnicovej sústavy s polomerom r, kde r2 je výkon konštelačného symbolu. Z obr.2a vidíme, že všetky komplexné dátové symboly 16-PSK sú rozložené na kružnici. Vzhľadom na to je zrejmé, že výkon všetkých symbolov 16-PSK modulácie je rovnaký. Z obr.3a je možné pozorovať, že výkony symbolov 16-QAM modulácie sú rôzne v závislosti od vzdialenosti symbolov od počiatku súradnicovej sústavy. Z uvedeného je zrejmé, že výkony symbolov pre 16-QAM moduláciu v provnaní s výkonmi symbolov M-PSK modulácie sa menia. Táto zmena výkonov vysielaných dátových symbolov má nežiadúci vplyv na chybovosť SC-FDMA prenosového systému.

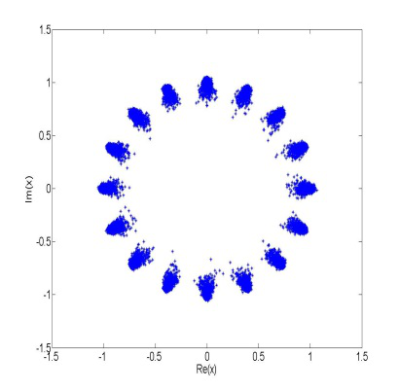
Z uvedených obrázkov možno pozorovať, že jednotlivé symboly na výstupe tejto časti prenosového reťazca už nie sú umiestnené v presných pozíciach bodov konštelačného diagramu, ale pretože dochádza k nelineárnemu skresleniu signálu, sú z týchto pozícií vychýlené. Ak je toto vychýlenie dostatočne veľké, dochádza k tomu, že Euklidovská vzdialenosť vychýleného symbolu od pôvodného bodu konštelačného diagramu je väčšia ako Euklidovská vzdialenosť k susednému bodu konštelácie, čo spôsobí chybnú detekciu v prijímači.Porovnaním modulácií 16-PSK a 16-QAM na obr.2b a obr.2bje možné pozorovať, že nelineárne skreslené 16-PSK symboly na výstupe SC-FDMA demodulátora v prijímači sú pri použití rovnakého modelu HPA vychýlené menej ako 16-QAM SC-FDMA symboly.

p17330_03_obr02a
(a)

p17330_04_obr02b
(b)

p17330_05_obr02c
(c)
Obr. 2 a) konštelačný diagram 16-PSK modulácie b) zobrazenie 16-PSK symbolov na výstupe SC-FDMA demodulátora v prijímači. Model HPA: Soft Limit s IBO=2 dB c) zobrazenie nelineárne skreslených a zašumených 16-PSK symbolov na výstupe SC-FDMA demodulátora v prijímači. Model HPA: Soft Limit, IBO=2 dB a AWGN Eb/N0=15 dB

p17330_06_obr03a
(a)

p17330_07_obr03b
(b)

p17330_08_obr03c
(c)
Obr. 3 a) konštelačný diagram 16-QAM modulácie b) zobrazenie 16-PSK symbolov na výstupe SC-FDMA demodulátora v prijímači. Model HPA: Soft Limit, IBO=2 dB c) zobrazenie nelineárne skreslených a zašumených 16-QAM symbolov na výstupe SC-FDMA demodulátora v prijímači. Model HPA: Soft Limit, IBO=2 dB a AWGN Eb/N0=15dB

4. Špecifikácia optimalizačných kritérií

4.1 Kritérium maximalizácie MED

Ako bolo spomínané v predcházajúcej stati, citlivosť modulácií v základnom pásme na AWGN vzrastá so zmenšujúcou sa Euklidovskou vzialenosťou medzi všetkými možnými dvojicami konštelačnými symbolmi. Túto citlivosť možno redukovať navrhnutím takej konštelácie, v ktorej bude Euklidovská vzdialenosť medzi všetkými možnými dvojicami konštelačných symbolov čo najväčšia. Pre minimálnu Euklidovskú vzdialenosť δmin medzi všetkými možnými dvojicami bodov konštelácie potom platí:

f_{MED} (\chi )= \delta_{min} = min_{\forall i} \{ min_{i \neq k} |a_i - a_k | \} (2)

Vychádzajúc zo vzťahu (2) možno kritérium maximálnej minimálnej Euklidovskej vzdialenosti vyjadriť matematicky takto:

max_{\rho , \theta} \{ min_{\forall i} \{ \delta_{min}^i \} \} (3)

kde sa maximalizuje MED výberom parametrov ρ a θ, ktoré špecifikujú rozloženie bodov konštelačného diagramu M-APSK modulácie v signálovom priestore.[6].

4.2 Kritérium maximalizácie MI

Vychádzajúc z [7] a [8] bolo ukázané, že pre vzájomnú mieru informácie príslušnej signálovej konštelácie χ platí:

f_{MI} (\chi ) = log_2 N - \frac{1}{N} \sum_{k=0}^{N-1} E \left \{ \right .
\left . log_2 \sum_{i=0}^{N-1} exp \left [ -\frac{E_S}{N_0} (|a_k + w - a_i|^2 - |w|^2) \right ] \right \} (4)

kde E{} je operátor strednej hodnoty, Es je energia symbolu, ai a ak sú symboly konštelácie, N je počet stavov modulácie a w je šum s normálnym rozdelením hustoty pravdepodobnosti a spektrálnou výkonovou hustotou N0 [7]. Maximalizáciou vzťahu (5.6) dostávame optimalizačné kritérium pre návrh konštelácie definované vzťahom:

max_{\rho , \phi} \{ f(\chi ) \} (5)

4.3 Kritérium minimalizácie BER

BER prenosového systému je definovaná jako pravdepodobnosť toho, že bit nie je správne prijatý. Odhad BER možno vyjadriť ako:

f_{BER} (\chi ) = BER( \chi ) = \frac{N_{err}}{N_{Tx}} (6)

kde Nerr je počet chybne detekovaných bitov v prijímači a NTx je celkový počet vyslaných bitov. Na základe vzťahu (6) je možné zformulovať kritérium optimalizácie M-APSK modulácie vyjádřené vzťahom:

min_{\rho , \theta}(BER) (7)

podľaktoréhosavolia parametre ρ a θ tak, že sa minimalizuje bitová chybovosť pre daný pomer Eb/N0.

5. Zhodnotenie výsledkov optimalizačného procesu

V tejto časti páce budú analyzované prevádzkové vlastnosti SC-FDMA prenosových systémov z hľadiska BER, v kterých budú použité optimálne 16-APSK navrhnuté v predchádzajúcich statiach práce. V tejto časti budeme na základe zvoleného optimalizačného kritéria používať tri rôzne optimálne 16-APSK, ktoré budeme rozlišovať označením optimalizačného kritéria v zátvorke ( 16-APSK (MED), 16-APSK(MI), 16-APSK(BER) ).

5.1 Lineárny model HPA

Na obr.4 je znázornený prehľad chybovostí optimálnych 16-APSK (BER,MI,MED) SC-FDMA a 16-QAM SC-FDMA pri použití lineárneho modelu HPA. Tak ako bolo predpokladané, najnižšiu bitovú chybovosť vykazuje 16-QAM SC-FDMA systém. Bitová chybovosť 16-APSK (MED) a 16-APSK (BER) je približne rovnaká pre všetky hodnoty Eb/N0

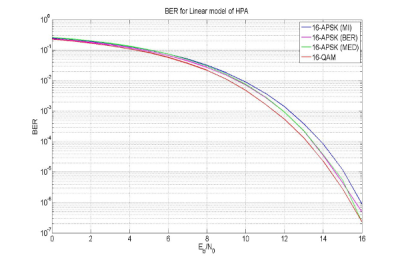
p17330_09_obr04
Obr. 4 BER SC-FDMA pri použití optimálnych 16-APSK (BER), 16-APSK (MI), 16-APSK (MED) a 16-QAM modulácií. Model HPA: lineárny model

5.2 Soft Limit model HPA

Na obr.5 sú znázornené BER krivky SC-FDMA penosového systému pri použití 16-APSK (BER,MI,MED) a 16-QAM modulácií. V tomto prípade bol použitý Soft Limit model HPA, IBO=2 dB. Ako je možné pozorovať z obr.5, aplikáciou 16-APSK (BER) bolo dosiahnuté výrazné zlepšenie bitovej chybovosti SC-FDMA systému. Zlepšenie BER 16-APSK (BER) modulácie v porovnaní s 16-QAM moduláciou je 4dB pri chybovosti 10-4. V prípade použitia optimálnej 16-APSK (MED) bolo dosiahnuté zníženie chybovosti v porovnaní s 16-QAM, avšak nie natoľko výrazné jako pri 16-APSK (BER). Optimálna 16-APSK (MI) vykazuje v porovnaní s 16-QAM vačku chybovosť, čo je spôsobené veľkými hodnotami Přerov polomerov kružníc ρ = r2/r1 optimálnej 16-APSK (MI).

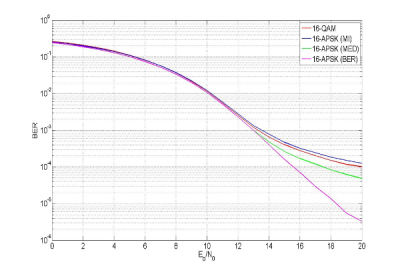
p17330_10_obr05
Obr. ‎5: BER SC-FDMA pri použití optimálnych 16-APSK (BER), 16-APSK (MI), 16-APSK (MED) a 16-QAM modulácií. Model HPA: Soft Limit model, IBO=2 dB

5.3 Rappov model HPA

Na obr.6 sú znázornené BER krivky 16-APSK (BER,MI,MED) a 16-QAM SC-FDMA systémov v nelineárnom kanáli typu Rapp, IBO=2 dB. Najnižšiu BER vykazuje 16-APSK (BER) SC-FDMA systém. Mierne zlepšenie chybovosti možno dosiahnuť aj použitím 16-APSK (MED) modulácie. Chybovosť 16-APSK (MI) SC-FDMA je aj v tomto prípade väčšia jako chybovosť 16-QAM SC-FDMA systému.

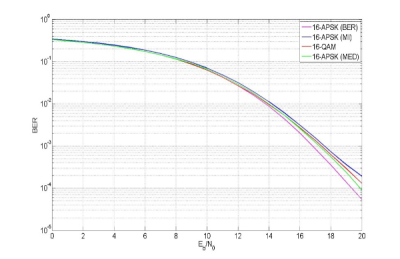
p17330_11_obr06
Obr. 6: BER SC-FDMA pri použití optimálnych 16-APSK (BER), 16-APSK (MI), 16-APSK (MED) a 16-QAM modulácií. Model HPA: Rappov model, IBO=2 dB

5.4 Salehov model HPA

Na obr.7 sú znázornené BER krivky SC-FDMA prenosového systému pri použití optimálnych 16-APSK (BER,MI,MED) a 16-QAM modulácií. Pre tento scenár bol použitý Salehov model HPA, IBO=2 dB. Z obr.7 je možné pozorovať, že najmenšiu chybovosť vykazuje 16-APSK (BER) SC-FDMA systém. Aj v tomto prípade sa neosvedčila aplikácia optimálnych 16-APSK (MED) a 16-APSK (MI), pričom použitím týchto modulácií v SC-FDMA prenosovom systéme bolo dosiahnuté iba mierne zlepšenie chybovosti SC-FDMA systému.

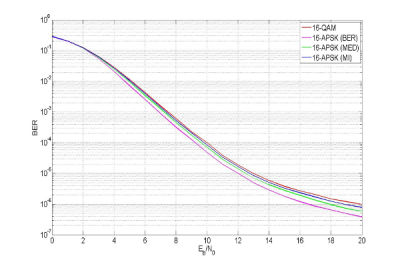
p17330_12_obr07
Obr. 7: BER SC-FDMA pri použití optimálnych 16-APSK (BER), 16-APSK (MI), 16-APSK (MED) a 16-QAM modulácií. Model HPA: Salehov model, IBO=2 dB, konvolučnýkóder 2/3

5.5 Optimálne modulácie pre rôzny počet subnosných

Optimalizačný proces bol vykonávaný za presne stanovených podmienok SC-FDMA penosového systému. S cieľom zistiť vlastnosti navrhnutej optimálnej 16-APSK modulácie v SC-FDMA systémoch s odlišnými nastaveniami, bola vykonaná analýza optimálnych 16-APSK SC-FDMA systémov s rôznym počtom subnosných.

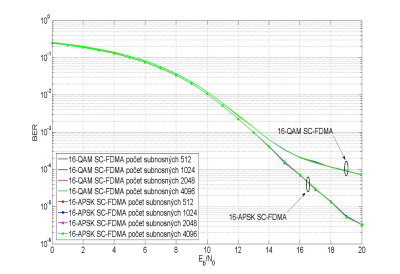
p17330_13_obr08
Obr. 8: BER 16-APSK SC-FDMA a 16-QAM SC-FDMA s rôznym počtom subnosných. Model HPA: Soft Limit, IBO=2 dB

Na obr.8 sú znázornené BER krivky optimálnych 16-APSK SC-FDMA a 16-QAM SC-FDMA prenosových systémov. Chybovosť 16-QAM SC-FDMA je vo všetkých prípadoch rovnaká, čo potvrzuje všeobecne známu vlastnosť SC-FDMA systémov, a to, že chybovosť SC-FDMA systému sa při zmene počtu subnosných nemení. Z obr.8 možno pozorovať, že pri použití optimálnych 16-APSK je táto vlastnosť SC-FDMA systémov zachovaná a BER 16-APSK SC-FDMA je tiž rovnaká pre rôzne počty subnosných. Toto zistenie je z hradiska použitia optimálnych 16-ASPK modulácií veľmi dôležité, keďže aplikácia navrhnutých optimálnych 16-APSK moduláciínie je striktne obmedzená na SC-FDMA prenosové systémy s 512 subnosnými, ktoré boli použité v optimalizačních procesoch.

6. Záver

Navrhnuté optimálne 16-APSK vykazujú lepšie prevádzkové vlastnosti v porovnaní s 16-QAM moduláciou pre SC-FDMA prenosové systémy, ak bol použitý nelineárny model HPA. V prípade lineárneho modelu HPA síce 16-QAM dosahuje nižšiu bitovú chybovosť ako optimálne 16-APSK modulácie, ale v praxi situácia, kde je prevodová charakteristika HPA lineárna, v podstate nenastáva. Z tohto dôvodu je pre praktické použitie výhodné aplikovať optimálne 16-APSK modulácie do prenosového reťazca SC-FDMA systému. Keďže optimalizačný proces bol vykonaný takým spôsobom, že boli navrhnuté optimálne 16-APSK modulácie pre zvolený model HPA a stanovený pomer Eb/N0, tak vhodným spôsobom pre implementáciu optimálnych 16-APSK modulacií do praxe je adaptívna 16-APSK modulácia, ktorá by na základe získaných informácií o aktuálnom stave v prenosovom kanáli vybrala optimálnu 16-APSK moduláciu pre tento stav.

Zoznam použitej literatúry

  1. Hara, S., Prasad, R.: Multicarrier Techniques for 4G Mobile Communications. Boston: ArtechHouse, 2003.
  2. 3GPP TSG RAN WG1, TDoc R1-060023, Cubic Metric in 3GPP-LTE, Jan. 2006
  3. Herraiz, D.M.: On OFDM-based multicarrier communication systems with low sensitivity to nonlinear amplification, Thesis for the Advanced Studies Diploma. Barcelona: Ramon Llull University, 2006
  4. Liolis, K.P., Alagha, N.S.: On 64-APSK constellation design optimization. In: Signal Processing for Space Communications, 2008. SPSC 2008. 10th International Workshop, 6-8 Oct. 2008, pp. 1,7.
  5. Liolis, K. P. et al.: Amplitude PhaseShift Keying Constellation Design and its Applications to Satellite Digital Video Broadcasting. In: DE RANGO, Floriano: Digital Video. Croatia : Intech, February 2010, p. 425-452.
  6. Ungerboeck, G.: Channelcoding with multilevel phase signals. IEEE Transactions on Information Theory , vol. 28, no.1, 1982, pp. 55–67.
  7. Shannon, C.E.: Communication in the Presenceof Noise, Classic Paper1948.
  8. Gaudenzi, R.De., Fabegas, A.G. and Matinez, A.: Performance Analysisof Turbo-Coded APSK Modulations over Nonlinear Satellite Channels. IEEE Transactions on Wireless Communications, vol. 5, no. 9, 2006.
Spoluautorom článku je Dušan Kocur

Napísať príspevok