Článok sa zaoberá skúmaním SBS (angl. Stimulated Brillouin Scattering), ktorý patrí medzi dominantné nelineárne javy v optike. Výskum v tejto oblasti je v súčasnosti veľmi aktuálny. Snahy v súkromnom aj verejnom sektore sú zamerané na prenos čo najvačšieho množstva dát na čo najväčšie vzdialenosti. Hlavná pozornosť je venovaná vplyvu SBS na WDM plne optické komunikačné systémy. Praktické overenie vplyvu SBS je uskutočnené v simulačnom prostredí Optsim.

1. Úvod

Problémy s narastajúcimi požiadavkami na šírku prenosového pásma rieši plne optický komunikačný systém. Jadrom optických komunikačných systémov je optické vlákno, v ktorom sa šíri signál rýchlosťou svetla. V súčasnosti sa jedná o najstabilnejší a najrýchlejší spôsob prenosu dát, ale zároveň aj cenovo najnedostupnejší. Optický komunikačný systém sa využíva najmä v chrbticovej sieti, a to práve preto, že sú tam najväčšie požiadavky na šírku prenosového pásma. Aj keď v súčasnosti sa už optika tlačí ku koncovým používateľom. Prenos optickým komunikačným systémom patrí medzi najstabilnejšie. Aj tieto systémy majú nepriaznivé efekty, ktoré vznikajú pri prenose signálu cez optické vlákno. Práve jedným nelineárnym javom sa táto práca zaoberá a to konkrétne stimulovaným Brillouinovým rozptylom (SBS).

2. Stimulovaný Brillouinov rozptyl

Stimulovaný Brillouinov rozptyl (SBS) je nelineárny proces, ktorý sa môže vyskytovať v optických vláknach a ktorého prahová hodnota je oveľa nižšia ako u SRS. Prekročenie prahovej hodnoty má za následok generovanie spiatočnej Stokesovej vlny, ktorá nesie väčšinu príkonu (vstupného výkonu). Z toho dôvodu SBS obmedzuje výkon kanála v optických komunikačných systémoch. Avšak tento jav je možné užitočne využiť a to pre výrobu optických Brillouinovych zosilňovačov a Brillouinovych laserov. Táto kapitola sa zaoberá SBS v optických vláknach. V podkapitole 2.1 sa uvádzajú základne pojmy (vlastnosti, princípy) s dôrazom na spektrum Brillouinovho zisku.

2.1 Základné pojmy

Nelineárny jav SBS bol prvýkrát pozorovaný v roku 1964 a následné aj študovaný. SBS sa prejavuje prostredníctvom generovania Stokesovych vĺn, ktorých frekvencia je posunutá smerom dole od dopadajúceho svetla a to o hodnotu, ktorá je závislá od nelineárneho média. Nelineárny jav SBS je podobný javu SRS, kvôli tomu si uvedieme hlavné rozdiely medzi týmito dvoma javmi. Prvý rozdiel medzi SBS a SRS je taký, že Stokesová vlna v SRS sa šíri v oboch smeroch a v SBS len spiatočným smerom v prípade jednovidových vlákien. Stokesové posunutie (prib ižne GHz) je menšie o tri rady pre SBS v porovnaní s SRS (približne 13 THz). Prahová hodnota výkonu čerpadla pre SBS závisí od spektrálnej šírky súvisiacej s čerpadlovou vlnou. Táto hodnota môže byť na úrovni aj 1 mW pre CW čerpadlo, alebo keď čerpadlo je vo forme relatívne širokých impulzov (šírka > 1 µs).

V kontraste, SBS takmer nevzniká v prípade krátkych impulzov čerpadla (šírka < 1 ns). Pre porovnanie prahová hodnota výkonu u SRS je približne 0,5 W. Na druhej strane, koeficient Brillouinovho zisku je 100-krát väčší ako pri Ramanovom zosilnení, čo vytvára SBS dominantným nelineárnym javom v kremíkových vláknach za určitých okolností. To platí hlavne v prípade optických systémov, ktoré používajú lasery s úzkou šírkou čiary (narrow-linewidth). Všetky tieto rozdiely vychádzajú z jedného hlavného rozdielu a to: akustické fonóny sa podieľajú v SBS zatiaľ čo optické fonóny sú zapojené v prípade SRS [1].

2.1.1 Fyzikálny proces (princíp)

Proces SBS môže byť opísaný ako nelineárna interakcia medzi čerpacím, Stokesovým pólom a akustickou vlnou. Akustická vlna je generovaná prostredníctvom procesu elektrostrikcie. Elektrostrikcia je jav inverzný k piezoelektrickému javu, čiže je to zmena objemu alebo tvaru nevodičov vplyvom vonkajšieho elektrického poľa. Čerpacia vlna vytvára tlakovú vlnu v médiu prostredníctvom elektrostrikcie. Materiálová hustota stanovuje, že vlna sa šíri rýchlosťou zvuku v médiu v smere čerpacej vlny, čiže vzniká akustická vlna. Následne akustická vlna produkuje hustú moduláciu, čo má za následok moduláciu indexu lomu média. Periodické zmeny materiálovej hustoty vlákna sa javia ako pohybujúci sa index lomu mriežky. Čiže čerpadlo stimuluje indexovú mriežku čo zapríčiňuje rozptyl svetla čerpadla prostredníctvom Braggovej difrakcie.

Značná časť optického výkonu čerpacej vlny môže byť prevedená na Stokesovú vlnu, ktorá smeruje v spätnom smere. Rozptýlené svetlo je tiež frekvenčne posunuté smerom nadol a to pre Dopplerov posun, ktorý súvisí s mriežkovým pohybom akustickej rýchlosti. Tento proces je schematicky znázornený na Obr. 1. Reakcia materiálu na interferenciu čerpadla a Stokesovho poľa vedie k zvýšeniu amplitúdy akustickej vlny. Na druhej strane, impulz (beating) čerpacej vlny s akustickou vlnou má tendenciu posilňovať Stokesovú vlnu. To vysvetľuje vzhľad procesu stimulovaného Brillouinovho rozptylu. Rovnaký proces rozptylu je možné vidieť v kvantovej mechanike ako zánik čerpadlových fotónov, z ktorých sa vytvoria Stokesové fotóny a akustické fonóny súčasne. Keďže obe energie a hybnosti musia byt zachované počas každého rozptylu, tak frekvencie a vlnové vektory troch vĺn sú zviazané a to vzťahmi:

(1)

(2)

kde ω_P a ω_S sú frekvencie, k_p a k_S sú vektory čerpadlových vĺn a Stokesových vĺn [18][19].

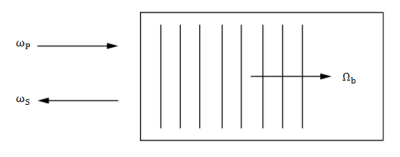
Obr. 1 Schematická ilustrácia SBS procesu

Frekvencia Ω_B a vektor vlny k_A z akustickej vlny spĺňajú štandard disperzného vzťahu

(3)

kde θ je uhol medzi čerpadlom a Stokesovým pólom, a z rovnice (2) sme predpokladali |k_p|≈|k_s|. Rovnica (3) vyjadrujeposun frekvencie o Stokesovú vlnu závislú od uhla rozptylu. Hlavne v prípade, keď Ω_B je maximálne a to v spätnom smere (θ=π) a s nulovou (zanedbateľnou) hodnotou v priamom smere (θ=0). V jednovidovom optickom vlákne sú podstatné len priamy a spätný smer. Z toho dôvodu SBS nastáva len v spätnom smere s Brillouinovým posunom, ktorý má hodnotu

(4)

kde z rovnice (3) bolo použité |k_p|=(2πn_p)⁄λ_p ,kde λ_p je vlnová dĺžka čerpacej vlny a n je index lomu vlákna. Ak použijeme hodnoty v_A=5,96 km/s a n_p=1,45, čo sú typické hodnoty pre kremíkovévlákno, dosiahneme Brillouinov frekvenčný posun v_B≈11,5 GHz pri λ_p=1,55 μm [19].

Aj napriek tomu, že rovnica (3) predpokladá správne, že k SBS by malo dôjsť len v spätnom smere u jedno-vidových vlákien (single-mode fibers – SMFs), avšak spontánny Brilloinov rozptyl môže nastať aj v priamom smere. Malé množstvo Stokesovho svetla je generované v priamom smere. Tento jav sa označuje ako „riadená akustická vlna“ (guided-acousitc-wave) Brillouinovho rozptylu. V praxi Stokesove spektrumznázorňuje viacnásobne čiary s posunutou frekvenciou v rozsahu od 10 do 1000 MHz. Vzhľadom k extrémne zriedkavému výskytu(a slabej povahe) tento jav nebude rozoberaný v tejto práci [2].

2.2.1 Spektrum Brillouin-ovho zisku

Nárast Stokesovej vlny je charakterizovaný ziskom Brillouinovho spektra g_B(Ω), vrcholom v Ω=Ω_B. V porovnaní s SRS je spektrálna šírka Brillouinovho ziskového spektra veľmi malá (približne 10 až 100 MHz namiesto 10 THz), pretože sa vzťahujek dobe tlmenia akustických vĺn v súvislosti s životnosťou fonónov. V prípade, keď akustická vlnasa exponenciálne utlmuje(tlmí), čiže exp(-Γ_B t), tak Brillouinov zisk ma Lorentzové spektrum v tvare

(5)

kde špičková hodnota Brillouinovho zisku v Ω=Ω_B je daná

(6)

kde, ρ₀≈2210 kg/m³ je hustota materiálu, Γ_B je fenomenologický koeficient tlmenia, γ_e≈0,902 je elektrostrikčná (electrostrictive) konštanta kremíka (silica), a f_A je frakcia, ktorá redukuje SBS zisk, ak akustické a optické vidy sa plne neprekrývajú vo vnútri vlákna. Plná/celá šírka v polovičke maxima (full width at half maximum (FWHM)) zisku spektra je vztiahnutá k Γ_B a to vzťahom ∆v_B=Γ_B/(2π). Životnosť fonónu T_B=Γ_B^-1, je typická <10 ns [2, 3].

Merania Brillouinovho zisku vo väčšine kremíka boli už vykonané v roku 1950. Meraniami vykonanými v roku 1979 s argón-iónovým laserom boli zistené tieto hodnoty v_B=34,7 GHz, ∆v_B=54 MHz, a λ_p=486 nm, pričom ∆v_B je šírka Brillouinovho spektra. Tieto experimenty tiež ukazujú, že ∆v_B závisí na Brillouinovom posunutí a mení sa o niečo rýchlejšie ako v_B²; kvadratická závislosť sa berie ako predpoklad z teórie. Z rovnice (4) je zrejme,že v_B sa mení nepriamo s λ_p, čiže ∆v_B následne závisí na vlnovej dĺžke čerpadla λ_p^-2.Zužovanie profilu Brillouinovho zisku s narastajúcim λ_p, ruší pokles Brillouinovho zisku vychádzajúceho z rovnice (6).

Na základe toho môžeme tvrdiť, že špičková hodnota g_p je takmer nezávislá od vlnovej dĺžky čerpadla. Ak typické hodnoty parametrov kremíkového vlákna sú použité v rovnici (6), tak g_p sa pohybuje v rozsahu 3-5*10^-11 m/W. Pre porovnanie táto hodnota je väčšia takmer o tri rady v porovnaní s Ramanovým koeficientom zisku. U niektorých nie kremíkových vlákien môžu byť väčšie hodnoty koeficientu Brillouinovho zisku. Pre príklad u telluričitanových (tellurite) vlákien bola zistená špičková hodnota 1.6989×10^-10 m/W. Druhý príklad je pre jednovidové As₂ Se₃ chalkogenidové (chalcogenide) vlákna, kde sa namerala hodnota približne 6.08×10^-9 m/W čo je viac ako 200 krát väčšia hodnota ako u kremíkových vlákien [3].

Spektrum Brillouinovho zisku pre kremíkové vlákno sa môže výrazne líšiť od väčšej časti kremíka a to z dôvodu sprevádzaných vlastností optických vidov a prítomnosti dopantov (zmesí) v jadre vlákna. Na Obr. 2 môžeme vidieť zisk spektra nameraného pre tri rôzne vlákna s rôznymi štruktúrami a rôznymiúrovňami dopovania germánia (GeO₂) v ich jadrách. Merania boli vykonané použitím external-cavitypolovodičovým laserom pracujúcim na vlnovej dĺžke 1,525 μm a použitím technikyheterodynovej detekcie (heterodyne-detection) s 3-MHz rozlíšením. Krivka a na Obr. 2 predstavuje vlákno s jadrom blízkym čistému kremíku (GeO₂ koncentrácia o 0,3%/mole). Nameraný Brillouinov posun v tomto vlákne bol v_B≈11,25 GHz, ktorý je v súlade s rovnicou (4), ak použijeme akustickú rýchlosť väčšiny kremíka. Pre vlákna reprezentujúce krivky (b) a (c) je Brillouinov posun redukovaný s takmer inverznou závislosťou na koncentrácií GeO₂. Vlákno (b) má štrukúru dvojitej špičky, ktorá vyplýva nehomogénnemu rozloženiu GeO₂ vo vnútri vlákna [3, 4].

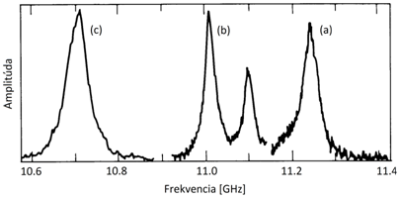
Obr. 2 Brillouinov zisk spektra troch vlákien pre vlnovú dĺžku λ_p=1,525 μm a to pre (a) vlákno z kremikového vlákna, (b) vlákno so slabším plášťoma (c) vlákno s posunutou disperziou [2]

Viac súčasných meraní ukazuje, že spektrum Brillouinovho zisku závisí značne na detailoch návrhu/konštrukcií vlákna a môže obsahovať viacnásobné špičky, ktoré majú pôvod v rôznych akustických vidochpodporovaných vláknami. Troj-špičkový zisk (three-peak-gain) spektra bol spozorovaný už v roku 1988 a interpretovaný ako výsledok z rôznych akustických rýchlosti v jadre a oblastiach plášťa vo vlákne. V experimente v roku 2002, bol zisk spektra zaznamenaný pre štyri druhy vlákien odlišných nie len v rozmere jadra, ale aj v úrovni dopovania GeO₂ vo vnútri jadra (v rozmedzí od 3,6% do 20%). Zisk spektra vykazoval až päť špičiek v závislosti od konštrukcie vlákna. Brillouinov posun spojený s dominantnou špičkou sa tiež mení od 9 do 11 GHz, menšie hodnoty frekvenčného posunu sa získavajú pre vlákna s väčšou koncentráciou GeO₂.

Napríklad na Obr. 10 môžeme vidieť zisk spektra nameraného pre disperzne kompenzované vlákno (dispersion-compensating fiber DCF) s 18% GeO₂ v niekoľkých výkonových úrovniach čerpadla. Dominantná špička sa nachádza na frekvenčnom posune 9,77 GHz, ale štyri menšie špičky sú tiež jasne viditeľné na vyšších frekvenciách. Tieto špičky zodpovedajú rôznym akustickým režimom vlákna,pretože každý vid ma inú akustickú rýchlosť v_A, na základe čoho má taktiežrôzny Brillouinov posun, ako je uvedené v rovnici (4). Zmeny v zisku spektra pri vysokých výkonoch čerpadla súvisia s nábehom SBS. Zistilo sa tiež, že nad prahovou hodnotou stimulovaného rozptylu sa zvyšuje iba výkon hlavného vrcholu s rastúcim vstupným výkonom, zatiaľ čo ostatné rezonančné vrcholy sa znižujú až nakoniec zmiznú [3, 5].

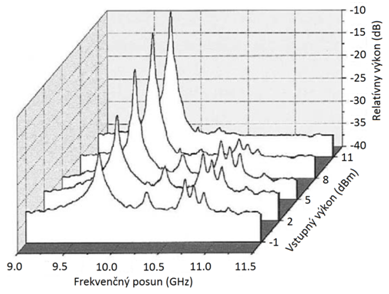
Obr. 3 Spektrum Brillouinovho zisku disperzie kompenzačného vlákna pre päť úrovní vstupného výkonu pri vlnovej dĺžke λ_p=1,525 μm [4]

Šírka pásma špičkydominantného zisku na Obr. 9 a Obr. 10 zodpovedá šírke pásma Brillouinovho zisku ∆v_B a súvisí so životnosťou fonónu. Čo je oveľa viac ako sa očakávalo od väčšiny kremíka (∆v_B≈17MHz pri λ_p=1,525 μm). Ďalšie pokusy tiež potvrdili podobné výsledkya to veľkú šírku pásma Brillouinovho zisku pre vlákna na báze kremíku. Časť nárastu šírky pásma je spôsobená vlastnosťami akustických vidov v optických vláknach. Najväčší nárast môžeme pripísať nehomogenitám v priereze jadra vlákna pozdĺž celej dĺžky vlákna. Numerická apertúra vlákna zohráva tiež úlohu v rozložení SBS zisku spektra. Keďže tieto faktory sú špecifické pre každé vlákno, tak ∆v_B je hlavný rozdiel pre rôzné vlákna a môže prekročiť 100 MHz v 1,55 μm oblasti spektra [4, 6].

Rovnica (5) pre Brillouinov zisk je získaná za ustálených podmienok a je platná pre CW (continuous-wave) alebo quasi-CW (kvázi-CW) čerpadlo (šírka pulzu T₀ ≫ T_B), ktorého spektrálna šírka ∆v_p je oveľa menšia ako ∆v_B (T₀ je šírka pulzu, T_B je životnosť fonónu). Pre čerpadlo s impulznou šírkou T₀ < T_B, je Brillouinov zisk podstatne znížený v porovnaní so ziskom získaným z rovnice (6). Ak šírka pulzu bude oveľa menšia ako životnosť fonónu (T₀ < 1ns), potom Brillouinov zisk je redukovaný pod Ramanovo zosilnenie.

Aj v prípade CW čerpadla je spektrum Brillouinovho zisku značne rozšírené, ak spektrálna šírka čerpadla ∆v_p prekročí ∆v_B. Táto situácia môže nastať v prípade, keď je použitý mnoho-vidový laser pre čerpanie. Taktiež táto situáciamôže nastať pre čerpanie u jedno-vidového lasera, ktorého fáza sa rýchlejšie mení v čase ako je životnosť fonónu T_B. Podrobné výpočty ukazujú, že Brillouinov zisk, za podmienok širokopásmového čerpania, závisí od relatívnej veľkosti dĺžky koherencie čerpadla, definovanej L_coh=c/(n_p ∆v_p) a dĺžky SBS-interakcie L_int definovanej ako vzdialenosť, počas ktorej sa značne mení Stokesová amplitúda. Ak L_coh ≫ L_int, proces SBS je nezávislý na vidovej štruktúre čerpadla lasera za predpokladu, že vidový priestor prevyšuje ∆v_B a Brillouinov zisk je skoro rovnaký ako pre jedno-vidový laser po niekoľkých interakčných dĺžkach. Naopak, Brillouinov zisk je výrazne znížený ak L_coh ≪ L_int. Posledná spomenutá situácia je všeobecne aplikovateľná pre optické vlákna, kde interakčná dĺžka je porovnateľná s dĺžkou vlákien L, kde straty vlákien nie sú príliš veľké [3].

Efektívny Brillouinov zisk g_B^eff (ω_s) pre širokopásmové CW čerpadlo možno získať integrovaním Brillouinovho zisku spolu so spektrom čerpadla S_p (ω_p). Avšak zisk SBS je sprevádzaný zmenami v indexe lomu a musíme použiť komplexnú formu g_c zisku spektra, ktorého reálna časť poskytuje zisk SBS:

(7)

kde S_p (ω-ω^p) je normalizované tak, že . V prípade čerpadla lasera s Gaussovým spektrom šírky ∆ω_p, spektrum čerpadla má tvar

(8)

Vykonanie integrácie v zmysle doplňujúcej chybovej funkcie vzťahu (7) dostaneme

(9)

kde p=(Ω_B+ω_s-ω_p)/∆ω_p a q=Γ_B/(2∆ω_s) sú dve bezrozmerné čísla. Ak zoberieme, že g_B=Im(g_c), tak dostaneme

(10)

Ak q≪1, zisk Brillouinovho spektra sa stáva skoro gausovským a má rovnakú šírku ako spektrum čerpadla, tzn. že je rozšírené faktorom o(2∆ω_p)/Γ_B, a súčasne špička hodnoty zisku je znížená rovnakým faktorom. To je dôvod prečo prah SBS narastá veľkým faktorom keď ∆ω_p ≫ Γ_B [3, 7].

3. Experimentálne výsledy

Na overenie vplyvu SBS bola zhotovená schéma zobrazená na Obr. 4. Jedná sa o jednoduchú schému, ktorá pozostáva z CW lasera, optického zosilňovača, a dvoch optických vlákien (poprípade viac) a meracích jednotiek. Schéma bola zostavená v blokovom režime Optsimu. Z uvedenej schémy je zrejme, že vysielaný optický signál nie je modulovaný. Čiže sa jedná o čistý signál z CW laseru, ktorý je zosilnený optickým zosilňovačom. Po optickom zosilňovači signál putuje do optických vlákien, z ktorého jedno vlákno uvažuje s vplyvom SBS a druhé vlákno bez vplyvu SBS. Na koncoch sa nachádzajú len meracie jednotky.

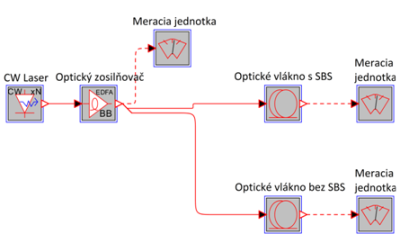
Obr. 3 Simulačná schéma na overenie vyplyvu SBS

Na Obr. 4 sú porovnané hodnoty z výstupu optického zosilňovača (Obr. 4(a)), s hodnotami z výstupu optického vlákna bez uvažovania SBS vplyvu (Obr. 4(b)). Hodnoty z optického zosilňovača predstavujú vstupný výkon. Ako môžeme vidieť hodnoty z Obr. 4(b)tak oproti Obr. 4(a) sú konštantne nižšie a to vplyvom útlmu optického vlákna (na dĺžku 50 km to je celkový útlm 12.5 dB). Ostatné nelineárne vplyvy boli obmedzené a to z dôvodu čo najväčšej viditeľnosti zmien vplyvom SBS.

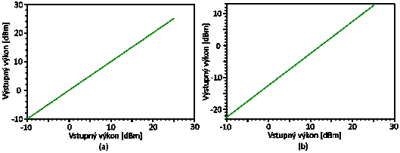
Obr. 4(a) Závislosť výstupného výkonu od vstupného výkonu za optickým zosilňovačom (b) závislosť výstupného výkonu od vstupného výkonu na výstupe optického vlákna bez uvažovania SBS javu

3.1 Vplyv zmeny vysielacieho výkonu na SBS jav

Najväčším vplyvom na SBS jav je vysielací výkon (naviazaný výkon v optickom vlákne), tzn. udržaním vysielacieho výkonu pod prahovou hodnotou najviac limitujeme vplyv SBS javu. Zmenou vysielacieho výkonu optického signálu môžeme sledovať ako sa mení výkon optického signálu na výstupe optického vlákna a to vplyvom SBS javu (Obr. 5). Rozdiel medzi výstupným výkonom vlákna, bez uvažovania SBS a s uvažovaním SBS, predstavuje spätne šíriacu sa SBS vlnu posunutú o hodnotu, ktorú je možné nastaviť vo vlákne (zisk SBS). Avšak parametre, ako je posun a šírka SBS vlny, nebudeme meniť, keďže to ovplyvňuje celý komunikačný systém, ale neovplyvňuje prahovú hodnotu. Závislosťou výstupného výkonu na vstupnom výkone je možné určiť prahovú hodnotu SBS javu. Prahová hodnota pri predvolených parametroch SBS uvedených vyššie vychádza okolo 12.8 dBm vstupného výkonu a výstupný výkon pri tejto hodnote nadobúda približne 0.07 dBm. Pre porovnanie výstupný výkon z optického vlákna bez uvažovania SBS nadobúda približne 0.3 dBm, čo je rozdiel 0.23 dBm. Pri vstupnom výkone 20 dBm je rozdiel dokonca až 19 dBm.

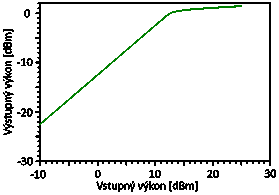
Obr. 5 Závislosť výstupného výkonu na vstupnom výkone pri uvážení SBS javu pri štandardných hodnotách parametrov

Na základe prahovej hodnoty sa bude rozlišovať veľkosť zmeny vplyvu SBS javu podľa zmien meniacich parametrov.

3.2 Vplyv polarizácie optického vlákna na SBS jav

Polarizáciou vlákna je možné dosiahnuť posun prahovej hodnoty, a to buď k vyšším alebo nižším hodnotám posunu. Samozrejme žiadanejšie sú vyššie prahové hodnoty SBS. Na Obr. 6 je možné porovnať závislosti výstupných výkonov od vstupných, pri dvoch rôznych stavoch polarizácie optického vlákna. Na Obr. 6(a) je závislosť pri polarizácií o hodnote 1.1 a na Obr. 6(b) je pri hodnote 1.9. Hodnota polarizácie 1.0 znamená maximálne depolarizované optické vlákno, avšak v praxi takáto situácia nenastáva, z toho dôvodu sa vykonala simulácia pri hodnote 1.1. Podobne polarizácia o hodnote 2.0 je ideálna polarizácia vlákna, čo v praxi je ťažko realizovateľné, preto bola použitá hodnota 1.9. Závislosť pri hodnote polarizácií 1.5, čo je typická hodnota polarizácie, je znázornená na Obr. 5. Prahové hodnoty pri hodnotách 1.1, 1.5 a 1.9 polarizácie sú uvedené v Tab. 1, ako aj rozdiely oproti typickej hodnote polarizácie. V Tab. 1 je možné si všimnúť, že pri depolarizácií vlákna je menší rozdiel posunu prahovej hodnoty ako pri polarizácií optického vlákna.

Tab. 1 Prahové hodnoty a ich rozdiel oproti predvolenej hodnote pri polarizácií optického vlákna

Hodnota polarizácie vlákna	Prahová hodnota [dBm]	Rozdiel oproti predvolenej hodnote [dBm]
1.1	11.2	-1.6
1.5	12.8	–
1.9	15	2.2

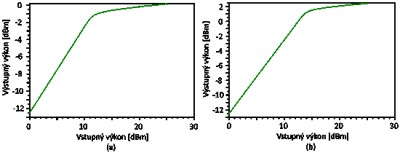
Obr. 6 Závislosť výstupného výkonu na vstupnom výkone pri hodnote polarizácie (a) 1.1, a pri hodnote (b) 1.9

3.3 Vplyv priemeru jadra optického vlákna na SBS jav

Ďalší parameter, ktorý ovplyvňuje prahovú hodnotu SBS je priemer jadra vlákna. V Tab. 2 sú uvedené priemery jadra vlákna a ich prahová hodnota, pre ktoré boli vykonané simulácie. Výsledky zo simulácií sú zobrazené na Obr. 7. Priemer jadra vlákna o hodnote 6 μm je zobrazený na Obr. 7(a), pre priemer 8.2 μm naObr. 7(b), pre priemer 9.2 μm (Obr. 7(c)) a pre hodnotu 10.4 je na Obr. 7(d). Z Tab. 2 je možné vyčítať, že prahová hodnota sa mení lineárne a to 1 dB na 1 μm. Pri väčšom priemere jadra je vyššia prahová hodnota.

Tab. 2 Prahové hodnoty a ich rozdiel oproti predvolenej hodnote pri závislosti od priemeru jadra optického vlákna

Priemer jadra optického vlákna [μm]	Prahová hodnota [dBm]	Rozdiel oproti predvolenej hodnote [dBm]
6	9.8	-3
8.2	12.8	–
9.2	13.6	0.8
10.4	14.8	1.2

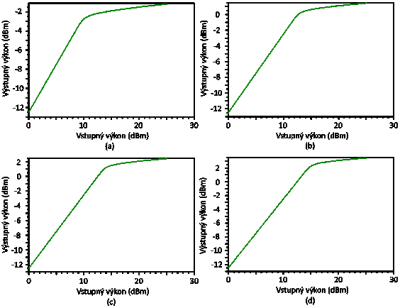
Obr. 7 Závislosť výstupného výkonu na vstupnom výkone pri priemeru optického vlákna (a) 6 μm, (b) 8.2 μm, (c) 9.2 μm a (d) 10.4 μm

3.4 Vplyv vlnovej dĺžky na SBS jav

Ako posledný parameter, pri ktorom sme sa sústredili na zmenu prahovej hodnoty SBS javu je vlnová dĺžka. Boli vykonané 4 scenáre, pri ktorých sa menila vlnová dĺžka a to o hodnotách 1260 nm (Obr. 8(a)), 1360 nm (Obr. 8(b)), 1460 nm (Obr. 8(c)) a 1625 nm (Obr. 8(d)). Jedná sa o hraničné vlnové dĺžky v pásmach O, E, S a L. Hraničná vlnová dĺžka pásma C bola vynechaná a to z dôvodu, že v predvolených parametroch je zvolená vlnová dĺžka z pásma C o hodnote 1550 nm.

Tab. 3 Prahové hodnoty a ich rozdiel oproti predvolenej hodnotev závislosti od vysielacej vlnovej dĺžky

Vysielacia vlnová dĺžka [nm]	Prahová hodnota [dBm]	Rozdiel oproti predvolenej hodnote [dBm]
1260	10.6	-2.2
1360	11.4	-1.4
1460	12	-0.8
1625	13	-0.2

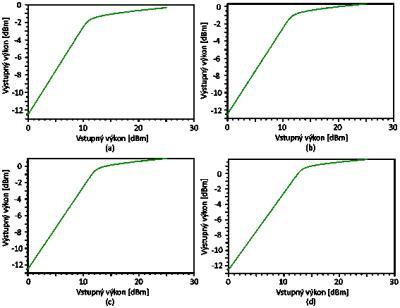
Obr. 8 Závislosť výstupného výkonu na vstupnom výkone pri vysielacej vlnovej dĺžke (a) 1260 nm, (b) 1360 nm, (c) 1460 nm a (d) 1625 nm

Zistené prahové hodnoty ako aj ich rozdiel oproti predvolenej hodnote pri daných vlnových dĺžkach sú uvedené v Tab. 3. Pri všetkých simuláciách bol nastavený rovnaký útlm vlákna (0.25 dB/km) a to z dôvodu aby bol zjavnejší rozdiel vplyvu SBS javu. Avšak prenos na menších vlnových dĺžkach je väčší útlm vo vlákne. Z Tab. 3 je vidieť, že pri menších vlnových dĺžkach je nižšia prahová hodnota SBS javu. Takže máme dva dôvody na prenos v optických vláknach pri vyšších vlnových dĺžkach a to SBS jav a útlm vlákna.

4. Záver

Prahová hodnota optického výkonu pre SBS jav je najnižšia z nelineárnych javov a pohybuje sa v rozmedzí jednotiek mW. Z toho dôvodu SBS jav patrí medzi jeden z najviac dominantných nelineárnych javov v optických komunikačných systémoch. Brillouinov rozptyl nastáva v spätnom smere, čiže vzniká nová vlna, ktorá smeruje k zdroju. Táto vlna je frekvenčne posunutá smerom nadol, frekvenčný posun spätne rozptýlenej vlny je približne o 11 GHz.

Najdôležitejším faktorom na limitovanie SBS javu je udržať vstupný výkon pod prahovou hodnotou. V takom prípade je dokonca možné zanedbať SBS jav v optickom komunikačnom systéme. Prahová hodnota SBS javu závisí od viacerých faktorov komunikačného systému, ale prevažne od optického vlákna. Na parametre optického vlákna, ktoré ovplyvňujú prahovú hodnotu SBS, bola práca zameraná a to konkrétne na zisk SBS, polarizáciu vlákna, priemer jadra vlákna a vlnovú dĺžku vstupného signálu. Najväčší vplyv na posun prahovej hodnoty SBS mal parameter zisk SBS. Použitím vlákna s nízkou hodnotou SBS zisku sa výrazne posunie prahová hodnota. To je potrebné práve pri prenose cez optické vlákno väčšej dĺžky, pretože sa dosiahne možnosť použitia väčších vstupných výkonov.

Použitie vyšších vlnových dĺžok v optických systémoch má teda dvojaký zmysel, jeden je vyššia prahová hodnota SBS a druhý je menší útlm optického vlákna na kilometer. Rovnako aj väčší priemer jadra vlákna zvyšuje prahovú hodnotu SBS. Samozrejme výber vlákien podľa priemeru jadra nie je veľký, a vysoký posun prahovej hodnoty na tomto parametre nezískame. Väčší posun prahovej hodnoty je možné získať polarizáciou vlákna, zároveň je potrebné dávať pozor na depolarizovanie vlákna, kedy sa znižuje prahová hodnota SBS javu.

Literatura

1. SINGH, S., P.; GANGWAR, R.; SINGH, N. : Nonlinear Scattering Effects in Optical Fibers. Progress In Electromagnetics Research, University of Allahabad, 2007.
2. RAMASWAMI, R.; SIVARAJAN, N. K.; SASAKI, H. G. : Optical Networks. USA, Elsevier Inc., 2010. 928 s. ISBN 978-0-12-374092-2.
3. AGRAWAL, P. G. : Nonlinear Fiber Optics. The Institute of Optics University of Rochester, New York, Academic Press is an imprint of Elsevier, 2013. 631 s. ISBN 978-0-12397-023-7.
4. FERREIRA, F. S. M. : Nonlinear Effects In Optical Fibers. John Wiley & Sons, Inc., Hoboken, New Jersey, 2011. 376 s. ISBN ISBN 978-0-470-46466-3.
5. LI, X.; GONG, H.; LI, S.; WANG J. : Experimental investigation on pulse light stimulated Brillouin scattering in the optical fiber. IEEE, 2011, iSBN: 978-0-8194-8961-6.
6. YENIAY A.; DELAVAUX, J.; TOULOUSE, J. : “Spontaneous and stimulated brillouin scattering gain spectra in optical fibers,” Lightwave Technology, Journal of, vol. 20, no. 8, Aug 2002, pp. 1425–1432.
7. M. Shaik, V. Achuth, D. Venkitesh, and B. Srinivasan, “Investigation of stimulated brillouin scattering spectra of an optical fiber with use of a frequency modulated laser,” in Communications and Photonics Conference and Exhibition, 2011. ACP. Asia, Nov 2011, pp. 1–6.

---

Spoluautormi článku sú Ing. Ľuboš Ovseník, PhD., Ing. Maroš Nosáľ, Katedra elektroniky a multimediálnych telekomunikácií, FEI TUKE, Slovenská republika