Obrazové textúry a ich popisovanie
14. Marec, 2016, Autor článku: Kováč Ondrej, Informačné technológie
Ročník 9, číslo 3  Pridať príspevok
Pridať príspevok
![]() Článok je orientovaný na úvod do problematiky obrazových textúr a možnostiam ich popisu. V článku sú popísané možné definície textúry ako takej. Základ príspevku tvoria definície metód popisu textúr a ich matematické vyjadrenie. Bližšie sú analyzované štatistické metódy. Medzi základné štatistické metódy patria metódy prvého rádu, ktoré sú ale málo účinné nakoľko nezohľadňujú kontext v ktorom sa obrazové prvky nachádzajú. Tiež sú analyzované štatistické metódy druhého rádu sú v tomto ohľade účinnejšie. V ďalšej časti je analyzovaná metóda založená na rozklade textúry do priestorovo-frekvenčnej oblasti diskrétnej waveletovej transformácie ktorá je tiež analyzovaná. V závere príspevku sú opísané dve databázy textúr na základe ktorých je možné vykonať analýzu textúr.
Článok je orientovaný na úvod do problematiky obrazových textúr a možnostiam ich popisu. V článku sú popísané možné definície textúry ako takej. Základ príspevku tvoria definície metód popisu textúr a ich matematické vyjadrenie. Bližšie sú analyzované štatistické metódy. Medzi základné štatistické metódy patria metódy prvého rádu, ktoré sú ale málo účinné nakoľko nezohľadňujú kontext v ktorom sa obrazové prvky nachádzajú. Tiež sú analyzované štatistické metódy druhého rádu sú v tomto ohľade účinnejšie. V ďalšej časti je analyzovaná metóda založená na rozklade textúry do priestorovo-frekvenčnej oblasti diskrétnej waveletovej transformácie ktorá je tiež analyzovaná. V závere príspevku sú opísané dve databázy textúr na základe ktorých je možné vykonať analýzu textúr.
Úvod
Analýza textúr má praktické využitie v mnohých smeroch a odvetviach. V meteorológii sa používa pri analýze a spracovaní družicových snímok, ďalej má využitie pri kontrole kvality rôznych výrobkov, ako je kvalita ovocia, papiera alebo technických súčiastok. Veľké uplatnenie má aj v medicíne pri analýze ultrazvukových a rtg. snímok, ale aj pri zisťovaní zrakových ochorení. Analýza v priestore DWT sa hodí hlavne na také účely, kde je potrebné porovnávať rôzne textúry s referenčnou textúrou. Takáto analýza je použiteľná napríklad pri kontrolovaní kvality výrobkov, kde vstupná textúra by bola bezchybný výrobok a od jej histogramu by sa počítali stredné kvadratické chyby histogramov textúr porovnávaných výrobkov. V prvej kapitole príspevku je definovaná textúra. Druhá kapitola popisuje základné metódy jej popisu textúr, bližšie je rozobratá problematika štatistických metód a metód založených na analýze textúr v priestorovo frekvenčnej oblasti. V ďalšej časti je popísaná diskrétna waveletova transformácia ako aj jej dvojrozmerná implementácia. V ďalšej kapitole sú uvedené a bližšie definované databázy, ktoré neskôr môžu byť použité pri klasifikácii textúr.
1. Definícia textúr
Textúry je subjektívne jednoduché rozoznať, ale ich jednotná definícia nie je. Existuje množstvo definícií zavedených v mnohých odborno-vedeckých publikáciách. Medzi najčastejšie uvádzané definície patria:
- Textúra je prirodzenou vlastnosťou každého povrchu akejkoľvek štruktúry- kôra stromov, štruktúra látky atď. Nesie dôležité informácie o usporiadaní štruktúry a vzťahu štruktúry k okolitému prostrediu. Aj keď je popis textúry a jej rozpoznanie voľným okom jednoznačné, nie je jednoduché textúru popísať jednotnou definíciou a analyzovať ju pomocou digitálnych techník [1].
- Obrazová textúra je definovaná počtom a typom svojich primitív a ich priestorovým usporiadaním. O akejkoľvek štruktúre, ktorá má hladký povrch môžeme z určitej vzdialenosti povedať, že nemá žiadnu textúru. So zväčšujúcim sa rozlíšením sa však textúra stane výraznejšou, od jemnejšej až po hrubú textúru pri vysokom rozlíšení [2].
- Oblasť v obraze má konštantnú textúru, ak je množina lokálnych štatistík alebo iných lokálnych vlastností obrazovej funkcie konštantná, pomaly sa meniaca, alebo aspoň približne periodická .
- Predstava textúry sa javí byť závislá na týchto 3 zložkách:
- Na určitom lokálnom usporiadaní, ktoré sa opakuje v danej oblasti, táto oblasť je väčšia v porovnaní s oblasťou usporiadania.
- Lokálne usporiadanie pozostáva z elementárnych častí, ktoré majú definované rozloženie.
- Elementárne časti sú približne rovnomerné entity, ktoré majú rovnaký rozmer všade, kde je oblasť danej textúry.
2. Metódy popisovania textúr
Zjednodušujúcim predpokladom viacerých algoritmov využívaných pri spracovaní obrazu je existencia oblastí v obraze, ktoré majú rovnomerné rozloženie intenzity jednotlivých obrazových prvkov (op). Reálne obrazy však také rovnomerné rozloženie intenzít nemajú. Je ale možné pri nich zaznamenať určité pravidelné zmeny intenzity op, ktoré tvoria určitý vzor a tento vzor sa nazýva textúrou. Metód pre popisovanie textúr je mnoho, všetky sú však založené na princípoch, ktoré sa delia do štyroch základných skupín. Ide o štatistické, geometrické, modelovo orientované, priestorovo-frekvenčne orientované metódy.
2.1. Štatistické metódy
Jednou z definičných vlastností textúry je priestorové rozloženie stupňov sivej v obraze. Použitie štatistických charakteristík danej textúry bolo jednou z prvých metód popisovaných v literatúre o počítačovom spracovaní obrazu. Štatistické metódy sa delia na štatistiky prvého rádu a štatistiky druhého rádu [1]. Štatistiky prvého rádu môžu byť získané z histogramu obrazu. Histogram je daný počtom op, ktoré majú určitú úroveň šedej (intenzitu). Pre 8-bitový obraz na x-ovej osi histogramu budú hodnoty z rozsahu <0, 255>, čo predstavuje všetky možné jasové úrovne obrazových prvkov obrazu. Na osi y bude počet výskytov op s danou hodnotou [3]. Na Obr. 1 je príklad histogramu s ôsmimi hodnotami intenzity.
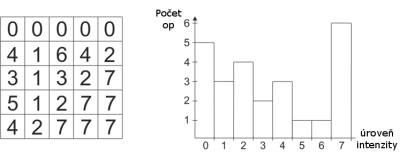
Obr. 1 Trojbitový obraz s rastrom 5×5 op a jemu prislúchajúci histogram
Medzi štatistiky prvého rádu patria stredná hodnota – mean (1), disperzia – variance (2), asymetria – skewness (3) a selektívnosť – kurtosis (4).
| (1) |
| (2) |
| (3) |
| (4) |
kde N je počet všetkých obrazových prvkov obrazu. Nevýhodou štatistík prvého rádu je, že neobsahujú žiadnu informáciu o vzťahu jednotlivých op voči okoliu. Túto skutočnosť ilustruje Obr. 2, kde je vidieť, že všetky matice majú rovnakú strednú hodnotu μ=0,5 a pritom nie sú identické [4]. Dá sa ukázať, že pre uvedené obrazy sú aj ostatné štatistiky rovnaké.
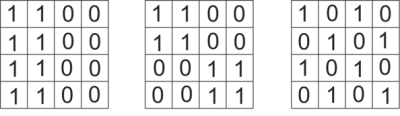
Obr. 2 Tri binárne obrazy s identickou strednou hodnotou
Štatistiky druhého rádu [5] sú založené na maticiach vzájomného výskytu. Sú to vlastne pravdepodobnosti výskytu dvoch op p1 a p2 s hodnotou jasu i a j, ktoré sú vo vzdialenosti d, teda na relatívnej pozícii δx, δy a majú rovnakú úroveň intenzity. Tento vzťah môže byť popísaný pravdepodobnostnou funkciou (5).
| (5) |
Podľa [4] môžu byť textúry vo väčšine prípadov popísane δx= δy=1 a v takomto prípade sa matica vzájomných výskytov počíta v štyroch základných smeroch
| (6) |
Ako základné štatistiky druhého rádu možno uviesť pravdepodobnosť rozdielnosti prvkov (7), entropiu (8) a energiu (9) ako indikátor rovnomernosti (uniformity).
| (7) |
| (8) |
| (9) |
Dá sa ukázať, že štatistiky pre obrazy na Obr. 2 budú pre každý obraz iné. Z uvedeného je zrejmé, že štatistiky druhého rádu sú pre popisovanie textúr vhodnejšie ako štatistiky prvého rádu.
2.2. Geometrické metódy
Geometrické metódy tiež známe ako štrukturálne metódy reprezentujú štruktúru s použitím presne definovaných primitív [2]. Keď sú tieto primitíva v textúre rozpoznané, používajú sa následne dve hlavné prístupy analýzy takýchto textúr. Prvý prístup spočíva vo výpočte štatistických vlastnosti elementov textúr a tie sa prezentujú ako črty textúry. Druhý prístup je založený na určení istého pravidla usporiadania elementov. Tento druhý prístup zahŕňa geometrické alebo syntaktické metódy analýzy textúry. Najznámejšie metódy sú: parametre Voronoiho mozaiky a štrukturálne metódy [5]. Tieto metódy sa používajú skôr pre syntézu obrazu, ako pre jeho analýzu.
2.3. Modelovo orientované metódy
V prípade modelovo orientovaných metód je textúra reprezentovaná použitím dômyselných matematických modelov. Parametre modelu zachytávajú nevyhnutné vnímané kvality textúr. Tieto metódy sú založené na nájdení takého matematického procesu (modelu), ktorý by mohol vytvoriť pozorované usporiadanie jednotlivých intenzít. Funkcia intenzity je kombináciou funkcie reprezentujúcej známu štrukturálnu informáciu na povrchu obrázka a aditívneho náhodného šumu. Reprezentatívne metódy tejto skupiny sú: modely náhodných polí (Markove náhodné polia, Gibbsove náhodne polia) a fraktály [6]. Tieto metódy sa taktiež používajú na syntézu textúr [7].
2.4. Metódy analýzy v priestorovo-frekvenčnej oblasti
Táto skupina metód je založená na Fourierovej, Gaborovej alebo Waveletovej transformácii [8]. Najviac používaná v týchto metódach je diskrétna waveletová transformácia (DWT). Analýza pomocou DWT patrí medzi metódy analýzy založené na transformácii obrazu do priestorovo-frekvenčnej oblasti. DWT je lineárna transformácia transformujúca dáta, ktorých dĺžka je celistvým násobkom hodnoty 2, na číselne rozdielny vektor rovnakej dĺžky. Je to nástroj, ktorý rozdeľuje dáta do rôznych frekvenčných zložiek a následne študuje každú zložku s rozdielnym rozlíšením. DWT je realizovaná kaskádou filtrov, po ktorých nasleduje decimácia na polovičnú hodnotu dátového vektora [9, 10]. Tento proces je reprezentovaný rozkladovým stupňom jednorozmernej (1R) DWT na obrázku Obr. 3
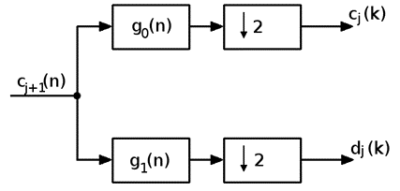
Obr. 3 Rozkladový stupeň 1R DWT
Ako je z Obr. 3 zrejmé, dekompozíciou vstupnej postupnosti sú získané dve postupnosti. Postupnosť cj(k) predstavuje aproximačnú časť a taktiež je vstupom do ďalšieho stupňa dekompozície, ktorý vo všeobecnosti môže byť rovnaký ako rozkladový stupeň na Obr. 3. Postupnosť dj(k) predstavuje detaily vstupnej postupnosti. Tento proces rozkladu je možné popísať pomocou (10) a (11).
| (10) |
| (11) |
kde g0(n) a g1(n) sú impulzné charakteristiky filtrov, operácia * predstavuje konvolúciu a operácia |2k reprezentuje decimáciu faktorom 2. Keďže textúry sú obrazy a tie považujeme za dvojrozmerné signály je potrebné 1RDWT upraviť. DWT sa radí medzi transformácie so separovateľným jadrom a preto je možné vykonať 1R DWT najprv na riadky a výsledok tejto transformácie potom ďalej podrobiť rozkladu 1R DWT po stĺpcoch. Týmto spôsobom je získaná 2R DWT dekompozícia. Tento postup je znázornený na Obr. 4 a zapojenie procesora 2R DWT je na Obr. 5.

Obr. 4 Postupný rozklad obrazu pomocou 1RDWT
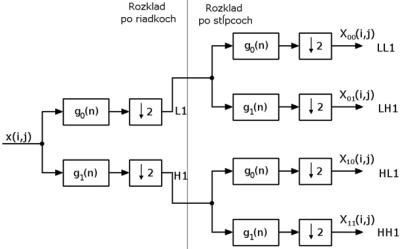
Obr. 5 Zapojenie procesora 2R DWT
Jednotlivé subobrazy sú následne analyzované. Rozšírením a prahovaním sú vytvorené výsledné frekvenčné modely, ktoré slúžia ako klasifikátory textúr.
3. Databázy obrazových textúr
Za účelom výskumu popisovania textúr je potrebné rozlišovať dve databázy. Prvá predstavuje štandardnú databázu (ŠD) a druhá mernú databázu (MD). V nasledujúcich podkapitolách budú uvedené príklady takýchto možných databáz.
3.1. Štandardná databáza
Pre potreby porovnávania účinnosti jednotlivých analyzátorov bolo potrebné zostaviť databázu rôznych obrazových textúr. Štandardnú databázu je možné zostaviť napr. z 56 obrazových textúr v odtieni šedej, ktoré sú vo formáte BMP a majú rozmer 512×512 op. Takto vytvorená štandardná databáza je zobrazená na Obr. 6, ktorá bola zostavená výberom 54 textúr z tzv. „Brodatz“ textúr. Ich názov vznikol po mene autora P. Brodatz, ktorý ich uverejnil vo svojej knihe „Textures: a photographic album for artists and designers“ [11]. V tejto štandardnej databáze sa nachádzajú aj 2 textúry, ktoré nie sú od tohto autora, figurujú pod označením T_1 a T_2. Označenia od 1.1.01 po 1.1.12 patria základným „Brodatz“ textúram a zachytávajú rôzne štruktúry, ako kôra stromov, tehly, slama atď. Pod názvami 1.2.01 až 1.2.12 sa nachádzajú histogramovo vyhladené verzie textúr 1.1.01 až 1.1.12 a pod označeniami 1.3.01-1.3.12 sa vyskytujú tie isté obrazové textúry ako pri predošlých označeniach, avšak v iných mierkach. 1.4.01 – 1.4.18 označujú rôzne iné obrazové textúry.
3.2. Merná databáza
Za účelom výskumu v oblasti popisovania textúr je potrebné tiež zostaviť mernú databázu možných obrazových textúr. V tejto databáze sa vo všeobecnosti nachádzajú rôzne druhy obrazových textúr v odtieňoch šedej alebo farebné, pričom tieto môžu sa v nej vyskytovať v niekoľkých formách. Príklad štruktúry tejto mernej databázy v ktorej jednotlivé druhy obrazových textúr predpokladajú výskyt ich 20 foriem je ilustrovaný na Obr.7.
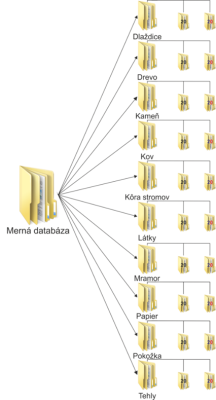
Obr. 7 Štruktúra mernej databázy.
Záver
V článku bol uvedený prehľad možných prístupov k definícii textúr. Taktiež boli analyzované možné metódy popisu textúry. Boli analyzované štatistické metódy, ktoré je možné rozdeliť do dvoch skupín. Prvá skupina pozostáva z metód štatistickej analýzy prvého rádu. Tu sa radi stredná hodnota, disperzia, šikmosť a ostrosť. Nedostatkom týchto metód je, že nezohľadňujú polohu obrazového prvku vzhľadom na ostatné prvky. Tieto nedostatky odstraňujú štatistické metódy druhého rádu. Medzi tieto metódy sa radi rozdielnosť, entropia a energia. Ďalšie metódy sú založené na analýze textúr v priestore spektrálnych alebo rozkladových koeficientov. V článku bola analyzovaná DWT ktorá sa v nedávanej minulosti stala v oblasti analýzy a syntézy obrazov a textúr veľmi populárnou. V poslednej časti príspevku sú uvedené dva možné spôsoby zostavenia databáz s pomocou ktorých na základe popisov textúr môžu byť tieto textúry klasifikované.
Literatúra
- R. M. Haralick, K. Shnmugam a I. Dinstein, „Textural features for image classification,“ IEEE Transactions on system, Man and Cybernetics, zv. 3, 1973.
- M. Tuceryan a A. K. Jain, „ Texture analysis in Handbook of Pattern Recognition and Computer Vision,“ Singapore: World Scientific, 1993.
- G. Gimel, „Texture analysis and its applications.,“ 2006. [Online]. Available: http://www.cs.auckland.ac.nz/~georgy/research/texture/thesis-html/node7.html. [Cit. 22 2 2016].
- H. Siegl, Quantification of Posterior Capsule Opacification after Cataract Surgery, PhD Thesis. University of Vienna, 2000.
- J. S. Weszka, „A comparative study of texture measures for terrain classification,“ SMC, zv. 6, %1. vyd.4, 1976.
- B. Mandelbrot, The Fractal Geometry of Nature., San Francisco, 1982.
- G. Gimel’farb, L. Van Gool a A. Zalesny, „To frame or not to frame in probabilistic texture modelling?,“ rev. 17th International Conference on Pattern Recognition (ICPR’04), 2004.
- J. Mihalík a J. Zavacký, Diskrétne spracovanie signálov, Košice: LČSOV FEI TU, 2011.
- J. Mihalík a O. Kováč, Číslicové spracovanie textúr ľudskej hlavy, Košice: TU, 2014.
- S. Arivazhagan a L. Ganesan, „Texture classification using wavelet transform,“ Pattern Recognition Letters, 2003.
- P. Borodatz, Textures: a photographic album for artists and designers, 1966.
Spoluautormi článku sú Ján Mihalík a Patrik Čajko, Laboratórium číslicového spracovania obrazov a videokomunikácií, Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach.


