V technologických procesoch hutníckych a strojárenských závodov je ohrev kovov jednou z najdôležitejších operácií majúci vplyv na výrobu po stránke výkonnosti, akosti a nákladov. Teplota vsádzky je rozhodujúcou veličinou v procesoch ohrevu, pretože umožňuje určiť fázu spracovania vsádzky, čas kedy dôjde k požadovanej zmene štruktúry spracovávaného materiálu. V súčasnosti sa v technologických procesoch teplota vsádzky nemeria z nasledovných dôvodov: konštrukčné prevedenie pece (pohybujúca sa vsádzka), deštrukcia meracieho snímača pri jeho montáži alebo v priebehu procesu, zvýšené náklady na prevádzku pece atď. V článku je popísaný matematický model založený na metóde konečných rozdielov pre modelovanie vnútorných teplôt vo vsádzke, ktorým je oceliarenský zvitok žíhaný v poklopovej peci. Model vypočíta vnútornú teplotu vsádzky na základe meranej teploty na jej povrchu v priebehu procesu žíhania. Presnosť modelu bola vyhodnotená s využitím experimentálnych meraní na reálnej poklopovej peci a vytvoreného simulačného modelu v programovom prostriedku MATLAB.

Úvod

Proces žíhania je jednou z dôležitých operácií pri výrobe oceľových plechov valcovaných za studena, ktorý významne ovplyvňuje kvalitu finálnych výrobkov. V tomto procese sa zvitky valcované za studena pomaly zohrejú na požadovanú teplotu (fáza ohrevu), na ktorej sa držia predpísaný čas (fáza výdrže). Po fáze výdrže sa zvitky pomaly ochladia na výstupnú teplotu (fáza ochladzovania). Stanovenie adekvátneho režimu ohrevu kovov predstavuje problém s ktorým sa stretávame aj pri žíhaní oceliarenských zvitkov. Operátor žíhania nemôže jednoducho ohriať zvitky a následne ich ochladiť, ale musí zabezpečiť ohrev, udržiavanie teploty a ochladzovanie podľa diagramu tepelného spracovania. Tento proces by nebol čo najefektívnejší bez definovanej teploty ochrannej atmosféry a vnútornej teploty žíhaného zvitku. Modelovanie žíhacieho procesu je veľmi sofistikovaná a nákladná práca, ktorá však môže priniesť informácie umožňujúce predpoveď času vykurovania, chladenia a predikciu trendov vnútorných teplôt žíhaného zvitku. Modelovanie tohto procesu sa môže uskutočniť s využitím modelov nepriameho merania teplôt (napríklad vo forme dvojrozmerných teplotných tabuliek a grafov).

Pre nepriame meranie teploty sú vo svete vyvíjané rozličné metódy. Napríklad v článku [1] autori vyvinuli a overili matematický model na meranie povrchovej teploty objektu termovíznou kamerou. Tento matematický model bol použitý na kvantifikáciu chyby merania teploty pri dvojfarebnej technike. Bola poskytnutá nová korelácia na odhad chyby merania teploty. V tomto článku je popísaný matematický model, ktorý umožňuje nepriamo merať (vypočítať) vnútorné teploty žíhaného zvitku z jeho priamo meraných povrchových teplôt. Matematický model je vytvorený s využitím metódy konečných rozdielov upravenej pre dvojrozmerný cylindrický súradnicový systém. Matematický model je verifikovaný pomocou dát získaných z experimentálnych meraní na reálnej poklopovej peci a s využitím simulačného modelu vytvoreného v programovom prostriedku MATLAB.

Proces žíhania

Tepelné spracovanie pozostáva z ohrevu kovu alebo zliatiny na určitú požadovanú teplotu, udržiavanie pri tejto teplote a následné ochladenie, ktoré určuje mnohé mechanické vlastnosti ocelí. Výsledkom tohto procesu sú zmeny vlastností a štruktúry kovov. Na Obr. 1a je znázornená schéma diagramu tepelného spracovania.

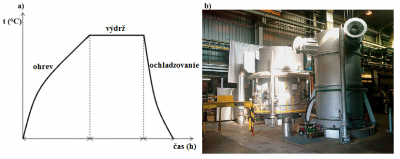
Obr. 1 a) Diagram tepelného spracovania b) Poklopová pec

Rekryštalizačné žíhanie sa prevádza u ocelí tvárnených za studena ich ohrevom na rekryštalizač¬nú teplotu (obvykle na teploty v rozmedzí 550 – 700 °C), zotrvaním na tejto teplote zhruba 1 hod. a následným ochladzovaním ľubovoľnou rýchlosťou. Oxidácia (hrdza) sa môže vyskytnúť, ak je povrch horúcej ocele vystavený pôsobeniu vzduchu. Preto, aby sa zabránilo oxidácii počas ohrievania ocele a aby sa umožnilo jej chladenie, sa takáto oceľ drží v uzatvorenom prostredí v ochrannej atmosfére. Žíhanie sa robí obyčajne v 3 krokoch [2] [3]:

• Ohrev – vsádzka sa najprv zahreje na predpísanú teplotu.
• Výdrž – vsádzka sa na predpísanej teplote udrží predpísaný čas (izotermické spracovanie), aby sa rovnomerné zohriala v celom svojom objeme.
• Ochladzovanie – vsádzka sa nechá vychladnúť.

Niekedy je žíhanie tvorené aj viac ako 3 krokmi. Takýto postup sa nazýva žíhací program. Zahrievanie/ochladzovanie sa robí buď horúcim vzduchom alebo v soľnom kúpeli. Teplota žíhania je často blízka teplote začiatku tavenia materiálu, nikdy ju však nesmie prekročiť. Cieľom žíhania je najčastejšie zvýšenie húževnatosti, ťažnosti a medze pevnosti. Žíhanie sa veľmi často používa v spojení s oceľou a liatinou, je ho však možné využiť aj pre iné zliatiny [3]. Poklopové pece sa používajú na žíhanie oceľových zvitkov a pozostávajú z týchto základných častí:

• Podstavec pre ukladanie oceľových zvitkov v poklopovej peci.
• Vnútorný ochranný poklop zo žiaruvzdorného plechu.
• Žíhací poklop, ktorý je z vnútra pokrytý žiaruvzdornou výmurovkou. Jeho tvar je prispôsobený vsádzke (používajú sa štvorcové alebo tiež aj kruhové poklopy rozličných veľkostí).

Poklopové pece sa ohrievajú plynným palivom, najčastejšie pomocou sálavých trubiek alebo elektriky. Každý žíhací poklop má tri podstavce. Na jednom prebieha proces žíhania, na druhom proces ochladzovania a na treťom príprava novej vsádzky. Zvýšenie produktivity poklopových pecí umožňujú špeciálne chladiace poklopy, ktoré sa na ochranný poklop nasádzajú po skončenom ohreve a vyrovnávaní teploty [4]. Poklopovú pec na žíhanie zvitkov môžeme vidieť na Fig. 1b. Pri žíhaní sa používa plyn HNX. Je to pomer vodíka a dusíka v ochrannej atmosfére:

• Vodík v rozmedzí od 3% do 30%.
• Dusík v rozmedzí od 70% do 97%.

Matematický model pre nepriame meranie vnútornej teploty

Pri vytváraní matematických modelov tepelných agregátov je dôležité zvládnuť riešenie procesu vedenia tepla. Tento proces je charakterizovaný ako proces prenosu tepelnej energie pri kontakte rôznych častí objektov alebo jednotlivých objektov, ktoré majú rozdielne teploty. Riešenie teplotného poľa skúmaného objektu potom vychádza z Fourierovej parciálnej diferenciálnej rovnice vedenia tepla, ktorá pre cylindrické súradnice zobrazené na Obr. 2 má nasledovný tvar [5]:

(1)

kde T – teplota (K), a – koeficient teplotnej vodivosti (m².s^-1), r, φ, z – súradnice v priestore (m), τ – čas (s). Koeficient teplotnej vodivosti vypočítame podľa rovnice

(2)

kde λ – koeficient tepelnej vodivosti (W.m^-1.K^-1), ρ – hustota (kg.m^-3) , c – koeficient mernej tepelnej kapacity (J.kg^-1.K^-1).

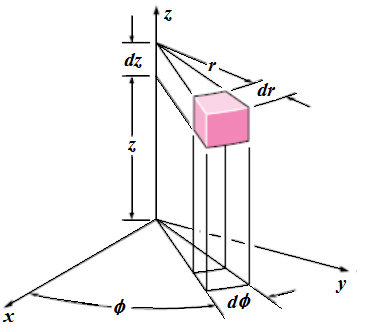
Obr. 2 Cylindrický súradnicový systém

Model prenosu tepla v cylindrických súradniciach pre trojrozmerné teleso môžeme v našom prípade zjednodušiť pre model dvojrozmerného telesa, pretože ohrev oceliarenského zvitku je po obvode rovnaký:

(3)

Pre tvorbu matematického modelu procesu žíhania je potrebné určiť závislosti teplo-fyzikálnych parametrov ako je tepelná vodivosť, merná tepelná kapacita a hustota. Veľmi dôležité je určiť tepelnú vodivosť pre anizotropné materiály (vsádzku), ktorej typickým predstaviteľom je žíhací zvitok [6].

Teplo je prenášané z povrchu zvitku hlavne prostredníctvom vedenia do vnútra, ale v dôsledku prítomnosti medzier medzi vinutiami zvitku, nie je jednoduchý model vedenia adekvátny pre popísanie ohrevu vo vnútri zvitku. Z toho dôvodu sa používa účinná tepelná radiálna vodivosť za účelom modelovania rozdelenia tepla vo vnútri zvitku. V ideálnom zvitku je teplo prenášané v radiálnom smere cez striedajúce sa vrstvy ocele a žíhacieho plynu. V reálnom zvitku sú ešte aj iné faktory, ktoré ovplyvňujú účinné radiálne vedenie. Niektoré z nich sú nasledovné:

• Premenlivá drsnosť povrchu plechov.
• Tepelná radiácia pridávajúca iný faktor k radiálnemu prenosu tepla vo zvitku.

Vo všeobecnosti je celková radiálna vodivosť súborom funkcií závislých na mnohých parametroch ako sú napríklad merné teplo, tepelná vodivosť, hustota, teplotný vzostup a pevnosť zvitku, rovnako ako vlastnosti výplňového plynu (tepelná vodivosť a hustota). V riešenom modely môže byť účinná tepelná radiálna vodivosť definovaná v podmienkach vodivosti oceľového zvitku a výplňového plynu a ich relatívneho pomeru použitím nasledujúcej rovnice [7]:

(4)

kde λ_r – tepelná vodivosť vrstvy ocele a plynu (W.m^-1.K^-1), λ_o – tepelná vodivosť ocele (W.m^-1.K^-1), λ_p – tepelná vodivosť výplňového plynu (W.m^-1.K^-1), d_s – priemerná hrúbka plechu zvitku (m), d_g – priemerná hrúbka medzery medzi vinutiami zvitku (m) .

V riešenom modeli sa v smere osi z použila hodnota tepelnej vodivosti na základe chemického zloženia ocele žíhaného zvitku.
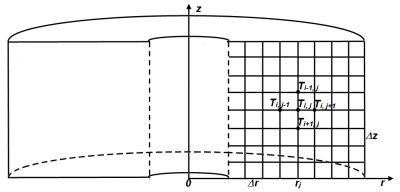
Pre riešenie diferenciálnej rovnice (3) je použitá metóda konečných rozdielov [8]. Na skúmanom objekte, ktorým je oceliarenský zvitok je vytvorená sieť (Obr. 3), ktorá vznikne vedením rovnobežiek so súradnicovými osami vo vzdialenosti ∆r v smere osi r a vo vzdialenosti ∆z v smere osi z. Teplota je definovaná v jednotlivých uzlových bodoch súradnicového systému, kde i je index bodu v smere osi z, j je index bodu v smere osi r a k je časový krok. Tak T_i,j,k je teplota v uzlovom bode, ktorý leží na priesečníku i-tej rovnobežky s z-tovou súradnicou a j-tej rovnobežky s r-tou súradnicou v čase τ=k∙∆τ.

Obr. 3 Sieť v reze zvitku

Ak v rovnici (3) nahradíme derivácie diferenciami tak získame rovnicu

(5)

kde – je pozícia v smere osi r umiestnená v strede medzi uzlami s teplotou T_i,j+1,k a T_i,j,k (m) – je pozícia v smere osi r umiestnená v strede medzi uzlami s teplotou T_i,j-1,k a T_i,j,k (m), a_r1 a a_r2 – koeficienty teplotnej vodivosti v smere osi r, a_z1 a a_z2 – koeficienty teplotnej vodivosti v smere osi z. Teplotu v nasledovnom časovom kroku T_i,j,k+1 môžeme potom určiť nasledovne

(6)

kde koeficienty teplotnej vodivosti sú uvažované ako funkcie teploty v nasledovnom tvare

(7)

Časový krok riešenia je vypočítaný podľa

(8)

Experimentálne merania

Pri experimentálnych meraniach boli zohľadnené rôzne žíhacie režimy, priemery a hmotnosti zvitkov. Previedli sa 4 experimentálne merania, ktoré sa líšili množstvom (počet žíhaných zvitkov), rozmerom (priemer zvitku), hrúbkou plechu vsádzky a žíhacím režimom. Priemery a hrúbky plechov žíhaných zvitkov pre jednotlivé merania sú uvedené v Tab. 1. Na Obr. 4 sú vyznačené miesta umiestnenia termočlánkov vo zvitkoch pri realizovaných experimentálnych meraniach (žíhacích režimoch). Povrchové teploty T₁, T₂, T₃, T₄, T₅, T₉, T₁₀, T₁₁, T₁₂, T₁₃ budú vstupom do matematického modelu v zodpovedajúcich povrchových uzlových bodoch zvolenej dvojrozmernej siete (Obr. 3). Teploty v povrchových uzloch siete, kde neboli umiestnené termočlánky budú získané pomocou lineárnej aproximácie medzi dvoma najbližšími povrchovými uzlami s priamo meranými teplotami. Vnútorné teploty T₆, T₇, T₈ budú slúžiť pre porovnanie priebehu priamo meraných a vypočítaných vnútorných teplôt.

Tab. 1 Priemery a hrúbky zvitkov

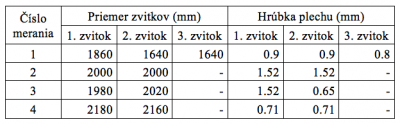
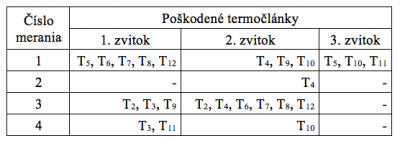
Spoľahlivosť termočlánkov po meraní bola posudzovaná vizuálne (mechanické poškodenie – rozseknutý termočlánok) a kontrolným meraním statickej charakteristiky snímača (termočlánku). Po tejto analýze boli pre verifikáciu matematického modelu vylúčené chybné termočlánky. V Tab. 2 sú uvedené poškodené termočlánky v konkrétnych zvitkoch pre jednotlivé merania.

Tab. 2 Poškodené termočlánky

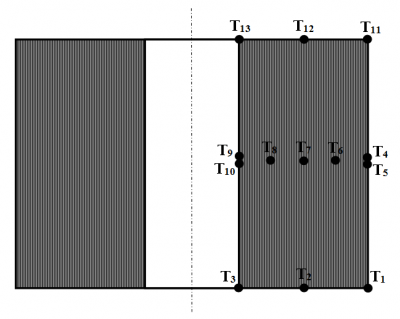
Obr. 4 Meracie miesta v reze zvitku

Priebeh priamo meraných teplôt zo zvitku 2 pri druhom experimentálnom meraní je zobrazený na Obr. 5. Pri tomto meraní došlo k poškodeniu termočlánku, ktorý meral teplotu T₄. Z tohto dôvodu nie je teplota T₄ viditeľná pri priebehu teplôt T₁,T₄,T₅,T₁ na Obr. 5. Jej namerané hodnoty boli mimo merací rozsah termočlánku.

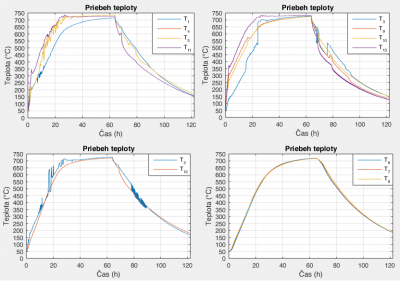
Obr. 5 Priebeh priamo meraných teplôt vo zvitku 2 pri druhom experimentálnom meraní

Verifikácia matematického modelu

Za účelom verifikácie navrhnutého matematického modelu bol zostavený simulačný model v programovom prostriedku MATLAB. Simulačný model umožňuje vypočítať vnútorné teploty žíhaného zvitku na základe jeho priamo meraných povrchových teplôt, ktoré sa načítajú zo súboru. Vypočítané teploty sú zobrazené v reze zvitku s využitím dvojrozmerného poľa a farebnej škály Jet. Príklad zobrazenia vypočítaných teplôt pre vybrané časové okamihy experimentálneho merania 2 zo zvitku 2 je uvedený na Obr. 6. Simulačný model umožňuje aj vykresliť grafy, ktoré porovnávajú priamo merané a vypočítané vnútorné teploty T₆, T₇ a T₈. Porovnania vnútorných teplôt pre jednotlivé zvitky sú uvedené na Obr. 7, 8 a 9. Pre 1. zvitok v experimentálnom meraní 1 a 2. zvitok v experimentálnom meraní 3 nebol vykonaný výpočet z dôvodu poškodenia termočlánkov pre meranie vnútorných teplôt T₆, T₇ a T₈.

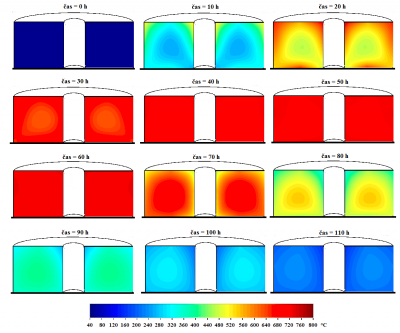
Obr. 6 Rez zvitku 2 v experimentálnom meraní 2

Výsledok verifikácie matematického modelu je prezentovaný výpočtom vo forme relatívnej odchýlky teploty pre vybrané meranie a zvitok

(9)

kde δT – relatívna odchýlka pre zvolenú teplotu (%), T_i^mod – teplota vypočítaná matematickým modelom v i-tom časovom kroku (°C), T_i^mer – teplota priamo meraná v i-tom časovom kroku (°C), n – celkový počet časových krokov v rámci merania (žíhacieho cyklu).

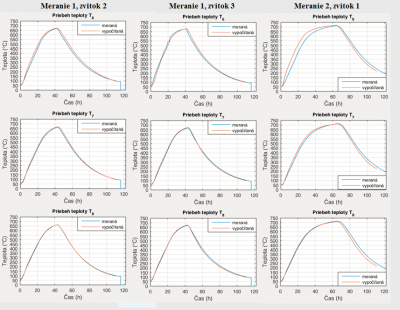
Obr. 7 Porovnanie teplôt pri experimentálnom meraní 1 (zvitok 2 a 3) a meraní 2 (zvitok 1)

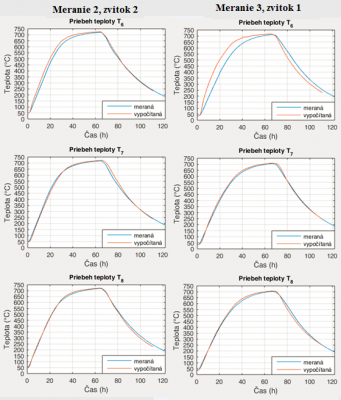
Obr. 8 Porovnanie teplôt pri experimentálnom meraní 2 (zvitok 2) a meraní 3 (zvitok 1)

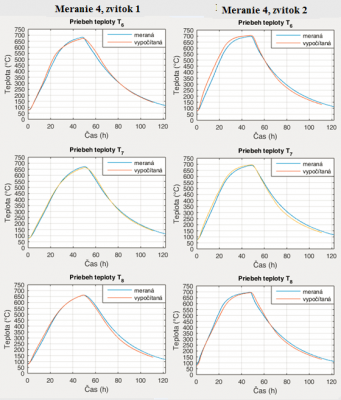
Obr. 9 Porovnanie teplôt pri experimentálnom meraní 4 (zvitok 1 a 2)

Hodnoty relatívnej odchýlky vnútorných teplôt T₆, T₇ a T₈ pre vybrané meranie a zvitok sú uvedené v Tab. 3. Výsledná vypočítaná priemerná hodnota relatívnej odchýlky pre teplotu T6 je 7.29 %, pre T₇ je 3.25 % a pre T₈ je 3.63 %. Priemerná hodnota relatívnej odchýlky pre zvolenú teplotu bola vypočítaná ako suma relatívnych odchýlok tejto teploty cez všetky experimentálne merania a zvitky, ktorá následne bola podelená počtom týchto relatívnych odchýlok.

Tab. 3 Relatívna odchýlka pre vnútorné teploty vo zvitkoch pri realizovaných experimentálnych meraniach

Záver

V článku je popísaný matematický model pre nepriame meranie (výpočet) vnútorných teplôt oceliarenského zvitku žíhanom v poklopovej peci. Pre zostavenie matematického modelu je použitá metóda konečných diferencií upravená pre cylindricky súradnicový systém. Vstupom do matematického modelu sú priamo merané povrchové teploty vo zvolených uzlových bodoch siete a výstupom sú vypočítané vnútorné teploty. Navrhnutý matematický model bol overený s využitím štyroch experimentálnych meraní a programového prostriedku MATLAB.
Z uvedených priebehov v kapitole verifikácia matematického modelu na Obr. 7, 8 a 9 je vidieť kvalitatívnu zhodu s malými odchýlkami medzi priamo a nepriamo meranou teplotou T₇ a T₈. Pri teplote T₆ sú viditeľné väčšie rozdiely. Túto skutočnosť potvrdzuje aj veľkosť relatívnej odchýlky pre vnútorné teploty uvedená v tab. 3 a hodnota priemernej relatívnej odchýlky teploty T₆ 7.29 %.

V procese žíhania je dôležité, aby sa v celom objeme žíhaného zvitku dosiahla rekryštalizačná teplota, ktorá rozhodujúcou pre zmenu vlastností a štruktúry žíhanej ocele. To znamená, že aj najchladnejšie miesto vo zvitku musí dosiahnuť túto teplotu. Z Obr. 6 vyplýva, že najchladnejšie miesto vo zvitku sa nachádza v oblasti merania teplôt T₇ a T₈, ktorých priemerná relatívna odchýlka je 3.25 % pre teplotu T₇ a 3.63 % pre teplotu T₈. Môžeme konštatovať, že tieto hodnoty spĺňajúcou požiadavky reálnej prevádzky na kvalitu informácie o vnútorných teplotách žíhaného zvitku. Riadenie procesu žíhania na základe vnútornej teploty sa javí ako vhodný spôsob pre dosiahnutie rekryštalizačnej teploty v celom objeme zvitku a s možným znížením doby výdrže pri žíhaní, ktorá je v súčasnosti stanovená experimentálne. Zníženie doby výdrže by prinieslo ušetrenie finančných nákladov na prevádzku pece a informácia o vnútorných teplotách zvýšenie kvality žíhanej vsádzky dodržaním stanovených diagramov tepelného spracovania pre vybranú vsádzku.

Poďakovanie

Tento príspevok vznikol za podpory projektov APVV-14-0892, VEGA 1/0273/17, VEGA 1/0529/15 a Slovenskej spoločnosti aplikovanej kybernetiky a informatiky (SSAKI), ktorá je členom Zväzu Slovenských vedeckotechnických spoločností (ZSVTS).

Literatúra

1. Musto M., Rotondo G., Cesare M. D., Vecchio A. D., Savino L., Filippis F. D., Error analysis on measurement temperature by means dual-color thermography technique, Measurement 90 (2016) 265277.
2. Kremer R., Obroučka K., Ohřev kovů. SNTL, PRAHA, 1974. ISBN 04-401-74
3. Verhoeven, J. D.: Fundamentals of Physical Metallurgy, Wiley, New York, 1975, p. 592, ISBN 978-0-471-90616-2
4. Tatič, M., Lukáč, L, Priemyselné pece. ISBN 978-80-553-0254-6
5. Latif M. Jiji, Heat Conduction, Springer, Košice, 2009. 431 s. ISBN 978-3-642-01266-2
6. Hašek, P., Tabulky pro tepelnou techniku, VŠB, 247 s., Ostrava, 1988
7. Lisogor, A. A., Mitkalinnyi, V. I., Tepelné a fyzikálne vlastnosti nastohovanej ocele valcovanej za studena, (Heat and physical properties of cold rolling steel). 995-998, December
8. Kostúr, K., Simulačné modely tepelných agregátov, Vydavateľstvo Štroffek, Košice, 1997. 170 s. ISBN 80-967325-2-8