Analýza vlastností akčných členov pre jednosmerné motory

28. September, 2009, Autor článku: Tesár Richard, Elektrotechnika, Strojárstvo
Ročník 2, číslo 9 Pridať príspevok

motorcek Jednosmerný motor v pohonnej sústave je rotačný menič energie. Motor mení elektrickú energiu na mechanickú a generátor mechanickú energiu na elektrickú. Vo všeobecnosti v prevádzke ten istý stroj vykonáva obidve funkcie, a to podľa prevádzkových stavov sústavy. Funkcia jednosmerného motora vyplýva z fyzikálnych zákonitostí, ktoré možno vyjadriť matematickými opismi.

Zo základných zákonov sú to :

indukčný zákon
zákon o elektrodynamických silách v magnetickom poli

Zmena magnetického toku $\Phi$ viazaná s cievkou s N závitmi, vyvolá indukované napätie:

$u_i = N \frac{d \Phi}{d t}$

(1)

Vo všeobecnosti je teda magnetický tok funkciou času t a relatívnej polohy cievky k osi toku, vyjadrenej uhlom natočenia $\alpha$ . Potom základná všeobecná rovnica pre indukované napätie:

$u_i = \omega N \frac{d \Phi}{d \alpha} + N \frac{d \Phi}{d t}$

(2)

pričom

$\omega = \frac{\partial \alpha}{\partial t}$

(3)

a nech

$\Phi = \bar{B} * \bar{S} = B * S * \cos \alpha$

(4)

$u_i = N ( - B * S * \sin \alpha \frac{d \alpha}{d t})$

(5)

Vplyvom indukovaného napätia ui cievky preteká uzatvoreným obvodom prúd i. Týmto dvom veličinám zodpovedá v časovej jednotke elementárna energia :

$d W = u_i * i * dt$

(6)

a po úprave a dosadení vychádza všeobecná rovnica pre točivý moment pôsobiaci na cievku:

$M = i * N \frac{\partial \Phi}{\partial \alpha} + \frac{i}{\omega} * N \frac{\partial \Phi}{\partial t}$

(7)

Alebo pomocou Biot-Savartovho zákona a pravidla ľavej ruky vieme určiť smer pôsobenia sily F, ktorá je vyjadrená vzťahom:

$F = l * (B \times i) =l * B * I \sin \phi$

(8)

kde uhol $\phi$ je medzi vektorom magnetickej indukcie B a prúdom I.

Cievka v magnetickom poli pôsobením prúdu vytvára dvojicu síl F, ktorá vytvára elektromagnetický moment motora (obr.3)

$M_m = F * r = l * B * r * I * \sin \phi$

(9)

Rovnice (2) a (7) sú základné rovnice, všeobecne platné pre všetky druhy strojov. Tvar a znenie rovníc závisia od druhu konštrukcie stroja.

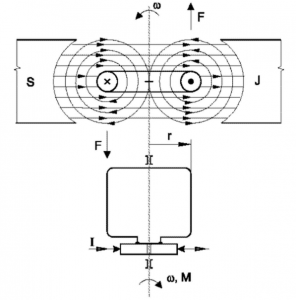
Obr. 3 Cievka v magnetickom poli, principiálna schéma jednosmerného motora

Konštrukčné usporiadanie jednosmerného motora je nasledovné:

stator – magnetický obvod z liatej ocele alebo plechov, má zabudované cievky budiaceho vinutia hlavných pólov (HP)
rotor – zväzok plechov vzájomne izolovaných, v drážkach je uložené vinutie kotvy
zberacie ústrojenstvo – systém uhlíkových kief

Druhy a vlastnosti jednosmerných motorov

Jednosmerné motory možno rozdeliť do rôznych skupín:

a) podľa stupňa riaditelnosti

jednorýchlostný, viacrýchlostný a s plynule nastaviteľnou rýchlosťou

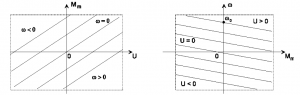
motor pre jeden zmysel otáčania – môže pracovať len v jednom kvadrante roviny $\omega$ , M; nieje určený pre elektrické brzdenie (obr. 4)

motor pre obidva zmysly otáčania – môže pracovať v I. alebo III. kvadrante roviny $\omega$ , M; tiež nieje určený pre elektrické brzdenie (obr. 4)

motory pre obidva zmysly momentu či sily pri rovnakom smere otáčok – môže pracovať v I. a II. kvadrante, alebo v III. a IV. kvadrante roviny $\omega$ ,M ; umožňujúci elektrické brzdenie (obr. 4)

reverzačné motory pre obidva zmysly smeru otáčania a momentu – umožňujúce reverzáciu pohonu počas behu; pracujú vo všetkých kvadrantoch roviny $\omega$ , M (obr. 4)

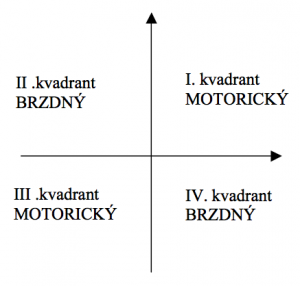
Obr. 4 Pracovné oblasti jednosmerného motora

b) Podľa zapojenia budiaceho vinutia:

jednosmerný motor s cudzím budením

jednosmerný motor s cudzím konštantným budením – s permanentnými magnetmi

sériový jednosmerný motor

derivačný motor

kompaudný motor

Jednosmerný motor s cudzím budením

Tento druh motora má oddelené statorové vinutie, ktoré je napájané z vlastného zdroja prúdu. Vlastné magnetické pole statora je potom celkom nezávislé na rýchlosti otáčania motora. Vplyvom chýbajúceho indukovaného napätia motora ( $\omega$ = 0), ktoré pôsobí proti svorkovému napätiu v okamihu pripojenia motora na sieť sa vyvolá veľmi veľký prúd kotvy. Aby sme zabránili škodám a poruchám treba voliť také možnosti spúšťania, ktoré vylučujú tieto možnosti. Preto treba:

obmedziť spúšťací prúd na prípustnú hodnotu
vytvoriť vhodný rozbehový moment pre pracovný mechanizmus

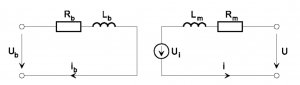
Obr. 5 Náhradná elektrická schéma JM s cudzím budením

Matematický model:

pre obvod budenia

$u_b = R_b i_b + L_b \frac{d i_b}{d t}$

(10)

pre obvod rotora

$u = R_m i + L_m \frac{d i}{d t} + u_i$

(11)

pre mechanický subsystém

$M_m - M_z = M_d = J_m \frac{d \omega _m}{d t}$

(12)

Uhlovú rýchlosť kotvy možno riadiť nasledovnými spôsobmi:

zmenou napätia kotvy

zmenou magnetického toku $\Phi$

zmenou odporu obvodu kotvy

riadenie impulzným napätím

Jednosmerný motor s permanentnými magnetmi

V tomto motore sa používajú na vytvorenie magnetického poľa permanentné magnety, a tým odpadá vinutie statora. Keďže tento typ motora je v praxi najpoužívanejší, má najlepšie regulačné vlastnosti, budeme sa s ním zaoberať trochu podrobnejšie.

Dynamický model JM s cudzím konštantným budením:

$u = R_m i + L_m \frac{d i}{d t} + u_i$

(13)

$u_i = C_u \omega$

(14)

pre mechanický subsystém

$M_m = M_z = M_d = J_m \frac{d \omega_m}{d t}$

(15)

$M_m = C_u * i$

(16)

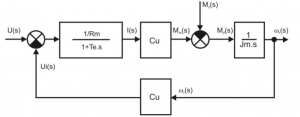
Obr. 6 Dynamický model JM s cudzím konštantným budením

Opis v stavovom priestore:

$\frac{d}{d t} \begin{bmatrix} {i}\\ {u} \end{bmatrix} \begin{bmatrix} {R / L}&{C_u / L}\\ {C_u / J}&{0} \end{bmatrix} \begin{bmatrix} {i}\\ {u} \end{bmatrix} + \begin{bmatrix} {1 / L}&{0} \\ {C_u / J}&{0} \end{bmatrix} \begin{bmatrix} {u}\\ {M_z} \end{bmatrix}$

(17)

Prenosové funkcie:

Prenos riadenia pre $\omega$ :

$F_{1} (s) = \frac{\omega (s)}{U (s)} = \frac{K_M}{T_e T_m s^2 + T_m s +1}$

(18)

Prenos poruchy pre $\omega$ :

$F_{2} (s) = \frac{\omega (s)}{M_Z (s)} = \frac{\frac{R_m}{C_u ^2} (1 + T_e s)}{T_e T_m s^2 + T_m s +1}$

(19)

Prenos riadenia prúdu:

$F_{3} (s) = \frac{I (s)}{U (s)} = \frac{\frac{T_M s}{R_m}}{T_e T_m s^2 + T_m s +1}$

(20)

Prenos poruchy prúdu:

$F_{4} (s) = \frac{\omega (s)}{U (s)} = \frac{\frac{1}{C_u}}{T_e T_m s^2 + T_m s +1}$

(21)

Prechodové charakteristiky prúdu pre prípad, že charakteristický polynóm má jednoduché
póly:

$\omega (t) = K_M \{ 1 - \frac{T_1}{T_2 - T_1} e ^{- \frac{t}{T_1}} +\frac{T_2}{T_2 - T_1} e ^{- \frac{t}{T_2}} \} U$

(22)

$i(t) = \frac{T_M}{R_M} \{ \frac{1}{T_1 - T_2} (e^{- \frac{t}{T_1}} - e^{- \frac{t}{T_2}} ) \} U$

(23)

Vhodným upravením rovníc dostaneme momentovú aj záťažovú charakteristiku pre konštantný magnetický tok:

$M_m = \frac{C_u}{R_m} U - \frac{C_u ^2}{R_m} \omega$

(24)

$\omega = \frac{1}{C_u} U - \frac{R_m}{C_u ^2} M_z$

(25)

čomu zodpovedajú grafy na obr. 7.

Obr. 7 Momentová a záťažová charakteristika JM pre konštantný $\Phi$

Sériový jednosmerný motor

Po pripojení sériového motora k napájaciemu napätiu začne pretekať prúd rotora taktiež budiacim vinutím statora (obr. 9). Záberový moment takéhoto motora je veľký a preto je na motore takmer celé napájacie napätie. Po rozbehu sa zväčšuje indukované napätie v rotory a napätie na vinutí sa zmenšuje. Zmenšuje sa aj celkový prúd prechádzajúci motorom a taktiež aj jeho točivý moment. So zväčšujúcou sa rýchlosťou otáčok sa zmenšuje aj magnetické pole statora. Aj napriek tomu sa rýchlosť otáčania zväčšuje, zmenšuje sa indukované napätie v rotore, čo má za dôsledok ďalšie zvýšenie otáčok. Ak nieje motor zaťažený, môže sa rýchlosť otáčania dostať na kritickú hodnotu a ohroziť tým mechanickú pevnosť rotora. Po zaťažení sa prúd znovu v motore rýchle zväčšuje, zväčšuje sa magnetické pole statora a rýchlosť otáčania sa zmenšuje. Sériový motor sa preto so svojimi vlastnosťami hodí hlavne tam, kde požadujeme veľký záberový moment pri rozbehu (obr. 8), avšak kde súčasne po rozbehu vyhovuje rýchlosť otáčania závislá na záťaži.

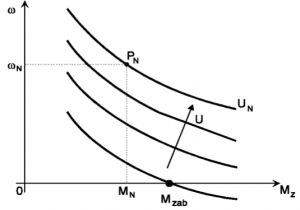
Obr. 8 Záťažové charakteristiky jednosmerného sériového motora

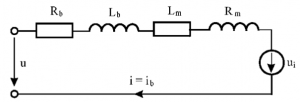
Obr. 9 Náhradná elektrická schéma

Dynamický model sériového motora je opísaný nasledovnými vzťahmi:

$u = (R_m + R_b) i + (L_m + L_b) \frac{d i}{d t} +u_i$

(26)

$u_i = C' \Phi \omega$

(27)

$u_i = C' \Phi i$

(28)

$M_m - M_z = M_d = J_m \frac{d \omega}{d t}$

(29)

Derivačný jednosmerný motor

Po pripojení motora k napájaciemu napätiu dosiahne magnetické pole na statore okamžite maximálnu hodnotu a bude stále v celom rozsahu otáčania. V kotve sa rýchlo s rýchlosťou otáčania zväčšuje indukované napätie, takže sa rýchlo zväčšuje prúd i krútiaci moment. Keď dosiahne indukované napätie veľkosť napájacieho napätia rýchlosť otáčania sa ustáli. Rozdiel je daný len úbytkom napätí na vinutí kotvy, spôsobený prúdom, ktorý cez ňu preteká. Pretože je magnetické pole statora konštantné, vplyvom zaťaženia sa nemení, nemení sa ani indukované napätie v závislosti od záťaže a otáčky sú konštantné.

Kompaudný jednosmerný motor

U tohto typu motora sa využívajú vlastnosti sériového a derivačného motora a získame tak charakteristiku vyhovujúcu konkrétnej aplikácii. Môže prevládať veľký záberový moment (vlastnosť sériového motora), alebo môže mať konštantnú rýchlosť otáčania (motor s paralelným budením). Tieto vlastnosti sa dosahujú zmenou závitov vinutia sériového či paralelného budenia, alebo zaraďovaním rezistorov do jednotlivých vinutí, eventuálne prepínaním časti vinutí.

Literatúra

Žalman, M.: Akčné členy, STU, Bratislava 2003
Mravec R.: Elektrické stroje a prístroje 2, Alfa Bratislava, 1976 3

O časopise

Meta

RSS

Analýza vlastností akčných členov pre jednosmerné motory

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív