V poslednej dobe sa čoraz častejšie spomínajú netradičné výpočtové metódy, ktoré napodobňujú procesy prirodzenej evolúcie. Využívajú sa na riešenie rôznych typov zložitých matematických, technických, ekonomických, ale aj iných praktických problémov, pri ktorých súčasné výpočtové metódy nedávajú uspokojivé výsledky, prípadne nie sú použiteľné vôbec. Tieto nové typy metód sa zastrešujú názvom – „evolučné výpočtové metódy“.

Z evolučnej teórie o vzniku a vývoji života vieme, že všetky formy života sa vyvíjali postupne od najjednoduchších až po najzložitejšie. Prirodzená evolúcia je proces, pri ktorom sa postupom času, aj keď to trvalo viac než 3 miliardy rokov, z najjednoduchších jednobunkových organizmov vyvinul človek. Pritom tento proces nie je riadený, čiže neexistuje tu žiadna spätná väzba, ktorá by bola schopná “korigovať” genetický kód novo vznikajúcich jedincov v závislosti od úspechu alebo neúspechu ich predchodcov . Jedinou hybnou silou, ktorá posúva vývoj dopredu je schopnosť silnejších jedincov prežiť v konkurenčnom boji o potravu alebo o získanie partnera, prípadne schopnosť niektorých jedincov prispôsobiť sa zmenám životných podmienok, pokiaľ iní sa prispôsobiť nedokážu a vyhynú. Tí úspešnejší potom odovzdávajú svoju genetickú informáciu ďalším generáciám. Tento evolučný proces je vo svojej podstate jednoduchý, ale na druhej strane je veľmi robustný a výkonný. Platí rovnako pre jednobunkové živočíchy ako aj pre človeka, ktorý pozostáva z asi 6000 miliárd buniek.

Inšpirovaní evolučným procesom začali matematici, biológovia, neskôr aj informatici čoraz častejšie nastolovať otázku, či by sa nedal tento „mechanizmus“ napodobňovať a využívať pri riešení vo všeobecnosti nebiologických problémov. Dvere týmto snahám, ako tomu bolo aj v mnohých iných oblastiach, otvorila až výkonná výpočtová technika. Bez nej by nebolo možné simulovať tisíce alebo milióny evolučných cyklov, ktoré prebiehali v prírode. V druhej polovici dvadsiateho storočia boli podľa vzoru prirodzenej evolúcie na rôznych pracoviskách vo svete pri riešení odlišných problémov vytvorené viaceré, ale v istých črtách podobné prístupy. V Nemecku v polovici šesťdesiatych rokov boli pri optimalizácii konštrukčných úloh I.Rechenbergom a H.P.Schwefelom vyvíjané tzv. „evolučné stratégie“. Lawrence Fogel v tom období v USA pri modelovaní a návrhu automatov vyvíjal techniku pod názvom „evolučné programovanie“. Za vznik „genetických algoritmov“, ktoré majú dnes široké použitie pri optimalizácii sú považované práce skupiny pod vedením Johna Hollanda z Michiganskej University v USA v 70. rokoch dvadsiateho storočia. Historicky mladšie „genetické programovanie“ je evolučný prístup určený najmä na automatizovaný vývoj a optimalizáciu programov, funkcionálnu regresiu alebo strojové učenie. Za jeho autora je považovaný John Koza (USA) na prelome 80. a 90. rokov. Všetky takéto smery sa dnes zvyknú zastrešovať pojmom “evolučné algoritmy”.

Jedným z najvýznamnejších predstaviteľov evolučných algoritmov (EA) s veľmi širokým uplatnením sú genetické algoritmy (GA). GA sú univerzálnym stochastickým prehľadávacím alebo optimalizačným prístupom, ktorý je v ohraničenom priestore prípustných riešení daného problému schopný nájsť alebo sa aspoň priblížiť ku globálnemu optimu. Uplatňuje sa pritom z prírody vypozorovaný princíp prežitia najsilnejších resp. najprispôsobivejších jedincov a nevyhnutnosť zániku najslabších, neživotaschopných resp. neprispôsobivých.

Princíp činnosti

Keby sme mali princíp GA vyjadriť dvomi vetami, mohli by sme povedať, že pracujú s populáciou viacerých riešení, kde pôsobením genetických operácii “kríženia” a “mutácie” priebežne vznikajú úspešnejšie a menej úspešné riešenia. Tie úspešné majú väčšiu šancu byť vybrané, postupovať v evolúcii ďalej a odovzdávať svoje vlastnosti ďalším generáciám, na úkor menej úspešných jedincov, ktoré zanikajú.

Trocha detailnejšie vysvetlenie mechanizmu GA je nasledovné (obr.1). Zdôraznime, že sa jedná o optimalizačnú metódu, čiže našou úlohou je nájsť najlepšie možné riešenie daného problému v ohraničenom priestore možných riešení. Algoritmus pracuje so skupinou potenciálnych riešení – s tzv. “populáciou”. Každé potenciálne riešenie je pritom reprezentované usporiadanou množinou parametrov alebo hodnôt, ktoré charakterizujú jeho vlastnosti. Prvky tejto množiny sa nazývajú “gény” a môžu byť binárneho, celočíselného, reálnečíselného, symbolového alebo kombinovaného typu, v závislosti od charakteru daného problému. Sú usporiadané (zakódované) do postupnosti, ktorá sa nazýva “reťazec” alebo “chromozóm”. Počiatočná populácia reťazcov v prvom výpočtovom cykle (tzv. “generácii”) sa získa spravidla náhodným vygenerovaním ich génov v rámci uvažovaných ohraničení. Pre každé riešenie, ktoré sa dekóduje z reťazca do existujúceho počítačového modelu sa vyčísli výpočtom, počítačovou simuláciou, atď. hodnota účelovej funkcie – tzv. “fitness”. Fitness je vlastne miera vhodnosti alebo úspešnosti daného reťazca alebo “jedinca”. Všetky jedince populácie sa navzájom porovnajú a potom sa vyberie skupina jedincov, ktoré sa nezmenené dostanú do novej populácie. Tiež sa vyberie druhá skupina jedincov, ktorá je určená na inováciu. V tejto skupine sa vytvoria náhodné páry reťazcov, s ktorými sa uskutoční genetická operácia “kríženie”. Potom sa na tejto skupine realizuje ešte “mutácia”. Takto zmodifikované jedince potom dokompletujú novú populáciu, ktorá sa stane objektom rovnakého postupu v ďalšej generácii. Pritom je dôležité, že pri výbere do oboch skupín majú najväčšiu pravdepodobnosť “prežitia” najúspešnejšie jedince, ale istú šancu majú aj menej úspešné jedince. Ak sa uvedený postup opakuje mnohokrát – počas mnohých generácií, riešenie konverguje k najlepšiemu riešeniu – ku globálnemu optimu. Pod pojmom “mnohokrát” si môžeme predstaviť číslo 100, 1000 alebo aj 1 milión. Závisí to od povahy a zložitosti riešeného problému. Beh algoritmu sa môže ukončiť po dosiahnutí požadovaného resp. prijateľného riešenia, alebo po ukončení určeného počtu generácií.

Spomínali sme tri typy operácií – kríženie, mutácia a výber. Operácia kríženia náhodne skombinuje gény dvoch rodičov do jedného alebo viacerých potomkov. Pri bežnom spôsobe kríženia sa dva rodičovské reťazce rozdelia na jednom alebo viacerých náhodných miestach (oba reťazce na rovnakých) a potomkovia získajú striedavo každú druhú časť takto oddelených podreťazcov od každého z rodičov (obr.2,3). Operácia mutácie náhodne zmení náhodne zvolené gény náhodne vybraných jedincov (obr.4). Čitateľ nemôže prehliadnuť, že základnou črtou týchto algoritmov je náhodnosť. Poznamenajme ešte, že existujú viaceré typy kríženia aj mutácie. Spôsobov výberu jedincov do nových populácií je tiež niekoľko druhov, líšia sa mierou preferovania najúspešnejších jedincov oproti náhodne vybraným jedincom. Voľba genetických operácií môže byť ovplyvnená typom riešeného problému.

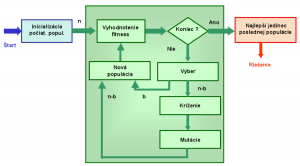
Obr.1 Bloková schéma genetického algoritmu

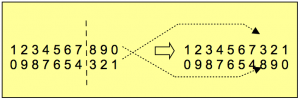
Obr.2 Príklad jednobodového kríženia dvoch reťazcov

Obr.3 Viacbodové kríženie dvoch reťazcov

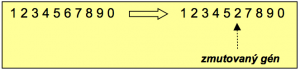
Obr.4 Príklad mutácie celočíselného reťazca

Vlastnosti

GA sa od väčšiny “konvenčných” optimalizačných metód líšia niektorými znakmi:

• sú schopné vyviaznuť z okolia lokálneho extrému a približovať sa ku globálnemu extrému
• uskutočňujú paralelné prehľadávanie vo viacerých smeroch súčasne
• nevyžadujú pomocné informácie o vývoji riešenia, ako je napr. gradient účelovej funkcie
• intenzívne využívajú stochastické procesy
• sú schopné riešiť optimalizačné problémy s desiatkami až stovkami premenných
• sú pomerne jednoducho aplikovateľné na široké spektrum optimalizačných problémov
• patria k časovo resp. výpočtovo najnáročnejším riešeniam.

Charakteristickou črtou evolučných algoritmov je, že sú výpočtovo teda časovo veľmi náročné, čo ale pri dnešnej výkonnosti výpočtovej techniky prestáva byť relevantný problém. Teoretickou nevýhodou môže byť fakt, že konvergencia riešenia sa matematicky dokazuje len veľmi obtiažne. Praktické skúsenosti s konvergenciou výpočtu však sú takmer vždy veľmi uspokojivé.

Možnosti použitia

Evolučné alebo genetické algoritmy sa dajú použiť na riešenie veľmi širokého spektra úloh. Zopakujme, že podmienkou je schopnosť sformulovať účelovú (kriteriálnu) funkciu, ktorá sa má minimalizovať alebo maximalizovať. Pri minimalizácii sa obyčajne jedná o minimalizáciu odchýlky (chyby) od požadovaného stavu, minimalizáciu spotreby energie, paliva alebo nákladov, o minimalizáciu nežiaducich účinkov a podobne. Pri maximalizácii môže ísť o maximalizáciu účinnosti, výkonu, zisku atď. Ďalšou podmienkou použitia EA je počítačová reprezentácia optimalizovaného problému, čiže existencia matematického modelu realizovaného v počítači alebo počítačová simulácia daného procesu (deja), ktorého optimálne riešenie hľadáme. To znamená, že pre ľubovoľný bod prehľadávaného priestoru, teda pre ľubovoľné potenciálne riešenie vieme počítačom vyčísliť hodnotu jeho účelovej funkcie – ohodnotiť ho z hľadiska úspešnosti, z hľadiska miery splnenia požadovaného cieľa. Pritom vôbec nezáleží na type daného procesu, ktorý môže byť fyzikálneho, chemického, biologického, ekonomického, alebo hoci sociologického charakteru. Veľmi zjednodušene povedané, optimalizovaný problém z pohľadu evolučného algoritmu je čierna skrinka, ktorá poskytuje veľké množstvo viac alebo menej zmysluplných možností riešenia, pričom každú z nich vieme navonok ohodnotiť napríklad číselne alebo aspoň porovnať jej úspešnosť voči iným možnostiam. Pod optimalizáciou možno potom chápať hľadanie takej možnosti (sady parametrov, štruktúry vnútorných väzieb a pod.), ktorá najlepšie splňuje určené požiadavky. Aj keď to na prvý pohľad nie je vždy zrejmé, takto možno úlohu postaviť aj pre veľmi veľkú množinu problémov, ktoré vo svojej pôvodnej formulácii nie sú klasickými optimalizačnými úlohami. Často aj úplne bežné matematické a iné problémy je možné veľmi jednoducho transformovať na minimalizačné resp. maximalizačné úlohy.

Medzi problémy, ktoré sú použitím konvenčných optimalizačných prístupov riešiteľné len ťažko alebo dokonca vôbec, a ktoré môžu byť typickými aplikáciami genetických, resp. evolučných algoritmov, patria napr. hľadanie globálnych extrémov nelineárnych a multimodálnych funkcií (funkcií mnohých premenných), ťažké kombinatorické alebo grafovo orientované problémy, mnohoparametrové problémy, pri ktorých zložitosť narastá s počtom premenných exponenciálne alebo faktoriálovo, úlohy s kombinovanými typmi premenných, úlohy s veľkým počtom rôznych typov obmedzení (nerovnosti, rovnosti, logické podmienky) a podobne.

Na tomto mieste nie je možné ani účelné vymenúvať mnohé úspešné aplikácie genetických alebo evolučných výpočtových techník, ale pre ilustráciu alebo pre inšpiráciu stručne uveďme aspoň niektoré. Významným poľom pôsobnosti sú inžinierske aplikácie. GA môžu byť silným nástrojom pri optimalizácii elektrických obvodov, pri optimalizácii prevádzky elektrizačnej sústavy, pri návrhu antén a filtrov, pri statickej optimalizácii technologických procesov alebo pri návrhu regulačných obvodov. Zo strojárskych aplikácií spomeňme napríklad návrh prevodoviek, alebo návrh rezných plánov. Známe je využitie GA pri optimalizácii motorov Boeingu 777, kedy sa zdanlivo malou konštrukčnou úpravou získala na dané pomery mimoriadne významná úspora paliva až 2,5 %. Toto predstavuje pri jednom lietadle za rok úsporu 2 miliónov dolárov. Výnimkou nie sú ani aplikácie v stavebníctve pri optimalizácii konštrukcie budov, cestných komunikácií alebo sietí. Veľmi široké uplatnenie nachádzajú evolučné techniky pri riešení ekonomických problémov, ktoré často predstavujú zložité úlohy lineárneho alebo nelineárneho programovania s mnohými obmedzeniami alebo logistické úlohy.

Veľmi perspektívnou oblasťou evolučných výpočtových techník je genetické programovanie. Známe sú napríklad aplikácie, keď touto technikou bol počítačom vytvorený program na hranie šachu. V inej oblasti sa genetické programovanie využíva na optimalizáciu a návrh štruktúr ako sú napríklad logické automaty alebo integrované obvody až na úrovni mikroprocesorov.

Takže, na záver by sme mohli skonštatovať, že použitie evolučných výpočtových techník je veľmi jednoduché a efektívne. Všetko, čo potrebujeme je počítačový model daného problému vo forme výpočtu, simulácie, vyhonotenia vlastností atď. a potom už len trocha trpezlivosti. Riešenie prinesie darvinovská evolúcia realizovaná elektronickou rýchlosťou.

---

Slovenská technická univerzita, Fakulta elektrotechniky a informatiky, Ilkovičova 3, 812 19 Bratislava.