Analýza vlastností synchrónneho motora

28. Október, 2009, Autor článku: Tesár Richard, Elektrotechnika, Strojárstvo
Ročník 2, číslo 10 Pridať príspevok

motorcek V predchádzajúcom článku sme sa venovali úvodu do synchrónnych motorov. Popísali sme si základné rozdelenie synchrónnych motorov, ich konštrukciu a princíp činnosti. V dnešnej časti si popíšeme matematický aparát, ktorý stojí za synchrónnymi motormi.

3 Vznik kruhového otáčavého poľa a priama a spätná Clarcova transformácia

Vznik kruhového rovinného otáčavého poľa tvorí fyzikálny základ striedavých strojov. Pre názornú predstavu treba vychádzať z toho, že rovinu tvorí priečny rez stroja. Na vytvorenie kruhového poľa treba generovať dva budiace signály, ktoré sú fázovo posunuté o 90° a pôsobia v smere osi x a y (obr. 4).

$u_x = u_m * \cos \omega _s * t$
$u_y = u_m * \sin \omega _s * t$	(1)

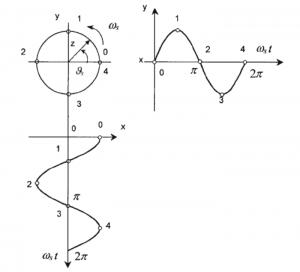
Obr.4 Vznik otáčavého poľa v rovine x –y

Pre zavedenie ďalších pojmov je vhodné stotožniť rovinu x – y s komplexnou rovinou, kde x je reálna os a y je imaginárna os komplexnej roviny. Budiace signály ux, uy sú zložky rovinného, časovo premenlivého vektora vyjadreného v kartézskych súradniciach vzťahom

$\hat{u} = u_x + ju_y = u_m * (\cos \omega _s * t + j * \sin \omega _s * t)$

(2)

alebo v polárnych súradniciach

$\hat{u} = u_m * e ^{j \omega _s * t} = u_m * e^{j \vartheta _s}$

(3)

$\vartheta _s = \int \omega _s dt$

(4)

kde $\vartheta _s$ je argument vektora, $u_m$ je modul vektora.

Vektor napätia možno zobraziť v komplexnej rovine podľa obr. 5.

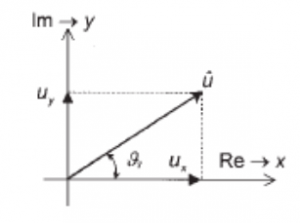
Obr.5 Vektorový diagram vektora napätia

Otáčavé kruhové pole sa môže vytvoriť m – fázovým symetrickým systémom napätí kde m ≥ 2, m = 2, 3, 5, 7 (vynechávajú sa párne násobky čísla 2, 3, 5, 7). Trojfázový symetrický systém napätí nech je vyjadrený vzťahom:

$u _a = U_m * \cos (\omega _e t)$
$u _b = U_m * \cos (\omega _e t - 120 ^\circ)$
$u _c = U_m * \cos (\omega _e t + 120 ^\circ)$	(5)

kde U_m je amplitúda napájacieho napätia a $\omega _e$ je uhlová frekvencia napájacieho napätia.

Pre symetrickú sústavu platí vzťah

$u_a + u_b + u_c = 0$

(6)

Pre zavedenie ďalších pojmov stotožníme rovinu priečneho rezu motora s komplexnou rovinou. Pozdĺžnu os vinutia a stotožníme s reálnou osou komplexnej roviny.

V trojfázovom systéme vyjadríme mechanické natočenie statorových vinutí nasledovnými jednotkovými vektormi v komplexnej rovine.

$\hat{I}_a = 1$
$\hat{I}_b = 1 * \hat{a} ^2 = e ^{j 120 ^{\circ}} = \cos 120 ^{\circ} + j \sin 120 ^{\circ} = - \frac{1}{2} + j \frac{\sqrt{3}}{2}$
$\hat{I}_c = 1 * \hat{a} ^2 = e ^{j 240 ^{\circ}} = \cos 240 ^{\circ} + j \sin 240 ^{\circ} = - \frac{1}{2} - j \frac{\sqrt{3}}{2}$	(7)

Vektor napätia daného vinutia v komplexnej rovine je rovný súčinu napätia vinutia s príslušným jednotkovým vektorom (7). Výsledný vektor napätia v komplexnej rovine je rovný súčtu vektorov napätí jednotlivých vinutí.

$\hat{u} = 1* (u_a + \hat{a} * u_b + \hat{a} ^2 * u_c)$

(8)

Ak pravú stranu rovnice (8) vynásobíme číslom k, potom môžeme vyjadriť všeobecný tvar pre lineárnu transformáciu z 3/2.

Všeobecný tvar pre lineárnu transformáciu z 3/2

$\hat{u} = k (u_a + \hat{a} * u_b + \hat{a} ^{2} * u_c) =$
$= k u_a + k (- \frac{1}{2} + j \frac{\sqrt{3}}{2}) u_b + k (- \frac{1}{2} - j \frac{\sqrt{3}}{2}) u_c = u_{s \alpha} + j u_{s \beta}$	(9)

Zo vzťahu (9) vyplýva, že vektor napätia vytvorený trojfázovým statorovým symetrickým systémom môžeme vytvoriť aj pomocou dvojfázového statorového symetrického systému.

Priama a spätná Clarkova transformácia

Nasledujúce vzťahy vyjadrujú ekvivalentný prepočet medzi trojfázovým symetrickým statorovým systémom (a, b, c) a ekvivalentným dvojfázovým symetrickým statorovým systémom ( $\alpha , \beta$ ).

Ak os $\alpha$ stotožníme s reálnou osou komplexnej roviny (rovnako ako os a), tak použitím vzťahu (9) dostávame prepočtové vzťahy pre priamu Clarcovu transformáciu 3/2.

$u_{s \alpha} = k \frac{3}{2} u_a$

(10)

$u_{s \beta} = k \frac{\sqrt{3}}{2} (u_b -u_c)$

(11)

Použitím vzťahov (6) a (10 a (11) dostávame prepočtové vzťahy pre spätnú Clarcovu transformáciu 2/3.

$u_{a} = \frac{2}{3 k} u_{s \alpha}$

(12)

$u_{b} = - \frac{1}{3 k} u_{s \alpha} + \frac{1}{k \sqrt{3}} u_{s \beta}$

(13)

$u_{c} = - \frac{1}{3 k} u_{s \alpha} - \frac{1}{\sqrt{3}} u_{s \beta}$

(14)

V prípade Clarcovej transformácie je prepočtový koeficient k rovný hodnote

$k = \frac{2}{3}$

(15)

4 Transformácia statorového systému $\alpha , \beta$ do fiktívneho systému rotora d, q.

Súradnicový systém m – fázových veličín striedavého motora môže byť viazaný – orientovaný buď na časti stroja, (stator, rotor) alebo čo sa už ťažšie chápe aj na vektor stavových veličín motora (magnetický tok, prúd, napätie), ktoré sa otáčajú synchrónnou uhlovou rýchlosťou v rovine tvoriacej priečny rez stroja.

Základné súradnicové systémy sú:

„s“ súradnicový systém pevne viazaný na stator s → ( $\alpha, \beta$ )

„r“ súradnicový systém pevne spojený s rotorom r → (d, q)

„w_k“ súradnicový systém orientovaný na vektory stavových veličín w_k → (1, 2)

Zavedenie rôznych súradnicových systémov takto vyžaduje riešiť problém ich vzájomného vzťahu. Pri otáčaní rotora SMPM t.j. pri variabilnej hodnote uhla natočenia $\vartheta$ sa mení magnetická väzba (vzájomná indukčnosť) medzi statorovými vinutiami a PM v rotore. Transformáciou statorového systému rovníc v súradnicovom systéme $\alpha , \beta$ do súradnicového systému d, q pevne spojeného s rotorom dostaneme vzťahy, v ktorých sa magnetické väzby medzi vinutiami a PM nemenia (nie sú závislé od uhla natočenia rotora $\vartheta$ ).Tým vytvoríme fiktívne statorové vinutia d, q spojené s rotorom.

Striedavé statorové veličiny sa tak transformujú na jednosmerné veličiny. V ustálenom stave budú transformované veličiny konštantné.

Súradnicové systémy statora ( $\alpha , \beta$ ) a rotora (d, q) majú svoj počiatok umiestnený v počiatku komplexnej roviny v bode (0, j0). Os d je totožná s pozdĺžnou osou rotora (osou radiálne uloženého PM). Rotorový súradnicový systém (d, q) pevne spriahnutý s rotorom sa voči statorovému súradnicovému systému ( $\alpha , \beta$ ) otáča uhlovou rýchlosťou $\omega (t)$ . Uhol natočenia rotora voči statoru je potom daný vzťahom:

$\vartheta (t) = \int \omega (t) dt$

(16)

Na Obr. 6 sú znázornené súradnicové systémy ( $\alpha , \beta$ ) a (d, q).

Pre ľubovoľný komplexný vektor platia vzťahy

$\hat{u} _s ^R = \hat{u} _s ^S * e^{- j \vartheta}$

(17)

$\hat{u} _s ^S = \hat{u} _s ^R * e^{j \vartheta}$

(18)

Komplexný vektor vyjadrený v súradnicovom systéme rotora d, q má tvar:

$\hat{u} _s ^R = u_{d} + j u_{q}$

(19)

Komplexný vektor vyjadrený v súradnicovom systéme statora $\alpha , \beta$ má tvar:

$\hat{u} _s ^S = u_{s \alpha} + j u_{s \beta}$

(20)

Pre vektory vyjadrené v zložkovom tvare dostávame vzájomné prepočtové vzťahy:

$u_{s \alpha} = u_d \cos (\vartheta) - u_q \sin (\vartheta)$
$u_{s \beta} = u_d \sin (\vartheta) - u_q \cos (\vartheta)$	(21)

$u_{d} = u_{s \alpha} \cos (\vartheta) - u_{s \beta} \sin (\vartheta)$
$u_{q} = u_{s \alpha} \sin (\vartheta) - u_{s \beta} \cos (\vartheta)$	(22)

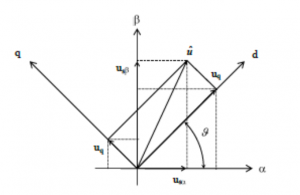
Obr. 6 Zobrazenie komplexného vektora v súradnicovom systéme statora ( $\alpha , \beta$ ) a v súradnicovom systéme rotora (d, q) natočeného o uhol $\vartheta$ voči statorovému systému

5 Matematický model SMPM v súradnicovom systéme rotora (d, q)

V súradnicovom systéme d, q sú statorové vinutia transformované na fiktívne statorové vinutia umiestnené v osiach d a q. Os d je vždy totožná s pozdĺžnou osou rotora Obr. 7.

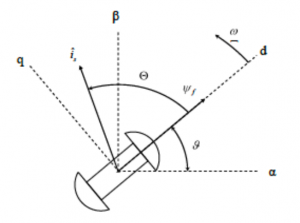
Obr. 7 Vektorový diagram riadiacich veličín SMPM

Pre vektory magnetického toku $\hat{\psi _s}$ , statorového napätia $\hat{u} _s$ a statorového prúdu $\hat{i _s}$ v komplexnej rovine spriahnutej s rotorom (d, q) platia vzťahy:

$\hat{\psi} _s = \psi _d + j \psi _q$

(23)

$\hat{u} _s = u _d + j u _q$

(24)

$\hat{i} _s = i _d + j i _q$

(25)

Vektory komplexne združené označujeme pomocou $(*) : \hat{\psi} ^{*} _{s} = \psi _d - j \psi _q$ .

Z obrázku Obr. 8 vidieť znázornenie elektromagnetického systému SMPM v sústave d, q.

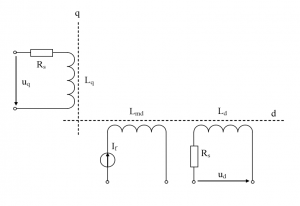
Obr. 8 Náhradná elektrická schéma SMPM v sústave rotora d, q

Budiaci obvod je nahradený permanentnými magnetmi, ktorý je v schéme vyjadrený zdrojom konštantného budiaceho prúdu I_f .

Pre zložky magnetických tokov platia nasledujúce vzťahy:

$\psi _d = L_d i_d + L_{md} i_f = L_d i_d + \psi _f$

(26)

$\psi _f = L_{md} i_f$

(27)

$\psi _q = L_q i_q$

(28)

Hodnotu konštantného budiaceho magnetického toku $\psi _f$ od permanentných magnetov je možné určiť aj pomocou vzťahu:

$\psi _f = \frac{2 * K_t}{3 * p'}$

(29)

Kde K_t predstavuje momentovú konštantu motora a p’ počet pólových dvojíc synchrónneho motora.

Z rovníc (26) až (28) vyplývajú rovnice pre prúdy fiktívnych vinutí v smere osi d, q

$i_d = \frac{1}{L_d} (\psi _d - \psi _f) = \frac{1}{L_d} (\psi _d - L_{md} i_f)$

(30)

$i_q = \frac{1}{L_q} \psi _q$

(31)

Elektromagnetický systém SM obsahuje rovnicu pre statorový obvod, ktorá má v sústave rotora (d, q) tvar:

$\hat{u} _s = R_s \hat{i} _s + \frac{d \hat{\psi _s}}{d t} + j \omega _e \hat{\psi _s} = u_d + j u_q$

(32)

V zložkovom tvare:

$u_d = R_s i_d + \frac{d \psi_d}{d t} - \omega _e \psi _q$

(33)

$u_q = R_s i_q + \frac{d \psi_q}{d t} - \omega _e \psi _d$

(34)

Rovnica pre elektromagnetický moment:

$M_m = \frac{3}{2} p' \Im (\hat{i}_s * \hat{\psi} _s ^*) = \frac{3}{2} p' (\psi_d i_q -\psi_q i_d)$

(35)

Z predchádzajúcich vzťahov je na Obr. 9 zostavená bloková schéma elektrickej časti SMPM vo fiktívnom rotorovom súradnicovom systéme d, q.

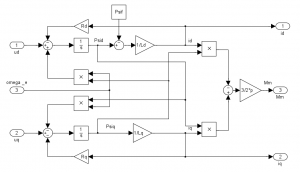
Obr. 9 Bloková schéma elektrickej časti SMPM vo fiktívnom rotorovom súradnom systéme d, q

Doplňujúca mechanická časť SMPM Obr. 10 sa pripája na výstupný moment elektrickej časti SMPM. Táto dekompozícia na elektrickú a mechanickú časť je vhodná pre účely simulácie, kedy do mechanickej časti môžeme zakomponovať aj prípadný pracovný mechanizmus so záťažovým momentom (prevodovka, navíjačka, extrúder, …). Konštanta B, predstavuje koeficient viskózneho trenia, blok suchého trenia slúži na modelovanie suchého trenia M_z0.

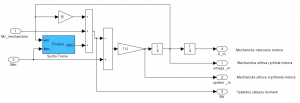
Obr. 10 Mechanický subsystém SMPM

Literatúra

Dal Y. Ohm: Dynamic model of PM synchronous motor, Drivetech Inc., Virginia
http://www.drivetechinc.com/articles/IM97PM_Rev1forPDF.pdf
Žalman, M.: Akčné členy, STU, Bratislava 2003

O časopise

Meta

RSS

Analýza vlastností synchrónneho motora

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív