 The paper deals with the robust decentralized controller design in the frequency domain for stable plants. Nominal and robust stability conditions under a decentralized IMC controller are developed. An illustrative example is included.
The paper deals with the robust decentralized controller design in the frequency domain for stable plants. Nominal and robust stability conditions under a decentralized IMC controller are developed. An illustrative example is included.
1 INTRODUCTION
PID controllers are standard and well-proven solution for the majority of industrial applications. Over the years, a plenty of PID tuning rules were developed see e.g. (Šulc and Vítečková, 2005).
In this paper decentralized PID controller design approaches are developed for stable systems and further extended to satisfy robust stability conditions in terms of unstructured uncertainty developed in (Kozáková A., Veselý, 2005; Kozáková and Veselý, 2009). The approach is IMC structure-based and applicable just for stable plants; an innovation brought about by its development is derivation of robust stability conditions in terms of a decentralized IMC controller.
The paper is organized as follows: preliminaries and problem formulation are given in Section 2, robust decentralized IMC controller for stable plants is addressed in Section 3. In Section 4, a detailed robust decentralized PID controller design procedure is illustrated on an example in Section 5. Conclusions are drawn at the end of the paper.
2 PRELIMINARIES AND PROBLEM FORMULATION
The Internal Model Control (IMC) structure was introduced as an alternative to the classic feedback structure. Its main advantage is that closed-loop stability is guaranteed simply by choosing a stable IMC controller.
Consider the simplified block diagram of the IMC structure (Morari and Zafiriou, 1989) depicted in Fig. 1
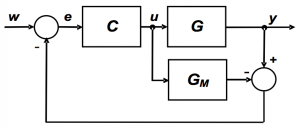
Fig. 1 – IMC structure
where 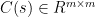 denotes the controller,
denotes the controller,  is the plant and
is the plant and  is the plant model. Exact knowledge of the output y is assumed. If the model is exact, i.e. if
is the plant model. Exact knowledge of the output y is assumed. If the model is exact, i.e. if 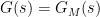 then
then
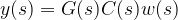 , , |
(1) |
Relationship with the standard feedback structure in Fig. 2 is obtained simply by comparing outputs from both structures
![[G (s) R (s) + I]^{-1} G (s) R (s) = G (s) R (s) [G (s) R (s) + I]^{-1} G (s) R (s) = G (s) R (s)](http://s0.wp.com/latex.php?latex=%5BG+%28s%29+R+%28s%29+%2B+I%5D%5E%7B-1%7D+G+%28s%29+R+%28s%29+%3D+G+%28s%29+R+%28s%29+&bg=ffffff&fg=000000&s=1) , , |
(2) |
where  is the controller
is the controller
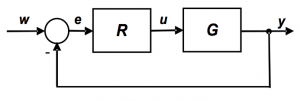
Fig. 2 – Standard feedback configuration
The standard controller 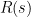 and the IMC controller
and the IMC controller  are related through
are related through
![R (s) = [I - C (s) G (s)]^{-1} C (s) R (s) = [I - C (s) G (s)]^{-1} C (s)](http://s0.wp.com/latex.php?latex=R+%28s%29+%3D+%5BI+-+C+%28s%29+G+%28s%29%5D%5E%7B-1%7D+C+%28s%29+++&bg=ffffff&fg=000000&s=1) , , |
(3) |
If  is stable and
is stable and 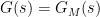 , the standard feedback system with controller (3) is internally stable if and only if
, the standard feedback system with controller (3) is internally stable if and only if  is stable. In such a case (3) is a simple parameterization of all stabilizing controllers
is stable. In such a case (3) is a simple parameterization of all stabilizing controllers 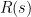 in terms of stable
in terms of stable 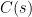 . Thus, instead of searching for
. Thus, instead of searching for 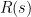 it is possible and simpler to search for
it is possible and simpler to search for 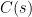 (Morari and Zafiriou, 1989).
(Morari and Zafiriou, 1989).
When designing a controller a major source of difficulty is plant model inaccuracy; hence uncertainty models are to be used which means that instead of a single model a class  of perturbed models is to be considered. Denote
of perturbed models is to be considered. Denote 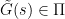 any perturbed plant model and
any perturbed plant model and 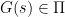 the nominal plant model. A simple uncertainty model is obtained using unstructured uncertainty
the nominal plant model. A simple uncertainty model is obtained using unstructured uncertainty 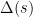 . Three uncertainty forms are commonly used: additive
. Three uncertainty forms are commonly used: additive  , multiplicative input
, multiplicative input 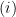 and multiplicative output
and multiplicative output 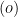 uncertainties.
uncertainties.
Standard feedback configuration with unstructured uncertainty of any type can be rearranged to obtain the general  structure in Fig. 3 where
structure in Fig. 3 where  represents the nominal model and
represents the nominal model and ![\Delta (s) : \sigma_{max} [\Delta (j \omega)] \leq 1 \Delta (s) : \sigma_{max} [\Delta (j \omega)] \leq 1](http://s0.wp.com/latex.php?latex=%5CDelta+%28s%29+%3A+%5Csigma_%7Bmax%7D+%5B%5CDelta+%28j+%5Comega%29%5D+%5Cleq+1+&bg=ffffff&fg=000000&s=0) the normalized perturbation.
the normalized perturbation.
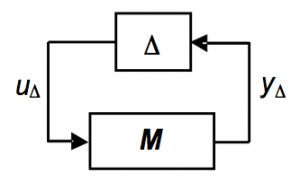
Fig. 3 –  structure
structure
Robust stability condition for unstructured perturbations is formulated in terms of stability of the  system: if both the nominal system
system: if both the nominal system  is stable (nominal stability) and the normalized perturbation
is stable (nominal stability) and the normalized perturbation 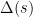 is stable, closed-loop stability is guaranteed for
is stable, closed-loop stability is guaranteed for
![\sigma_{max} [M (j \omega)] < 1, \quad \forall \, \omega [/latex] ,</td> <td style="width:20px; text-align:center;">(4)</td> </tr> </table> <p align="justify">For individual uncertainty types <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />M = l_k M_k \sigma_{max} [M (j \omega)] < 1, \quad \forall \, \omega [/latex] ,</td> <td style="width:20px; text-align:center;">(4)</td> </tr> </table> <p align="justify">For individual uncertainty types <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />M = l_k M_k](http://s0.wp.com/latex.php?latex=%5Csigma_%7Bmax%7D+%5BM+%28j+%5Comega%29%5D+%3C+1%2C+%5Cquad+%5Cforall+%5C%2C+%5Comega+%26%2391%3B%2Flatex%26%2393%3B+%2C%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%284%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cp+align%3D%22justify%22%3EFor+individual+uncertainty+types+%5Blatex+size%3D%220%22%5DM+%3D+l_k+M_k+&bg=ffffff&fg=000000&s=1) , ,  in particular in particular
- for additive uncertainty
- for multiplicative input uncertainty
- for multiplicative output uncertainty
In view of (5), (6, (7) condition (4) reads as follows
![\sigma_{max} (M_k (s)) < \frac{1}{\mid l_k (s) \mid}, \quad k = a, i, o [/latex] </td> <td style="width:20px; text-align:center;">(8)</td> </tr> </table> <p align="justify"><strong>Problem Formulation</strong>. For the uncertain plant <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\tilde{G} (s) \sigma_{max} (M_k (s)) < \frac{1}{\mid l_k (s) \mid}, \quad k = a, i, o [/latex] </td> <td style="width:20px; text-align:center;">(8)</td> </tr> </table> <p align="justify"><strong>Problem Formulation</strong>. For the uncertain plant <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\tilde{G} (s)](http://s0.wp.com/latex.php?latex=%5Csigma_%7Bmax%7D+%28M_k+%28s%29%29+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_k+%28s%29+%5Cmid%7D%2C+%5Cquad+k+%3D+a%2C+i%2C+o+%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%288%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cp+align%3D%22justify%22%3E%3Cstrong%3EProblem+Formulation%3C%2Fstrong%3E.+For+the+uncertain+plant+%5Blatex+size%3D%220%22%5D%5Ctilde%7BG%7D+%28s%29+&bg=ffffff&fg=000000&s=1) a decentralized controller is to be designed a decentralized controller is to be designed
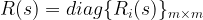 |
(9) |
where 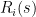 is the transfer function of the i – th local controller. The designed controller has to guarantee stability of the controlled plant over the entire operating range specified by (5), (6), (7), i.e. robust stability (RS). is the transfer function of the i – th local controller. The designed controller has to guarantee stability of the controlled plant over the entire operating range specified by (5), (6), (7), i.e. robust stability (RS).
3 MAIN RESULTS
With a view of designing a decentralized (diagonal) controller, the nominal plant  is split into the diagonal part is split into the diagonal part 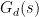 and the off-diagonal part and the off-diagonal part  , i.e. , i.e.
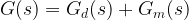 |
(10) |
Then, the controller (3) with a decentralized structure is
![R (s) = [I - C (s) G_d (s)]^{-1} C (s) R (s) = [I - C (s) G_d (s)]^{-1} C (s)](http://s0.wp.com/latex.php?latex=R+%28s%29+%3D+%5BI+-+C+%28s%29+G_d+%28s%29%5D%5E%7B-1%7D+C+%28s%29+&bg=ffffff&fg=000000&s=1) |
(11) |
where  is a suitably chosen stable diagonal matrix. is a suitably chosen stable diagonal matrix.
3.1 Guaranteeing robust stability
To guarantee robust stability using the IMC structure it is necessary to suitably recast the  robust stability condition (8). Uncertainties in the three standard forms (5), (6), (7) will be considered. robust stability condition (8). Uncertainties in the three standard forms (5), (6), (7) will be considered.
For the centralized IMC controller and different uncertainty types, substituting (3) in (8) yields
- for the additive uncertainty
![\sigma_{max} [C (s)] < \frac{1}{\mid l_a (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(12)</td> </tr> </table> <li>for the multiplicative input uncertainty </li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} [C (s) G (s)] < \frac{1}{\mid l_i (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(13)</td> </tr> </table> <li>for the multiplicative output uncertainty </li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} [G (s) C (s)] < \frac{1}{\mid l_o (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(14)</td> </tr> </table> </ul> <p align="justify">For the <em>decentralized </em>controller (DC) (11) the above robust stability conditions develop into <ul> <li>for the additive uncertainty</li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} \{ [C^{-1} (s) + G_m (s)]^{-1} \} < \frac{1}{\mid l_a (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(15)</td> </tr> </table> <li>for the multiplicative input uncertainty</li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} \{ [C^{-1} (s) + G_m (s)]^{-1} G (s) \} < \frac{1}{\mid l_i (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(16)</td> </tr> </table> <li>for the multiplicative output uncertainty</li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} \{ G (s) [C^{-1} (s) + G_m (s)] \} < \frac{1}{\mid l_o (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(17)</td> </tr> </table> </ul> <p align="justify"><strong>3. 2 Guaranteeing nominal stability </strong> <p align="justify">According to the General robust stability theorem formulated for the <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />M - \Delta \sigma_{max} [C (s)] < \frac{1}{\mid l_a (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(12)</td> </tr> </table> <li>for the multiplicative input uncertainty </li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} [C (s) G (s)] < \frac{1}{\mid l_i (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(13)</td> </tr> </table> <li>for the multiplicative output uncertainty </li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} [G (s) C (s)] < \frac{1}{\mid l_o (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(14)</td> </tr> </table> </ul> <p align="justify">For the <em>decentralized </em>controller (DC) (11) the above robust stability conditions develop into <ul> <li>for the additive uncertainty</li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} \{ [C^{-1} (s) + G_m (s)]^{-1} \} < \frac{1}{\mid l_a (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(15)</td> </tr> </table> <li>for the multiplicative input uncertainty</li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} \{ [C^{-1} (s) + G_m (s)]^{-1} G (s) \} < \frac{1}{\mid l_i (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(16)</td> </tr> </table> <li>for the multiplicative output uncertainty</li> <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma_{max} \{ G (s) [C^{-1} (s) + G_m (s)] \} < \frac{1}{\mid l_o (s) \mid} [/latex] </td> <td style="width:20px; text-align:center;">(17)</td> </tr> </table> </ul> <p align="justify"><strong>3. 2 Guaranteeing nominal stability </strong> <p align="justify">According to the General robust stability theorem formulated for the <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />M - \Delta](http://s0.wp.com/latex.php?latex=%5Csigma_%7Bmax%7D+%5BC+%28s%29%5D+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_a+%28s%29+%5Cmid%7D+%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2812%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cli%3Efor+the+multiplicative+input+uncertainty+%3C%2Fli%3E+%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D%5Csigma_%7Bmax%7D+%5BC+%28s%29+G+%28s%29%5D+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_i+%28s%29+%5Cmid%7D+%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2813%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cli%3Efor+the+multiplicative+output+uncertainty+%3C%2Fli%3E+%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D%5Csigma_%7Bmax%7D+%5BG+%28s%29+C+%28s%29%5D+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_o+%28s%29+%5Cmid%7D+%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2814%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3C%2Ful%3E+%3Cp+align%3D%22justify%22%3EFor+the+%3Cem%3Edecentralized+%3C%2Fem%3Econtroller+%28DC%29+%2811%29+the+above+robust+stability+conditions+develop+into+++%3Cul%3E+%3Cli%3Efor+the+additive+uncertainty%3C%2Fli%3E+%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D%5Csigma_%7Bmax%7D+%5C%7B+%5BC%5E%7B-1%7D+%28s%29+%2B+G_m+%28s%29%5D%5E%7B-1%7D+%5C%7D+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_a+%28s%29+%5Cmid%7D++++%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2815%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cli%3Efor+the+multiplicative+input+uncertainty%3C%2Fli%3E+%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D%5Csigma_%7Bmax%7D+%5C%7B+%5BC%5E%7B-1%7D+%28s%29+%2B+G_m+%28s%29%5D%5E%7B-1%7D+G+%28s%29+%5C%7D+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_i+%28s%29+%5Cmid%7D++++%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2816%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cli%3Efor+the+multiplicative+output+uncertainty%3C%2Fli%3E+%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D%5Csigma_%7Bmax%7D+%5C%7B+G+%28s%29+%5BC%5E%7B-1%7D+%28s%29+%2B+G_m+%28s%29%5D+%5C%7D+%3C+%5Cfrac%7B1%7D%7B%5Cmid+l_o+%28s%29+%5Cmid%7D++++%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2817%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3C%2Ful%3E+%3Cp+align%3D%22justify%22%3E%3Cstrong%3E3.+2++Guaranteeing+nominal+stability+%3C%2Fstrong%3E++%3Cp+align%3D%22justify%22%3EAccording+to+the+General+robust+stability+theorem+formulated+for+the+%5Blatex+size%3D%220%22%5DM+-+%5CDelta+&bg=ffffff&fg=000000&s=1) structure (Morari and Zafiriou, 1989), stability of structure (Morari and Zafiriou, 1989), stability of  , i.e. nominal stability is the prerequisite for robust stability. , i.e. nominal stability is the prerequisite for robust stability.
Next, the additive type uncertainty is considered, development for other uncertainty types is similar.
Consider nominal stability of the uncertain system described with additive uncertainty in the IMC structure, i.e. stability of (5) transformed to (15).
![M_a (s) = [C ^{-1} (s) + G_m (s)]^{-1} M_a (s) = [C ^{-1} (s) + G_m (s)]^{-1}](http://s0.wp.com/latex.php?latex=M_a+%28s%29+%3D+%5BC+%5E%7B-1%7D+%28s%29+%2B+G_m+%28s%29%5D%5E%7B-1%7D+++&bg=ffffff&fg=000000&s=1) |
(18) |
Further manipulations yield
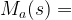 ![- \frac{adj [C^{-1} (s) + G_m (s)]}{\det [C^{-1} (s)] \, \det [I + C (s) G_m (s)]} - \frac{adj [C^{-1} (s) + G_m (s)]}{\det [C^{-1} (s)] \, \det [I + C (s) G_m (s)]}](http://s0.wp.com/latex.php?latex=-+%5Cfrac%7Badj+%5BC%5E%7B-1%7D+%28s%29+%2B+G_m+%28s%29%5D%7D%7B%5Cdet+%5BC%5E%7B-1%7D+%28s%29%5D+%5C%2C+%5Cdet+%5BI+%2B+C+%28s%29+G_m+%28s%29%5D%7D+++&bg=ffffff&fg=000000&s=2) |
(19) |
Because  is supposed to be a stable diagonal matrix, the polynomial is supposed to be a stable diagonal matrix, the polynomial ![\det [C^{-1} (s)] \det [C^{-1} (s)]](http://s0.wp.com/latex.php?latex=%5Cdet+%5BC%5E%7B-1%7D+%28s%29%5D+&bg=ffffff&fg=000000&s=0) is stable and stability of is stable and stability of 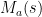 depends on the stability of the factor depends on the stability of the factor ![\det [I + C (s) G_m (s)]. \det [I + C (s) G_m (s)].](http://s0.wp.com/latex.php?latex=%5Cdet+%5BI+%2B+C+%28s%29+G_m+%28s%29%5D.+&bg=ffffff&fg=000000&s=0) Applying to it the Small gain theorem (Morari and Zafiriou; Skogestad and Postlethwaite, 1997) the sufficient stability condition reads as Applying to it the Small gain theorem (Morari and Zafiriou; Skogestad and Postlethwaite, 1997) the sufficient stability condition reads as
![\sigma _{max} [C (s) G_m (s)] < 1 [/latex] </td> <td style="width:20px; text-align:center;">(20)</td> </tr> </table> <p align="justify">or using the singular value properties. <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma _{max} [C (s)] < [/latex] <img src='http://s0.wp.com/latex.php?latex=++%5Cfrac%7B1%7D%7B%5Csigma_%7Bmax%7D+%5BG_m+%28s%29%5D%7D+++&bg=ffffff&fg=000000&s=2' alt=' \frac{1}{\sigma_{max} [G_m (s)]} ' title=' \frac{1}{\sigma_{max} [G_m (s)]} ' class='latex' /> </td> <td style="width:20px; text-align:center;">(21)</td> </tr> </table> <p align="justify">Considering <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />C (s) \sigma _{max} [C (s) G_m (s)] < 1 [/latex] </td> <td style="width:20px; text-align:center;">(20)</td> </tr> </table> <p align="justify">or using the singular value properties. <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />\sigma _{max} [C (s)] < [/latex] <img src='http://s0.wp.com/latex.php?latex=++%5Cfrac%7B1%7D%7B%5Csigma_%7Bmax%7D+%5BG_m+%28s%29%5D%7D+++&bg=ffffff&fg=000000&s=2' alt=' \frac{1}{\sigma_{max} [G_m (s)]} ' title=' \frac{1}{\sigma_{max} [G_m (s)]} ' class='latex' /> </td> <td style="width:20px; text-align:center;">(21)</td> </tr> </table> <p align="justify">Considering <img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' />C (s)](http://s0.wp.com/latex.php?latex=%5Csigma+_%7Bmax%7D+%5BC+%28s%29+G_m+%28s%29%5D+%3C+1+++%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2820%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cp+align%3D%22justify%22%3Eor+using+the+singular+value+properties.++%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D%5Csigma+_%7Bmax%7D+%5BC+%28s%29%5D+%3C+%26%2391%3B%2Flatex%26%2393%3B+%3Cimg+src%3D%27http%3A%2F%2Fs0.wp.com%2Flatex.php%3Flatex%3D%2B%2B%255Cfrac%257B1%257D%257B%255Csigma_%257Bmax%257D%2B%255BG_m%2B%2528s%2529%255D%257D%2B%2B%2B%26bg%3Dffffff%26fg%3D000000%26s%3D2%27+alt%3D%27++%5Cfrac%7B1%7D%7B%5Csigma_%7Bmax%7D+%26%2391%3BG_m+%28s%29%26%2393%3B%7D+++%27+title%3D%27++%5Cfrac%7B1%7D%7B%5Csigma_%7Bmax%7D+%26%2391%3BG_m+%28s%29%26%2393%3B%7D+++%27+class%3D%27latex%27+%2F%3E+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2821%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cp+align%3D%22justify%22%3EConsidering+%5Blatex+size%3D%220%22%5DC+%28s%29+&bg=ffffff&fg=000000&s=1) a diagonal matrix a diagonal matrix 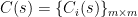 with with 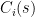 being stable transfer functions, condition (21) can be rewritten as being stable transfer functions, condition (21) can be rewritten as
 ![\mid C_i (s) \mid < \frac{1}{\sigma _{max} [G_m (s)]}, \quad i = 1, ... , m [/latex] </td> <td style="width:20px; text-align:center;">(22)</td> </tr> </table> <p align="justify">Consider a decentralized PID controller with local controllers in the form <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' /> R_i = \frac{r_2 s^2 + r_1 s + r_0}{k_r s} \mid C_i (s) \mid < \frac{1}{\sigma _{max} [G_m (s)]}, \quad i = 1, ... , m [/latex] </td> <td style="width:20px; text-align:center;">(22)</td> </tr> </table> <p align="justify">Consider a decentralized PID controller with local controllers in the form <table style="width:100%;"> <tr> <td style="text-align:center;"><img src='http://s0.wp.com/latex.php?latex&bg=ffffff&fg=000000&s=0' alt='' title='' class='latex' /> R_i = \frac{r_2 s^2 + r_1 s + r_0}{k_r s}](http://s0.wp.com/latex.php?latex=%5Cmid+C_i+%28s%29+%5Cmid+%3C+%5Cfrac%7B1%7D%7B%5Csigma+_%7Bmax%7D+%26%2391%3BG_m+%28s%29%26%2393%3B%7D%2C+%5Cquad+i+%3D+1%2C+...+%2C+m++%26%2391%3B%2Flatex%26%2393%3B+%3C%2Ftd%3E+%3Ctd+style%3D%22width%3A20px%3B+text-align%3Acenter%3B%22%3E%2822%29%3C%2Ftd%3E+%3C%2Ftr%3E+%3C%2Ftable%3E++++%3Cp+align%3D%22justify%22%3EConsider+a+decentralized+PID+controller+with+local+controllers+in+the+form++%3Ctable+style%3D%22width%3A100%25%3B%22%3E+%3Ctr%3E+%3Ctd+style%3D%22text-align%3Acenter%3B%22%3E%5Blatex+size%3D%221%22%5D+R_i+%3D+%5Cfrac%7Br_2+s%5E2+%2B+r_1+s+%2B+r_0%7D%7Bk_r+s%7D++&bg=ffffff&fg=000000&s=1) |
(23) |
Tuning parameter  will used to stabilize the full closed-loop system in the sense of (22) and ensuring robust stability (15), (16), (17). will used to stabilize the full closed-loop system in the sense of (22) and ensuring robust stability (15), (16), (17).
3.3 Robust decentralized controller design procedure for stable systems
- Nominal model calculating;
- Controller design for each subsystems of nominal model using any SISO approach;
- Once subsystems controllers are known, tuning parameters
 are adjusted, so that the nominal stability condition (22) and any of the robust stability conditions (15), (16), (17) are met simultaneously; are adjusted, so that the nominal stability condition (22) and any of the robust stability conditions (15), (16), (17) are met simultaneously;
4 EXAMPLE
Consider plant with two inputs and two outputs represented engine-generator identified in three working points
Nominal model of this plant was calculated:
Assume that input-output pairing was done and diagonal pairing is recommended. For diagonal elements PI controllers were designed using D-curves method.
Tuning parameters 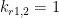
Decentralized feedback controller ![R (s) = \big [ \begin{smallmatrix} {R_1} & {0} \\ {0} & {R_2} \end{smallmatrix} \big ] R (s) = \big [ \begin{smallmatrix} {R_1} & {0} \\ {0} & {R_2} \end{smallmatrix} \big ]](http://s0.wp.com/latex.php?latex=R+%28s%29+%3D+%5Cbig+%5B+%5Cbegin%7Bsmallmatrix%7D+%7BR_1%7D+%26+%7B0%7D+%5C%5C++%7B0%7D+%26+%7BR_2%7D+%5Cend%7Bsmallmatrix%7D+%5Cbig+%5D+&bg=ffffff&fg=000000&s=0) was calculated into IMC form was calculated into IMC form ![C (s) = R (s) [I + G_d R]^{-1} C (s) = R (s) [I + G_d R]^{-1}](http://s0.wp.com/latex.php?latex=C+%28s%29+%3D+R+%28s%29+%5BI+%2B+G_d+R%5D%5E%7B-1%7D+&bg=ffffff&fg=000000&s=0) and nominal stability condition (22) was tested (fig. 4). and nominal stability condition (22) was tested (fig. 4).
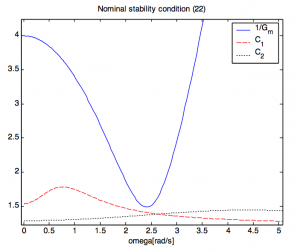
Fig. 4 Nominal stability condition (22)
Nominal stability condition is passed. Robust stability condition (12) is depicted in Fig. 5.
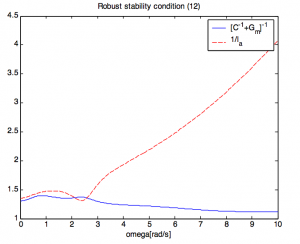
Fig. 5 Robust stability condition (12)
From fig. 5 it is evident that robust stability condition is not passed so tuning parameters 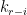 has to be changed. has to be changed.
Increasing of first tuning parameter on value 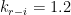 robust stability was satisfied (Fig. 6) robust stability was satisfied (Fig. 6)
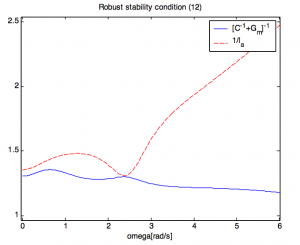
Fig. 6 Robust stability condition with 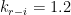
Resulting sets  of closed-loop poles proves the stability in three working points. of closed-loop poles proves the stability in three working points.
5 CONCLUSION
The paper deals with the robust decentralized controller design in the frequency domain for stable plants. Nominal and robust stability conditions under a decentralized IMC controller are developed. An illustrative example is included.
ACKNOWLEDGEMENT
This work was supported by the Scientific Grant Agency of the Ministry of Education of the Slovak Republic and the Slovak Academy of Sciences under Grants No. 1/0544/09 and 1/0822/08/4.
REFERENCES
- Morari M., Zafiriou E., (1989) Robust process control. Prentice Hall.
- Skogestad S, Postlethwaite I., (1997) Multivariable feedback control: analysis and design. John Wiley
- Kozáková A., Veselý V. (2005) A frequency domain design technique for robust decentralized controllers. Preprints of the 16th IFAC World Congress. Prague, Czech Republic July 3-8, p. Mo-E21-TO/6.
- Kozáková A., Veselý V., (2009) Design of robust decentralized controllers using the M- structure robust stability conditions, Int. Journal of Systems Science.
- Šulc B., Vítečková, M., (2004) Theory and practice of control loops design. ČVUT, Praha (in Czech).
Co-authors of this paper are Vojtech Veselý and Alena Kozáková, Slovak University of Technology, Faculty of Electrical Engineering and Information Technology, Ilkovičova 3, 812 19 Bratislava.
Napísať príspevok
| | | |
 Pridať príspevok
Pridať príspevok
 The paper deals with the robust decentralized controller design in the frequency domain for stable plants. Nominal and robust stability conditions under a decentralized IMC controller are developed. An illustrative example is included.
The paper deals with the robust decentralized controller design in the frequency domain for stable plants. Nominal and robust stability conditions under a decentralized IMC controller are developed. An illustrative example is included. denotes the controller,
is the plant and
is the plant model. Exact knowledge of the output y is assumed. If the model is exact, i.e. if
then
is the controller

and the IMC controller
are related through
is stable and
, the standard feedback system with controller (3) is internally stable if and only if
is stable. In such a case (3) is a simple parameterization of all stabilizing controllers
in terms of stable
. Thus, instead of searching for
it is possible and simpler to search for
(Morari and Zafiriou, 1989).
of perturbed models is to be considered. Denote
any perturbed plant model and
the nominal plant model. A simple uncertainty model is obtained using unstructured uncertainty
. Three uncertainty forms are commonly used: additive
, multiplicative input
and multiplicative output
uncertainties.
structure in Fig. 3 where
represents the nominal model and
the normalized perturbation.
system: if both the nominal system
is stable (nominal stability) and the normalized perturbation
is stable, closed-loop stability is guaranteed for






