Biometrické metódy pre rozpoznávanie obrazov ľudských tvárí

01. Marec, 2010, Autor článku: Ban Jozef, Elektrotechnika, Informačné technológie, Študentské práce
Ročník 3, číslo 3 Pridať príspevok

Screen shot 2010-01-31 at 10.21.13 AM Práca sa zaoberá metódami pre rozpoznávanie obrazov ľudských tvárí, MLP, RBF a SVM. Metódy testujeme na databáze vytvorenej na Massachusetts Institute of Technology o rozmeroch obrazov 16×15, 32×30 a 64×60, pričom sa snažíme pomocou vhodného hľadania a nastavovania parametrov jednotlivých metód o čo najpriaznivejšie výsledky testu.

1. Úvod

Rozpoznávanie ľudskej tváre je aj pre súčasnú výpočtovú techniku zložitá úloha a stále vyvíjaná a zdokonaľovaná metóda identifikácie jednotlivca. Pre nás ľudí úplne prirodzená vlastnosť rozpoznať známeho človeka, známu ľudskú tvár je pri iných uhloch natočenia tváre, rôznych pozadiach, alebo vzdialenosti pre výpočtovú techniku neľahký problém, ktorý sme sa pomocou metód pre rozpoznávanie obrazov ľudských tvárí snažili vyriešiť. Snahou bolo pomocou metód MLP, RBF a SVM dosiahnuť čo najlepšie výsledky správnej verifikácie ľudskej tváre.

2. Biometria

Biometria [1], [2] je obor, ktorý skúma človeka a iné živé organizmy podľa jedinečných merateľných charakteristík. Jednotlivé biometrické znaky (črty, biometriky) človeka sa zdigitalizujú – prevedú do elektronickej podoby a je s nimi možné narábať, ako s jedinečným kódom. Tieto údaje sú prenositeľné a overiteľné [3].

Biometriu môžeme výhodne využiť pre rýchlu a spoľahlivú identifikáciu osôb. Výhodou biometrických čŕt na rozdiel od iných spôsobov identifikácie ľudí je ich univerzálnosť (sledovaný znak majú všetci ľudia), jedinečnosť (každý jedinec má črtu jednoznačne rozdielnu) a dá sa jej porovnaním jednoznačne identifikovať, stálosť (tieto črty sú v čase nemenné).

Biometrické bezpečnostné systémy môžu pracovať vo dvoch základných režimoch a to identifikácia (napr. rozpoznávanie jedinca v dave) a verifikácia (overenie identity jedinca). Základnou vlastnosťou biometrie je jej presnosť.

2.1. V súčasnosti používané biometrické metódy

História biometrie je dlhá viac ako 130 rokov. Používanie biometrických metód v minulosti malo svoje miesto hlavne v kriminalistike. V súčasnosti používanie týchto metód, na identifikáciu osôb, má všestranný charakter. Čoraz viac sa môžeme stretávať sich využitím či už na hraničných priechodoch, pri ochrane počítačov, sietí, budov, majetku, transakcií, alebo tiež napr. v stravovacích systémoch.

Pre biometrickú identifikáciu sa používajú hlavne tieto metódy:

Odtlačky prstov
Geometria ruky
Očná dúhovka
Ľudská tvár
Ďalšie často používane metódy identifikácie sú napr. hlas, DNA ale i pach, geometria ucha a iné.

2.2. Porovnanie biometrických metód

Biometriu môžeme rozdeliť na biometriu telesnú (fyziologickú) a biometriu správania. Do statickej anatomickej biometrie patrí: odtlačok prstu, tvár, termogram tváre, dúhovka oka, sietnica oka, geometria ruky, termogram ruky, tvar ucha, telesný pach, štruktúra nechtu, forenzná DNA, dentálny obraz. Do dynamickej biometrie správania sa radí: hlas, gestikulácia tváre, dynamika podpisu, dynamika stisku kláves a chôdza [4].

U biometrických vlastností definujeme nasledujúce kritériá:

univerzalita (každá osoba musí túto vlastnosť mať)
jedinečnosť (žiadne dve osoby nesmú mať rovnakú vlastnosť)
konštantnosť (vlastnosť zostáva s časom nemenná)
získateľnosť (vlastnosť je kvantitatívne merateľná)
výkonnosť (vlastnosť sa nesmie zmeniť a ani zostarnúť)
akceptácia (ochota ľudí pre nasnímanie danej vlastnosti)
bezpečnosť (náročnosť vytvorenia falzifikátu danej vlastnosti)
cena (cenové náklady na systém)

Tab.1. Porovnanie existujúcich biometrických metód [5]

Biometrická metóda	Univerzálnosť	Unikátnosť	Trvalosť	Výkon	Prijateľnosť
Tvár	vysoká	nízka	stredná	nízky	vysoká
Odtlačok prsta	stredná	vysoká	vysoká	vysoký	stredná
Geometria ruky	stredná	stredná	stredná	stredný	stredná
Strojopis	nízka	nízka	nízka	nízky	stredná
Žili na rukách	stredná	stredná	stredná	stredný	stredná
Očné dúhovky	vysoká	vysoká	vysoká	vysoký	nízka
Sietnica	vysoká	vysoká	stredná	vysoký	nízka
Podpis	nízka	nízka	nízka	nízky	vysoká
Hlas	stredná	nízka	nízka	nízky	vysoká
Termograf	vysoká	vysoká	nízka	stredný	vysoká
Pach	vysoká	vysoká	vysoká	nízky	stredná
DNA	vysoká	vysoká	vysoká	vysoký	nízka
Geometria ucha	stredná	stredná	vysoká	stredný	vysoká

Na základe štúdia súčasných metód, ako aj dohode s vedúcim práce, sme sa rozhodli pre rozpoznávanie obrazov ľudských tvárí ato pomocou troch metód, MLP, RBF a SVM.

3. Viacvrstvový perceptrón

Prvou metódou, ktorú sme používali pri simuláciách rozpoznávania obrazov ľudských tvári, je viacvrstvový perceptrón (MLP, „multi-layer perceptron“) [6].

Takýto druh siete sa skladá z vrstvy vstupných prvkov (vstupná vrstva), ktoré distribuujú vstupné signály do siete, z jednej alebo viacerých skrytých vrstiev výpočtových prvkov a z výstupnej vrstvy výpočtových prvkov. Vstupné signály sa v sieti šíria dopredným smerom postupne od vrstvy k vrstve.

3.1. Vlastnosti viacvrstvového perceptrónu

Existencia jednej (obr. 1) alebo viac spätných vrstiev umožňujú sieti naučiť sa komplikované úlohy, pretože vyberajú zo vstupných vzoriek najdôležitejšie príznaky. Názov skrytý neurón znamená, že takýto neurón nie je súčasťou vstupnej, ani výstupnej vrstvy, čiže zvonku siete je neprístupný. Dôležitou charakteristikou je tiež vysoký stupeň prepojenia siete, určený synapsami siete. Ďalšou dôležitou charakteristikou je, že model každého neurónu v sieti obsahuje na výstupe nelinearitu. Veľmi dôležité je, že táto nelinearita musí byť hladká, t.j. všade diferencovateľná.

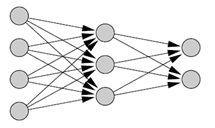
Obr. 1 MLP s jednou skrytou vrstvou

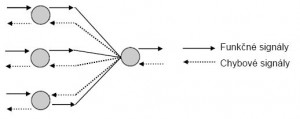
Obr. 2 Funkčné a chybové signály v MLP

V znázornenej časti viacvrstvového perceptrónu (obr. 2) je možné pozorovať funkčné a chybové signály. Funkčný signál sa šíri dopredne, prichádza zo vstupu siete a končí na výstupe siete ako výstupný signál. Chybový signál vznikne vo výstupných neurónoch počas trénovania a šíri sa spätne.

Skryté aj výstupné neuróny robia počas trénovania dva výpočty. Prvý je výpočet funkčného signálu, ktorý je výstupom neurónu. Je vyjadrený ako nelineárna funkcia vstupných signálov a synaptických váh spojených s týmto neurónom. Druhým výpočtom je odhad okamžitého gradientového vektora, t.j. gradientu chybového povrchu vzhľadom na váhy, ktoré sú pripojené k danému vektoru. Tento vektor je potrebný pre fázu spätného šírenia chýb.

3.2. Algoritmus spätného šírenia

Viacvrstvový perceptrón sa trénuje pomocou učiteľa. Používa algoritmus spätného šírenia [6]. Chybový signál na výstupe neurónu j pri privedení n-tej trénovacej vzorky (iterácií) je definovaný ako:

$\displaystyle e _j (n) = d _j (n) - y _j (n)$

(1)

pričom predpokladáme, že neurón j je výstupným neurónom, d_j(n) je žiadaná a y_j(n) aktuálna odpoveď. Vnútorná aktivita neurónu j je:

$\displaystyle v _j (n) = \sum ^{p} _{i = 0} w _{j i} (n) y _i (n)$

(2)

kde p je celkový počet vstupov neurónu j a w_p(n) je synaptická váha spájajúca výstup neurónu i so vstupom neurónu j pri iterácií n. Funkčný signál na výstupe neurónu j pri iterácií n je:

$\displaystyle y _j (n) = \varphi _j (v _j (n))$

(3)

Algoritmus spätného šírenia upravuje váhu w_p(n) o hodnotu $\Delta$ w_p(n), ktorá je úmerná okamžitému gradientu $d \epsilon (n) / d w _{j i} (n)$ .

Po ďalších úpravách môžeme pre algoritmus spätného šírenia zhodnotiť nasledovné skutočnosti:

Úprava $\Delta w_j (n)$ pre váhu spojenia neurónu i a neurónu j je definovaná delta pravidlom:

$\displaystyle \left( \begin{smallmatrix} \acute{u} prava \\ v \acute {a} hy \\ {\Delta w _{\eta} (n)} \end{smallmatrix}\right) = \left( \begin{smallmatrix} parameter \\ r \acute{y} chlosti \\ u \check{c} enia \quad \eta \end{smallmatrix}\right) * \left( \begin{smallmatrix} lok \acute{a} lny \\ gradient \\ \delta _j (n) \end{smallmatrix}\right) * \left( \begin{smallmatrix} vstupn \acute{y} \, sign \acute{a} l \\ neur \acute{o} nu \, j \\ y _i (n) \end{smallmatrix}\right)$

(4)

3.3. Kritérium pre ukončenie učenia

Pri použití algoritmu spätného šírenia sa nedá jednoznačne určiť či už skonvergoval. Často používaným kritériom je, že po každej epoche sa sieť testuje z hľadiska generalizácie. Učenie sa skončí, keď sieť generalizuje primerane našim požiadavkám alebo sieť dosiahla svoje maximum v schopnosti generalizovať. MLP reprezentuje mapovanie z p - rozmerného euklidovského priestoru vstupov do q – rozmerného euklidovského priestoru výstupov, kde p je počet vstupných neurónov a q počet výstupných neurónov viacvrstvového perceptrónu [6].

4. RBF sieť

Pod RBF sieťou [7] rozumieme druh neurónovej siete, ktorý ako prechodovú funkciu používa radiálnu bázovú funkciu. Takéto siete sú z aproximačného hľadiska prirodzené, pretože aproximujeme funkciami, ktoré ovplyvnia výslednú funkciu len v okolí centra príslušnej RBF jednotky a nie v celom rozsahu funkcie.

V mnohých prípadoch sa pomocou RBF sietí dosahujú lepšie výsledky ako pri použití sietí so sigmoidálnymi prechodovými funkciami (MLP – viacvrstvový perceptrón). Jednou z možných príčin je aj fakt, že RBF prechodové funkcie lepšie odpovedajú receptívnym poliam skutočných neurónov [8], [9].

4.1. Štruktúra RBF siete

Formálne môžeme RBF siete vyjadriť nasledujúcim vzťahom:

$\displaystyle f (x) = w _0 + \sum ^{m} _{i = 1} w _i h _i (x)$

(5)

Každý z n komponentov vstupného vektora x je vstupnou hodnotou pre m RB funkcií. Celkový výstup siete je potom lineárnou kombináciou výstupov RBF prvkov a váh w.

Obr. 3: RBF sieť [10]

4.2. Trénovanie RBF

Trénovacia množina pre RBF sieť pozostáva zo vstupno-výstupných párov $(x _k , d _k) \, k = 1, \ldots \, , N$ kde $x _k \in R ^p$ je vstup a $d _k \in R ^q$ je žiadaná odpoveď.

RBF sieť je trénovaná v troch krokoch [6]:

Prvým krokom je určenie centier skrytých prvkov, ktoré sú reprezentované váhami medzi vstupnou a skrytou vrstvou. Veľmi jednoduchým riešením tohto problému je náhodný výber n₀ bodov z daných vstupov, ktoré nastavíme ako hodnoty centier. Iný triviálny prístup generuje rovnomerné rozdelenie centier vo vstupnom priestore.

Je však žiaduce, aby centrá vystihovali štruktúru vstupných dát – to si vyžaduje pre nastavenie centier použiť dômyselnejšie algoritmy. Táto úloha spadá do kategórie samoorganizovaného učenia.
Druhý (voliteľný) krok slúži na nastavenie prídavných parametrov RBF.

Pripomeňme veľmi často používanú (bola použitá aj pri našich experimentoch) gaussovsku radiálnu funkciu:

$\displaystyle \phi (x) = exp \Bigg ( - \frac{\parallel x - c \parallel ^2}{\sigma ^2} \Bigg )$ (6)

Jej parameter $\sigma$ reprezentuje šírku funkcie $\phi$ riadi radiálnu oblasť okolo centra c v ktorej má určitý skrytý prvok rozumnú odpoveď. Šírky funkcií ovplyvňujú generalizačné schopnosti siete – čím sú menšie, tým horšia generalizácia sa dá očakávať. Parameter $\sigma$ , bol predmetom našich testov.

V treťom kroku učenia sa nastavujú váhy w , minimalizáciou chybovej funkcie:

$\displaystyle E _3 (W) = \frac{1}{2} \sum ^N _{l = 1} \parallel d _l - f (x_1) \parallel ^2 =$
$\displaystyle = \frac{1}{2} \sum ^N _{l = 1} \sum ^q _{k = 1} (d _{k l} - f _k (x _l)) ^2$	(7)

kde $f _k (x _l) = y _l$ je odpoveď (výstup) siete na vstup $x_l$ , $f _k (x _l ) = y _{kl}$ je odpoveď (výstup) k-teho výstupného prvku na vstup $x _l$ , $W$ je matica $w_{s r}$ – čiže s prvkami $w_{r s}, \, s = 1 \ldots , \, q$ a $r = 1 , \, \ldots , \, n_0$ . Ak prvú deriváciu $E_3$ podľa $w_{r s}$ položíme rovnú nule, dostaneme vzťah

$\displaystyle w _{r s} = \sum ^{n _0} _{j = 1} [\Phi ^{+}] _{j r} \Bigg ( \sum ^{N} _{l = 1} \phi _j (x _l) d _{k l} \Bigg )$

(8)

kde matica $\Phi$ je definovaná ako

$\displaystyle [\Phi]_{jr} = \sum ^{N} _{l = 1} \phi _j (x _l) \phi _r (x _l)$

(9)

5. SVM

Stroj s podpornými vektormi (suport vector machine, SVM) [11], [12] je metóda získavania optimálnej hranice medzi dvoma príkladmi jednotlivých tried vo vektorovom priestore nezávisle na pravdepodobnostnom rozdelení trénovacích vektorov v triedach. Podstata je veľmi jednoduchá, lokalizujeme hranicu. Tá je najvzdialenejšia od vektorov, ktoré sú najbližšie od hranice oboch tried. Hoci tento jednoduchý nápad nie je ničím novým, aj v dnešnej dobe sa mu venuje veľká pozornosť. Je to dôsledkom zavedenia tzv. kernelových metód, ktoré sú ekvivalentné transformácii vektorového priestoru s cieľom lokalizácie nelineárnej hranice.

5.1. Kernelová metóda

Metóda jemného rozpätia (soft margin) je nadstavbou SVM v rámci lineárnych metód. Kernelová metóda je metóda hľadania nelineárnych hraníc. Základný koncept kernelovej metódy je transformácia vektorového priestoru na viacrozmerný priestor. Uvažujeme lineárne neseparovateľný príklad prezentovaný na (obr.4(a)). Ak je dvojrozmerný priestor transformovaný do trojrozmerného priestoru (obr.4(b)), čierne vektory a biele vektory sú lineárne separovateľné.

Nech $\Phi$ je transformácia do viacrozmerného priestoru. Transformovaný priestor by mal vyhovovať tej vzdialenosti, ktorá je definovaná v transformovanom priestore a súvisí so vzdialenosťou v pôvodnom priestore. Kernelová funkcia $K (x, \, x')$ , ktorá vyhovuje obom podmienkam, je definovaná nasledovne:

$\displaystyle K (x, \, x') = \Phi (x) ^T \Phi (x')$

(10)

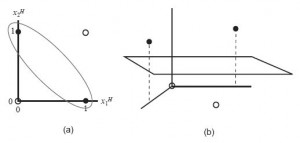
Obr. 4 Lineárne neseparovateľný vektorový priestor (a), Lineárne separovateľný vektorový priestor (b)

Táto rovnosť indikuje, že kernelová funkcia je ekvivalentom vzdialenosti medzi $x$ a $x'$ meranou vo viacrozmernom priestore, transformovaná pomocou $\Phi$ . Ak meriame mierkou podľa kernelovej funkcie a vykonáme optimalizáciu, tak získame nelineárnu hranicu.

Hranicu v transformovanom priestore získame:

$\displaystyle w ^T \Phi (x) + b = 0$

(11)

Potom môžeme vyjadriť:

$\displaystyle \sum _{i} \alpha _i y _i \Phi (x ^T _i) \Phi (x) + b = \sum _i \alpha _i y _i K (x_i, \, x) + b = 0$

(12)

Optimalizačná funkcia v transformovanom priestore sa získava aj nahradením $x_i ^T , \, x_j$ na $K (x _i , x _j )$ . Tieto výsledky dokazujú, že všetky výpočty môžeme získať iba použitím $K (x _i , x _j )$ a nemusíme vedieť presné vyjadrenie $\Phi$ a transformovaného priestoru. Vhodnou podmienkou pre dosiahnutie vzťahu (10) je, že K je kladne definované.
Poznáme niekoľko prípadov kernelovej funkcie:

polynomický kernel

$\displaystyle K (x, \, x') = (x ^T x' + 1 )^p$

(13)

gaussovský kernel

$\displaystyle K (x, \, x') = exp \Bigg (- \frac{\parallel x - x' \parallel ^2}{\sigma ^2} \Bigg )$

(14)

6. Databáza tvárí MIT

Pre našu prácu vstupné signály predstavujú databázu ľudských tvárí, používanú na MIT (Massachusetts Institute of Technology) [http://web.mit.edu/], ktorá pozostáva zo 16 subjektov. Títo ľudia sú zobrazení na (obr. 5). Obraz každého subjektu má rozmery 16×15, 32×30 a 64×60 obrazových prvkov a obsahuje 256 úrovní šedej. Rôzne vzory patriace do tej istej triedy sú na (obr. 6), každý subjekt je zosnímaný s rôznymi náklonmi hlavy, s rôznym osvetlením a rôznymi vzdialenosťami od kamery, spolu 27 vzorov v jednej triede.

Obr. 5 Subjekty pre databázu tvárí

Obr. 6 Rôzne príklady toho istého subjektu

7. Simulácie metód MLP, RBF a SVM

7.1. Popis simulácií

Ako prostredie pre simulácie s metódami MLP a RBF nám poslúžil program Matlab. Software, ktorý sme používali pri metóde SVM je voľne stiahnuteľný program, libsvm-2.85 [13]. Pri všetkých troch metódach sme používali rovnakú trénovaciu a testovaciu množinu pre korektné porovnanie týchto metód.

MLP

Hlavnou úlohou pri viacvrstvovom perceptróne bolo nájdenie vhodného parametra rýchlosti učenia $\eta$ η (v programe Matlab – $l r$ ). V každej simulácií sme zvolili začiatočné parametre siete (okrem spomínaného parametra lr aj spôsob trénovania – napr. traingd, traingdx…), ktoré sme postupne menili tak, aby výsledky testov boli čo najpriaznivejšie.

RBF

V simuláciách s RBF sieťou sme sa snažili nájsť vhodný parameter rozptylu gaussovskej krivky $\sigma$ . V Matlabe bol tento parameter označovaný ako spread constant – SC. Používali sme Matlabovskú funkciu newrb. Tá vytvára sieť postupným pridávaním neurónu, pokiaľ nie je dosiahnuté jej maximum a ten si pre RBF sieť Matlab zvolí automaticky. Závisí od počtu tvárí v trénovacej množine.

SVM

Pre samotný proces trénovania, testu a hľadania najvhodnejších parametrov sme zvolili postup podľa [13] :

transformácia vstupných dát do formátu pre SVM software
nájdenie správnej mierky pre transformované vstupné dáta, tzv. scaling
použitie vhodnej kernelovej funkcie
pomocou programovej funkcie grid.py nájsť najlepšiu hodnotu parametrov
aplikovať nájdené parametre na proces tréningu
testovanie

7.2. Zhodnotenie výsledkov simulácií

Metóda RBF sa prejavila pre rozmery obrazov 16×15 a 32×30 ako vhodným prostriedkom pre verifikáciu ľudskej tváre v obraze. Pre rozmery obrazov 64×60 sme narazili na obmedzenia v prostredí programu Matlab, ktorý nám neumožnil pridávať ľubovoľný počet neurónov do skrytej vrstvy siete, ale určil maximum počtu neurónov z počtu subjektov v trénovacej množine.

V metóde MLP je dôležitým prvkom vhodná topológia siete, ako aj spôsob trénovania. Pre obrazy veľkosti 16×15 a 32×30 sa najlepšie prejavil spôsob trénovania traingd a pre rozmery obrazov 64×60 traingdx.

Pri metóde SVM je nosným prvkom pre úspešnosť testu voľba vhodnej kernelovej funkcie. Pre simulácie, kde trénovaciu množinu tvorila skupina obrazov a11+112+113 o rozmeroch 16×15 to bola polynomiálna funkcia, pričom rovnaké výsledky sa nám podarilo dosiahnuť aj sigmoidálnou funkciou. Pre ostatné trénovacie množiny veľkostí obrazov 16×15, 32×30 a 64×60 sa ako kernelová funkcia najlepšie javila radiálna bázová funkcia.

Výsledky simulácií jednotlivých metód sú znázornené v (Tab. 2) a graficky na (obr. 7). Najúspešnejšou metódou pre obrazy 16×15 a 32×30 je metóda RBF siete, čo pravdepodobne vyplýva z jej lokálnej reprezentácie vstupných dát. Pri väčších rozmeroch uspela metóda SVM. Táto metóda sa prejavila ako najspoľahlivejšia, nakoľko metóda MLP vykazovala v opakovaných testoch pri použití tých istých parametrov nestále výsledky (čo je dôsledkom náhodnej inicializácie váh MLP).

Tab.2. Porovnanie výsledkov pre 16×15, 32×30, 64×60

	Trénovacia množina	Testovacia množina	Test [%]	Úspešnosť
RBF
16×15	a11	ostatne (384 obrazov)	68,4895	263/384
16×15	a11+112+113	ostatne (352 obrazov)	90,909	320/352
32×30	a11	ostatne (384 obrazov)	62,239	239/384
32×30	a11+112+113	ostatne (352 obrazov)	94,602	333/352
MLP
16×15	a11	ostatne (384 obrazov)	45,8333	176/384
16×15	a11+112+113	ostatne (352 obrazov)	75,8523	267/352
32×30	a11	ostatne (384 obrazov)	54,9479	211/384
32×30	a11+112+113	ostatne (352 obrazov)	76,9886	271/352
64×60	a11	ostatne (384 obrazov)	60,6771	233/384
64×60	a11+112+113	ostatne (352 obrazov)	78,6932	277/352
SVM
16×15	a11	ostatne (384 obrazov)	55,4688	213/384
16×15	a11+112+113	ostatne (352 obrazov)	88,9205	313/352
32×30	a11	ostatne (384 obrazov)	57,8125	222/384
32×30	a11+112+113	ostatne (352 obrazov)	89,4886	315/352
64×60	a11	ostatne (384 obrazov)	58,0729	223/384
64×60	a11+112+113	ostatne (352 obrazov)	90,3409	318/352

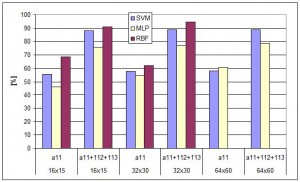
Obr.7 Grafické porovnanie simulácií

7. Odkazy na literatúru

JAIN, A. K. – ROSS, A. – PRABHAKAR, A.: An Introduction to Biometric Recognition. Appeared in IEEE Transactions on Circuits and Systems for Video Technology, Special Issue on Image- and Video-Based Biometrics, Vol. 14, No. 1, January 2004.
CLYDE Wayne Crews Jr., Human Bar Code: Monitoring Biometric Technologies in a
Free Society, Cato Policy Analysis, No. 452 , 2002 Dostupné na internete: http://www.cato.org/pubs/pas/pa-452es.html.
Biometria, http://sk.wikipedia.org/wiki/Biometria
SCHÖN, Otakar: Biometrické technologie razantně nastupují do života. In: Computerworld. číslo vydania 11, 2003, Dostupné na internete:
http://archiv.computerworld.cz/cwarchiv.nsf/clanky/C49A481ED1FFABFDC1256D2E00567197?OpenDocument.
JAIN, A. K. (28-30 April 2004), “Biometric recognition:how do I know who you are?”, Signal Processing and Communications Applications Conference, 2004.
ORAVEC, M. – POLEC, J. – MARCHEVSKÝ, S.: Neurónové siete pre číslicové spracovanie signálov. Bratislava, 1998
POWELL, MJ.D.: The theory of radial basis function approximation in 1990 volume II. Oxford: Clarendon Press, 1992.
KVASNIČKA, V. – BEŇUŠKOVÁ, Ľ. – POSPÍCHAL, J. – FARKAŠ, I. – TIŇO, P. – KRÁĽ, A.: Úvod do teórie neurónových sietí. IRIS, 1997, Dostupné na internete: http://www2.fiit.stuba.sk/~cernans/nn/detailes.html.
MOODY, J. – DARKEN, C.: Fast Learning in Networks of locally-tuned ProcessingUnits, Neural Computation 1. 1989,s. 281-294.
BROOMHEAD, D.S. – LOWE, D.: Multivariate functional interpolation and adaptive networks, Complex Systems, 2. 1988,321-355.
ASANO, A.: Pattern Information Processing. Podklady na predášky: Session 12 (05. 1. 21), Osaka.
MÜLLER, Klaus-Robert – MIKA, Sebastian – RÄTSCH, Gunnar – TSUDA, Koji – SCHÖLKOPF, Bernhard: An Introduction to Kernel-Based Learning Algorithms. IEEE Transactions on Neural Networks, Vol. 12, No. 2, March 2001.
Chih Wei Hsu – Chih Chung Chang – Chih Jen Lin: A Practical Guide to Support Vector Classification. National Taiwan University Taipei 106, Taiwan.

Spoluautormi tohto článku sú:
Matej Féder, Katedra telekomunikácií, Fakulta elektrotechniky a informatiky STU v Bratislave
Miloš Oravec, Katedra aplikovanej informatiky a výpočtovej techniky, Fakulta elektrotechniky a informatiky STU v Bratislave

O časopise

Meta

RSS

Biometrické metódy pre rozpoznávanie obrazov ľudských tvárí

Napísať príspevok

Rubriky

Burza práce

Štúdijné materiály

Archív