Ako ďaleko sú hviezdy – príbeh Tycha de Brahe a Johannesa Keplera
19. Máj, 2010, Autor článku: Balázsová Csilla, Prírodné vedy, Študentské práce
Ročník 3, číslo 5  Pridať príspevok
Pridať príspevok
 Táto práca porovnáva prístup Johannesa Keplera a Tycha de Brahe. Chce čitateľa oboznámiť s planetárnymi modelmi. Chce poukázať na to, akým prínosom boli Brahe a Kepler pre fyziku, ako pomohli Newtonovi založiť dynamiku. Práca skúma, prečo vymyslel Brahe svoj planetárny model. Ďalej pojednáva o tom, ako Kepler zdokonalil heliocentrickú teóriu, ako objavil svoje zákony. Cieľom tejto práce je dokázať súvislosť medzi Keplerovými a Newtonovými zákonmi. Preto na konci sú uvedené dôkazy Keplerových zákonov.
Táto práca porovnáva prístup Johannesa Keplera a Tycha de Brahe. Chce čitateľa oboznámiť s planetárnymi modelmi. Chce poukázať na to, akým prínosom boli Brahe a Kepler pre fyziku, ako pomohli Newtonovi založiť dynamiku. Práca skúma, prečo vymyslel Brahe svoj planetárny model. Ďalej pojednáva o tom, ako Kepler zdokonalil heliocentrickú teóriu, ako objavil svoje zákony. Cieľom tejto práce je dokázať súvislosť medzi Keplerovými a Newtonovými zákonmi. Preto na konci sú uvedené dôkazy Keplerových zákonov.
1. Úvod – základné pojmy
Pozorovateľská astronómia je súčasťou astronómie a zaoberá sa pozorovaním nebeských telies a získavaním údajov o nebeských telesách. Nebeská mechanika skúma kozmické objekty metódami klasickej mechaniky a zaoberá sa výpočtami ich dráh. Hviezdna paralaxa je uhlový posun hviezdy na oblohe pri pozorovaní z dvoch odlišných stanovíšť. Meranie ročnej paralaxy je základná metóda na určovanie vzdialeností hviezd. Ak chceme zmerať ročnú paralaxu, musíme danú hviezdu pozorovať v dvoch ročných obdobiach, a to vtedy, keď sa Zem nachádza v opačných bodoch svojej dráhy – napríklad v marci a v septembri. Dennou paralaxou nazývame uhol, ktorý bol nameraný z dvoch protiľahlých strán Zeme.
Epicyklus je kružnica, po obvode ktorej obieha planéta podľa geocentrického modelu. Stred kružnice sa pohybuje po deferente. Deferent je kružnica, na ktorej sa pohybuje stred epicyklov. Apohéliom nazývame najväčšiu vzdialenosť planéty od Slnka, perihéliom nazývame najmenšiu vzdialenosť planéty od Slnka.
2. Geocentrický planetárny model
Podľa tejto teórie v strede vesmíru sa nachádza nehybná Zem, Slnko a všetky planéty obiehajú okolo nej na dokonalých kruhových dráhach. Tento planetárny model vymysleli v starovekom Grécku. Geocentrickú predstavu, že Zem je stredom celého vesmíru ako prvý sformuloval Anaximandros. Geocentrická predstava sveta sa potom formovala postupne, zdokonalil ju Klaudios Ptolemaios z Alexandrie. Podľa Ptolemaia je Zem v strede vesmíru preto, lebo polovica hviezd, ktorú vidíme, sa nachádza vždy nad horizontom a polovica hviezd pod horizontom. Ďalej predpokladal, že všetky hviezdy sú v rovnakej neveľkej vzdialenosti od stredu vesmíru. Ak by bola Zem bližšie k jednému okraju vesmíru, tak množstvo videných a nevidených hviezd by nebolo rovnaké.
Podľa tohto modelu sa všetky nebeské objekty pohybujú po dokonalých kruhových dráhach. V tomto systéme je každá planéta hýbaná piatimi alebo viacerými krištáľovými sférami. Planéta je ukotvená na rotujúcej sfére epicyklu, a sféra epicyklu je umiestnená na rotujúcej sfére deferentu, pričom epicyklus rotuje v rámci deferentu a deferent rotuje okolo Zeme. Pretože stredy epicyklov Venuše a Merkúra sú vždy na spojnici Zeme a Slnka, to vysvetľuje, prečo vidíme Venušu a Merkúr vždy pri Slnku. V tomto modeli sa planéta pohybuje raz bližšie, inokedy ďalej od Zeme, a pohybuje sa aj dozadu. Tento retrográdny pohyb však nebol dostatočne vysvetlený, preto Ptolemaios vymyslel ekvant.
Ekvant je bod blízko stredu dráhy planéty. Z miesta ekvantu sa stred epicyklu planéty pohybuje s konštantnou rýchlosťou, ale planéta sa na epicykle pohybuje rôznou rýchlosťou. Výsledný model je z nášho pohľadu veľmi nepraktický, lebo každá planéta vyžaduje epicyklus obiehajúci po deferente, odsadený z centra o ekvant, pričom ekvant je iný pre každú planétu. Pôvodný Ptolemaiov model našej slnečnej sústavy obsahuje 40 epicyklov, v zdokonalenom modeli je 80 epicyklov.
3. Heliocentrický planetárny model
Podľa tohto planetárneho modelu v strede vesmíru a v strede Slnečnej sústavy je Slnko, a všetky planéty obiehajú okolo Slnka . Túto teóriu sformuloval Mikuláš Kopernik, ale zdokonalil ju až Johannes Kepler. Podľa pôvodnej teórie planéty obiehajú po dokonalých kruhových dráhach. Stredy týchto kružníc sú mierne excentricky položené vzhľadom na stred Slnka. Stredy excentrických kruhových dráh planét vykonávajú okolo stredu Slnka epicyklické pohyby.
Kopernik v heliocentrickej sústave ponechal 48 epicyklov, totiž pomocou epicyklov vysvetľoval pozorovaný nerovnomerný pohyb planét. Epicykly z heliocentrickej teórie odstránil až Kepler, kto zároveň dokázal, že planéty v skutočnosti obiehajú po eliptických dráhach.
4. Planetárny model Tycha de Brahe
Je akýmsi kompromisom medzi geocentrickým a heliocentrickým planetárnym modelom. V strede vesmíru sa nachádza nehybná Zem, Slnko a Mesiac obiehajú okolo Zeme, ale všetky ostatné planéty obiehajú okolo Slnka. Aj v tomto modeli sú planéty hýbané krištáľovými sférami, a obiehajú po dokonalých kruhových dráhach. Pomocou Tychonickej teórie bolo možné vysvetliť rôzne pozorované odlišnosti vo fázach Venuše, na ktoré Ptolemaiov model nemal vysvetlenie.

Obr.1. Planetárny model Tycha de Brahe
5. Prečo vymyslel Brahe svoju teóriu ?
Hoci Tycho de Brahe uskutočnil najpresnejšie pozorovania hviezd vo svojej dobe, a to dokonca bez ďalekohladu, nedokázal namerať ročnú paralaxu žiadnej hviezdy. Paralaxu Marsu však dokázal namerať. Pritom namerať paralaxu hviezdy Brahovými prístrojmi bolo absolútne nemožné. Hviezdnu paralaxu prvýkrát namerali až v devätnástom storočí. V roku 1837 Wilhelm Struve nameral paralaxu hviezdy alfa Lyr, ktorá sa nachádza v súhvezdí Vega. Paralaxa tejto hviezdy je 0,129″. Naša najbližšia hviezda Proxima Centauri je od nás vzdialená na 4,26 svetelných rokov a má paralaxu 0,762″. Tieto sotva merateľné paralaxy bolo Brahovými prístrojmi nemožné namerať. Brahe dlho uvažoval nad tým, prečo nedokáže zistiť zdanlivý paralaktický pohyb žiadnej hviezdy na oblohe.
Paralaxu hviezd je nemožné namerať, teda Zem sa nepohybuje okolo Slnka, lebo keby sa Zem pohybovala okolo Slnka, tak paralaxy hviezd by sa mali prejaviť. Ďalej z jeho pozorovaní vyplývalo, že ak by sa Zem skutočne pohybovala, potom by hviezdy museli byť od Zeme až tisícnásobne vzdialenejšie ako Slnko. Takéto veľké vzdialenosti hviezd od Zeme však Brahe odmietol. Nakoniec dospel k záveru, že heliocentrické a geocentrické planetárne modely sú nesprávne a vymyslel svoj vlastný planetárny model.
6. Ako pomohol Brahe Keplerovi
V roku 1588 zomrel dánsky panovník Frederik II. Nový panovník však pre Brahovu vedeckú činnosť nemal pochopenie, tak Tycho de Brahe nakoniec opustil Dánsko. Nový domov našiel v Čechách, kam prišiel na pozvanie Rudolfa II. Rudolf II ho vymenoval za cisárskeho matematika. Tycho de Brahe vo svojom kaštieli v Benátkach nad Jizerou vybudoval astronomické observatórium. V roku 1600 Tycho de Brahe pozval Keplera do svojho kaštieľa v Benátkach nad Jizerou.
Kepler potom rok bol Brahovým asistentom a dostal za úlohu určiť dráhu Marsu. Keď Tycho de Brahe náhle zomrel v roku 1601, tak Kepler sa stal Brahovým nasledovníkom na dvore Rudolfa II. Johannes Kepler od pozostalých vysúdil Brahove poznámky a na základe dôkladnej analýzy Brahových pozorovaní objavil svoje zákony.
6.1. Prvý Keplerov zákon
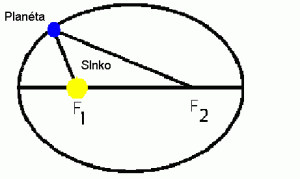
Planéty obiehajú okolo Slnka po eliptických dráhach s malou výstrednosťou, pričom Slnko leží v spoločnom ohnisku týchto elíps. Planéta a Slnko obiehajú okolo spoločného ťažiska. Vo výpočtoch však túto skutočnosť vzhľadom na malú hmotmosť planét v porovnaní s hmotnosťou Slnka zanedbávame. Prvý Keplerov zákon platí aj pre pohyb Mesiaca a umelých družíc okolo Zeme. Vzhľadom na to, že hmotnosť Mesiaca je iba 81-krát menšia ako hmotnosť Zeme, musíme vziať do úvahy ich pohyb okolo spoločného ťažiska.
Matematická formulácia prvého Keplerovho zákona znie:
| (1) |
kde r, θ – sú polárne koordináty, ε – je excentricita elipsy a p je sprievodič. Excentricita je definovaná vzťahom:
| (2) |
kde a, b sú dĺžky hlavnej a vedľajšej polosi elipsy.
6.2. Druhý Keplerov zákon
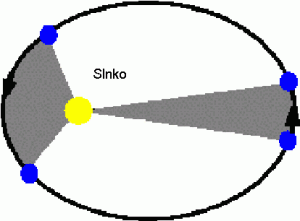
Druhý Keplerov zákon vyjadruje zákon zachovania momentov hybnosti planét. Podľa tohto zákona plošná rýchlosť planéty je konštantná. Veľkosť plochy vytvorenej sprievodičom planéty nezávisí od toho, kde presne sa planéta nachádza.
Keď je planéta k Slnku bližšie, pohybuje sa rýchlejšie, naopak, keď je ďaleko od Slnka, pohybuje sa pomalšie. Plošnú rýchlosť planéty definujeme vzťahom:
| (3) |
kde r je polohový vektor planéty vzhľadom na Slnko, v je okamžitá rýchlosť planéty. Akú veľkú plochu vytvorí sprievodič za interval Δt?
| (4) |
kde v je rýchlosť pohybujúceho sa konca sprievodiča, r je vzdialenosť medzi planétou a Slnkom, α je uhol medzi polohovým vektorom planéty a vektorom jej rýchlosti. Potom veľkosť plošnej rýchlosti môžeme vyjadriť nasledovne:
| (5) |
Výsledkom je veľkosť vektorového súčinu, teda veľkosť vektora plošnej rýchlosti. Skutočne sa zachovávajú momenty hybnosti planét? Namiesto planéty si vezmime časticu. Keď táto častica s hmotnosťou m sa pohybuje rýchlosťou v, tak jej moment hybnosti vzhľadom na jedno z ohnísk elipsy je:
| (6) |
Potom veľkosť momentu hybnosti bude:
| (7) |
Ak zderivujeme tento vzťah podľa času, tak výsledkom bude:
| (8) |
Prvý člen tohto výrazu sa rovná nule, pretože vektory v a mv sú rovnobežné. Aj druhý člen sa bude rovnať nule, totiž jediná sila, ktorá pôsobí na časticu, má opačný smer ako polohový vektor. Z tohto potom vyplýva, že pri pohybe častice sa jej moment hybnosti nemení.
6.3. Keplerov tretí zákon
Pomer druhej mocniny obežnej doby a tretej mocniny dĺžky hlavnej polosi je pre všetky planéty rovnaký. Potom platia nasledujúce vzťahy:
| (9) |
kde k je konštanta úmernosti, T je obežná doba planéty, a a je hlavná polos.
| (10) |
Z týchto vzťahov potom vyplýva, že planéty, ktoré sú vzdialenejšie od Slnka, majú väčšiu obežnú dobu. Obežná doba Saturna je 29,5 pozemských rokov, pričom obežná doba Marsu je iba 1,88 pozemského roka. Ak dráhu planéty budeme považovať za približne kruhovú, tak pomocou obežnej doby T a polomeru R dráhy planéty je možné vypočítať dostredivé zrýchlenie planéty:
| (11) |
Úpravou tohto vzťahu pomocou Keplerovho zákona získame:
| (12) |
Tento výsledok znamená, že sila, ktorou pôsobí Slnko na planétu, sa zmenšuje s druhou mocninou vzdialenosti planéty od Slnka.
7. Ako inšpiroval Kepler Newtona
Isaac Newton sa narodil 60 rokov po Keplerovej smrti. Newton objavil pohybové zákony, gravitačný zákon, zaviedol pojem gravitácia. V roku 1687 publikoval Matematické Princípy Prírodnej Filozofie. Tu uviedol pohybové zákony, teóriu gravitácie, gravitačný zákon, a poukázal na súvislosť medzi Keplerovými planetárnymi zákonmi a svojou teóriou gravitácie. Takto dokázal správnosť heliocentrickej teórie. Pomocou jeho nových teórií a zákonov už bolo možné vysvetliť, čo spôsobuje príliv a odliv. Zmeny v hladinách oceánov sú spôsobené gravitačným vplyvom Mesiaca, keď obieha okolo Zeme.
7.1. Newtonove pohybové zákony
Zákon zotrvačnosti znie: Jestvuje súradnicová sústava, vzhľadom na ktorú teleso zotrváva v pokoji, alebo priamočiarom rovnomernom pohybe, ak nepodlieha vplyvu iných telies. Inerciálna sústava je taká súradnicová sústava, kde platí zákon zotrvačnosti. Formulácia zákona sily: Zrýchlenie a telesa je úmerné pôsobiacej sile F a nepriamo úmerné jeho hmotnosti m.
| (13) |
V tomto vzťahu vystupujú sila, hmotnosť, a konštanta ktorej hodnota závisí od voľby jednotiek sily, hmotnosti a zrýchlenia. Silu je možné definovať aj na základe zrýchlenia, ktoré udelí telesu. Podiel veľkostí dvoch síl F a F1 sa rovná podielu zrýchlení a, a1 ktoré tieto sily udelia tomu istému telesu:
| (14) |
Hmotnosť je veličina, ktorá vyjadruje zotrvačné vlastnosti telies. Ak na urýchlenie dvoch telies použijeme rovnakú silu, tak zrýchlenie ťažšieho telesa je menšie. Hmotnosti týchto telies označíme m a m2. Hmotnosť ľahšieho telesa je m, hmotnosť ťažšieho telesa je m2. Sila F udeľuje telesu s hmotnosťou m zrýchlenie a, telesu s hmotnosťou m2 zrýchlenie a2. Sila F1 udeľuje telesu m zrýchlenie a1, telesu m2 zrýchlenie a21. Potom hmotnosť definujeme pomocou nepriamej úmernosti:
| (15) |
Ak z tejto úmery vyjadríme a1, a dosadíme do predchádzajúcej úmery, tak dostaneme:
| (16) |
Nasledujúci výraz predstavuje konštantu k zo zákona sily (13):
| (17) |
Zvoľme jednotkovú silu F1 tak, aby telesu s jednotkovou hmotnosťou udeľovala jednotkové zrýchlenie. V tomto prípade konštantanta k sa stane bezrozmernou, bude mať hodnotu 1 a potom zákon sily nadobudne tvar:
| (18) |
Tretí Newtonov pohybový zákon znie: Ak na seba pôsobia dve telesá, tak na seba pôsobia rovnakými silami opačného smeru, pričom pôsobia v jednej priamke.
| (19) |
Ak silu pôsobiacu na jedno teleso nazývame akcia, tak silu, ktorá má opačný smer a pôsobí na druhé teleso, nazývame reakcia.
7.2. Newtonov gravitačný zákon
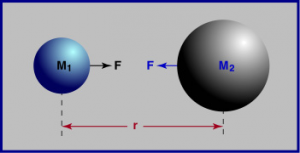
Každé teleso pôsobí na ostatné telesá gravitačnou silou. Gravitačná sila ťahá všetky ostatné telesá smerom k stredu daného telesa. Veľkosť gravitačnej sily závisí od hmotnosti telesa. Slnko má väčšie gravitačné pôsobenie ako Zem, a gravitácia na Zemi je asi šesťkrát väčšia ako na Mesiaci. Matematická formulácia gravitačného zákona je:
| (20) |
kde FG je gravitačná sila, je gravitačná konštanta, m1 je hmotnosť prvého telesa, m2 je hmotnosť druhého telesa a r12 je vzdialenosť medzi nimi. S ohľadom na vektorový charakter sily možno tento vzťah napísať aj takto:
| (21) |
Záporné znamienko vyjadruje skutočnosť, že sila FG , ktorá pôsobí na jedno teleso má opačný smer ako polohový vektor r, ktorého začiatok sa umiestňuje do stredu druhého telesa.
8. Dôkazy Keplerových zákonov
8.1. Dôkaz prvého Keplerovho zákona z Newtonovskej dynamiky
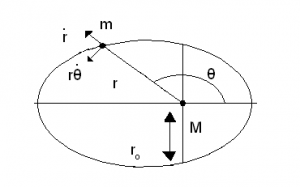
Obr. 5. K dôkazu prvého Keplerovho zákona
Nech malé teleso s hmotnosťou m obieha na eliptickej dráhe okolo väčšieho telesa M. Celková energia tohto systému je :
| (22) |
kde r je najväčšia vzdialenosť medzi m a M,v je rýchlosť telesa m, κ je gravitačná konštanta. Zavedieme označenia derivácií:
| (23) |
| (24) |
Prepíšme rovnicu (22) pomocou polárnych súradníc:
| (25) |
Moment hybnosti telesa m bude:
| (26) |
Zaveďme subsitúciu:
potom
| (27) |
Zintegrujme to:
| (28) |
Teraz bude:
| (29) |
Potom výsledok bude:
| (30) |
Úpravou rovnice (22), a vyjadrením dostaneme:
| (31) |
Zavedieme substitúcie:
| (32) |
| (33) |
Ak upravíme rovnicu (31), tak dostaneme:
| (34) |
Vyjadrenú dosadíme do rovnice (30), a po úpravách dostaneme:
| (35) |
| (36) |
Ak túto rovnicu upravíme, tak dostaneme rovnicu elipsy v polárnych koordinátach:
| (37) |
kde r0 je sprievodič, a e je excentricita.
8.2. Newtonov dôkaz druhého Keplerovho zákona
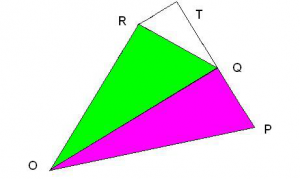
Obr. 6. K dôkazu druhého Keplerovho zákona
Veľkosť plochy, ktorú vytvorí sprievodič planéty, je rovnaká v rovnakých časových intervaloch. Predpokladajme, že častica sa pohybuje z bodu P do bodu Q a do bodu R v rovnakých časových intervaloch. Častica je poháňaná silou, ktorá smeruje do bodu O, potom zrýchlenie v bode Q je vo smere QO. Zvoľme jednotku času tak, aby PQ predstavoval rýchlosť z P do Q. Potom QR predstavuje rýchlosť z Q do R. Vektory QT a PQ nech sú rovnaké. Potom trojuholník QTR je vektorový trojuholník, kde rýchlosti a zrýchlenia sú definované z bodu Q. TR predstavuje zrýchlenie. Vektor TR je rovnobežný s vektorom QO.
| (38) |
Plochy trojuholníkov PQO, QTO, QRO sú rovnaké, lebo QT a PQ sú rovnaké, a trojuholníky PQO a QTO majú rovnakú výšku. Keďže trojuholník QRO je rovnostranný, tak trojuholník QRO má rovnakú plochu ako ostatné dva trojuholníky. To znamená, že za rovnaký časový interval častica prejde rovnaké plochy, a to sme chceli dokázať.
9. Odkazy na literatúru
- Fergusonová, K.: Tycho a Kepler. Nesourodá dvojice, jež jednou provždy změnila náš pohled na vesmír. Praha, Academia, 2009, pp. 19 – 386. ISBN 978-80-200-1713-0
- Ballo, P.: Ako ďaleko sú hviezdy [online]
http://kf.elf.stuba.sk/~ballo/vesmir/meranie-p.ppt - Wikipedia. Johannes Kepler [online]
http://sk.wikipedia.org/wiki/Johannes_Kepler - Wikipedia. Tycho Brahe [online]
http://sk.wikipedia.org/wiki/Tycho_Brahe - Wikipedia. Tycho Brahe [online]
http://en.wikipedia.org/wiki/Tycho_Brahe - Wikipedia. Johannes Kepler [online]
http://en.wikipedia.org/wiki/Johannes_Kepler - Wikipedia. Isaac Newton [online]
http://en.wikipedia.org/wiki/Isaac_Newton - Červeň, I.: Fyzika po kapitolách, časť 5. Gravitačné pole, Hydromechanika. Bratislava,Vydavateľstvo STU, 2007, pp. 2 -7. ISBN-978-80-227-2667-2
- Červeň, I.: Fyzika po kapitolách, časť 3. Dynamika hmotného bodu. Bratislava, Vydavateľstvo STU, 2007, pp. 2 – 4. ISBN-978-80-27-2665-8
- Teórie – geocentrizmus, heliocentrizmus, Newtonove zákony. [online]
http://www.ovesmire.webzdarma.cz/teorie/teorie-zakladne.html - Keplerove zákony. [online]
http://www.gravitywarpdrive.com/NGFT_Chapter_5.htm - Proof of Kepler’s first law from Newtonian dynamics. [online]. http://radio.astro.gla.ac.uk/a1dynamics/ellproof.pdf
- Newton’ s proof of Kepler ‘s second law [online].
http://www.arbelos.co.uk/Papers/Newton-Kepler.pdf - Wikipedia. Stellar parallax. [online]
http://en.wikipedia.org/wiki/Parallax#Stellar_parallax - Meranie vesmírnych vzdialeností. [online]
http://astroportal.sk/technika/meranie_vzdialenosti.html - Astronomický heslár – zoznam hesiel.[online]
http://www.ta3.sk/~zkanuch/apvv/wwwheslar/ - Britannica Online Encyclopedia. Brahe, Tycho: model of planetary motion. [online]
http://www.britannica.com/EBchecked/topic-art/77001/2723/Engraving-of-Tycho-Brahes-model-of-the-motion-of-the
Spoluautorom článku je prof. Ing. Peter Ballo, PhD., Katedra fyziky, Fakulta elektrotechniky a informatiky, Slovenská technická univerzita, Ilkovičova 3, 812 19 Bratislava