Opis rýchlostného poľa partikulárnych látok v kónickej násypke
28. Jún, 2010, Autor článku: Krok Alexander, MATLAB/Comsol, Strojárstvo
Ročník 3, číslo 6  Pridať príspevok
Pridať príspevok
 Základné predpoklady správania sa partikulárnych materiálov zaviedol Johanson a Jenike (1962) a ich poznatky využilo mnoho vedeckých pracovníkov v ich teoretických a experimentálnych prácach. S vývojom nových experimentálnych techník dodnes vznikajú vedecké práce v ktorých autori ponúkajú najrôznejšie prístupy a metódy, ktorými možno správanie sa takýchto materiálov opísať.
Základné predpoklady správania sa partikulárnych materiálov zaviedol Johanson a Jenike (1962) a ich poznatky využilo mnoho vedeckých pracovníkov v ich teoretických a experimentálnych prácach. S vývojom nových experimentálnych techník dodnes vznikajú vedecké práce v ktorých autori ponúkajú najrôznejšie prístupy a metódy, ktorými možno správanie sa takýchto materiálov opísať.
Okrem tradičných meraní veličín, ktoré sledujú statické správanie sa partikulárnych látok(vnútorný uhol trenia , vonkajší uhol trenia
, koeficient stlačiteľnosti K, striasaná a nestriasaná hustota
,
) sa v poslednom desaťročí využívajú i jednoduchšie numerické simulácie na predpoveď dynamických vlastnosti sypkých materiálov. Pri výpočte je potrebné poznať pohyb materiálu a ten je možné zaznamenávať vysokorýchlostnou kamerou. Dôležitou a v súčasnosti stále častejšie využívanou metódou na meranie rýchlostných polí je metóda Particle Image Velocimetry (PIV), ktorá umožňuje získať obraz rýchlostného poľa vo vyšetrovanej rovine v určitom okamihu. Ešte pred samotným meraním fyzikálne komplikovanejších procesov, ako je napríklad valcové stláčanie sypkých materiálov, bola táto metóda odskúšaná pri opise vyprázdňovania materiálu z kónickej násypky.
1. Úvod
Takmer v každom priemyselnom odvetví sa stretávame s použitím a spracovaním látok tuhého skupenstva. Takéto látky môžu byť východiskovou zložkou spracovateľských technológií (ťažobný priemysel, energetika) alebo výsledkom finálnych technológií (chemický, farmaceutický priemysel a pod.). Charakteristickým znakom stavu týchto látok je to, že sú vo väčšine prípadov v jemnodisperznej forme. Z hľadiska manipulácie, spracovania alebo použitia majú jemnozrnné materiály niektoré negatívne vlastnosti. Preto sa snažíme vhodným procesom túto formu materiálu pozmeniť. Jednou z výskumných činnosti Ústavu procesného a fluidného inžinierstva SjF STU je výskum technológii a procesov granulácie a úpravy vlastností práškových materiálov s cieľom prispieť k dokonalejšiemu poznaniu správania sa týchto materiálov.
Základné predpoklady správania sa partikulárnych materiálov zaviedol Johanson a Jenike [3] a ich poznatky využilo mnoho vedeckých pracovníkov v ich teoretických a experimentálnych prácach. S vývojom nových experimentálnych techník dodnes vznikajú nové vedecké práce v ktorých autori ponúkajú najrôznejšie prístupy a metódy, ktorými možno správanie sa takýchto materiálov opísať. Napríklad Spencer a Bradley [7] prezentovali teóriu pre tok granulačných materiálov pod vplyvom gravitačných síl pre axiálne symetrické prúdenie, z ktorej odvodili teoretické vzťahy opis vyvíjajúcej sa rýchlosti v granulovanom materiály vysypávaného z násypky klinového alebo kónického tvaru. Massoudi a Phuoc [6] sledovali účinky medzných šmykových podmienok a Liao, Hsiau a Li a Tai [5] sa zase zaoberali vplyvom gravitácie na dynamické vlastnosti prúdenia tohto materiálu. Kvapil [4] použil materiál dvoch rôznych farieb na určenie prúdiacej a stagnujúcej zóny. Drescher et. al. [1] pomocou stereofotografickej techniky uskutočnil experimenty v rovinnom zužujúcom sa zásobníku a Drescher a Ferjani [2] vytvorili model vývoja prúdiacej zóny nesúdržného granulovaného materiálu a zaviedli upravený kinetický model. Olšiak riešil vybrané problémy výskumu hydraulických zariadení vizualizačnou metódou [9].
Okrem tradičných meraní charakteristík, ktoré sledujú správanie sa partikulárnych látok sa v poslednom desaťročí využívajú i jednoduchšie numerické simulácie pri ktorých sú aplikované komerčné výpočtové programy. Pri stálom zvyšovaní výkonu počítačovej techniky vznikajú tiež nové metódy experimentálneho výskumu umožňujúce štatistické spracovanie veľkého množstva obrazových dát. Dôležitou a v súčasnosti stále častejšie využívanou metódou na meranie rýchlostných polí je metóda Particle Image Velocimetry (PIV), ktorá umožňuje získať obraz rýchlostného poľa vo vyšetrovanej rovine v určitom okamihu. V minulosti boli merania, z ktorých možno získať rýchlostný profil prúdiacej tekutiny, uskutočňované s laserovým dopplerovým anemometrom (LDA). Dobre prevedené merania s LDA poskytujú nielen strednú hodnotu rýchlosti, ale i turbulentné charakteristiky a však v jednom bode. Treba poznamenať, že tieto metódy sa vo väčšine prípadov používajú na meranie rýchlostných polí prúdiacich kvapalín a plynov. Za určitých predpokladov sa dá metóda PIV použiť aj v prípade merania toku partikulárnych látok. V prvom rade si treba ozrejmiť, do akej miery táto metóda poskytne dôveryhodné výsledky. Preto ešte pred samotným meraním fyzikálne komplikovanejších procesov, ako je napríklad valcové stláčanie sypkých materiálov, bola táto metóda odskúšaná pri opise klasického vyprázdňovania materiálu z kónickej násypky. Toto zariadenie bolo zvolené za skúšobné preto, lebo násypka so zúženým dnom je s konštrukčného hľadiska veľmi jednoduché zariadenie a okrem gravitačných účinkov na tento systém nepôsobia iné významné sily. Tento príspevok ponúka zhrnutie skúseností, ktoré boli získané počas merania pri samotnom experimente, ale i ďalšom spracovaní údajov. Keďže je potrebné poznať taktiež rozloženie tlakov v zásobníku, prvá kapitola uvádza jeden zo spôsobov určovania zložiek horizontálneho a vertikálneho napätia.
2. Tlaky partikulárnych látok na steny zásobníka
Od zásobníkov na kvapaliny sa zásobníky na sypké hmoty líšia tým, že tlak v zásobníku narastá lineárne s hrúbkou ako u kvapalín, ale časť váhy sypkého materiálu sa prenáša trením na steny. Hlavným úkolom pri určovaní tlakových pomerov v zásobníku je určenie rozloženia horizontálneho a vertikálneho napätia po výške zásobníka ktoré možno .získať z bilancie síl pôsobiacich na skúmaný systém (obr. 1).

Obr. 1. a) Vektory zložiek napätia b) Stav napätia v sypkom materiály c) Stenové tlaky 1(aktívny stav), 2 (prechodový stav), 3 (pasívny stav) 4 (priebeh pretlakovej vlny)
Vertikálne a horizontálne napätie možno podľa Janssenovej rovnice [10] vyjadriť podľa nasledujúceho vzťahu 1 a 2.
| (1) |
| (2) |
Pri výpočte sa vychádza z úvahy, že napätie na stenách zásobníka sa môže zväčšovať a to v prípade že sa zväčšujú Móhrové kružnice a tento stav je označovaný ako aktívny stav. V prípade že jeho napätie klesá, Móhrové kružnice sa zmenšujú a daný stav sa označuje ako stav pasívny.
Počas vysypávania materiál podlieha tak aktívnemu ako aj pasívnemu stavu a v závislosti od toho sa volí hodnota K, ktorá je potrebná na výpočet zložiek vertikálneho a horizontálneho napätia (vzťah 3 a 4).
| (3) |
| (4) |
Výsledky tejto úvahy je možne vidieť na obrázku 2 a 3, kde vidieť zmenu veľkosti napätia obidvoch zložiek v závislosti od zmeny stenového trenia.

Obr. 2. Horizontálne a vertikálne napätie v závisloti od zmeny
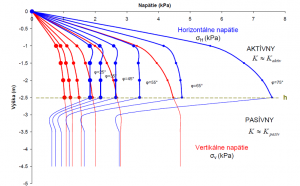
Obr. 3. Horizontálne a vertikálne napätie v závisloti od zmeny
3. Meranie metódou PIV
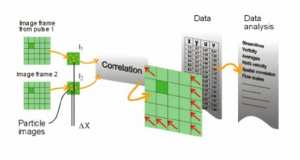
Pomocou PIV systému sa meria rýchlostne pole v tekutine pomocou vysokorýchlostného snímania obrazu. Aby bolo možné stanoviť pohyb častíc v meranom priestore, je potrebné zhotoviť dve snímky s veľmi krátkou periódou. Dve snímky zaznamenané bezprostredne po sebe v časovom intervale sú označené ako dvojica snímok a v ďalšom spracovaní vytvárajú základnú dátovú sadu pre vyhodnotenie rýchlosti prúdenia. Snímky sú rozdelené do obdĺžnikových oblastí, ktoré sa nazývajú vyšetrované oblasti. Pre každú z týchto vyšetrovaných oblastí vytvára obrázok častíc zachytený prvou snímkou a obrázok častíc zachytený druhou snímkou náhradný vektor.
Tento vektor je vypočítaný pomocou cross – korelačnej analýzy. Vzájomná korelácia vyjadruje mieru podobnosti dvoch signálov. Výsledkom cross – korelacie je plocha pikov v korelačnej rovine. Každý peak svojou výškou a plochou voči ostatným určuje s akou štatistickou pravdepodobnosťou došlo v príslušnej vyšetrovanej oblasti k posunutiu častíc, ktoré sú reprezentované vektorom s počiatočným bodom v strede nulového peaku a koncovým v strede každého ďalšieho peaku. Výpočet najpravdepodobnejšieho posunutia sa tak zúži na hľadanie najvyššieho peaku s najpriaznivejšími štatistickými parametrami. Na určenie vzdialenosti obrazu sa používa proces rýchlej Fourierovej transformácie. Namiesto kontinuálnej korelačnej funkcie je k dispozícii konečný počet bodov reprezentujúcich korelačnú rovinu, kde priestor medzi pixelmi zodpovedá priestoru medzi diskrétnymi hodnotami funkcie Fourierovej transformácie. Nakoľko poznáme teoreticky tvar krivky v korelačnej rovine a preložíme túto známu krivku danými diskrétnymi bodmi funkcie Fourierovej transformácie, môžme presnejšie určiť stred značkovacej častice. Ak poznáme presnú polohu stredu každej značkovacej častice vo vyšetrovanej oblasti, môžme určiť vzdialenosť medzi prvým a druhým obrázkom častice s presnosťou menšou ako jeden pixel pitch. Tento proces sa nazýva Subpixelova interpolácia. Potom je vykonaná Fourierova transformácia týchto polí a z dvoch obdŕžaných funkcií vypočítaná vzájomná korelácia s následným výpočtom inverznej Fourierovej transformácie. Týmto je vypočítaný vektor posunutí, ktorý vydelením dĺžkou časového intervalu ∆t medzi zhotovením jednotlivých snímok a vynásobením rozmerovou mierkou pixelov vyjadrí výslednú rýchlosť.
Pri meraní metódou PIV sa používa laserový list, ktorý osvetlí cely prierez meranej plochy. Pôvodnú zostavu PIV bolo potrebné podobne ako to spravil Steingart a Evans [8] potrebné upraviť, pretože bola použitá partikulárna látka a laser, ktorý sa bežne pri tejto metóde používa, by takýto materiál nepresvietil. Aby boli eliminované svetelné odrazy, ktoré počas snímania vznikali a bola dosiahnutá lepšiu viditeľnosť, miesto lasera bola použitá halogénová lampa.
4. Opis experimentu
Počas samotného merania sa bolo treba vysporiadať s nežiadúcimi vplyvmi, ktoré sa vyskytli pred ale aj počas samotného merania. V prvom rade boli identifikované a odstránené základné nežiadúce vplyvy. Bolo treba zabezpečiť, aby násypka bola dostatočne priehľadná a nevznikali rušivé segmenty na snímanom obraze. Preto bolo použité plexisklo o relatívne malej hrúbke. Halogénová lampu bola umiestnená do vhodnej polohy tak, aby boli odstránené odtiene na snímanom obraze, nastavená vhodná frekvenciu snímania a aby bola zabezpečená dostatočná presnosť posuvu materiálu vkrátkom časovom intervale. Experiment bol limitovaný možnosťou regulácie sypania materiálu, preto sa predpokladalo, že výstupný signál nebude čistý. Experimenty opísané v tomto článku boli robené v troch rovinných násypkách vyrobených zplexiskla. Stena každého modelového zariadenia má tvar rovnoramenného trojuholníka s výškou 80 cm. Šírky komory modelu je 10 cm s uhlom sklonu stien k vertikále 45° , 30° a 20°. Dĺžka hornej hrany steny je 104 cm a šírka vypúšťacieho otvoru je 1 cm. Partikulárny materiál sa zbieral do nádoby umiestneného pod výsypným otvorom a bol použitý na ďalšie merania. Vývoj prúdenia sypkého materiálu bol zaznamenávaný vysokorýchlostnou kamerou. Zostava experimentálneho zariadenia získala série po 700 obrázkov, ktoré boli uložené na pevný disk počítača. Po ukončení experimentov boli súbory obsahujúce obrázky použité na určenie rýchlostných polí. Osvetlenie s dvoma halogénovými lampami umožňovalo zhotoviť záznamy prúdenia piesku v násypke bez rušivých tieňov. Časový interval medzi obrázkami bol 0,05 s a ktorý predstavoval optimálnu hodnotu na zachytenie najmenšieho posunutia zŕn piesku počas prúdenia. Meranie posunutia zŕn udáva za časový interval na získanie lokálnych vektorov rýchlostí.
Jednotlivé záznamy boli ďalej spracované v komerčnom programovom balíku Matlab. Modelovým materiálom bol piesok. Vlastnosti tohto materiálu su uvedené v tabuľke 1.
Tabulka 1. – Vlastnosti piesku
| Porozita | Výsypný uhol |
Nestriasaná hmotnosť |
Striasaná hmotnosť |
Hausnerov pomer HR [-] | Uhol vonkaj – šieho trenia |
Uhol vnútor – ného trenia |
|
|---|---|---|---|---|---|---|---|
| Piesok | 0,368 | 20,9 | 1615 | 1907 | 1,18 | 22,1 | 34 |
5. Experimentálne výsledky
Hneď po otvorení vypúšťacieho otvoru sa materiál uviedol do pohybu. V zásade sa jednalo o jadrový tok a materiál sa pohyboval do prúdiacej zóny z hornej časti lavínovým spôsobom. V skutočnosti sa vyformoval prúdiaci kanál v zvislej osi symetrie modelu. V spodnej časti sú hranice prúdenia takmer vertikálne, vo vyšších častiach sa zóna prúdenia rozširuje a nakoniec siaha až k stenám násypky. V zóne prúdenia sú vektory rýchlostí prevažne vertikálne, pozdĺž prúdiaceho kanála.
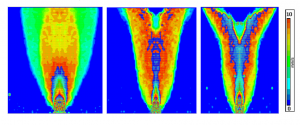
Obr. 5. Rozdelenie vektorov rýchlosti počas vysipávania
Bolo zistené, že sledovaná plocha prúdenia narastá sčasom ašmykové zóny sa vyskytujú medzi prúdiacim a stagnujúcim materiálom v prípade, že ide o neustálený stav, teda bez dosypávania materiálu až do úplného vyprázdnenia násypky (obr. 5). V prípade, že počas merania sa do násypky materiál dosypáva tak, aby bola násypka trvale plná, je možné aspoň približne zabezpečiť podmienky pre ustálený stav. Vtedy sa rýchlostný profil v čase mení minimálne. (obr 6).
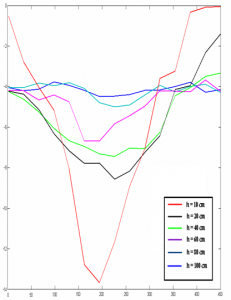
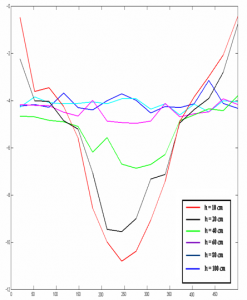

Obr. 6. Vývin rýchlostných profilov v neustálenom stave počas vysypávania
Jedna z možností, ako posúdiť či je daný proces ustálený alebo neustálený, je merať okamžitú rýchlosť v jednom zvolenom bode snímaného obrazu počas celého merania, čo umožní posúdiť zo získaného časového priebehu tendenciu zmeny rýchlosti v čase (obr. 7).
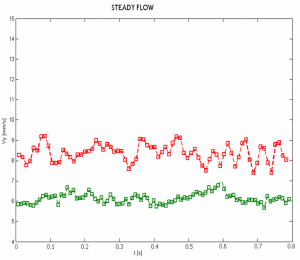

Obr. 7. Časový priebeh vertikálnej rýchlosti vybraného bodu pri ustálenom a neustálenom stave
Pre verifikáciu výsledkov boli uskutočnené experimenty v rúrke štvorcového prierezu s rozmermi 20 x 20 cm a dĺžke 70 cm. Predpokladalo sa, že v takejto rúrke nedochádza pri sypaní partikulárnych látok k vytvoreniu priečnych rýchlostných profilov v závislosti na čase a ani v závislosti od vertikálnej polohy vrstvy. Po otvorení výpustného otvoru sa všetok materiál uviedol do pohybu piestovým tokom. Počas prúdenia partikulárnej látky nevznikla stagnujúca zóna, čo znamená, že sa predpoklad potvrdil. Získané rýchlostné profily je možné vidieť na obrázku 8.
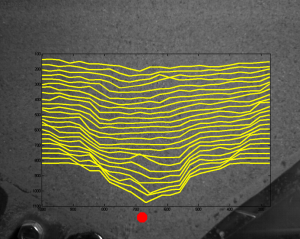

Obr. 8. Provnanie rýchlostného profilu a) pre násypku so sklonom bočných stien 45°, b) pre násypku bez sklonu bočných stien
Pri ďalšom spracovaní údajov je výhodnejšie poznať funkciu ktorá opisuje namerané rýchlostné pole, preto boli namerane údaje podrobené regresnej analýze (obr. 9).

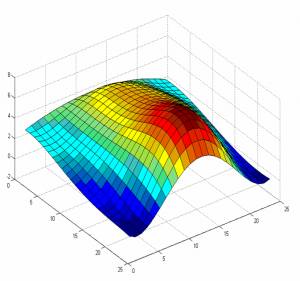
Obr. 9. Provnanie rýchlostného profilu a) získany z nameraných údajov, b) získany z regresnej analýzy
6. Záver
Uvedená metóda je vhodná na určenie rýchlostných profilov prúdiacej partikulárnej látky nielen v násypkách. V blízkej dobe je plánované overiť tento postup na vyhodnotenie rýchlosti prúdenia partikulárnej látky v násypke valcového kompaktora s komplikovaným napätostným systémom. V tomto prípade je proces zložitejší ako pri gravitačnom prúdení, na materiál pôsobí vertikálna sila od núteného plnenia a zaťahujúce sily od otáčajúcich sa valcov. Napriek komplikovanému systému sa však dá predpokladať, že bude možné získať vektorové pole prúdenia častíc v násypke.
7. Zoznam symbolov
| Vertikálne napätie | kPa | |
| Horizontálne napätie | kPa | |
| Striasaná hmotnosť | kg.m-3 | |
| Nestriasaná hmotnosť | kg.m-3 | |
| Uhol vonkajšieho trenia | ° | |
| Uhol vnútorného trenia | ° | |
| g | Tiažové zrýchlenie | m.s-2 |
| D | Hrúbka zásobníka | m |
| K | Koeficient bočného tlaku | - |
| Prítlačné napätieu | kPa | |
| HR | Haussnerov pomer | - |
8. Zoznam použitej literatúry
- Drescher, A., Cousens, T.W., Bransby, P.L., 1978. Kinematics of the mass flow of granular material through a plane hopper. Geotechnique 28, 27.
- Drescher, A., Ferjani, M., 2004. Revised model for plug/funnel flow in bins. Powder Technology 141, 44–54.
- Johanson, J.R., Jenike, A.W.,1962. Stress and velocity fields in gravity flow of bulk solids. University of Utah Engineering Experiment Station, Bulletin, vol. 116, USA
- Kvapil, R., 1959. Theorie der Schuttgutbewegung. VEB Verlag Technik, Berlin
- Liao, C.-C., et al., The influence of gravity on dynamic properties in sheared granular flows. Chemical Engineering Science (2010), doi:10.1016/j.ces.2009.12.034
- Massoudi, M., Phuoc, T.X., 1999 . The e!ect of slip boundary condition on the flow of granular materials: a continuum approach. International Journal of Non- Linear Mechanics 35 (2000) 745}761
- Spencer, A.J.M., Bradley, N.J., 2002 . Gravity flow of granular materials in contracting cylinders and tapered tubes. International Journal of Engineering Science 40 (2002) 1529–1552
- Steingart, D.A., Evans, J.W., 2005. Measurements of granular flows in twodimensional hoppers by particle image velocimetry. Part I: experimental method and results. Chemical Engineering Science 60, 1043–1051.
- Olšiak, R.: Riešenie vybraných problémov výskumu hydraulických strojov metódou vizualizácie. In: Mechanical Engineering 2007 : the 11th International Scientific Conferenc. Bratislava, November 29-30, 2007. – Bratislava : STU v Bratislave, 2007. – ISBN 978-80-227-2768-6.
- Novosad, J.: Mechanika sypkých hmot (skriptum), Vysoká škola chemicko – technologická Praha, Praha 1983
Spoluautor tohto článku je Marián Peciar, Slovenská technická univerzita, Strojnícka fakulta, Námestie slobody 17, 812 31 Bratislava 1.