Bunkové telesá – Penové materiály
III. Vlastnosti bunkových telies

27. September, 2010, Autor článku: Goga Vladimír, Elektrotechnika
Ročník 3, číslo 9 This page as PDF Pridať príspevok

Skúmanie a tvorenie nových materiálov je dôležitou oblasťou pre vylepšenie technológií a výrobkov. V konečnom dôsledku sa hľadajú materiály s výnimočnými vlastnosťami použiteľnými pre prax. V tomto článku sú popísané fyzikálne, chemické, mechanické a absorčné vlastnosti bunových telies.

1. Vlastnosti bunkových telies

Vlastnosti bunkových penových telies sú výsledkom kombinácie vlastností bunkovej štruktúry a vlastností materiálu použitého na jeho výrobu. Tieto dva faktory spolu s relatívnou hustotou bunkových telies sú určujúcimi parametrami pre ich fyzikálne a mechanické vlastnosti (obr. 1).


Obr. 1 Faktory ovplyvňujúce vlastnosti bunkových telies.

Na obr. 2 je znázornené porovnanie štyroch vlastností: hustota, tepelná vodivosť, Youngov modul pružnosti a pevnosť v tlaku plných a bunkových materiálov.


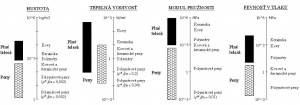
Obr. 2 Porovnanie vlastností penových a plných materiálov [1].

2. Fyzikálne vlastnosti

Hustota (merná hmotnosť):

Nízka hustota, tým pádom aj hmotnosť bunkových telies ja daná bunkovou štruktúrou, obsahom dutín v bunkách je zvyčajne plyn. Dôležitým parametrom pri porovnávaní bunkových telies je ich tzv. relatívna hustota:

\rho_{rel} = \frac{\rho^*}{\rho_S} (1)

Relatívna hustota predstavuje podiel hustoty penového materiálu \rho^* a  hustoty materiálu \rho_S, z ktorého je pena vyrobená. Mieru voľného miesta vyplneného plynom alebo kvapalinou charakterizuje pórovitosť:

\phi = 1 - \frac{\rho^*}{\rho_S} (2)

Obecne možno povedať, že bunkové materiály majú relatívnu hustotu menšiu ako 0,3, ultraľahké peny dokonca až 0,003. Hustota je určujúcim faktorom, ktorý ovplyvňuje ostatné, či už fyzikálne alebo mechanické vlastnosti bunkových telies, preto sa jej zmena využíva na dosiahnutie požadovaných hodnôt vlastností, žiadaných pre danú aplikáciu použitia pien.

Vodivosť (elektrická a tepelná):

Vodivosť bunkových telies, či už elektrická alebo tepelná je vo všeobecnosti nižšia ako pri plných telesách. Dôvodom je nízky podiel materiálu stien a hrán v objeme buniek a vysoký pomer plynových dutín v objeme bunkového telesa. Tým je zrejmé, že vodivosť narastá s nárastom hustoty bunkových telies. Pri kovových penách je ich tepelná vodivosť zhruba 1/10 vodivosti kovu, z ktorého je vyrobená. Ich tepelná vodivosť sa môže ešte znížiť ďalším oxidačným spracovaním. Koeficient tepelnej rozťažnosti kovových pien je rovnaký ako pri plných kovoch.

Zvukovo a vibračno-izolačné vlastnosti:

Zvukové vlny sa v penách odrážajú od ich nepravidelnej štruktúry. Vibračná energia spôsobuje deformáciu stien buniek a mení sa na tepelnú energiu. Preto intenzita odrazeného zvuku klesá. Absorpčný stupeň pohltenia možno zvýšiť jemným a homogénnym rozložením buniek v objeme materiálu.

3. Chemické vlastnosti

Chemickými vlastnosťami vynikajú prevažne kovové peny. Sú nehorľavé, nevylučujú toxické plyny pri ohreve, ale korodujú rovnako ako plné kovy.

4. Mechanické vlastnosti

Podľa pracovných diagramov je správanie sa pien v ťahu a tlaku rozdielne. V tlaku je výrazná tzv. plató oblasť, kde deformácie rozsiahle narastajú pri minimálnej zmene napätia (obr. 3), čím sa zvyšuje ich schopnosť pohlcovať energiu, ktorá sa využíva pri aplikáciách pien ako baliaci, absorbčný a ochranný materiál. V ťahu je táto oblasť veľmi slabo výrazná.


Obr. 3 Pracovný diagram pien ŤAH – TLAK.

Na obr. 4 je znázornený typický pracovný diagram pien pri tlakovom zaťažení, ktorý sa skladá z troch oblastí. Na začiatku, pri nízkych napätiach, sa peny správajú lineárne elasticky, potom prechádzajú do dlhej oblasti plató (plateau), kde dochádza k nevratnej deformácii ich buniek (okrem elastických pien), a nakoniec možno sledovať oblasť s prudkým nárastom napätí (oblasť uzamknutia deformácií).


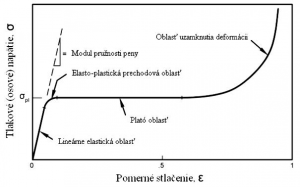
Obr. 4 Charakteristický tvar tlakovej krivky pien.

V lineárne elastickej oblasti dochádza k ohybu hrán buniek a pri uzavretých bunkách sa ešte navyše deformujú steny buniek, čo spôsobí nárast tlaku uzavretého plynu alebo kvapaliny. Pri namáhaní v tlaku dochádza v plató oblasti ku kolapsu buniek vplyvom pružného vzperu pri elastických penách (napr. guma, kaučuk), tvorením plastických zón pri plastických penách (napr. polyméry a kovy) a krehkému porušeniu pri krehkých penách ako sú napr. peny keramické.

V plató oblasti sa bunky celkom zdeformujú, až dôjde ku kontaktu protiľahlých stien buniek. S narastajúcim ďalším zaťažovaním sa voľné miesta vyplnia a pena sa začne správať ako plný materiál a napätia prudko narastú – oblasť uzamknutia deformácií. Na obr. 5 sú schematicky znázornené pracovné diagramy v tlaku pre elastické, plastické a krehké peny [1].


Obr. 5 Tlakové diagramy pien [1].

V ťahu je počiatočná lineárne elastická oblasť sprevádzaná ohybom hrán a naťahovaním stien buniek. Pri elastických penách sa hrany buniek natáčajú k osi ťahania, čo zvyšuje tuhosť štruktúry. Hrany buniek plastických pien sa tiež natáčajú k osi ťahania, dochádza k plastickému ohybu a po prekročení medze klzu daného materiálu stúpa krivka ťahového diagramu až do bodu, kde dochádza k porušeniu celistvosti materiálu.

Pri krehkých penách vzniká trhlina v najslabších miestach buniek alebo sa šíri z miesta s chybou v štruktúre bunky a je príčinou krehkého porušenia. Niektoré peny (napr. polymérové) sú plastické v tlaku a krehké v ťahu. Ťahové pracovné diagramy pre elastické, plastické a krehké peny sú schematicky znázornené na obr. 6 [1].


Obr. 6 Ťahové diagramy pien [1].

5. Absorbčné vlastnsoti

Rozhodujúcim faktorom pre určenie kvality baliacich materiálov, ochranných materiálov a absorbérov nárazovej energie je schopnosť pohltiť energiu nárazu bez prekročenia kritického napätia v týchto materiáloch alebo veľkosť zrýchlenia (spomalenia) chránenej hmoty, ktoré nesmie prekročiť dovolené hranice, aby nedošlo k jej poškodeniu alebo poraneniu v prípade osôb. A práve bunkové materiály, či už štruktúry honeycomb alebo peny, sú vhodnými pre tieto aplikácie, pretože pri rastúcej tlakovej deformácií udržujú približne konštantné napätie – plató oblasť. Táto oblasť má najväčší vplyv na pohltenie kinetickej energie chránenej hmoty.

Mechanické vlastnosti bunkových telies, a tým pádom aj plató oblasť, pri tlakovom namáhaní možno ovplyvňovať vhodným výberom základného materiálu, štruktúrou buniek a samotnou hustotou penového materiálu. Pre každú aplikáciu týkajúcu sa absorpcie nárazovej energie možno nájsť optimálnu hustotu bunkového telesa. [1, 2]

Na obr. 7 sú znázornené tlakové diagramy pre tri vzorky penového materiálu, každá vzorka má inú hustotu. Tieňované plochy pod krivkami reprezentujú rovnaké množstvo pohltenej energie. Najľahšia vzorka (hustota \rho_1) absorbuje danú energiu pri rozsiahlej deformácií, pretože má malé hodnoty napätia v plató oblasti. Vzorka sa deformuje až do oblasti zhustenia deformácií, kde zákonite prudko narastú hodnoty napätia vo vzorke.

Naopak najťažšia vzorka (hustota \rho_3) sa málo deformuje, ale hodnoty napätia sú výrazne vyššie, pretože napätia v plató oblasti sú vysoké. Optimálne sa javí vzorka so strednou hmotnosťou (hustota \rho_2), ktorej deformácie je síce väčšia oproti vzorke s najvyššou hustotou, ale dosiahnuté napätia sú najnižšie zo všetkých vzoriek. [2]


Obr. 7 Miera pohltenia rovnakého množstva energie pre peny s rôznou hustotou [2].

Pre posúdenie absorbčných vlastností sa tvoria tzv. absorbčné diagramy, ktoré zobrazujú závislosť absorbovanej energie W od napätia \sigma. Absorbovaná alebo tiež špecifická energia predstavuje plochu pod krivkou tlakového diagramu:

W = \int_0^{\varepsilon} \sigma (\varepsilon) d\varepsilon (3)

Z týchto grafou sa potom ľahko identifikujú peny s adekvátou hustotou (obr. 8). Určená hodnota absorbovanej energie je definovaná horizontálnou čiarou, ktora v jednotlivých grafoch určí penu s odpovedajúcu hustotu a hodnotu napätia v danej pene. Obálka tvorená cez W – \sigma krivky predstavuje optimum absorbovanej energie pre danú hustotu peny. [2]


Obr. 8 Absorbčný diagram peny s rôznymi hustotami [2].

Ďalšími spôsobmi ako zistiť optimálnu hustotu peny pre požadovanú hodnotu absorbovanej energie sú najmä parameter efektívnosti a parameter ideálnosti. [2] Parameter efektívnosti Ef je funkciou napätia (obr. 9). Definovaný je ako pomer absorbovanej energie W po zvolené dovolené napätie \sigma a veľkosťou tohto napätia:

E_f = \frac{\int_0^{\varepsilon} \sigma (\varepsilon) d\varepsilon}{\sigma} (4)


Obr. 9 Parameter efektívnosti [2].

Parameter ideálnosti Id je definovaný ako pomer absorbovanej energie W k súčinu odpovedajúceho dovoleného napätia \sigma a pretvorenia \varepsilon (obr. 10):

I_d = \frac{\int_0^{\varepsilon} \sigma (\varepsilon) d\varepsilon}{\sigma \varepsilon} (5)

Menovateľ v tomto prípade predstavuje ideálny absorbér, ktorého napätie je konštantné pre celý priebeh pretvorenia.


Obr. 10 Parameter ideálnosti [2].

Použitá literatúra

  1. Gibson, L. J., Gibson and Ashby, M. F.: Cellular Solids – Structure and Properties,
    2nd ed., Cambridge University Press, Cambridge, 1997
  2. M. Avalle, G. Belingardi, R. Montanini: Characterization of Polymeric Structural Foams under Compressive Impact Loading by means of Energy-absorption diagram, Int. Jouranl if Impact Engineering, 2001,vol. 25, p. 455-472.
FEI STU Bratislava, Ilkovičova 3, 812 19, Katedra mechaniky

Napísať príspevok