V každej dobe sa venuje zvýšené snaženie inžinierov, matematikov, ekonómov problematike optimalizácie procesov. Rozvoj hospodárstva si vyžaduje aplikáciu optimalizačných metód z dôvodov, ktorými sú efektívnosť, ekológia procesov a tiež samotná konkurencieschopnosť podniku.

Úvod

Zabezpečenie prosperity a úspešného rozvoja podniku v náročných podmienkach trhovej ekonomiky nie je jednoduchou záležitosťou. Zosúladenie tzv. STTEEP faktorov (sociálne, technické, technologické, environmentálne, ekonomické, politické faktory) je naozaj náročné a zložité. Musí sa však vždy vychádzať z reálného, základného materiálového toku. Výrobný proces musí zohľadniť reťazec nadväzných činnosti z hľadiska IPO diagramov (Input – Process – Output), a tiež aj veľkosť výrobnej kapacity, ktoré umožňujú určiť požadované vstupy (základné suroviny a materiály, polotovary a komponenty, pomocné materiály, náhradné diely, energie a pod.), a to nie iba v materiálovom, ale tiež aj v hodnotovom vyjadrení. [2], [3], [4], [6]

Aktuálny stav tokov vo výrobných procesoch

V procesoch výroby sa vyskytuje viacero druhov, typov tokov, a tiež vzťahov medzi nimi, tzv. logisticko – dopravný systém. V tejto práci stručne pozrieme na materiálový tok, medzi jednotlivými miestami vo výrobe.

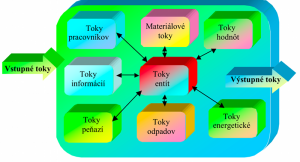
Obr. 1 Zobrazenie všeobecných vzťahov medzi tokmi entít [1, Bigoš ], [2], [3], [4], [doplnil, upravil autor]

Materiálový tok

Je kategória, pomocou ktorej okrem iných, charakterizujeme dynamiku výroby v priestore a tiež čase. Je to riadený pohyb, materiálu, surovín, polovýrobkov, rozpracovaných výrobkov, médií, nástrojov, a ďalších vo výrobe i vo sfére distribúcie. Najdôležitejšiu časť materiálového toku tvorí tok pracovných predmetov (všeobecnejšia kategória), [6]. Na materiálový tok pôsobí niekoľko činiteľov:

• objem a sortiment, druh a typ výroby
• úroveň technologickej zložitosti a členitosti procesov a montážnych celkov, skupín
• počty operácií na jednotlivých dieloch a pracovných miestach
• tvar, členitosť daného priestoru
• spôsob operačnej, medzioperačnej a medzi strediskovej dopravy
• umiestnenie pomocných, podporných prevádzok a služieb (výdaj náradia, stanovište údržby, umiestnenie kooperujúcich a outsourcujúcich výrobných útvarov, úsekov, jednotiek…)

Vlastnosti a úrovne materiálových tokov

Hľadiská:

• Dĺžka trasy materiálového toku, (topologická, časová, nákladová, …)
• Štruktúra, členitosť, organizácia materiálového toku
• Počty pracovníkov a náklady na manipuláciu, a prostriedky dopravy
• Podiel manipulačných operácií vzhľadom na zhodnocujúce činnosti
• Objemy manipulácie v jednotlivých kategóriách
• Spojené náklady, poistné, špedičné, colné, daňové, bezpečnostné, cestné, poštovné, …

Štruktúru materiálového toku možno analyzovať z hľadiska jeho komponentov, a tiež aj z hľadiska fáz materiálového toku. Medzi jeho základné prvky (komponenty) patria:

• materiál – jeho druh, vlastnosti, množstvo, frekvencia pohybu
• manipulačné prostriedky – ich druh, funkčné vlastnosti, parametre
• dopravné cesty – ich tvar, profily, únosnosť, povrch, stúpanie

Z hľadiska dostupnosti fáz materiálového toku možno jeho štruktúru rozložiť do týchto časti:

• vonkajšia, závodná doprava, mimopodnikový transport
• nákladka a vykládka prijímania materiálu
• zásobovacie sklady a vnútro skladová manipulácia
• medziobjektová doprava
• operačná manipulácia
• medzioperačná doprava
• sklady vo výrobe
• manipulácia s odpadom, produktom, obalom
• kompletovanie, balenie výrobkov, ich paletizácia, kontajnerizácia a expedícia.

Zdokonaliť štruktúru materiálového toku predpokladá diagnostikovať každú jeho fázu, jej vlastnosti a hľadať možnosť optimalizácie zásobovania a ďalšie optimá, od ktorých závisí optimálne usporiadanie výroby v priestore a plynulý aj materiálový tok.

Základné činnosti pri toku materiálu

• Technologické operácie – spracovanie súčiastok, resp. ich montáž s inými súčiastkami, dielmi…
• Doprava – prepravovanie, ukladanie, zdvíhanie, spúšťanie… t.j. pohyb v akomkoľvek smere, čakanie na operáciu, doba operácie, časy ustálenia,
• Skladovanie, časy identifikácie, merania, váženia, počítania, evidencie, konfirmácie, potvrdenia, verifikácie, archivácie,
• Technická kontrola – kvality i kvantity
• Zdržanie – čakanie na uvoľnenie pracovísk, dopravných zariadení, voľnosti ciest, …

Klasická optimalizácia tokov

Optimalizovať materiálový tok znamená hľadať jeho ideálnu úroveň, nepretržitý pohyb materiálu pri minimálnych nákladoch, spotrebe času, energii, prostriedkov, pracovníkov, alebo iných kritériách, ako sú napr.:

• dĺžka prepravnej vzdialenosti,
• objem prepravy za jednotku času, veľkosť, kapacita, nosnosť prepravnej jednotky
• dopravné náklady,
• využitie ložného priestoru (objemu),
• čas trvania dopravných operácií a pod.

Kriteriálnu funkciu je vhodné zostavovať a zostaviť ako viac zložkovú, so zachytením aj ďalších cieľov: maximálne uspokojiť požiadavky na premiestňovanie materiálov na určené miesta pri súčasnom minimalizovaní nákladov na túto dopravu. Popri lineárnych, spojitých, diskrétnych a deterministických metódach sa pri manipulačných analýzach používajú aj stochastické, evolučné, genetické, hierarchické, sieťové a behaviorálne metódy, pomocou ktorých možno optimalizovať:

• potrebu (počet, spolu využitie, substitúcia) manipulačných prostriedkov, prípravkov, pomôcok
• náklady, časy
• potrebu pracovníkov,
• veľkosť celkového materiálového toku, spojitosť a pretržitosť, …

Veličiny, premenné, parametre, limitujúce podmienky vstupujúce do optimalizácie sú nielen jednotlivé hodnoty, ale najmä časové rady. V systéme je tiež možné využiť prepojenie na existujúce zákaznícke predikčné systémy, statické a dynamické modely sústav a podobné podporné nástroje.

Vstupy pre optimalizáciu

Medzi podstatné vlastnosti, ktoré je potrebné brať do úvahy, patria predovšetkým:

• dostupnosť daného základného materiálu (suroviny), a to nielen z krátkodobého, ale aj z dlhodobého hľadiska (materiál musí byť k dispozícii v priebehu celej doby existencie modelu výroby),
• možnosť substitúcie daného materiálu v prípade jeho nedostupnosti (táto možnosť substitúcie úzko súvisí s technológiami, pričom značné obmedzenie, či nemožnosť substitúcie ovplyvňuje mieru rizika modelu výroby),
• kvalita materiálu a suroviny sa posudzuje pomocou určitého súboru fyzikálnych a chemických vlastností, odlišná kvalita môže ovplyvňovať nielen voľbu technologického procesu (napr. nízka kvalita vylučuje určitú technológiu), ale spravidla pôsobí na nákladovú stránku výrobného procesu. Vo viacerých prípadoch môže mať rozhodujúci vplyv na posudzovanie kvality základného materiálu a surovín požadovaná kvalita finálneho produktu,
• vzdialenosť zdrojov materiálu (suroviny), ktorá ovplyvňuje výšku dopravných nákladov (pozornosť je nutné venovať i možným spôsobom transportu zahŕňajúcim železničnú, lodnú a automobilovú prepravu, ich prednostiam, nedostatkom a dopadom na náklady),
• miera rizika spojená so zabezpečovaním daného materiálu alebo suroviny, čím sú zdroje materiálu vzdialenejšie, tým sú väčšie nebezpečenstvá porúch v plynulosti zásobovania a tým je väčšia potreba vytvárať aj väčšie poistné zásoby na ich preklenutie,
• cenová úroveň materiálu (suroviny), ktorá sa bezprostredne premieta do výrobných nákladov a ovplyvňuje tak efektívnosť modelu výroby.

I keď sú základné suroviny a materiály v rámci vstupov do modelu najvýznamnejšie nemôže sa v technicko-ekonomickej oblasti zabúdať na ďalšie zložky týchto vstupov. Patria tu:

• rôzne druhy polotovarov, montážnych dielov a komponentov, musia sa stanoviť požiadavky na tieto vstupy, ich dostupnosť a cenová úroveň,
• pomocné materiály a náhradné diely,
• energia (elektrická energia, palivo, voda, stlačený vzduch, technické plyny, …).

Pozorne musíme predovšetkým posudzovať požiadavky na energiu. I keď detailné vyhodnotenie jednotlivých zložiek energie je možné až po voľbe umiestnenia a technológie, je nutné odhadnúť výšku potrieb jednotlivých druhov energie, posúdiť existujúce zdroje a ich obmedzenosť a prijať včas opatrenia na dostatočné zaistenie energií. Nároky na materiálové vstupy a energiu umožňujú stanoviť niektoré nákladové veličiny (resp. veličiny, od ktorých tieto náklady závisia), ktoré tvoria súčasť vstupných údajov pre posudzovanie ekonomickej efektívnosti. Prehľadný súhrn nákladových veličín, ktoré sa týkajú materiálových vstupov a energii by mal obsahovať:

• názov materiálového vstupu, resp. energie a jednotku merania,
• normu spotreby na jednotku vyrábaného produktu,
• očakávaná nákupná cena jednotky materiálového vstupu či energie,
• očakávané náklady na jednotku produkcie,
• očakávané náklady na predpokladaný (plánovaný) objem produkcie.

Prepočty potrieb materiálových vstupov a energií umožňujú tiež stanoviť očakávanú výšku materiálových zásob s dopadom na finančnú stránku modelu (materiálové zásoby viažu nielen dlhodobé finančné prostriedky, ale na ich skladovanie je treba vybudovať skladové kapacity, tj. vynaložiť jednorazové určité investičné náklady).

Súčasná technologická schéma – materiálový tok – je posudzovaná z hľadiska normovaných výkonov a z hľadiska energetických požiadaviek. Pre zabezpečenie plynulosti materiálového toku sa sústreďuje vysoká pozornosť na dodržiavanie kapacitných parametrov jednotlivých uzlov, na pravidelné meranie výstupov z uzlov z hľadiska štandardizovaných kvalitatívnych parametrov a povolených limitov.

Výstupy optimalizácie

Výstupom krátkodobej optimalizácie je u prechodného stavu prerozdelenie požiadaviek na jednotlivé zdroje a tým samozrejme aj na nákup primárnych zdrojov a predaj vyrobených produktov pri zohľadnení všetkých optimalizačných kritérií. V ustálenom režime je výsledkom optimalizácie z rozličných hľadísk optimálny chod jednotlivých technologických celkov. Dlhodobá optimalizácia hľadá optimálnu konfiguráciu všetkých procesov výroby ako celku pre dosiahnutie dlhodobej maximálnej ziskovosti.

Účelová, nákladová, objektivizačná, zisková, výnosová, sankčná, trestová pokutová, kriteriálna funkcia

Algoritmami optimalizácie sa hľadá minimum vytvorenej účelovej funkcie – systému rovníc, obmedzujúcich podmienok, nezávisle premenných predstavujúcich prevádzkové režimy jednotlivých zdrojov, statické parametre zdrojov, konfiguráciu celého energetického hospodárstva. Účelová funkcia sa zostavuje s cieľom numericky hodnotiť stupeň priblíženia sa k existujúcemu reálnemu optimu:

• maximalizácie účinnosti jednotlivých zdrojov
• maximalizácie úspory primárnej energie
• minimalizácie nákladovej funkcie, času
• minimalizácie doby návratnosti
• minimalizácie množstva emisií a ďalších

pričom hlavným kritériom je efektivizácia výnosov (zisku) z dlhodobého hľadiska.

Modelovanie a štruktúra optimalizácie

Základom pre optimalizáciu je vytvorenie sústavy modelov jednotlivých technologických celkov, ich interakcií s vonkajším prostredím, modelov obchodných vzťahov s dodávateľmi i odberateľmi a komplexného modelu všetkých distribučných procesov ako celku. Štruktúra optimalizácie sa tým stáva kaskádovou a optimalizujú sa:

• chod sústavy v ustálenom stave
• prechodové stavy

Niektoré metódy pre optimalizáciu tokov materiálov

Jednotlivé metódy zahŕňajú v sebe širšie možnosti, niektoré klasických metód (km) sú to: metóda priameho riešenia systému stacionárnych rovníc (nerovníc), metóda priameho porovnávania funkčných hodnôt, hľadanie extrému funkcií s jedným lokálnym optimom (extrémom), metódy využívajúce derivácie, jednoduchá gradientová metóda, metóda najväčšieho spádu, metóda druhého rádu (Newtonová metóda, Newton – Raphsonová metóda), Gausová – Newtonová metóda, metóda priameho hľadania extrému funkcie, Simplexová metóda, relaxačná metóda (Probe algoritmus), Rosenbrocková metóda, optimalizácia s ohraničeniami typu rovnosti (nerovnosti), Lagrangeové multiplikátory, lineárne programovanie, metóda projekčných gradientov, metóda pokutových funkcii, metóda zlatého rezu, Fibonacciho metóda, Powelová metóda, (GRG) metóda zovšeobecného redukovaného gradientu, Nelderová – Meadová metóda, dynamické programovanie, princíp maxima, Bellmanová metóda, Pontrijagonová metóda, Vogelová, metóda severozápadného rohu (NWC), metódy najmenšieho prvku, v riadku, v stĺpci, v matici, Russelová, maďarská a viacero ďalších.

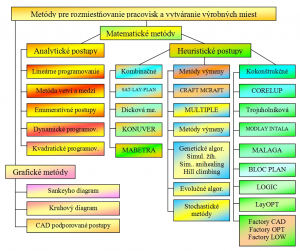
Obr. 2 Ilustrácia taxonómie neiktových optimalizačných metód, [2], [3], [4], [doplnil, upravil autor]

V nasledujúcej časti uvedieme ilustratívny jednoduchý príklad so zjednodušeným zobrazením postupu.

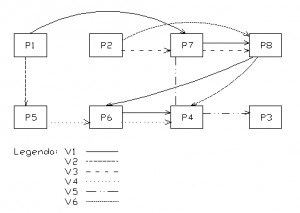
Opis pôvodného stavu materiálového toku

V zjednodušenom výrobnom systéme sa vyrába konkrétny výrobný sortiment (V1, V2, .. V6 – výrobky). Výroba je realizovaná technologickými operáciami zabezpečovanými na jednotlivých pracoviskách (P1, P2, … P8 – pracovné miesta). Výrobný postup každého typu výrobku je iný. Cieľom je aby umiestnenie a prístup k jednotlivým strojom vytváral optimálne podmienky zabezpečovania výroby daného výrobného sortimentu. Úlohou je ukázať jednoduchý model hodnotiaci konkrétnu situáciu a následné naplánovanie nových tokov pre docielenie lepšej efektivity výroby.

Obr. 3 Pôvodný materiálový tok, [5]

Tab. 1 Sortiment výrobkov a pracovísk

Pracovisko/ Výrobok	P1	P2	P3	P4	P5	P6	P7	P8
V1	1			1		1	1	1
V2	1				1
V3		1					1	1
V4				1	1	1
V5			1	1			1
V6		1		1				1

Hodnota kriteriálnej funkcie v pôvodnom materiálovom toku je 52.

Návrh riešenia materiálového toku

Situácia je opísaná v tabuľke, kde prázdne políčko znamená u daného výrobku neúčasť na danom technologickom mieste. Hodnota 1 značí, že na danom výrobku, mieste je potrebné vykonať operáciu (zjednodušene) na danom pracovisku, teda je nutné tento polotovar na pracovisko dopraviť a potom znova odoslať z daného pracoviska. Optimalizácia spočíva v takej organizácií umiestnenia strojov, aby presuny výrobkov (polotovarov) bol čo najefektívnejší.

Pri organizácií výroby vznikajú požiadavky na efektívnejšie preusporiadanie topológie z novým sortimentom požiadaviek, t. j. nová štruktúra výrobného programu z hľadiska početnosti výrobkov a druhov operácií aplikovaných počas výroby. Čím sú jednotlivé umiestnenia operácií na pracoviskách bližšie ku hlavnej diagonále tabuľkového zápisu, tým je efektívnejší spôsob zabezpečovania pohybu medzi jednotlivými operáciami. Teda úlohou je preusporiadať pracoviska tak, aby tabuľkové zobrazenie bolo rozptýlené (primknuté) okolo hlavnej diagonály.

Ideálny stav by sa dosiahol, ak by sa výrobky vyskytovali iba po hlavnej diagonále, resp. v susedných poliach. Cieľom je usporiadať stroje v linke tak, aby počas procesu výroby jednotlivé polotovary iba minimálne vynechávali jednotlivé pracoviská v linke. To my dovoľuje vytvoriť funkciu váženého súčtu vzdialenosti od diagonály. Tento zápis je dobre reprezentovateľným zápisom reálneho stavu linky a môže sa vytvoriť zjednodušená kriteriálna funkcia na vyhodnocovanie úrovne efektívnosti (optimálnosti) zostavenia linky. Je to matematický model hodnotenia vzdialenosti od minima funkcie. Hodnotu kriteriálnej funkcie vyjadríme:

(1)

Uf(x_ij) – hodnota účelovej funkcie, x_ij – nezávislá premenná analyzovanej funkcie, p_v – počet druhov výrobkov, p_o – počet operácií, i, j – poloha aktuálnej operácie na príslušnom polotovare v tabuľke

V prípade nerovnakej početnosti jednotlivých druhov výrobkov je potrebne upraviť účelovú funkciu vzhľadom na nerovnakú váhu jednotlivých operácii. Tento optimalizačný výpočet nasleduje po preverení primeranosti kapacity pre daný výrobný sortiment a počet. Potom kriteriálna funkcia má tvar

(2)

n_i – početnosť i-tého výrobku, e_i – ekonomický ukazovateľ i-tého výrobku, z_i – záťažový ukazovateľ i-tého výrobku

Po vykonaní viacerých alternatív usporiadaní pracovísk, uvedieme jedno z možných riešení. Iné varianty si môže každý záujemca jednoducho zobraziť a vyhodnotiť.

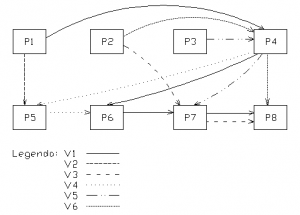
Variant č. 4

Vo variante číslo 4 sú zaradené pracoviska v poradí P1, P2, P7, P8, P5, P6, P4, P3.

Tab. 2 Hodnota kriteriálnej funkcie pre variant 4, [5]

41	P1	P2	P7	P8	P5	P6	P4	P3
V1	1		1	1		1	1
V2	1				1
V3		1	1	1
V4					1	1	1
V5			1				1	1
V6		1		1			1

Hodnota kriteriálnej funkcie pre 4 variant riešenia je 41.

Zhodnotenie

Pre zjednodušenie situácie čitateľom je uvedené grafické zobrazenie zhodnotenia a porovnania niektorých navrhovaných variantov riešenia materiálových tokov v procese výroby.

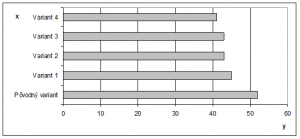
Obr. 4 Porovnanie alternatív riešenia materiálového toku, [5]

Na osi x sú zobrazené jednotlivé alternatívy tokov a tiež aj pôvodný stav. Na os y sú zobrazene hodnoty účelovej funkcie (dĺžky jednotlivých ciest) materiálových tokov. Uvedený graf jasne ukazuje najvhodnejšiu alternatívu, najlepší navrhnutý variant riešenia z viacerých navrhnutých možnosti je variant štyri. Tento má dĺžku materiálových tokov 41 čo je o 11 jednotiek menej ako pôvodný stav.

Obr. 5 Variant číslo 4, [5]

Záver

Optimalizácia materiálového toku predstavuje možnosť pre výrobu získať okrem finančných úspor aj skrátenie výrobných časov. Cieľom nasledujúcich možných riešení je zabezpečiť dobrú koordináciu materiálových tokov a vhodné rozmiestnenia výrobných miest (pracovísk), aby pohyb materiálu a výrobkov bol, čo najbližšie optimálnemu predovšetkým z hľadiska znižovania náročnosti, minimalizovania nákladov na manipuláciu s materiálom.

Znázornením transportných trás boli zobrazené riešenia pre skrátenie a sprehľadnenie materiálového toku. O vhodnosti usporiadania vo výrobnom procese hovorí veľkosť hodnoty kriteriálnej (účelovej) funkcie, čo možno vnímať ako jednojednoznačný číselný ukazovateľ a zjednodušenie procesu riešenia. Tieto a ďalšie vlastnosti uvedených metód prinášajú podmienky pre prácu s matematickým obrazom reality, bez ohľadu na použitý druh optimalizačného mechanizmu.

Ďalšie možnosti optimalizácie materiálového toku, ktoré táto práca prináša, môžu viesť k dosiahnutiu ešte vyšších cieľov, to predstavuje optimalizáciu aj z hľadiska časového usporiadania materiálového toku, a tiež optimalizáciu veľkosti zásob. Dôležitým predpokladom optimalizácie materiálového toku je správne fungujúci informačný systém, ktorý poskytuje relevantný prehľad o stave a pohybe materiálu v rámci celého výrobného procesu, t.j. o príjmu materiálu (surovín) až po expedíciu hotových výrobkov, čo umožňuje kompetentné, reliabilné riadenie procesov.

Zoznam použitej literatúry

1. Bigoš, Peter – Kiss, Imrich – Ritók, Juraj – Kastelovič, Eduard: Materiálové toky a logistika II. Košice: TU, 2005. ISBN 80-8073-263-9
2. Hricová, Romana: Stratégia umiestnenia výrobkov na nové trhy, In: Sociokultúrna realita a príroda, Prešov : FVT TU, 2007 S. 209-214. – ISBN 9788080737283
3. Matisková, Darina: Automatic of component production and minimalization of production costs, In: Acta Technica Corviniensis. Vol. 5, no. 2 (2012), p. 103-106. – ISSN 2067-3809
4. Pavlenko, Slavko – Matisková, Darina: Stratégia výberu technológii rezania materiálov, In: Management of manufacturing systems. – Prešov : FVT TU, 2004 S. 151-155. – ISBN 8080732094
5. Pištej, Marián: Optimalizácia topológií materiálového toku v procese výroby. Prešov: Technická univerzita v Košiciach, Fakulta výrobných technológií v Prešove, 2008. 45 s.
6. Šebej, Peter: Optimalizácia topológie výrobných liniek a organizácia tokov vo výroby, využitím matematických prostriedkov, In: Nové trendy v prevádzke výrobnej techniky 2003. – Prešov : TU-FVT, 2003 S. 399-403. – ISBN 8080730598