O specifičnosti varianty GPC prediktivního řízení (Generalized Predictive Control) bylo pojednáno v předchozích článcích na tomto odborném portále. Mezi další nezvyklé výhody GPC je řízení procesů s dopravním zpožděním, jenž jiné přístupy málokdy nabízí. To je neobvykle snadné, a to pouze navýšením parametru minimálního horizontu na hodnotu jedna plus dopravní zpoždění.

Tento přístup je velice lákavý. Cílem článku je tuto možnost prověřit po stránce efektivnosti, jestli není lepší použít variantu, kdy je nejprve zkorigováno samotné dopravní zpoždění u procesu a pak jeho řízení klasickým GPC algoritmem. Zapojení s korekcí dopravního zpoždění je známé jako Smithův prediktor. Výsledky simulací mohou být čtenáři nápomocny při volbě jedné z těchto dvou variant, a to z pohledu kvality řízení nebo přijatelnějšího schématu zapojení.

Systém s dopravním zpožděním a jeho eliminace Smithovým prediktorem

Pro jednorozměrový diskrétní systém druhého řádu (1) se přidefinuje dopravní zpoždění sériovým připojením diskrétního přenosu tohoto zpoždění, což je Z-obraz (2) v podobě proměnné z umocněné na zápornou hodnotu dopravního zpoždění. Sériové řazení přenosů dává v blokové algebře teorie systémů výsledný přenos daný součinem těchto dílčích přenosů. Tím obdržíme výsledný matematický model systému (3) s modelem dopravního zpoždění (2).

Z analogie sériového přidání modelu dopravního zpoždění se vychází i při namodelování systému typu (3) v prostředí MATLAB/Simulink. V obvodu (Obr.1) je schéma nadefinování objektu (3) pomocí obvodových prvků typu Discrete Transfer Fcn a Unit Delay. Pro zpoždění rovné jedna je přítomen právě jeden prvek typu Unit Delay. Pro zpoždění větší než jedna je nutné jejich vícenásobné zařazení za sebou, a to v počtu odpovídajícímu právě hodnotě dopravního zpoždění.

(1)

(2)

(3)

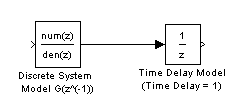
Obr.1 Schématické vyjádření diskrétního systému s dopravním zpožděním(model v sériovém zapojení s modelem zpoždění) v prostředí MATLAB/Simulink

Dopravní zpoždění lze eliminovat zapojením zvaným Smithův prediktor (Obr.2). Lze jej blíže nastudovat v publikaci [3]. Toto zapojení nám pomůže, v jedné z testovaných variant uvedených dále, dopravní zpoždění ze systému odstranit a pracovat s ním, jako by žádné nevykazoval.

Obr.2 Smithův prediktor pro eliminaci dopravního zpoždění s rozlišením model/systém

Varianta GPC prediktivního řízení s možností pracovat s procesy se zpožděním

Obr.3 GPC regulátor s rozšířeným nastavením dokáže řídit i systém s dopravním zpožděním

Varianta korekce zpoždění Smithovým prediktorem a následným GPC řízením bez zpoždění

Alternativní varianta je vůbec dopravní zpoždění u řízeného systému neuvažovat, a to konkrétně po korekci prediktorem dle Smitha. Následně pracovat klasickým GPC řízením s nastavením jako u systémů bez zpoždění (Obr.4).

Obr.4 Po korekci systému s dopravním zpožděním Smithovým prediktorem jej lze řídit klasicky GPC algoritmem

Porovnání uvedených variant regulace procesů se zpožděním v MATLABu

Realizace první a druhé varianty se Smithovým prediktorem a klasickým prediktivním GPC řízením byla provedena v programu MATLAB. Pro testování obou způsobů byl použit model procesu (1) se dvěmi variantami dopravního zpoždění o hodnotách jedna – model (4) a dva – model (5). S diskrétními přechodovými charakteristikami (Obr.5). Tyto procesy byly řízeny obouma variantama. Výsledky řízení (Obr.6), (Obr.7) jsou zhodnoceny v závěru tohoto odborného článku.

(4)

(5)

Obr.5 Přechodové charakteristiky v programu MATLAB pro systémy (4)(vlevo) a (5)(vpravo)

Obr.6 Výsledky řízení systému (4)(vlevo) a (5)(vpravo) algoritmem GPC bez Smithova prediktoru (vyšší nastavení parametru lambda navíc omezilo vyšší kmitavost)

Obr.7 Po aplikaci druhé varianty se Smithovým prediktorem je samozřejmě pro oba systémy (4) i (5) GPC řízení shodné

Závěr

Předkládaný článek se zabývá specifickou vlastností GPC řízení, a to ovládáním systémů s dopravním zpožděním. Do této množiny v praxi patří řada procesů, neboť má spojitost s přenosem energie. Předmětem zkoumání zde bylo porovnat řízení systémů s dopravním zpožděním GPC algoritmem s klasickým schématem (Obr.3), ale s nepatrně pozměněným nastavením jednoho z jeho parametrů. Tato modifikace má za následek umožnění řízení právě systémů se zpožděním. Situaci bez této modifikace prezentuje druhá doporučená varianta se schématem (Obr.4), kdy bude zachováno běžné nastavení GPC regulátoru, ale za předpokladu, že zpoždění u procesu eliminujeme. Toho lze docílit korekcí tzv. Smithovým prediktorem, jenž je zakomponován právě do druhé ekvivaletní varianty práce s procesy probíraného charakteru.

Cílem článku bylo porovnat přínosy obou variant na řízení jednorozměrových procesů se zpožděním (4) a (5). Druhá varianta se Smithovým prediktorem redukovala zpoždění a zvýšila hladkost průběhu výstupu systémů (Obr.7). Algoritmus GPC bez Smithova prediktoru řídil sice systémy v pořádku (Obr.6), ale kvalita byla o něco horší. Je to dáno tím, že samotné zpoždění přináší do řízení nestabilní charakter chování. To u druhé varianty nebylo, protože bylo zpoždění eliminováno. Na závěr bych doporučil obě varianty. Je excelentní, že GPC regulátor po nepatrné modifikaci svého nastavení dokáže řídit i systémy s dopravním zpožděním, což bylo potvrzeno. Je ale také nabídnuta velmi kvalitní varianta s použitím Smithova prediktoru.

Poděkování

Článek byl uskutečněn za finanční podpory IGA Univerzity Tomáše Bati ve Zlíně, Fakulty aplikované informatiky číslo IGA/FAI/2012004.

Reference

1. BAROT, T., KUBALČÍK, M. Studium závislosti výpočetního času algoritmu GPC prediktivního řízení na volbě typu popisu matematického modelu v regulátoru. POSTERUS.sk, portál pre odborné publikovanie, 2012, ISSN 1338-0087.
2. PROKOP, R, MATUŠŮ, R., PROKOPOVÁ, Z. Teorie automatického řízení – lineární spojité dynamické systémy. 1.vyd. Zlín: Univerzita Tomáše Bati ve Zlíně, Fakulta aplikované informatiky, 2006. 102 s. ISBN 80-7318-369-2.
3. BALÁTĚ, Jaroslav. Automatické řízení. 1.vyd. Praha: Nakladatelství BEN – technická literatura, 2003. 664 s. ISBN 80-7300-020-2.
4. CORRIOU, J.-P., 2004. Process control: theory and applications. London: Springer. ISBN 1-85233-776-1.
5. KUBALČÍK, M., BOBÁL, V., 2011. Computation of predictions in multivariable predictive control, Proceeding ACMOS’11 Proceedings of the 13th WSEAS international conference on Automatic control, modelling & simulation. ISBN 978-1-61804-004-6.

---

Spoluautorom článku je M. Kubalčík, Ústav řízení procesů, Fakulta aplikované informatiky, Univerzita Tomáše Bati, nám. T. G. Masaryka 5555, 760 01 Zlín, ČR.