Battery models capture the characteristics of real life batteries, and can be used to predict their behavior under various operating conditions. In this paper, a dynamic model of lithium-ion battery has been developed with MATLAB/Simulink® in order to investigate the output characteristics of lithium-ion batteries for vehicle applications. Dynamic simulations are carried out, including the observation of the changes in battery terminal output voltage under different charging/discharging temperature and cycling conditions.

In the work are described characteristics of choice for electric vehicle battery through a mathematical calculation. Model Battery system is created in MATLAB/Simulink®. The results in the end show characteristic battery energy for the electric car.

1. Introduction

The worldwide decline in oil raises several questions in terms of transporting people and goods. Searching for answers question of what kind of energy will provide a vehicle movement – which energy source will be useful in future course with respect on the environment. At present, the choice seems to be promising for electricity drive vehicles. Among the most basic advantages of the electric power is higher overall efficiency, smaller size electric motor, quieter, zero air pollutants that emits during moving vehicle. Since changing the energy source that is used to propel the vehicle, be adapted to a vehicle drive train. Therefore, the choice of a suitable battery tray as electricity, which is useful for electric power vehicle.

There are various methods for energy storage, energy through electrical, or magnetic field or electrochemical method, where the traditional method based on electrochemical conversion – batteries (Fig.1). The problem of electrochemical conversion and storage is a small volume and mass energy density and long duration of the chemical process that prevents the immediate notion of relatively large amounts of energy. Although it has been recently a significant improvement of these parameters (Ni-MH, Li-Ion, Li-Ion batteries), there is still a major unsolved problem of energy transfer in short intervals and low efficiency of energy conversion.

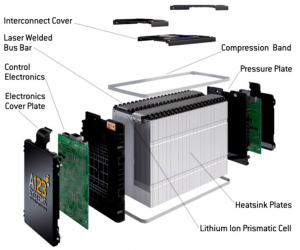
Fig. 1 Battery system with control electronics and cover plates for electric mobile and stationary applications

There are other methods of saving, which saves it as a form of kinetic energy (flywheel). These methods already in use prior to II. World War II, the Swiss railways. In these methods, there is imposed through the necessary transformation of energy from one form to another, where it plays an important change.

Among the various existing rechargeable batteries, lithium-based batteries appear to occupy a prime position in various aspects [1]. Lithium-ion batteries, with high energy density, high operating voltage levels and long cycle life, have been extensively used in the portable electronic devices, cellular phones and camcorders etc. [2]. In order to evaluate the battery performances under different conditions without resorting to time consuming (and expensive) prototyping and measurement for each alternative, there is a strong need for accurate battery models. Battery models capture the characteristics of real-life batteries, and can be used to predict their behavior under various conditions of charge/discharge. They can also be used to make suggestions towards the improvement and the optimization in battery system [3].

For better understanding of the performance of lithium-ion batteries, numerous authors have developed various models [4-6]. Despite of being prosperous in many aspects, most of them still have several drawbacks. Some of them ignore the transient behaviors [7], while some only work for a fixed state of charge [8] or unable to predict battery runtime [9] which is an important factor for judging the battery performance.

Chen and Mora [10] proposed a battery model that can predict both battery runtime and I-V performance accurately by combining the transient behaviors of battery with a variable open circuit voltage and internal resistance. Besides, the effect of temperature and capacity fading on battery dynamics is neglected in [10]. However, thermal behavior of lithium batteries is important for both the battery operating life requirements and safety considerations [11, 12]. Furthermore, the effect of capacity fading is also important for both predicting the battery cycle life exactly and determining the remaining usable battery capacity [6,13,14].

A more accurate battery model can be obtained by considering the impacts of these significant parameters. In this study, we established an effective dynamic lithium ion battery simulation model in MATLAB/Simulink environment. The battery model is developed experimentally through the [10], by adding the significant temperature and capacity fading effects on battery dynamics. Dynamic simulations are used to verify the performance of the developed lithium-ion battery model.

2. Analysis of the possibility of modeling rechargeable battery systems

Battery systems play an important role in electric vehicles should be good model in the simulation tool, representing the actual behavior of the battery. there are many cell types and the many factors that affect battery performance. Predict battery power, there are various mathematical models. None of these models are completely accurate; any need to include all factors affecting performance. Factors that affect battery performance is:

• State of charge (SOC)
• Battery storage capacity
• Rate of charge/discharge
• Temperature
• Age life

According to what is needed in the simulation, a model for battery is constructed. Generally the models proposed by several scientists could be categorized into 5 groups:

• Electrochemical battery models
• Equivalent circuit battery models
• Dynamic Lumped parameters battery model
• Finite element type models
• Tabulated battery data used models.

The simplest models are based on electrochemistry. These models ignore thermodynamic and quantum effects. Consequently, while these models can predict energy storage they are not able to model phenomena such as the time rate of change of voltage under load, they include temperature and age effects.

2.1 Electrochemical battery models

The simplest models are based solely on electrochemistry. These models ignore thermodynamic and quantum effects. Consequently, while these models can predict energy storage they are not able to model phenomena such as the time rate of change of voltage under load nor do they include temperature and age effects [18]. The Peukert equation is a convenient way of characterizing cell behavior and of quantifying the capacity offset in mathematical terms. This is an empirical formula which approximates how the available capacity of a battery changes according to the rate of discharge [16].

(1)

Where: I – discharge current [Amp], n – battery constant (n=1.35 for typical lead-acid batteries), T_i – time to discharge at current I [Seconds], C – theoretical capacity of the battery [Ampere hour]

The state of charge (SOC) at a constant discharge rate is:

(2)

For non-constant discharge rates the above equation must be modified and evaluated in small time steps:

(3)

Where: C – capacity of the battery, Subscripts 1 and 2 refer different discharge-rate states

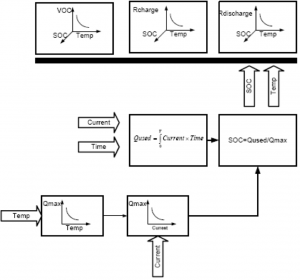
Fig. 2 Nonlinear dynamic battery model using the knowledge of the Thevenin battery model

2.2 Shepherd Model Equation

The Shepherd model is perhaps the best known and most often used battery model for Hybrid vehicle analysis. The model describes the electrochemical behavior of the battery directly in terms of voltage and current. It is often used in conjunction with the Peukert equation to obtain battery voltage and state of charge given power draw variations [17]:

(4)

Where: E_t – battery terminal voltage [Volts], E_o – open circuit voltage of a battery cell when fully charged [Volts], R_i – internal (ohmic) resistance of the battery [Ohms], K_i – polarization resistance [Ohms], C – battery capacity [Ampere-hour], I – instantaneous current [Amps], q – accumulated ampere-hours divided by full battery capacity

2.3 Thevenin battery model

Another basic battery model describes a battery with an ideal battery voltage (E_oc), internal resistance (R), a capacitance (C_o) and over voltage resistance (R_o) (Fig.3) [18]. The disadvantage of this model is that all the parameters in this model are constant but in reality these parameters are changing according to temperature and state of the charge of the battery.

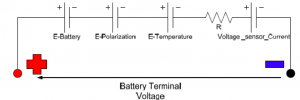
Fig. 3 Modified Thevenin model [4].

3. Simulink battery model

Model rechargeable battery system is based on the nonlinear model calculation using the knowledge of the modified Thevenin battery model. All parameters, including the charging and discharging the battery and resistor, an open perimeter of battery voltage, charge level and temperature were given either theoretically or acquired pursuant to the battery manufacturer’s data.

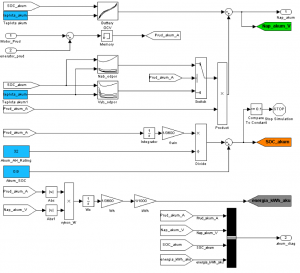
Fig. 4 Battery model created in MATLAB/Simulink environment

Model inputs is desired by discharge current or charging current. The basic key features of rechargeable battery system for non-linear calculation are:

• The characteristic dependence on temperature, battery voltage and charge state (Fig. 5)
• The characteristic dependence of the internal resistance of the battery temperature and state of charge while charging (Fig. 6)
• The characteristic dependence of the internal resistance of the battery temperature during charging and discharging state (Fig. 7)

According to required power using analytical solutions to the current battery capacity in small increments calculated loss of capacity, whose establishment is made up of current flowing through the resistance of the battery and battery charging at any time or discharging mode. Battery capacity is mathematically converted to a value of SOC is given in percent.

The characteristic dependence on temperature, battery voltage and charging conditions, the characteristic dependence of the internal resistance of the battery temperature and charge state during charging, the characteristic dependence of the internal resistance of the battery temperature during charge and discharge status are entered into workspace software environment MATLAB and Simulink programming environment has been implemented for battery model 1-D lookup table that are needed for dynamic calculation of the value of battery voltage and internal resistance of the battery (Fig. 4). Parameters which are measured on the output of the battery system are:

• battery state of charge
• output value of battery voltage
• energy consumed in kWh from battery system

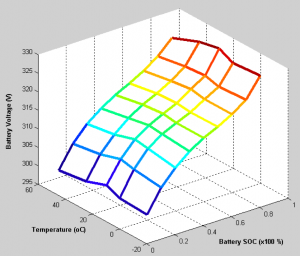
Fig. 5 Dependence of the battery voltage on the SOC and temperature

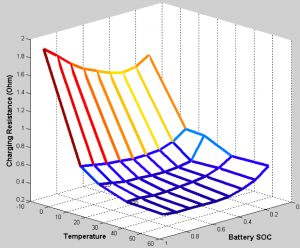
Fig. 6 Dependence of the battery charging resistance on the SOC and temperature

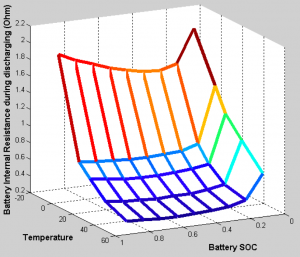
Fig. 7 Dependence of the battery discharging resistance on the SOC and temperature

4 Results

Battery system was integrated into the electric vehicle drive system.

4.1 Results of the first simulation

The initial battery charge was set to 90 percent. The simulation will stop, if the battery SOC reached 20 percent capacity. The temperature of the battery at the beginning of the simulation was 45 Celsius. For loading an electric traction system and discharging battery system was selected ARTEMIS driving cycle. Traveled distance of electric vehicle after 1000 seconds is 17 kilometers (Fig.8). Depth of battery discharge after 1000 seconds is 14 percent. On the latest graph on figure 9 is evident decrease of voltage in the battery system during simulation analogously during energy loading.

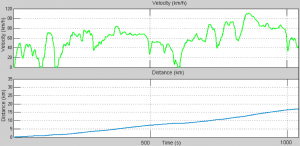
Fig. 8 Graph of electric vehicle velocity and travelled distance in time

First graph- velocity (km/h) in time, Second graph- Distance (km) in time

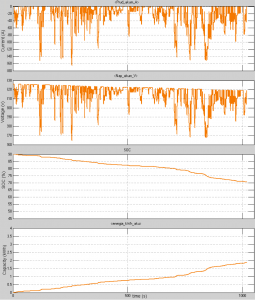
Fig. 9 First Simulation output characteristics of battery system

First graph- Battery current (Amp), Second graph – Battery voltage (V), Third graph- State of charge (%), Fourth graph- Capacity of energy in battery system (kWh)

4.2 Results of the second simulation

The initial battery charge was set to 90 percent. The simulation will stop, if the battery SOC reached 20 percent capacity. The temperature of the battery at the beginning of the simulation was 15 Celsius. For loading an electric traction system and discharging battery system was selected ARTEMIS driving cycle too. Traveled distance of electric vehicle after 1000 seconds is 17 kilometers (Fig.10). Depth of battery discharge after 1000 seconds is 21 percent.

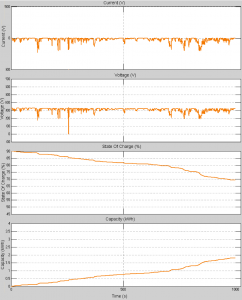
Fig. 10 Second simulation output characteristics of battery system

First graph- Battery current (Amp), Second graph – Battery voltage (V), Third graph- State of charge (%), Fourth graph- Capacity of energy in battery system (kWh)

5. Conclusion

Electric drive vehicles are promising transport solution for goods and people in the future. For electrical energy system is suitable to use nickel-based batteries, lithium batteries and new, technologically advanced battery systems. As the development of different types of batteries still going on it is possible already anticipated in the near future serial equalization of road vehicles will store energy in those batteries. An indispensable part of development is not only battery system but also the deployment of mobile and stationary applications and their behavior during dynamic loads.

Battery systems are modeled and simulated in the different software environments during loading. In this work was explained methods that can be mathematically describe the battery system. The main part of the model is characterized by the creating the battery model in the software MATLAB / Simulink. In the end of the work are presented the results of simulations which can be summarized into these points:

• Nonlinear dynamic battery model in MATLAB / Simulink results given by the values of: voltage, current, capacity and value of the charge during dynamic loading.
• Model can be applied to loads the electric vehicles, mobile applications and stationary applications.
• Model is dependent on the temperature of the rechargeable battery, where the effect of temperature should be impact on the capacity and state of charge.
• Model is ready for integration recuperation management system
• Battery model is possible and appropriate to extend by the hybridization energy system – the connection to the energy system with fuel cell systems and supercapacitors.

Acknowledgement

This work was supported by the Ministry of Defence of the Slovak Republic under contract No. SEOP – 17 – 21 / 2011 – OdPP.

References

1. B. Kennedy, D. Patterson and S. Camilleri, “Use of lithium-ion batteries in electric vehicles”, Journal of Power Sources, vol. 90, pp. 156–162, 2000.
2. Q. Huang, M. Yan and Z. Jiang, “Thermal study on single electrodes in lithium-ion battery”, Journal of Power Sources, vol. 156, pp. 541–546, 2006.
3. D. Ra and K. S. Han, “Used lithium ion rechargeable battery recycling using Etoile-Rebatt technology”, Journal of Power Sources, vol. 163, pp. 284-288, 2006.
4. K. A. Smith, “Electrochemical Modeling, Estimation and Control of Lithium-ion Batteries”, Ph. D. Dissertation, Department of Mechanical Engineering, The Pennsylvania State University, USA, 2006.
5. D. W. Dees, V. Battaglia and A. Belanger, “Electrochemical modeling of lithium polymer batteries”, Journal of Power Sources vol. 110, pp. 310- 320, 2002.
6. P. Rong and M. Pedram, “Dynamic Lithium-Ion Battery Model for System Simulation”, IEEE Transactions on Very Large Scale Integration Systems, vol. 14, pp. 441-451, 2006.
7. A. Hajizadeh and M. A. Golkar, , “Intelligent power management strategy of hybrid distributed generation system”, Int. Journal of Electrical Power and Energy Systems, vol. 24, pp. 783-795, 2007.
8. S. Buller, M. Thele, R. W. D. Doncker and E. Karden, “Impedance based simulation models of supercapacitors and Li-ion batteries for power electronic applications”, IEEE Transactions on Industry Applications, vol. 41, pp. 742-747, 2005.
9. B. Y. Liaw, G. Nagasubramanian, R. G. Jungst and D. H. Doughty, “Modeling of lithium ion cells—A simple equivalent-circuit model approach”, Journal of Solid State Ionics, vol. 175 , pp. 835–839, 2004.
10. M. Chen and G. A. R. Mora, “Accurate electrical battery model capable of predicting runtime and I-V performance”, IEEE Transactions on Energy Conversion, vol. 21, pp. 504-511, 2006.
11. S. C. Chen, C.C. Wan and Y.Y. Wang, “Thermal analysis of lithium-ion batteries”, Journal of Power Sources, vol. 140, pp. 111–124, 2005.
12. D. H. Doughty, P. C. Butler, R. G. Jungst and E. P. Roth, “Lithium battery thermal models”, Journal of Power Sources, vol. 110, pp. 357-363, 2002.
13. R. Spotnitz, “Simulation of capacity fade in lithium-ion batteries”, Journal of Power Sources, vol. 113, pp. 72-80, 2003.
14. P. Ramadass, B. Haran, R. White and B. N. Popov, “Mathematical modeling of the capacity fade of Li-ion cells”, Journal of Power Sources, vol. 123, pp. 230–240, 2003.
15. MATLAB/Simulink Library Help
16. Dennis Doerffel; Soleiman Abu Sharkh, “A Critical Review of Using the Peukert equation for Determining the Remaining Capacity of Lead-acid and Lithium-ion Batteries”, Journal of Power Systems, Vol.155, Issue: 2, p.p. 395-400, April 2006
17. Moore s. ;Ehsani M., “An Empirically based Electrosource Horizon Lead-acid Battery Model”, SAE Transactions, Vol.105, no6, p.p. 421-424, 1996
18. S.Williamson S.; Rimmalapudi C.; Emadi A., “Electrical Modeling of Renewable Energy Sources and Energy Storage Devices”, Journal of Power Electronics, Vol.4, No.2, April 2004
19. Ehsani, M., Gao, Y., Emadi, A. (2010). Modern Elecric, Hybrid Electric and Fuel Cell Vehicles, Fundamentals, theory, and design, Second Edition, CRC Press, boca Raton, Florida, ISBN: 0- 8493-3154-4
20. Min-Joong Kim and Huei Peng, Power Management and Design Optimization of Fuel Cell/Battery Hybrid Vehicles, Journal of Power Sources, Vol.165, issue 2, March 2007, pp.819-832.
21. DHAMEJA,S.: Electric Vehicle Battery Systems, Newnes, USA 2001.

---

Coauthor of this paper is J. Madarás, Institute of Power and Applied Electrical Engineering, Faculty of Electrical Engineering and Information Technology, Slovak University of Technology in Bratislava