Významným poslaním tohto príspevku ukázať ľahkým a zrozumiteľným podaním aspoň jeden nástroj na vytvorenie dobrých vlastnosti riadenia pre viac osí nosič hlavice delenia materiálov (technológiami AWJ, Plazma, kyslíkoacetylenový horák a iné) s cieľom dosahovať čo najlepšiu kvalitu povrchu deleného materiálu, s využitím vlastnosti moderných technológii delenia. Pre dosiahnutie predstavených cieľov využijeme jednu z viacerých možnosti, a to prostriedky neurónových sietí a ich danosti. Na jednoduchej úlohe prakticky ukážeme správanie neurónovej siete a vybrané vzorové realizácie.

Doterajšie riešenia

Úlohy vytvárania riadenia (trajektórii) pre zariadenia nesúce technologické hlavice sú dnes veľmi často riešené v mnohých prácach. Tie majú za cieľ prinášať za stanovených podmienok a ďalších rušivých vplyvov a tiež rôznorodých požiadaviek očakávaný spôsob riadenia. Medzi požiadavky zahrnieme odstránenie, potlačenie tých vplyvov, ktoré znižujú kvalitu realizovanej technológie, za podmienok statických a tiež za situácie premenlivých (dynamických rušivých) procesov. Vytvorenie požadovaného riadenia predpokladáme v reálnom čase [15]. V konkrétnych, špecifických a z rôznych príčin aj nešpecifikovaných porúch v prostredí riadenia je preferované bezkontaktné (bezdotykové) riadenie nesenej technologickej hlavice, príp. predprogramovanie (hrubá šablóna riadenia), ktorú potom mechanický nosič realizuje [9].

Mnohé súčasné práce sa zaoberajú aj aplikáciami v oblastiach robotiky, kde je nutné prekonávať viacero rušivých vplyvov. Niektoré inovačné prístupy plánovania trajektórie sú ťažkopádne a náročné na výpočet najmä v reálnom stave prostredia. Li a Bui [7] navrhovali tekutinový model plánu trajektórie v nemennom prostredí využitím modelu tekutiny, aplikáciou Poissonových rovníc a heuristických princípov. Pre potlačenie kolízií viacosého manipulátora využívajú model (techniku) bitovej mapy. Ong a Gilbert [8] uvádzajú model, ktorý určuje vzdialenosti objektov na platforme možných kolíznych stavov, namiesto hľadania vhodnej, voľnej cesty. Ich algoritmus určuje index prekrytia manipulátora (prípadne iného objektu) a prekážky, pričom za bezpečnú trajektóriu je prijatá tá, ktorá má nulové prekrytie. Možno nájsť tiež stavy, kde postup môžeme doplniť alebo úplne zameniť používané algoritmy vytvárania trajektórie.

Aplikáciou neurónových sietí nájdeme použitie pre modely generujúce trajektóriu v reálnom čase pomocou učenia. Ritter [10] navrhuje Kohonenovu samoorganizujúcu mapu, založenú na neurónových sietiach, na učenie (získanie) transformácie (prevodu) z kartézkeho súradného systému do pracovného priestoru manipulátora. Kinematiku a dynamiku ramena nosiča sa susediace neuróny učia spoluprácou. Fujii [1] navrhuje viacvrstvový model s primeraným algoritmom pre potlačenie kolízií v prostredí (dynamickom) s viacerými manipulátormi a viacerými prekážkami, pričom vytvárané trajektórie nie je optimalizované, najmä v začiatočnej fáze učenia sa.

Choi [6] priniesol algoritmus tvorby trajektórie ramena aplikáciou neurónovej aktivity určujúcej mieru naučenia na báze predchádzajúcich riešení. Neurónová sieť je zložená z dvoch časti – jedna pre riadenie pohybov a druhá pre riadenie statickej polohy. Vstupná vrstva je naučená prepínať medzi týmito sieťami. Veľmi operatívne riešenie možno vidieť pri aplikácii multiagentového systému s implementovaným algoritmom mraveniska, stáda, húfu, kŕdľa, roja, kde v reálnych prírodných kŕdľoch a pri veľmi vysokých rýchlostiach a extrémne rýchlych zmenách prostredia a dynamiky prostredia ku kolíziám nedochádza [11]. Praktický všetky vyššie uvedené možnosti, riešenia a metódy umožňujú do procesu vytvárania riadenia doplniť okrem pohybových premenných aj premenné technologické, premenné majúce vplyv na kvalitu procesu a výrobku. Významným spôsobom zmenia ekonomiku a efektívnosť, tiež náročnosť procesov ak včleníme do riadenia aj energetické, časové, logistické a distribučné parametre.

Pre oblasť technológii delenia sú významné premenné ovplyvňujúce vlastnosti, a tiež potrebné aj pre tvorbu riadenia a tie môžeme spomenúť. Pre kvalitu a presnosť povrchu reznej plochy, pri technológiách (AWJ, Plazma, kyslíkoacetylenový horák a iné) sú to parametre: homogenita prúdu, stabilita, modulácia prúdu, pohyb a rozloženie abrazíva v prúde, orientácia častíc vody a abrazíva, „koherentnosť“, oscilácie pridané k základnému pohybu (priečne, pozdĺžne, tvarové, smerové, kombinované, spojité, impulzné,..) a ďalšie, všetky ktoré vieme pozorovať, merať a ovládať, je dobre zahrnúť ich do identifikácie a pred ich prijatím alebo vylúčením stanoviť veľkosť podielu na zmenu markantných ukazovateľov kvality. Vynechaním ktoréhokoľvek kvalitotvorného parametra, sa hodnota dosahovaných vlastnosti významné znižuje dôsledkom vzájomnej neexistencie prospešných synergii.

Model neurónu

Model neurónu pre činnosti riadenia si možno vybrať z viacerých možnosti a vlastnosti vhodných pre riešenú úlohu. Jedným z možných predstaviteľov je [2], [5] Vychádzajúci z klasických zdrojov o vlastnostiach neurónov, možno prijať ako základ pre vytvorenie modelu neurónovej siete zovšeobecnenú rovnicu (1) s parametrami, ktoré v procese riešenia budeme meniť (nastavovať).

(1)

kde x_i je neurónová aktivita (potenciál) i –tého neurónu, A, B a D nezáporné konštanty reprezentujúce mieru útlmu a hornú a dolnú hranicu neurónovej aktivity, S_i⁺ a S_i^– budiace a tlmiace vstupy neurónu

Štruktúra neurónovej siete

Vlastnosti neurónovej siete stručne priblížime obecnou ilustráciou, a následným popisom jej niektorých vlastnosti. [3]. Na obr. 1. vidíme zovšeobecnenú ilustráciu neurónu s následným modelom (2).

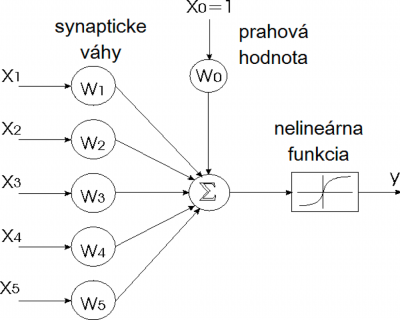
Obr.1. Jednoduchý model neurónu [4]

Matematicky je možné funkciu neurónu popísať:

(2)

kde: x_i – je hodnota na i – tom vstupe, w_i – je váha i – tého vstupu, Θ – je prahová hodnota, n – je celkový počet vstupov, F – je obecná nelineárna funkcia, y – je hodnota výstupu.

Zoskupením jednotlivých neurónov do siete v závislosti od sledovanej úlohy a jej funkčnej štruktúry vytvárame sieť s požadovanými vlastnosťami a potrebnými reakciami.

Umelá neurónová sieť

Je zrejme jeden neurón má pomerne jednoduchú funkčnosť, nie je v jeho silách realizovať zložitejšie činnosti. Sila neurónovej siete je v zoskupení umelých neurónov, do sieti, štruktúr podmienených riešenou úlohou. Od zložitosti úlohy je závislá aj štruktúra a početnosť siete. Umelá neurónová sieť je vlastne deterministické zoskupenie a prepojenie jednoduchých neurónov (prvkov siete). Možnosti štruktúrovania a zložitosti je možné realizovať s vysokou flexibilitou a potrebnou spoľahlivosťou.

Pri zostavovaní štruktúry siete je možné ľubovoľne prepájať vstupy a výstupy neurónov, preferovať, alebo potlačiť, prípadne utlmiť vybrané vstupy (aktivity), minimalizovať vplyv nekorektne, alebo (koalične resp. opozične) správajúceho sa neurónu vo vzťahu k celkovému výsledku. Samozrejme aj tento prístup má svoje nedostatky. Najviac ťažkosti sa vyskytuje pri modelovaní zložitých a veľmi zložitých štruktúr, kde niektoré prepojenia medzi neurónmi je komplikovaná situácia. Tiež môžeme spomenúť výskyt nejednoznačnosti a viacznačnosti pri zostavovaní zložitých štruktúr.

Vnútorná štruktúra neurónovej siete a jej vrstvy

Z hľadiska syntézy je najčastejšie využívaná viac vrstvová štruktúra neurónovej siete, ukázané na obr. 2. Výstupy z i – tej vrstvy sú privedené na vstupy vo vrstve i+1. Prvú vrstvu označujeme ako vstupná alebo rozdeľovacia vrstva a jej úlohou je prijímať hodnoty z okolia, spracovať ich a výstupy priviesť na vstup každého neurónu nasledujúcej vrstvy. Poslednú vrstvu nazývame výstupná alebo akčná a hodnoty na jej výstupoch sú odozvou (reakciou) celej siete na vstupné vzorky. Vnútorné vrstvy obvykle nazývame skryté vrstvy. Počet vrstiev a počet neurónov v jednotlivých vrstvách sú závisle na zložitosti funkcie, ktorú od siete vyžadujeme.

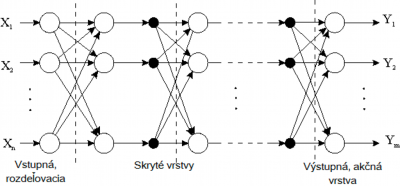
Obr.2 Viac vrstvová štruktúra neurónovej siete [4]

Pridaním potrebných vlastnosti neurónových prvkov, máme predpoklady pokračovať pri vytváraní modelu.

Algoritmus modelu

Rovnicu (1) môžeme vzhľadom na prostredie neurónu a polaritu vstupných neurónových signálov upraviť nasledovne [15 (Yang, 2001)]

(3)

kde N – celkový počet neurónov v neurónovej sieti, – budiace a tlmiace vstupy, I_i – externý vstup do i – tého neurónu, definovaného ako:

(4)

Matica váh prepojení medzi neurónom i a j je symetrická a definovaná ako

(5)

Premenná d_ij predstavuje Euklidovu vzdialenosť medzi neurónom i a j v stavovom priestore S. Každý neurón má prepojenie len v ohraničenom priestore s najbližšími neurónmi a nie s celým počtom neurónov N. Susedstvo neurónu býva najčastejšie k = 2.

Modelovanie procesov neurónovej siete

V uvažovanej úlohe skúmame viacosí pracovný priestor manipulačného prostriedku, ktorý pre našu úlohu predstavuje nosič technologického nástroja nad pracovnou plochou. Neurónová sieť vytvára riadenie s požadovanými vlastnosťami. Pre našu úlohu použijeme sieť 22×24 neurónov zoradených v pravouhlej štruktúre, neuróny majú prepojenia so susediacimi. Funkcia cieľového neurónu na celú sieť je vyjadrená aktivitou každého neurónu na najbližšie okolie a váhovými koeficientmi medzi susediacimi neurónmi.

Hľadaná trajektória, ak taká existuje, je použiteľná (najvhodnejšia, optimalizovaná,…) vzhľadom na požadované vlastnosti riadenia. Pre učenie siete boli zvolené viaceré kombinácie parametrov (A, B, D, E), Parametre v ďalšom skúmaní bude potrebné podrobiť vhodnejšiemu nastaveniu a dôkladnému procesu optimalizácie. Činnosť neurónov naučenej siete v stabilnom prostredí zobrazuje obr. 2. Prepojenia cieľových neurónov mení aktivitu okolitých neurónov, pričom veľkosť okolia neurónu je vybraná ako k = 2. Činnosť vyjadrujúca vplyvy neurónov je nastavená nasledovným spôsobom

(6)

kde a je definované ako

(7)

i – počet neurónov patriacich okoliu.

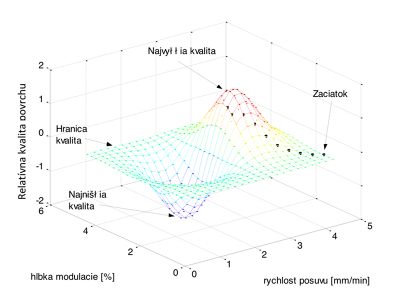
Obr. 3. Aktivita neurónov a vytvorené riadenie v statickom prostredí

Aby mohlo byť nájdené riadenie v súlade s požadovanými vlastnosťami, je potrebné, aby sa stavy riadenia nachádzali v miestach čo najnižšej úrovne nežiaducich vplyvov na kvalitu vykonávanej technológie. Záporná aktivita neurónov pamätajúcich si stavy nevhodných vlastnosti, nemôže ovplyvniť okolité neuróny, aby sa informácia o nežiaducej kvalite technológie nešírila do susediacich neurónov, cez ktoré sa riadenie technológie (manipulátor) nebude pohybovať. Nájdené stavy riadenia sú znázornené na obr. 3 predstavujú jedno z možných riešení vzhľadom na požadované vlastnosti technológie. Hodnoty stavov riadenia a aktivít cieľového neurónu sa vďaka prepojeniu neurónov šíri po celej sieti a vyhľadáva neuróny, kde je hodnota tejto informácie na najvyššej hladine. Ak je aktuálna pozícia p_a, tak nasledujúca pozícia p_n je určená výberom

(8)

k – určuje počet susediacich neurónov k neurónu s polohou p_a.

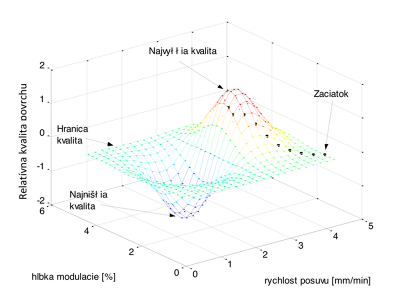
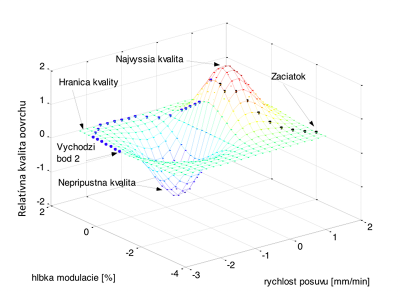
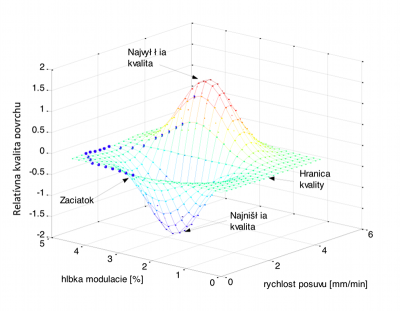
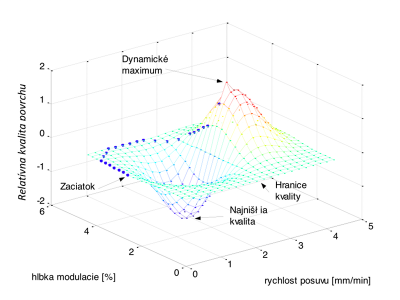
Obr. 4 Aktivita neurónov a vytvorené riadenie v dynamickom prostredí

Ak susediace neuróny nemajú vyššiu aktivitu, aktuálna pozícia zostava nezmenená a riadenie technológie sa nemení. Vo vzťahu (3) sa aktivita zvyšuje intenzitou danou výrazom Pri rovnakom vstupe sa aktivita x_i zvyšuje tým menej, čím je x_i bližšie ku x_i. Ak x_i <B, budiaci vzťah je pozitívny a x_i sa zvyšuje. Ak x_i = B, aktivita sa nezvyšuje, ak x_i > B, potom je aktivita potláčaná naspäť k hodnote B. Aktivita neurónu sa teda pohybuje v úzkom intervale hodnôt okolo B. Podobne to platí aj s hodnotou D, ktorá určuje dolnú hranicu aktivity. Ak sa aktivita x_i nachádza v intervale hodnôt , je zaručené, že zostane v tomto intervale pre ľubovoľné hodnoty budiacich a tlmiacich signálov.

Stabilita a smerovanie navrhnutého modelu sa dá overiť tiež pomocou Ljapunovej teórie stability [15]. Pre dynamickú simuláciu s premenlivými vlastnosťami procesu (cieľom) sa aktivita neurónov mení spolu s vlastnosťami technológie a vytvárané riadenie má tvar hladkých funkcii. Významným parametrom je tu relatívna rýchlosť zmeny vlastnosti prostredia a prebiehajúceho technologického procesu (cieľ vytváraného riadenia). Ak zmeny vlastnosti technológie prebiehajú pomalšie ako reakcie neurónovej siete potom je situácia vhodná pre reálne nájdenie dobrých výsledkov sledovanej požadovaných vlastnisti procesu. Pre prípad, že generované riadenie je pomalšie ako zmena dynamického prostredia, potom vytvárané riadenie nevie dosiahnuť požadovaných vlastnosti, a je nutne efektívnejšie stabilizovať technológiu a tým vytvoriť podmienky dosiahnutia požadovaných vlastnosti. Aktivita neurónov pre dynamický premenlivé prostredie technológie je znázornená na obr. 4.

Zmena vlastnosti technológie a prostredia mení aktivitu neurónov vzhľadom na svoju aktuálnu hodnotu požadovanej veličiny. Avšak len samotný aktuálny cieľový neurón mal najvyššiu možnú aktivitu x_i = 1. Generovanie nasledujúceho stavu riadenia pn je ovplyvňované aktuálnym stavom, tak informácia o ňom je šírená cez matice váh do celej siete. To má za následok, že vytvárané riadenie sa nemusí javiť ako najlepšie (optimalizované, optimálne, efektívne,…), ak sa zoberie do úvahy len výsledný statický stav, keď sa vlastnosti prostredia a technológie nemenia, čo v reálnej technológii delenia vodou, plazmou, plameňom … v praxi nikdy nenastáva. V čase vytvárania riadenia nasledujúceho stavu je však jeho výber určovaný vzťahom (8).

Uvedený príklad je realizovaný pre dvojicu parametrov, s experimentálnou funkciou závislosti kvality na polohe parametrov v priestore riadenia. Úlohu je možné aplikovať na ľubovoľný počet parametrov a tiež ľubovoľný počet vstupných veličín pre činnosť neurónovej siete. Samostatnou analýzou je možne zostavovať a zostaviť vhodnú štruktúru a vybrať efektívne veličiny vstupov z reálneho prostredia. V prípadoch ohraničenej oblasti siete dochádza v začiatočných štádiách učenia sa, k pohybu na hranici oblasti, a aj opakovane sa môže dotknúť hranice. Táto situácia je tiež priestorom na zváženie a vhodnú voľbu veľkosti rozsahu a počtov neurónov v sieti.

Záver

Riadenie procesu vytvárané použitím techniky neurónových sietí a samoučenia sa, je ponúkaný nástroj, ktorý dovoľuje dosiahnuť prijateľné riadenie za podmienok premenlivých zmien v prostredí a technológii. Skúmané statické a dynamické prostredie s požiadavkou vytvárať požadované riadenie v prostredí premenlivých vlastnosti technológii je ukážkou možnosti aplikovať aj v ďalších prípadoch. Správanie sa zvolenej neurónovej siete v podobných elementárnych úlohách je možne upravovať podľa konkrétnych požiadaviek. V súčasnosti existuje mnoho rozpracovaných teórií pre rôzne typy a druhy neurónových sietí, vhodných aj pre popisovanú úlohu. Uvedenú úlohu s drobnými úpravami popísaného algoritmu je možné použiť nie iba pre vzorové úlohy. Prípady nájdenia optimálnych riadení v štádiu učenia sa, či už s učiteľom alebo bez učiteľa [14]. V štádiu testovania je možné navrhnúť vlastnosti riadenia aj pre nenaučené vstupné parametre.

Pre dosiahnutie optimálnych riešení riadení je pre každú konkrétnu úlohu potrebné vykonať analýzu kompletného reťazca od fyzikálneho snímania, úpravy, transformácie, digitalizácie, spracovania pracovných a rušivých veličín technológie, výberu vhodného typu neurónovej siete a zabezpečenie nevyhnutných vlastnosti optimalizácie jednotlivých členov riadiaceho reťazca, a tak vytvoriť predpoklady uspokojivých výsledkov.

Literatúra

1. FUJII, T.: 1998. Multilayered reinforcement learning for complicated collision avoidance problems. In. Proceedings of IEEE international conference on Robotics and Automation, Leuven, Belgicko, 16.–20. máj 1998. s. 2186–2191. ISBN 0-7803-4300-X
2. HODGKIN, A. L., HUXLEY, A. F.: 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. In Journal of physiology, 1952, č. 117 (4), s. 500–544. ISSN 1469-7793
3. http://pldocs.docdat.com/docs/index-162639.html?page=9
4. http://www.elektrorevue.cz/clanky/00013/index.html
5. http://www.fi.muni.cz/usr/jkucera/pv109/2000/xneudert.html
6. CHOI, K. a kol.: 2009. Prediction of arm trajectory from the neural activities of the primary motor cortex with modular connectionist architecture. In Neural Networks, 2009, roč. 22, č. 9, s. 1214-1223. ISSN 0893-6080
7. LI, Z. X., BUI, T. D.: 1998. Robot path planning using fluid model. In. Journal of Intelligent and Robotic Systems, 1998, roč. 21, zv. 1, s. 29–50. ISSN 0921-0296
8. ONG, C. J., GILBERT, E. G.: 1998. Robot Path planning with penetration growth distance, In. Journal of robotics systems, 1998, roč. 15, zv. 2, s. 57–74. ISSN 1097-4563
9. PETRÁŠ, R., ŠURIANSKY, J.: 2011. Mikroroboty v environmentálnej technike. In. Informatika a automatizácia v riadení procesov, VII. vedecká konferencia s medzinárodnou účasťou, Zvolen, 13. október 2011. Zvolen: Vydavateľstvo TU vo Zvolene, 2011, s. 43–49. ISBN 978-80- 228-2267-1
10. RITTER, H. J.: 1989. Topology-conserving maps for learning visuo-motor-coordination. In. Neural Networks, 1989, roč. 2, zv. 3, s. 159–189. ISSN 0893-6080
11. Šebej, Peter: Analýza metód a úloh rozhodovacích procesov s aplikáciou distribuovaných prostriedkov, Bratislava 2005. 144 + 60 s. príl.
12. Šebej, Peter: Evolučný algoritmus a jeho aplikácia na riešenie vybranej úlohy, In: AD&M, Inteligentní systémy pro praxi, predikce, optimalizace, simulace, modelovaní, pravidlové expertní systémy, statistické metódy, fuzzy logika, neuronové sítě, genetické algoritmy, 2004, Seč, ISBN 80-239-3680-8
13. Šebej, Peter: Možnosti využitia neparametrických štatistických testov na evaluáciu tendencie hodnoteného procesu, 2005.In: Aplimat. Part 2. – Bratislava : STU, 2005 S. 537-543. – ISBN 809692642X
14. ŠIPOŠ, Ľ., CSONGRÁDY, T.: 2006. Umelá inteligencia. Zvolen: Vydavateľstvo TU vo Zvolene, 2006, 99 s. ISBN 80-228-1591-8
15. YANG, S. X., MENG, M.: 2001. Neural Network Approaches to Dynamic Collision-Free Trajectory Generation. In. IEEE Transaction on Systems, Man, and Cybernetics – part B: Cybernetics, 2001, roč. 31, zv. 3, s. 302–318. ISSN 1083-4419

---

Katedra manažmentu výroby, Fakulta výrobných technológií v Prešove, Technická univerzita v Košiciach