Matematická morfológia vychádza z vlastností bodových množín a najčastejšie sa aplikuje na binárne obrazy, ale ľahko je ju možné zovšeobecniť aj na šedotónové a farebné obrazy [1], [2]. Morfologické operácie sa teda používajú pri predspracovaní obrazov (zjednodušenie tvaru objektov, odstránenie šumu), zdôraznenie štruktúry objektov (stenčovanie, zhrubnutie, skelet, označovanie objektov), ako aj pre popis objektov číselnými charakteristikami (plocha, obvod, atď.) [3].

Morfologické spracovanie obrazov tak nadobúda významnú úlohu, či už v robotike (napr. rozpoznanie a uchopenie predmetu robotom), automobilovom priemysle (napr. rozvoj technológii detekujúcich objekty na vozovke), medicíne (napr. použitím morfologických filtrov sa dajú zvýrazniť či potlačiť určité objekty na požadovaných snímkach) a v mnohých iných oblastiach. Morfologická filtrácia je v článku prezentovaná v morfologickom spracovaní binárnych obrazov, bližšie špecifikuje vplyv výberu určitých typov štruktúrnych elementov na binárny obraz.

Úvod

Morfologická filtrácia či morfologické spracovanie obrazov pracuje so základnými operáciami množín [4]. Výhodou morfologických filtrov voči lineárnym filtrom je priamy vplyv na tvar či veľkosť objektov v danom obraze. Morfologické filtre vynikajú schopnosťou selekcie podľa jasu a veľkosti objektov v obraze. Ďalšou výhodou implementácie morfologických filtrov v bežnom použití je ich jednoduchosť, pretože nevyžadujú zložité matematické operácie. Morfologické filtre sú úspešne aplikované v systémoch s pevnou rádovou čiarkou. Tieto filtre sú význačné tým, že zachovávajú hrany objektov. To je významný rozdiel voči filtrácii lineárnymi filtrami, po aplikovaní ktorých sú hrany nachádzajúce sa na obraze značne rozmazané [5]. Na základe teoretických podkladov sme previedli realizácie morfologických filtrov v programovom prostredí Matlab. V tomto prostredí boli vytvorené základné morfologické filtre, ako aj ich rozšírené verzie. Záverom tohto článku sa venujeme vlastnostiam jednotlivých morfologických filtrov a ich možnostiach praktického využitia v praxi.

1. Binárna morfológia

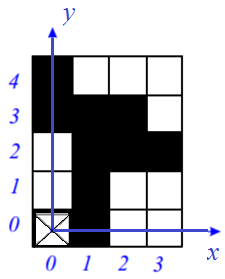
Pre binárnu matematickú morfológiu pracujúcu s dvojrozmerným (2D) obrazom je základným stavebným prvkom dvojica celých čísel (∈Z²). Na binárne obrazy sa môžeme pozerať ako na podmnožinu 2D priestoru všetkých celých čísel Z² a s oborom hodnôt {0, 1}. Obrazový bod (pixel) je reprezentovaný dvojicou celých čísel vzhľadom k dvom súradnicovým osiam diskrétneho rastra (štvorcová mriežka) obrazu. Jednotková dĺžka pozdĺž osí zodpovedá perióde vzorkovania. Binárny obraz je teda možné vyjadriť ako 2D bodovú množinu. Body objektov v obraze reprezentujú množinu A, čomu zodpovedajú obrazové body s hodnotou 1. Body doplnku Ac opisujú pozadie a sú reprezentované obrazovými bodmi s hodnotou 0. Začiatok obrazu má súradnice (0,0). Súradnice ostatných obrazových bodov (x,y) majú rovnaký význam, ako je obvyklé v matematických pravidlách, pričom x označuje stĺpec a y riadok v štvorcovom rastri obrazu. Na Obr. 1 je znázornená ukážka bodovej množiny (obrazu). Body diskrétneho objektu tvoria bodovú množinu K = {(1,0), (1,1), (1,2), (2,2), (3,2), (0,3), (1,3), (2,3), (0,4)} vzhľadom k počiatku (0,0) – ľavý dolný roh.

Obr.1 Ukážka bodovej množiny.

Morfologická operácia je relácia obrazu (bodovej množiny A) s inou, menšou bodovou množinou B. Táto bodová množina B sa nazýva štruktúrny element (structuring element). Štruktúrny element sa vzťahuje k „lokálnemu“ začiatku O elementu, ktorý sa nazýva reprezentatívny bod. Na Obr.2 sú znázornené najčastejšie využívané štruktúrne elementy, pričom reprezentatívny bod O sa nachádza v ich strede (čierny bod) [6].

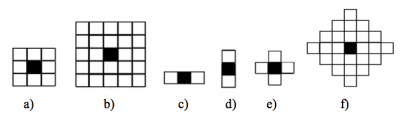
Obr.2 Niektoré štruktúrne elementy.

Popis štruktúrnych elementov:

• a) štvorec veľkosti 3×3 op (obrazový prvok)
• b) štvorec veľkosti 5x5op
• c) horizontálna čiara veľkosti 3x1op
• d) vertikálna čiara veľkosti 1×3 op
• e) kríž veľkosti 1 op od reprezentatívneho bodu v kolmom smere
• f) diamant so šírkou 3 op od reprezentatívneho bodu.

Štruktúrne elementy, ktoré majú rovnaké vlastnosti pre rôzne smery, nazývame izotropické. Aplikácia morfologickej operácie Ψ(A) na obraz A si predstavíme tak, že vybraným štruktúrnym elementom B sa systematicky posúvame po danom obraze a vyhodnocujeme odozvu podľa typu operácie. Výsledok tejto operácie medzi vstupným obrazom A a štruktúrnym elementom B sa zapíše do výstupného obrazu C v reprezentatívnom bode (t.j. buď 1 alebo 0). Erózia a dilatácia sú základné operácie pre morfologickú filtráciu obrazov. Väčšina z ďalej spomínaných algoritmov je založená na kombinácii práve týchto dvoch operácií.

2. Dilatácia

Medzi základné operácie matematickej morfológie patrí dilatácia. Pri dilatácii postupne prechádzame štruktúrnym elementom po vstupnom obraze zľava doprava a zhora dole, pričom sa vyhodnocuje najväčšia hodnotu jasu z op obsiahnutých plochou štruktúrneho elementu, tj. v binárnom prípade hodnota 1. Táto hodnota sa zapíše do aktuálnej polohy op, do tzv. reprezentatívneho bodu už výsledného obrazu C. Dilatácia je používaná pre zaplnenie malých dier a úzkych „zálivov“ medzi objektmi. Jednoducho povedané, pri dilatácii sa objekty v binárnych obrazoch zväčšujú na úkor pozadia. Ak má byť zachovaná veľkosť, potom sa dilatácia kombinuje s eróziou, viď ďalej. Operácia dilatácia je komutatívna, asociatívna a invariantná voči posunutiu. Vlastnosti, ako šírka a veľkosť zmeny objektu, sú kontrolované štruktúrnym elementom [2], [7], [8]. Dilatácia obrazu A elementom B je matematicky zapísaná ako

(1)

Na Obr.3 je znázornený postup procesu dilatácie vstupného čierno-bieleho obrazu, ktorý je kvôli názornosti zapísaný v binárnej forme, štruktúrnym elementom tvaru štvorca veľkosti 3×3 op (Obr.2a). Objektom v obraze je biely štvorec v jeho strede, Obr.3a) . Začiatok procesu dilatácie začína umiestnením reprezentatívneho bodu štruktúrneho elementu do ľavého horného rohu obrazu. Tie op elementu, ktoré prekračujú rozsah obrazu, sa procesu vyhodnocovania operácie dilatácie nezúčastňujú. Na Obr.3b je znázornená situácia, kedy sa štruktúrny element prvý krát prekryje svojim dolným pravým rohom (červene) s objektom v obraze (dovtedy pri posune štruktúrneho elementu a jeho interakcii s pozadím obrazu nenastala žiadna zmena).

Reprezentatívny bod O v strede štruktúrneho elementu je na obrázku ohraničený čiernym štvorčekom a pozadie obrazu bolo vynechané kvôli názornosti. Pri dilatácii sa vyhodnotí v tejto situácii najvyššia hodnota op v celom štruktúrnom elemente, t.j. 1 a tá sa zapíše do pozície reprezentatívneho bodu vo výslednom obraze. Operácie dilatácie vstupného obrazu je ukončená, keď reprezentatívny bod elementu sa prekryje s posledným op vstupného obrazu. Výsledný obraz po ukončení procesu dilatácie je na Obr.3c, kde je vidieť, že došlo k zväčšeniu objektu o jeden riadok a jeden stĺpec z každej strany, čo naznačujú aj čierne šípky v jeho rohoch.

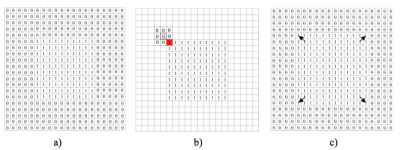
Obr.3 Ukážka procesu dilatácie: a) vstupný obraz, b) prvé prekrytie štruktúrneho elementu s objektom v obraze, c) dilatovaný obraz.

3. Erózia

Pri erózii, rovnako ako pri dilatácii, je zmena hodnoty op v obraze určená štruktúrnym elementom. Avšak pri erózii sa vyhodnocuje najmenšia hodnotu jasu z op obsiahnutých štruktúrnym elementom (t.j. hodnota 0) a táto hodnota sa potom zapíše do aktuálnej polohy reprezentatívneho bodu výsledného obrazu. Zjednodušene povedané, erózia zmenšuje objekty a objekty menšie ako štruktúrny element odstráni. Erózia sa používa k zjednodušeniu štruktúry (rozloženiu objektu na jednoduchšie časti). Erózia je duálna transformácia k dilatácii, nie inverzná. Erózia nie je komutatívna, ale je invariantná voči posunutiu [2], [7], [8]. Erózia obrazu A elementom B je matematicky zapísaná ako

(2)

Odčítaním erodovaného a vstupného obrazu môžeme získať obrysy objektov v obraze.

4. Otvorenie a zatvorenie

Erózia nasledovaná dilatáciou vytvára ďalšiu morfologickú operáciu nazývanú otvorenie. Otvorenie vyhladzuje obrysy objektov, odstraňuje malé objekty a prerušuje tenké „úžiny“ medzi blízkymi objektami, pričom miera mazania, či prerušenia je daná veľkosťou a tvarom štruktúrneho elementu [2], [8]. Otvorenie množiny A štruktúrnym elementom B sa označuje A∘B a je definované ako

(3)

A∘B je zjednotením všetkých posunov štruktúrneho elementu B, ktoré vošli do štruktúry objektu A vstupného obrazu . Postup operácie otvorenia spôsobujúceho vyhladenie obrysov objektu je znázornený na Obr.4, pre názornosť na spojitom obraze [3], [4].

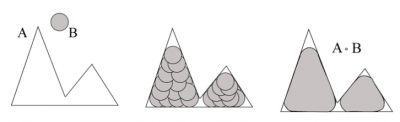
Obr. 4 Vstupná množina A a štruktúrny element B (vľavo), pohyb štruktúrneho elementu objektom (v strede), výsledok otvorenia – zjednotenie plochy pohybu štruktúrneho elementu (vpravo).

Štruktúrny element B na Obr. 4 má tvar kruhu a objekt A má špicatý tvar. Vo výslednom obraze (vpravo) tenká čiara ohraničuje pôvodný obrys objektu. Biela plocha pod ňou je priestor, kde sa štruktúrny element nedostal a šedá plocha je výsledok otvorenia. Vidno, že tvar objektu sa zmenil, rozdelil sa na dva menšie objekty. Je zrejmé, že veľkosť a tvar štruktúrneho elementu ovplyvňuje jemnosť výsledných detailov v obraze. Ďalšou morfologickou operáciou je zatvorenie. Je definované, ako dilatácia nasledovaná eróziou. Zatvorenie množiny A štruktúrnym elementom B sa označuje A∙B a je definované ako

(4)

Zatvorenie tiež vyhladí obrysy objektov tým, že zaplní malé okrajové trhliny, zaplní malé diery v objektoch a tiež môže spojiť blízke objekty, medzi ktorými je úzky „záliv“. Všetko to znova závisí od veľkosti a tvaru štruktúrneho elementu. Podobne, ako v predchádzajúcom prípade, je na Obr.5 zobrazený postup operácie zatvorenia [3], pričom vstupný objekt A, ako aj štruktúrny element B sú rovnaké.

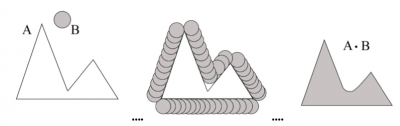
Obr. 5 Vstupný objekt A a štruktúrny element B (vľavo), pohyb štruktúrneho elementu opisujúci objekt z vonku ( v strede), výsledok operácie zatvorenia (vpravo).

Na výslednom obrázku operácie zatvorenia (Obr.5 vpravo) sa nenachádzajú nevyplnené oblasti vstupného objektu, ako to bolo pri otvorení. Práve naopak, zatvorenie vypĺňa vonkajšie ostré plochy doplnkom k opísanej ploche štruktúrneho elementu. Tak ako otvorenie, aj morfologické zatvorenie zjemňuje obrysy vstupného objektu. Vypĺňa diery menšie ako štruktúrny element, spája menšie prerušenia a zarovnáva malé vypukliny. Výsledkom operácii otvorenia a zatvorenia je teda zjednodušený obraz s menším počtom detailov. Obe tieto operácie sa používajú pri morfologickom filtrovaní obrazu. Otvorenie a zatvorenie sú duálne morfologické operácie. Ďalšou vlastnosťou otvorenia a zatvorenia je idempotentnosť, čo znamená, že ich opakovaná aplikácia nemení predchádzajúci výsledok [3].

5. Výsledky simulácie a ich zhodnotenie

Programové prostriedky na implementáciu vybraných algoritmov morfologickej filtrácie boli vytvorené v programe Matlab [4], [5]. Umožňujú pracovať jednak s predefinovanými obrazmi, ktoré boli vybrané tak, aby čo najlepšie demonštrovali možnosti morfologických filtrov. Program umožňuje načítanie aj iných, ako predvolených obrazov typu jpeg, bmp, gif. Maximálna veľkosť spracovaného obrazu je do 1000×1000 op. Ďalej umožňuje výber typu morfologickej operácie, výber rôznych typov štruktúrnych elementov (Obr.2), ako aj výber ich veľkosti. Užívateľské rozhranie umožňuje zobraziť vstupný obraz a výstupný obraz po morfologickej filtrácii, histogramy vstupného a výstupného obrazu. Pri reprezentácii výsledkov v tomto článku sme sa sústredili na poukázanie vplyvu výberu rôznych typov štruktúrnych elementov pri morfologickej filtrácii binárnych obrazov. Ako vstupný obraz sme na ukážku vybrali rôzne poškodený biely text (objekty) na čiernom pozadí, ktorý je zobrazený na Obr.6.

Obr.6 Vstupný binárny obraz.

Na Obr.7 je zobrazená morfologická dilatácia tohto obrazu s rôznymi typmi štruktúrneho elementu. Vo všetkých prípadoch došlo podľa očakávania k zaplneniu malých dier (poškodení) v jednotlivých písmenách (objektoch), ako aj k ich zväčšeniu. Pri voľbe veľkosti vybraných štruktúrnych elementov sa zohľadnila veľkosť písmen v obraze. Na Obr.7a) bol použitý štruktúrny element tvaru horizontálnej čiary veľkosti 3×1 op (z obr. 2c) a na vedľajšom Obr.7b) zase element tvaru vertikálnej čiary veľkosti 1×3 op (Obr.2d). Z porovnania týchto dvoch výsledných obrazov vidno, že vizuálne vyššia kvalita sa dosiahla pri použití elementu tvaru vertikálnej čiary, čo súvisí s charakterom tvaru písmen.

Obr.7 Morfologická dilatácia vstupného obrazu so štruktúrnym elementom typu: a) horizontálna čiara veľkosti 3x1op, b) vertikálna čiara veľkosti 1×3 op, c) diamant so šírkou 2 op od reprezentatívneho bodu, d) kríž veľkosti 1 op v kolmých smeroch, e) štvorec veľkosti 3×3 op.

Na Obr.7c) vidíme výsledok dilatácie pri použití štruktúrneho elementu tvaru diamant so šírkou 2 op od reprezentatívneho bodu (od jeho stredu). Tento typ elementu sa ukázal ako najmenej vhodný na dilatáciu pri tomto charaktere obrazu, pretože zväčšil veľkosť písmen tak, že na mnohých miestach došlo k „zliatiu“ písmen a napr. slová ako školská taška sú takmer nečitateľné. Tento element vykazoval najhoršie výsledky aj pri ďalších morfologických operáciách. Obr. 7d) zobrazuje výsledok dilatácie so štruktúrnym elementom typu kríž veľkosti 1 op v kolmých smeroch (Obr.2e). Všetky písmena sú čitateľné, avšak oproti Obr.7b) pôsobia roztraseným dojmom. Pri obraze na Obr. 7e), kde bol použitý element tvaru štvorca veľkosti 3×3 op , vidíme celkom dobrý výsledok dilatácie, s odstránenými poškodeniami v písmenách, ale v slove „školská“ došlo tiež k väčšiemu prepojeniu písmen navzájom. Zo všetkých piatich uvedených obrazoch zobrazujúcich dilatáciu vyšiel najlepšie Obr. 7b), pri ktorom bol použitý štruktúrny element typu vertikálna čiara veľkosti 1×3 op.

Obr.8 Morfolofická erózia vstupného obrazu so štruktúrnym elementom typu: a) horizontálna čiara veľkosti 3x1op, b) vertikálna čiara veľkosti 1×3 op, c) diamant so šírkou 2 op od reprezentatívneho bodu, d) kríž veľkosti 1 op v kolmých smeroch, e) štvorec veľkosti 3×3 op.

Ako bolo vyššie uvedené, erózia zmenšuje objekty a odstraňuje objekty menšie ako štruktúrny element Na Obr. 8, kde je zobrazená erózia vstupného obrazu (Obr.6) s rôznymi typmi štruktúrneho elementu, môžeme vidieť, že pre tento tvar vstupného obrazu samostatná operácia erózie nie je vhodná. Vo všetkých prípadoch došlo k zhoršeniu kvality obrazu a pri použití elementu diamant so šírkou 2 op od reprezentatívneho bodu boli odstránené všetky písmená, zostali z nich iba 2 biele op (Obr. 8c), pričom výber menšej veľkosti tohto typu elementu už nie je možný. Obr.8d) a Obr.8c) stratili po erózii čitateľnosť textu v obraze. Z porovnania týchto piatich výsledných obrazov po erózii môžeme konštatovať, že najlepšiu čitateľnosť, aj napriek väčšiemu poškodeniu, dosahuje Obr.8a), kde bol požitý element typu horizontálna čiara veľkosti 3x1op.

Obr.9 Morfologické otvorenie vstupného obrazu štruktúrnym elementom a) horizontálna čiara veľkosti 3x1op, b) vertikálna čiara veľkosti 1×3 op, c) diamant so šírkou 2 op od reprezentatívneho bodu, d) kríž veľkosti 1 op v kolmých smeroch, e) štvorec veľkosti 3×3 op.

Na Obr. 9 sú zobrazené výsledky pre morfologickú operáciu otvorenie. Keďže otvorenie je erózia nasledovaná dilatáciou, tak tam, kde došlo k veľkému odstráneniu bielych op po erózii, tak následná dilatácia už nemohla pridaním bielych op „opraviť“ písmená v texte obrazu. Na Obr. 9c) zostali dva spomínané body, ktoré iba zväčšili svoj objem oproti Obr.8c) a na Obr.9e) zostal text naďalej úplne nečitateľný. Zo zvyšných troch výstupných obrazov dosiahol najlepšie výsledky (čitateľnosť) Obr.9a). Pri ňom sa dá konštatovať, že vylepšil výsledok z Obr.8a), avšak nedosahuje ani úroveň kvality vstupného obrazu (Obr.6).

Ako posledná morfologická operácia na danom vstupnom obraze bola odsimulovaná operácia zatvorenie a jej výsledky sú zobrazené na Obr.10. Vo všetkých prípadoch je text čitateľný, došlo k odstráneniu poškodení v texte vstupného obrazu. Najhorší výsledok bol znova pri použití štruktúrneho elementu typu diamant so šírkou 2 op od reprezentatívneho bodu (Obr. 10c). Na tomto obrázku došlo na viacerých miestach k zliatiu bielej farby (prepojenie objektov). Zo zvyšných štyroch výstupov po zatvorení vykazuje trochu horšiu kvalitu Obr.10e), kde bol použitý element typu štvorec veľkosti 3×3 op. Avšak pri jeho porovnaní s Obr. 7e) môžeme konštatovať, že použitie operácie zatvorenia na tento tvar vstupného obrazu je vhodnejšie, ako iba operácie dilatácie, ak sa použije spomínaný element typu štvorec veľkosti 3×3 op. Najlepší výsledok zatvorenia sa dosiahol pri elemente vertikálna čiara veľkosti 1×3 op.

Obr.10 Morfologické zatvorenie vstupného obrazu štruktúrnym elementom a) horizontálna čiara veľkosti 3x1op, b) vertikálna čiara veľkosti 1×3 op, c) diamant so šírkou 2 op od reprezentatívneho bodu, d) kríž veľkosti 1 op v kolmých smeroch, e) štvorec veľkosti 3×3 op.

Na Obr.11 je porovnanie vstupného obrazu (vľavo) s najlepšími dosiahnutými výsledkami pri binárnej morfologickej filtrácii a to po dilatácii (v strede) a po zatvorení (vpravo). Z porovnania vyplýva, že pri subjektívnom zhodnotení sa javí operácia zatvorenie so štruktúrnym elementom vertikálna čiara veľkosti 1×3 op ako najvhodnejšia pri tomto type vstupného testovaného obrazu.

Obr.11 Vzájomné porovnanie vstupného obrazu (vľavo), jeho dilatácie (v strede) a zatvorenia (vpravo).

Záver

Článok bol zameraný na popis a simuláciu vybraných morfologických filtrácii pri spracovaní binárnych obrazov. Erózia a dilatácia sú základnými operáciami matematickej morfológie a ďalšie operácie, ako otvorenie zatvorenie, sú akousi „nadstavbou“ vytvorenou kombináciou erózie a dilatácie. Zamerali sme sa na vplyv výberu rôznych typov štruktúrneho elementu na daný typ vstupného obrazu. Veľkosť a tvar štruktúrneho elementu ovplyvňuje jemnosť výsledných detailov v obraze. Objekty v obraze tvorili rôzne poškodené písmena v textoch a cieľom bolo získať pomocou morfologickej filtrácie opravu týchto poškodení. Pre tento typ vstupného obrazu sme dosiahli najlepšie výsledky pri operácii zatvorenie so štruktúrnym elementom vertikálna čiara veľkosti 1 x 3 obrazové prvky, čo súvisí aj s charakterom tvaru písmen.

Morfologická filtrácia spracovaná v tomto článku je len malou ukážkou možnosti spracovania obrazu pomocou matematickej morfológie. Tieto metódy majú široké uplatnenie v oblasti spracovania obrazu od medicíny, stavebníctva, detekcie objektov, až po spracovanie snímok z vesmíru. Užitočnou súčasťou morfologických filtrov je ich nadstavbová časť tzv. morfologická segmentácia [9]. Táto technika v sebe spája spomínané filtre a dopĺňa ich o radu ďalších aplikácií. Touto cestou vyjadrujeme poďakovanie Ing. Petrovi Hanzelymu, ktorý sa rámci svojej záverečnej práce podieľal na riešení tejto problematiky.

Literatúra

1. Soille, P., Morphological Image Analysis. Springer-Verlag, 1999.
2. Girod, B.: Morphological Image Processing. Digital Image Processing, Stanford University, 2013. Dostupné online:
   https://web.stanford.edu/class/ee368/Handouts/Lectures/2014_Spring/Combined_Slides/7-Morphological-Image-Processing-Combined.pdf
3. Banon, G.J.F., Barrera, J., Ulisses Braga-Neto: Mathematical Morphology and its Applications to Signal and Image Processing. Proc. of the 8th International Symposium on Mathematical Morphology (ISMM’07), 2007.
4. Dougherty, E.R., Lotufo, R.A.: Hands-on Morphological Image Processing. SPIE Publications, 2003.
5. Sonka, M., Hlavac, V., Boyle, R.: Image Processing, Analysis and Machine Vision. CL Engineering, 2014.
6. Loce, R.P., Dougherty, E.R.: Using structuring-element libraries to design suboptimal morphological filters. Proc. SPIE, Image Algebra and Morphological Image Processing II Vol. 1568, pp. 233–246, 1991.
7. Liang, L., Phillips, I.T., Haralick, R.M.: Document Image Restoration Using Binary Morphological Filters.  Proceedings of SPIE – The International Society for Optical Engineering, May 1998.
8. Ronse, Ch., Najman, L., Decenciere, E.: Mathematical Morphology: 40 Years On. Springer, Netherlands, 2005.
9. Gladišová, I., Mihalík, J., Petráš, J.: Vnútrosnímková segmentácia obrazu. In: www.posterus.sk, portal pre odborné publikovanie, roč.8, č.2, s.1-18, 2015.

---

Spoluautor článku: Ján Mihalík. Laboratórium číslicového spracovania obrazov a videokomunikácií, Katedra elektroniky a multimediálnych telekomunikácií, Fakulta elektrotechniky a informatiky, Technická univerzita v Košiciach.