Prvkom prirodzenej inteligencie človeka je schopnosť učiť sa a využívať svoje znalosti spolu s intuíciou pri rozhodovaní. Cieľom umelej inteligencie je napodobniť tieto prvky, pričom prostriedky k dosiahnutiu tohto zámeru sú rôzne. Špecifickými sú napríklad evolučné algoritmy, ktoré si berú príklad z Darwinovej evolučnej teórie. Tá je založená na myšlienke, že v prírode dochádza k prirodzenému výberu, na základe ktorého prežijú len tí najschopnejší jedinci.

Vhodnou interpretáciou tejto myšlienky sa vytvorila sada nástrojov, ktoré sa využívajú v oblasti optimalizácie [1, 2]. Iným príkladom sú umelé neurónové siete, ktoré si za základ berú biologickú neurónovú sieť. Vedia napodobniť činnosť mozgu, ktorá je založená na procese učenia a neskoršieho využívania týchto znalostí. Vďaka tejto schopnosti je ich využitie v rôznych oblastiach viac než prínosom [3, 4].

Cieľom tejto práce je ukázať schopnosť umelej inteligencie riešiť dané problémy. Na reálnom systéme, teplovzdušnej sústave, sa pomocou neurónovej siete vytvorí dynamický model. Ten bude slúžiť k testovaniu evolučných algoritmov, ktoré sa budú snažiť nastaviť parametre PID regulátoru. Kvalita riadenia takto nastaveného regulátoru sa potom porovná s regulátorom, ktorého parametre boli nastavené klasickou metódou.

1. Popis riadenej sústavy

Riadenou sústavou je teplovzdušný model (obr. 1), ktorý je tvorený zdrojom tepla – žiarovkou, ktorá je umiestnená v krytom tuneli. V tuneli je nasávaný alebo vytláčaný vzduch pomocou 2 ventilátorov – hlavného a vedľajšieho (poruchového). Vedľajší ventilátor má opačný smer prúdenia vzduchu ako hlavný ventilátor. Posledným prvkom sústavy je vrtuľový prietokomer.

Obr. 1: Teplovzdušný model TVM

Sústavu môžeme ovládať pomocou dvoch akčných členov. Jedným z nich je zdroj tepla (žiarovka), ktorá je napájaná z nastaviteľného napäťového zdroja. Pre meranie teploty vzduchu v blízkosti žiarovky sú použité 3 termistorové snímače, ktoré sú rozmiestnené v rozsahu 0-5 mm od banky žiarovky. Druhým akčným členom je hlavný ventilátor, u ktorého môžeme nastavovať otáčky. Oba tieto vstupy je možné ovládať hodnotami v rozsahu 0-10 V.

Okrem spomínaných sa tu nachádza ešte ďalší akčný člen – poruchový ventilátor, ktorý je ovládaný pomocou diskrétneho výstupu, čiže nadobúda len dva stavy – 0 alebo 1, respektíve zapnutý/vypnutý. Keďže okrem snímania teploty pomocou termistorov môžeme merať aj prietok vzduchu v tuneli pomocou vrtuľového prietokomeru, model nám umožňuje realizovať jednorozmerné aj mnohorozmerné regulačné úlohy.

1.1 Chovanie sústavy v prechodových stavoch

V tejto kapitole som merala časovú odozvu na stupňovitý signál, ktorým bolo napätie na žiarovke. Napätie na ventilátore bolo konštantné po celú dobu merania. Výstupom boli hodnoty merané termistorom, nachádzajúcim sa 5 mm od banky žiarovky. Grafické znázornenie je zobrazené na obr. 2.

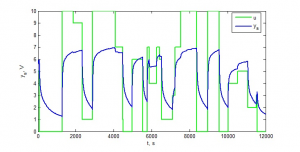
Obr. 2: Chovanie sústavy v prechodových stavoch

2. Experimentálna identifikácia pomocou umelej neurónovej siete

Niekedy môže byť použitie klasických matematicko-fyzikálných metód a metód experimentálnej identifikácie nepraktické, či už z dôvodu prílišnej zložitosti navrhnutého systému alebo neúplnej znalosti všetkých fyzikálno-chemických konštánt. Vtedy nastupujú alternatívne metódy tvorby modelov, medzi ktoré patrí aj využitie umelých neurónových sietí [5, 6]. Aby mohol byť model navrhnutý pomocou umelých neurónových sietí úspešne, je potrebné splniť určité základné podmienky. Je nutné zvoliť správnu topológiu siete, čo zahŕňa určenie počtu vrstiev siete, definovanie počtu neurónov v jednotlivých vrstvách a výber aktivačných funkcií. Parametre siete – váhy a prahy – sa určujú počas trénovania siete pomocou rôznych metód (Levenberg-Marquardt, Backpropagation, a i.).

Kým sa pristúpi k samotnému učeniu neurónovej siete je potrebné získať a upraviť vstupné a výstupné trénovacie dáta tak, aby boli vhodné pre proces učenia. Trénovacie dáta sa získavajú buď nameraním hodnôt vstupných a výstupných veličín sústavy, alebo to môžu byť výsledky matematických rovníc, ktoré danú sústavu popisujú. Pre určenie kvality siete sa po natrénovaní používajú testovacie dáta. Sieť je možné trénovať off-line, kedy sa zostaví kompletne celá množina trénovacích dát alebo on-line, kedy sa po získaní príslušného vzoru tento okamžite použije pre trénovanie. Je potrebné nastaviť aj dĺžku trénovania siete (počet trénovacích epoch), prípadne iné ukončovacie podmienky – dosiahnutá požadovaná hodnoty chyby E (odchýlka medzi výstupom z reálnej sústavy a neurónovým modelom), prípadne keď sa hodnota chyby nezlepšuje.

2.1 Tvorba dynamického neurónového modelu

Namerané dáta z kapitoly 1.1 sa použili ako základ pre tvorbu dynamického modelu sústavy. Model sústavy býva najčastejšie realizovaný v diskrétnom stave. Chovanie nelineárnej SISO dynamickej sústavy môžeme opísať diferenčnou rovnicou v tvare:

(1)

kde m a n je počet minulých hodnôt výstupov a vstupov, ktoré ovplyvňujú aktuálny vstup zo sústavy. Schéma sústavy je zobrazená na obr. 3.

Obr. 3: Schéma dynamickej nelineárnej SISO sústavy

Pri tvorbe dynamického neurónového modelu je potrebné najprv zvoliť rád sústavy. Môže sa postupovať dvoma smermi – začať s vyšším rádom a postupne ho znižovať alebo začať s najnižším rádom a ten postupne zvyšovať. Zvolila som druhý postup a nastavila m=n=1, čiže som pracovala s prvým rádom sústavy. Diferenčná rovnica teda nadobudla stav:

(2)

Namerané dáta z prechodovej charakteristiky bolo nutné zoradiť tak, aby boli vhodné pre učenie neurónovej siete. Zoradenie trénovacích dát je uvedené v tab. 1.

Tab. 1: Trénovacie dáta

k	Vstupné vzory		Výstupný vzor
	ys(k-1)	u(k-1)	ys(k)
1	y(0)	u(0)	y(1)
2	y(1)	u(1)	y(2)
…	…	…	…
N-1	y(N-2)	u(N-2)	y(N-1)
N	y(N-1)	u(N-1)	y(N)

Zvolila som neurónovú sieť s topológiou 2-10-1, čiže sieť obsahovala 2 vstupné neuróny, 10 neurónov v skrytej vrstve a 1 výstupný neurón. Aktivačné funkcie skrytých neurónov boli tansig – hyperbolický tangens a aktivačná funkcia výstupného neurónu bola purelin – lineárna funkcia. Učenie siete prebiehalo podľa algoritmu Levenberga-Marquardta. Keďže dáta boli namerané vopred, trénovanie neurónovej siete prebiehalo off-line. Základná schéma tohto typu trénovania je na obr. 4.

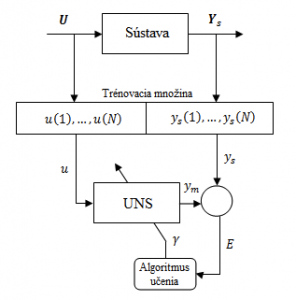
Obr. 4: Základná schéma off-line trénovania

Suma štvorcových odchýlok medzi výstupmi zo sústavy a výstupmi zo siete bola 586,53. Grafické znázornenie toho ako sieť aproximovala dáta je zobrazené na obr. 5

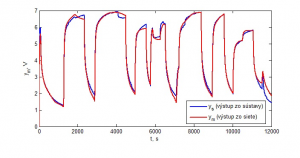
Obr. 5: Porovnanie výstupov zo sústavy s výstupmi z UNS (štruktúra 2-10-1)

Ďalším krokom bolo zvýšenie rádu rovnice sústavy o 1 stupeň. Parametre m a n sa teda rovnali 2. Diferenčná rovnica vyzerala nasledovne:

(3)

Keďže sieť zmenila počet vstupných vektorov z  2 na 4 a nadobudla štruktúru 4-10-1, bolo opäť nutné upraviť trénovacie dáta do takého stavu aby tejto štruktúre odpovedali. Tvar trénovacích dát je zobrazený v tab. 2.

Tab. 2: Trénovacie dáta

k	Vstupné vzory				Výstupný vzor
	ys(k-1)	ys(k-2)	u(k-1)	u(k-2)	ys(k)
2	y(1)	y(0)	u(1)	u(0)	y(2)
3	y(2)	y(1)	u(2)	u(1)	y(3)
…	…	…	…	…	…
N-1	y(N-2)	y(N-3)	u(N-2)	u(N-3)	y(N-1)
N	y(N-1)	y(N-2)	u(N-1)	u(N-2)	y(N)

Ostatné parametre – učiaci algoritmus, aktivačné funkcie, ostali rovnaké ako v prvom pokuse. Po natrénovaní siete bola štvorcová odchýlka medzi výstupmi zo sústavy a výstupmi zo siete 1789,14. Grafické znázornenie porovnanie výstupov je zobrazené na obr. 6.

Obr. 6: Porovnanie výstupov zo sústavy s výstupmi z UNS (štruktúra 4-10-1)

Zvýšenie rádu sústavy teda spôsobilo, že sieť aproximovala dáta horšie než pri nižšom ráde. Použitie vyššieho rádu je teda zbytočne zložité a neprinieslo lepšie riešenie. Vrátila som sa teda k nastavení parametrov m=n=1 a skúšala som meniť počet neurónov v skrytej vrstve. Cieľom bolo nájsť ešte lepšie riešenie než pri 10-tich neurónoch. Pokúsila som sa ten počet zvýšiť o 1, sieť teda nadobudla štruktúry 2-11-1. Výsledná chyba E nadobudla pri tejto štruktúre siete hodnoty 609,07, teda zvýšenie počtu neurónov neprinieslo zlepšenie.

Pokúsila som sa teda znížiť počet neurónov v skrytej vrstve o 1. Sieť typu 2-9-1 však tiež nezlepšila chybu, jej hodnota bola 645,97. Grafické znázornenie odchýlky oboch sietí je na obr. 7 (sieť typu 2-11-1) a obr. 8 (sieť typu 2-9-1).

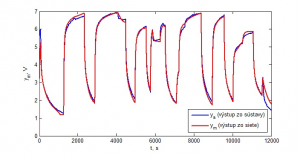
Obr. 7: Porovnanie výstupov zo sústavy s výstupmi z UNS (štruktúra 2-11-1)

Obr. 8: Porovnanie výstupov zo sústavy s výstupmi z UNS (štruktúra 2-9-1)

3. Nastavovanie parametrov PID regulátoru

Cieľom tohto experimentu bolo porovnať kvalitu nastavenia parametrov PID regulátoru pomocou klasických techník a pomocou evolučných algoritmov – genetického algoritmu (GA) a diferenciálnej evolúcie (DE).

3.1 Nastavenie parametrov PID regulátoru pomocou genetických algoritmov

K tejto práci som využila dynamický neurónový model, ktorý som vytvorila v predchádzajúcej úlohe. Bol tvorený doprednou neurónovou sieťou so štruktúrou 2-10-1, ktorá vykazovala najmenšiu odchýlku pri aproximácii dát zo sústavy. Parametre genetického algoritmu boli nastavené nasledovne: populáciu tvorilo 20 jedincov, pričom každý z nich bol zakódovaný binárnym kódovaním. Každý jedinec niesol informáciu parametrov P, I a D. Prehľadávaný priestor jednotlivých parametrov regulátoru bol v intervale <0,15>.

Priebeh ohodnocovania jedincov bol: Pri počte krokov N=1000 a s periódou vzorkovania T=1s sa nastavil požadovaný priebeh výstupnej veličiny. V prvej polovici bol požadovaný výstup nastavený na hodnotu 3 a v druhej polovici sa navýšil na hodnotu 6. Vstupný akčný zásah u bol nulový a aktuálny výstup y_m sa rovnal 1. Cieľom bolo, aby diskrétny PID regulátor riadil sústavu tvorenú dynamickým neurónovým modelom tak, aby bola suma štvorcových odchýlok medzi žiadanou hodnotou a výstupnou veličinou čo najmenšia. Akčný zásah diskrétneho PID regulátoru sa v k-tom kroku vypočítal nasledovne:

(4)

pričom parametre q₀, q₁, q₂ sa vypočítali:

(5)

(6)

(7)

kde: T – interval vzorkovania, r₀ – proporcionálna konštanta regulátoru, r₁ – integračná konštanta regulátoru, r₂ – derivačná konštanta regulátoru, T_i – integračná časová konštanta, T_d – derivačná časová konštanta.

Genetické algoritmy nachádzali podobné riešenie aj pri rôznych nastavení parametrov kríženia a mutácie. Pri nájdených parametrov PID regulátoru: r₀ =14,01, T_i=8,87 a T_d=0,5 bola odchýlka E rovná 146,2. Grafické zobrazenie priebehu regulácie neurónového modelu s požadovanou hodnotou w, akčným zásahom u a výstupnou y_m veličinou je zobrazené na obr. 9 a 10.

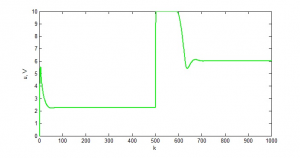
Obr. 9: Priebeh akčnej veličiny

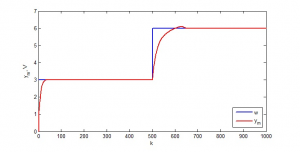
Obr. 10: Priebeh regulácie neurónového modelu pomocou diskrétneho PID regulátoru

Nastavenie parametrov PID regulátoru bolo následne vyskúšané na teplovzdušnej sústave. Ten sa snažil uregulovať výstup podľa žiadanej hodnoty. Jej priebeh bol zmenený kvôli všeobecnejšej validácii. Chybová odchýlka medzi žiadaným a reálnym výstupom zo sústavy bola E=141,04. Priebeh regulačného pochodu je zobrazený na obr. 11 a 12.

Obr. 11: Priebeh akčnej veličiny

Obr. 12: Regulačný pochod sústavy pri nastavení parametrov PID pomocou GA

3.2 Nastavenie parametrov PID regulátoru pomocou diferenciálnej evolúcie

Experiment s nastavením parametrov PID regulátoru som opakovala, tentokrát s použitím diferenciálnej evolúcie. Nastavenie parametrov – počtu epoch, veľkosti populácie prehľadávaného priestoru a funkciu fitness som ponechala rovnaké ako u genetických algoritmov. Prah kríženia som nastavila na 0,8 a parameter mutácie na 0,7. Algoritmus diferenciálnej evolúcie nachádzal podobné riešenia ako genetické algoritmy. Pre nájdené parametre regulátoru r₀=12,53, T_i=6,04 a T_d=0,11 bola chybová odchýlka E=145,51. Priebeh akčnej veličiny a regulačného pochodu neurónového modelu je zobrazený na obr. 13 a 14.

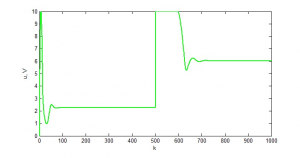
Obr. 13: Priebeh akčnej veličiny

Obr. 14: Priebeh regulácie neurónového modelu pomocou diskrétneho PID regulátoru

Nastavenie parametrov PID regulátoru bolo následne opäť vyskúšané na teplovzdušnej sústave. Chybová odchýlka medzi žiadaným a reálnym výstupom zo sústavy bola E=135,89, čiže o niečo lepšia než v prechádzajúcom prípade u genetického algoritmu. Priebeh akčnej veličiny a regulačného pochodu je zobrazený na obr. 15 a 16.

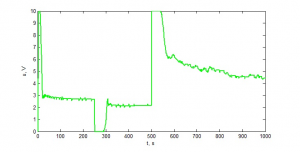
Obr. 15: Priebeh akčnej veličiny

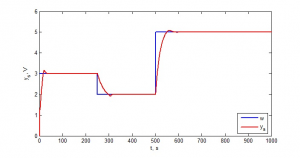
Obr. 16: Regulačný pochod sústavy pri nastavení parametrov PID pomocou DE

3.3 Nastavenie parametrov PID regulátora pomocou Kuhnovej metódy

Posledný pokus nastavenia parametrov PID regulátoru bol vykonaný klasickým spôsobom – Kuhnovou metódou [8]. Parametre sa určili z prechodovej charakteristiky, ktorá bola meraná s konštantným napätím na žiarovke 10 V a konštantným napätím na ventilátore 0 V. Parametre PID nájdené touto metódou sa prevzali z [9]: r₀=4,35, T_i=19,8 a T_d=5,01. Výsledný priebeh akčnej veličiny a regulačného pochodu je zobrazený na obr. 17 a 18.

Obr. 17: Priebeh akčnej veličiny

Obr. 18: Regulačný pochod sústavy pri nastavení parametrov PID pomocou Kuhnovej metódy

3.4 Zhodnotenie

V tejto časti práce som porovnávala nastavenie parametrov PID regulátoru klasickou metódou a pomocou evolučných algoritmov. Nastavenia parametrov evolučnými algoritmami bolo vykonávané na dynamickom neurónovom modeli sústavy. Výsledné hodnoty som uviedla spolu s grafmi. Odchýlka E pri nastavení parametrov pomocou genetických algoritmov bola 145,51. Pri diferenciálnej evolúcii sa hodnota znížila na E=135,89. Klasická metóda bola vykonávaná pomocou Kuhnovej metódy. Výsledná chyba E bola 216,02. Výsledkom tohto experimentu teda je, že použitie alternatívnych metód nastavovania parametrov PID regulátoru malo za výsledok lepšiu reguláciu sústavy.

4. Záver

Klasické metódy sú v oblastiach experimentálnej identifikácie a riadenia systémov zažité dlhodobým používaním. Táto práca poukazuje na možnosť nahradenia týchto metód inými, ktoré k svojej činnosti využívajú prvky umelej inteligencie. Pre testovanie kvality regulácie bol použitý reálny systém – teplovzdušná sústava. Namerané dáta z chovania tejto sústavy v prechodových stavoch boli použité ako základ pre vytvorenie dynamického neurónového modelu. Na ňom boli pomocou genetického algoritmu a diferenciálnej evolúcie hľadané optimálne parametre PID regulátoru. Nájdené parametre boli následne aplikované na reálnu sústavu.

Výsledky použitia oboch algoritmov boli porovnané s klasickou Kuhnovou metódou. Bolo zistené, že moderné metódy sú schopné v niektorých prípadoch tie klasické nielen nahradiť, ale prinášajú aj výhody napríklad v podobe kvalitnejšej regulácie.

Zoznam použitej literatúry

1. HAYKIN, S.: Neural Networks. Prentice Hall, New Jersey, 1999. 845 s.
2. TUČKOVÁ, J.: Úvod do teorie a aplikací umělých neuronových sítí. ČVUT, Praha, 2005. 103s.
3. HYNEK, J.: Genetické algoritmy a genetické programování. Grada, Praha, 2008. 182 s.
4. MAŘÍK, V., ŠTĚPÁNKOVÁ, O., LAŽANSKÝ, J.: Umělá inteligence (4). Academia, Praha, 2003. 479 s.
5. TAUFER, I.; DRÁBEK, O.; SEIDL, P.: Umělé neuronové sítě – teorie a aplikace (7). CHEMagazín, 3 (XVII), 2007, s. 2–7.
6. TAUFER, I.; DRÁBEK, O.; SEIDL, P.: Umělé neuronové sítě – teorie a aplikace (8). CHEMagazín, 4 (XVII), 2007, s. 28–30.
7. HLAVA, J.: Prostředky automatického řízení II. ČVUT, Praha, 2000. 162 s.
8. CHOVANCOVÁ, Veronika.: Řízení tepelné soustavy [Diplomová práca]. Univerzita Pardubice, Pardubice, 2008. 67 s.

---

Spoluautorom článku je Ing. Petr Doležel, Katedra řízení procesů, Fakulta elektrotechniky a informatiky, Univerzita Pardubice