Článok pojednáva o teoretickej podstate modelov, ktoré možno využívať pri riešení náročných úloh optimalizácie dynamických systémov – procesov. Uvedené poznatky a formulácie sa týkajú problematiky prijímania rozhodnutí najmä pri projektovaní výrobných systémov v diskrétnej strojárskej výrobe, pri rozvrhovaní a riadení výroby, v rámci zabezpečovania optimálnej prevádzky výrobných, dopravných, manipulačných, logistických a iných technických systémov. Podrobnejšie je opísaná podstata optimalizačného modelu, simulačného modelu, ako ak tzv. metamodelov.

Za samozrejmosť sa považuje, že východiskom k riešeniu zložitých optimalizačných úloh je vytvorenie vhodného modelu, ktorý odráža vlastnosti modelovanej reality, dôležité z hľadiska sledovaných cieľov a prípadne poskytuje aj prostriedky a nástroje na hľadanie čo najlepších riešení. Modely bývajú vytvárané účelovo. Možno ich však vytvárať s využitím určitých prístupov, čím získa model určitý charakter. Pri vytváraní modelov – optimalizačných aj simulačných sa vo všeobecnosti využíva buď deskriptívny prístup, alebo normatívny (resp. preskriptívny) prístup.

Deskriptívny prístup spočíva vo vytvorení usporiadanej množiny poznatkov, charakterizujúcich štruktúru alebo správanie sa určitého systému za účelom poznania podstaty jeho fungovania [8]. Iná definícia hovorí, že deskriptívny prístup popisuje javy, procesy a systémy tak, ako v daný moment vyzerajú [9]. Je to teda opisný prístup. Modely vytvorené na základe tohto prístupu sú deskriptívnymi modelmi, ktoré môžu mať rôzny charakter.

Môžu byť vytvorené v podobe matematických rovníc alebo nerovností (napr. klasické modely operačnej analýzy), grafov, matíc alebo tabuliek, ale môžu mať aj formu slovného opisu. Na účely simulácie sú vytvárané klasické simulačné modely, čo sú v podstate účelovo vytvorené počítačové modely. Je zrejmé, že každý model je vytváraný na určitý účel a pri jeho vytváraní musí byť zohľadnený aj predpokladaný spôsob jeho následného použitia.

Normatívny prístup vychádza z predpokladu, že súčasťou modelu je návod na hľadanie optimálnych alebo „čo najlepších“ riešení. Normatívny prístup analyzuje minulosť a predikuje budúcnosť. Podľa inej definície normatívny prístup popisuje javy, procesy a systémy tak, ako by mali vyzerať podľa platných noriem. Klasické analytické optimalizačné modely využívajú algoritmy a metódy na riešenie problémov alebo odporúčané postupy – niekedy viacetapové. V prípade simulačných modelov môže ísť tiež o odporúčania – väčšinou vychádzajúce zo skúseností a poznania podstaty riešených problémov, alebo algoritmy, ktoré môžu byť v prípade optimalizačných modulov priamo zabudované v simulačných softvérových produktoch.

V takomto prípade možno simulačný model považovať aj za model, ktorý využíva preskriptívny prístup, t.j. preskriptívny model [4]. Preskriptívny prístup (nariaďujúci) sa snaží nájsť nástroje, ktorými možno rozhodovanie zlepšiť. Tento prístup sa vyznačuje inkorporovaním poznatkov normatívneho prístupu, ale s prihliadnutím na kognitívne obmedzenia zistené prostredníctvom metód deskriptívneho prístupu [10].

Optimalizácia – optimalizačný model

Optimalizáciu možno definovať ako proces, ktorý smeruje k nachádzaniu riešení, ktoré sú „lepšie“ ako súčasný stav (už dosiahnutý alebo známy). Ide o proces zlepšovania, ktorého výsledkom môže, ale nemusí byť optimálne riešenie [2]. Problematikou optimalizácie sa zaoberá viacero teoretických disciplín. Medzi nimi má významné postavenie operačná analýza (resp. operačný výskum), ktorá je niekedy považovaná za vedeckú disciplínu, inokedy za súbor relatívne samostatných disciplín. Využíva deskriptívny model, ktorý možno všeobecne zapísať funkciou

(1)

alebo

(2)

Zápis (1) vyjadruje skutočnosť, že hodnota sledovanej výstupnej veličiny modelu y je funkciou kombinácie hodnôt vstupných veličín – nezávisle premenných x_i. Rozšírenie zápisu do podoby (2) možno použiť v prípade, že „kvalita“ modelovanej reality závisí od hodnôt viacerých sledovaných výstupných veličín – ide teda o viackriteriálnu optimalizáciu. Charakteristické a dôležité je (na rozdiel od simulačného modelu), že funkciu f možno zapísať ako matematickú funkciu a hodnotu výstupnej veličiny y, resp. veličín y_i, vypočítať.

Model možno zapísať aj ako zobrazenie, t. j. vzťah medzi množinami, pri ktorom je každému prvku (vzoru) prvej množiny priradený určitý prvok (jeho obraz) z druhej množiny:

(3)

Prvkami množiny X sú kombinácie hodnôt vstupných veličín modelu (x₁, x₂, …, x_n) a prvkami množiny Y sú kombinácie hodnôt výstupných veličín (y₁, y₂, …, y_m). Z definície zobrazenia vyplýva, že rôznym prvkom množiny X môže byť priradený ten istý prvok množiny Y, t. j. rovnaký cieľ možno dosiahnuť rôznymi spôsobmi. Model (1) sa stane optimalizačným až po tom, keď doňho zahrnieme cieľ, sledovaný v rámci optimalizácie, napr.:

(4)

a podmienky, ktoré musia spĺňať vstupné veličiny x_i , zadané intervalmi, v ktorých sa hodnoty týchto jednotlivých veličín môžu pohybovať, resp. matematickými rovnicami a nerovnicami, ktorým musia vyhovovať. Uvedený vzťah sa nazýva účelová funkcia. Podmienky, ktoré musia spĺňať vstupné veličiny sa napr. v prípade úloh lineárneho programovania nazývajú vlastné obmedzenia a podmienky nezápornosti.

V prípade viackriteriálnej optimalizácie treba odpovedať na otázku, aké hodnoty musia nadobúdať jednotlivé členy vektora Y , aby riešenie optimalizačnej úlohy mohlo byť považované za optimálne, resp. aká kombinácia hodnôt yi je optimálna, alebo „lepšia“ ako iná. Charakteristickou črtou väčšiny postupov operačnej analýzy, ktoré narábajú s modelmi uvedeného typu je, že optimálne alebo vyhovujúce riešenia sú hľadané analytickým riešením – výpočtom [4].

Simulácia – simulačný model

Podľa jednej z definícií – známej Dahlovej definície je simulácia výskumná metóda, ktorej podstata tkvie v tom, že skúmaný dynamický systém nahradíme jeho simulátorom a s ním potom vykonávame pokusy s cieľom získať informáciu o pôvodnom skúmanom systéme [5]. V literatúre existuje aj viac definícií simulačného modelu. Napr.:

Simulačný model je dynamický model, pre ktorý je príznačné, že v modelovanom systéme je poradie výskytu javov rovnaké ako v modelujúcom systéme. Simulačný model možno opísať ako usporiadanú šesticu <Z₁, Z₂, m, M, τ, R>, kde

Z₁ je modelovaný (simulovaný) systém, Z₂ – modelujúci (simulujúci) systém, m – prvková zložka modelu, M – atribútová zložka modelu, τ – časová zložka modelu, R – relačná zložka modelu.

Tradičný simulačný model je (z hľadiska uvedenej klasifikácie modelov) deskriptívnym modelom (nie preskriptívnym). To znamená, že poskytuje informáciu o tom, ako modelovaný systém pracuje v daných podmienkach, nie o tom, ako nastaviť podmienky, aby systém pracoval optimálne [4]. Simulátor je modelujúci systém v simulačnom modeli, definovaný na reálnom objekte. Na označenie simulátora sa však bežne používa aj pojem „simulačný model“ [3, 5, 6].

Keďže účelom používania simulačného modelu býva nájdenie optimálneho, alebo „čo najlepšieho“ riešenia, možno ho vyjadriť, podobne ako optimalizačný model – funkciou (5) resp. (6), alebo zobrazením (7).

(5)

alebo

(6)

(7)

Na označenie premenných, ktoré zodpovedajú nezávisle premenným optimalizačného modelu budeme teraz používať vhodnejšie označenie „vstupné parametre“ a na označenie veličín získavaných na výstupe simulačného experimentu označenie „sledované výstupné veličiny“ modelu.

Funkciu _f , na rozdiel od optimalizačných modelov, spomenutých v predchádzajúcej časti, nemožno zapísať ako matematickú funkciu. Je realizovaná cez simulačný experiment so simulačným modelom. Hodnoty sledovaných výstupných veličín nemožno vypočítať, ale sú získané na výstupe experimentu so simulačným modelom. V určitých prípadoch môžu byť získané ako výsledok následného výpočtu, do ktorého môžu vstupovať okrem aspoň jednej takejto výstupnej veličiny zo simulačného experimentu aj hodnoty vstupných parametrov modelu alebo rôzne konštanty.

Vstupné parametre majú často charakter náhodných veličín. Sú preto zadávané prostredníctvom teoretických alebo empirických rozdelení pravdepodobnosti a ich parametrov. Je zrejmé, že aj výstupné veličiny majú charakter náhodných veličín, čo treba zohľadniť pri ich interpretácii. Pri posudzovaní výsledkov simulačného experimentu býva niekedy zaujímavá nielen výsledná hodnota výstupnej veličiny (napr. priemerná dĺžka frontu), ale aj dynamika zmien hodnôt určitej veličiny počas simulačného behu (napr. časová závislosť dĺžky frontu) [4].

Optimalizácia založená na využití simulácie

Hľadanie optimálnych riešení spôsobmi, ktoré sú založené na využití modelu uvedeného v tejto časti, sú v literatúre označované napr. pojmami „simulation-based optimization“[7], alebo „optimization via simulation“[1]. Klasický simulačný model (5), resp. (6), býva využívaný v rámci postupov hľadania optimálnych alebo „čo najlepších“ riešení ako prostriedok na overovanie jednotlivých variantov v postupnosti krokov smerujúcich k optimu. Nemožno ho však považovať za optimalizačný v pravom zmysle slova, pretože v ňom nie je zahrnutý cieľ optimalizácie. Optimalizačným sa môže stať po doplnení o funkciu g :

(8)

ktorá sa podobne ako v prípade klasického optimalizačného modelu stane účelovou funkciou po doplnení o cieľ optimalizácie a podmienky, ktoré musia spĺňať vstupné parametre p_i ale niekedy aj výstupné veličiny  y_j. Táto účelová funkcia môže mať napr. tvar:

(9)

ale cieľom môže byť aj jej minimalizácia, alebo čo najväčšie priblíženie sa k určitej hodnote z_opt. Cieľom môže byť aj hľadanie takej kombinácie hodnôt parametrov modelu, ktorá vedie pri väčšom počte experimentov k čo najväčšej pravdepodobnosti, že hodnota z bude (nebude) menšia (väčšia) ako určitá zadaná hodnota z_lim [2].

Nie všetky p_i a y_j sa musia nachádzať v rovnici účelovej funkcie (niektoré sa môžu vyskytovať s koeficientom 0). Na to, aby mohol byť model považovaný za optimalizačný simulačný model, je však nevyhnutná prítomnosť aspoň jednej veličiny y_j. Funkciu g , na rozdiel od funkcie f v simulačnom modeli, možno (a dokonca treba) zapísať ako matematickú funkciu. Optimalizačný simulačný model, obsahujúci vzťahy (6) a (9) je použiteľný v rámci jednokriteriálnej optimalizácie napriek tomu, že obsahuje viac výstupných veličín y_j. Ich vplyv sa totiž prejaví v hodnote jednej vypočítanej veličiny – v hodnote účelovej funkcie z .

Je zrejmé, že všetky výstupné veličiny optimalizačného simulačného modelu sú veličinami, ktorých hodnota je vyčíslená po ukončení simulačného behu (napr. počet vyrobených výrobkov). Veličiny, ktorých hodnota sa počas simulačného behu mení (napr. dĺžka frontu) môže byť v účelovej funkcii prítomná len po vyhodnotení (napr. ako priemerná alebo maximálna dĺžka frontu počas simulačného behu).

Podstata a účel použitia metamodelov

Simulačné modely sa spravidla používajú na zistenie predpokladaného správania sa modelovanej reality. Väčšinou sa posudzujú alebo navzájom porovnávajú viaceré varianty, ktoré sa môžu navzájom odlišovať štruktúrou, alebo len hodnotami vstupných parametrov. Ak sa jednotlivé varianty navzájom odlišujú len hodnotami vstupných parametrov, alebo ich odlišnosti v štruktúre možno vyjadriť hodnotami vstupných parametrov, možno model transformácie vstupných parametrov na hodnotu výstupnej veličiny všeobecne vyjadriť funkčnou závislosťou (5), resp. (6). Cieľom experimentovania so simulačným modelom býva väčšinou porovnanie variantov simulačného modelu z hľadiska hodnoty sledovanej výstupnej veličiny (prípadne viacerých výstupných veličín).

Ak na posudzovanie systému používame simuláciu, hodnota výstupnej veličiny je získaná vykonaním simulačného experimentu, resp. ako výsledok štatistického spracovania výstupných veličín, získaných z postupnosti experimentov. Väčšinou má charakter náhodnej veličiny. Nemožno ju vypočítať, pretože ani uvedenú funkciu v prevažnej väčšine prípadov nemožno priamo matematicky sformulovať. Je však zrejmé, že matematické vyjadrenie uvedenej závislosti by mohlo slúžiť ako vhodný podklad na predikciu správania sa modelovaného objektu. To viedlo k úsiliu formulovať matematické zápisy závislostí vyjadrených touto funkciou, tzv. metamodely. Podkladom na vytvorenie metamodelu sú vykonané simulačné štúdie – postupnosti experimentov s variantmi simulačného modelu.

V najjednoduchšom prípade závislosť obsahuje len jeden relevantný vstupný parameter ( i = 1). Graficky možno takúto závislosť vyjadriť krivkou. Ak je zrejmé, že pôjde o lineárnu závislosť, stačí na sformulovanie závislosti vykonať simulačné experimenty s dvoma hodnotami parametrov. Získajú sa 2 body, ktorými možno preložiť priamku, resp. vypočítať koeficienty a a b v rovnici priamky .

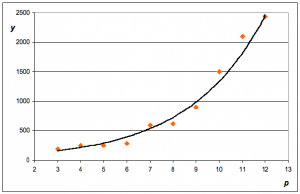
Ďalšou možnosťou je vytvorenie takéhoto modelu na základe postupnosti experimentov s viacerými hodnotami parametra – použitím metódy najmenších štvorcov (obr. 1). V reálnych podmienkach však je otázne, do akej miery je predpoklad lineárnosti opodstatnený. Ak použijeme druhú z uvedených metód, možno na základe grafického znázornenia výsledkov jednotlivých experimentov subjektívne odhadnúť, či by mohlo ísť o lineárnu závislosť. Či je takýto odhad postačujúci, záleží od účelu použitia vytváraného metamodelu. V každom prípade, ak bude model použitý na predikciu správania sa reálneho objektu, vhodnejšie je vyjadriť ho v tvare , kde slúži na všeobecné vyjadrenie stochastických vplyvov pri vytváraní metamodelu. Ide o klasický lineárny regresný model.

Obr. 1: Priamka preložená metódou najmenších štvorcov

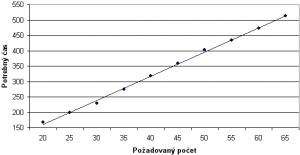
Pravdivosť a dôveryhodnosť metamodelu možno zvýšiť, ak pri jeho vytváraní bude zohľadnený stochastický charakter všetkých jeho parametrov. Na obr. 2 je príklad grafického zobrazenia takéhoto metamodelu. Ide o príklad závislosti času, potrebného na obslúženie požadovaného počtu požiadaviek od požadovaného počtu požiadaviek s pravdepodobnosťou 95%. Pri určovaní šírky pásu boli využité vypočítané hranice predikčných intervalov [2].

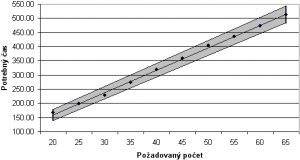
Obr. 2: Metamodel na predikciu správania sa systému so zvolenou pravdepodobnosťou.

V literatúre sú analyzované aj iné modely, ktoré možno považovať za lineárne [1, 7] aj nelineárne (obr. 3). Na názorné zobrazenie niektorých z nich možno použiť trojrozmerné zobrazenie (obr. 4), alebo zobrazenie pomocou vrstevníc (obr. 5).

Obr. 3: Nelineárny metamodel

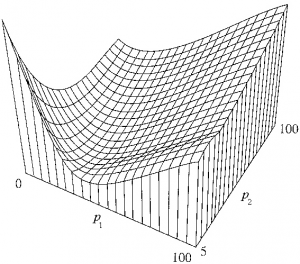
Obr. 4: Príklad trojrozmerného zobrazenia metamodelu [7]

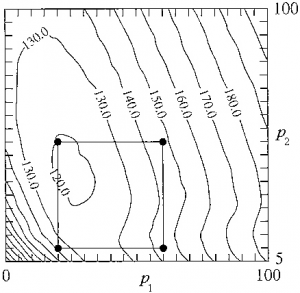
Obr. 5: Príklad zobrazenia metamodelu pomocou vrstevníc [7]

Článok bol vytvorený v rámci riešenia výskumnej úlohy KEGA 3/7307/09 Návrh metodiky využívania nástrojov 3D modelovania a virtuálnej reality v podmienkach výučby v špeciálnych laboratóriách.

Použitá literatúra:

1. Banks, J., Carson II, J.S., Nelson, B.L., Nicol, D.M.: Discrete-Event System Simulation. Pearson Prentice Hall 2005. 608 s., ISBN 0-13-129342-7
2. Jerz, V.: Simulácia a optimalizácia v procese prijímania rozhodnutí. Habilitačná práca. Bratislava: SjF STU 2009
3. Jerz, V.: Simulácia systémov. Bratislava: ES STU 1991, ISBN 80-227-0458-X
4. Jerz, V.: Teoretické úvahy o podstate simulačného optimalizačného modelu. In.: Zborník z 13. ročníka medzinárodnej konferencie Witness 2010. Brno: Humusoft & VUT Brno 2009, s. 25-29, ISBN 978-80-214-4107-1
5. Jerz, V., Tolnay, M.: Simulácia diskrétnych systémov. Bratislava: Vydavateľstvo STU 2006. 162 s., ISBN 80-227-2384-3
6. Kindler, E.: Simulační programovací jazyky. Praha: SNTL, 1980.
7. Law, A.M.: Simulation Modeling and Analysis. McGraw-Hill Companies 2007. 768 s., ISBN-13 978-0-07-298843-7, ISBN-10 0-07-298843-6
8. Pinka, D., Szabó, Ľ.: Podnikateľské rozhodovanie. Bratislava: ES EU 1993
9. http://referaty.atlas.sk/odborne-humanitne/ekonomia/9840/?page=4 (3.2.2010)
10. http://ffweb.ff.upjs.sk/vyuka//Katedra%20psychologie/Jozef%20Bavolar/Psychologia%20rozhodovania/1%20Definicie%20zakladnych%20pojmov,%20hlavne%20pristupy/1.%20Defin%edcie%20z%e1kladn%fdch%20pojmov%20psychol%f3gie%20rozhodovania,%20hlavn%e9%20pr%edstupy,%20oblasti%20z%e1ujmu%20psychologick%e9ho%20sk%famania.pdf (3.2.2010)

---

Ústav výrobných systémov, environmentálnej techniky a manažmentu kvality
Strojnícka fakulta STU Bratislava